Control of Augmented Minimal Model for Glucose Insulin Pump
Muhammad Farman1* and Muhammad Umer Saleem2
1 Department of Mathematics and statistics, University of Lahore, Pakistan
2 Department of Mathematics, University of Education, Pakistan
Submission: June 20, 2018; Published: August 24, 2018
*Corresponding author: Muhammad Farman, Department of Mathematics and statistics, University of Lahore, Pakistan.
How to cite this article: Md Farman, Md Umer S. Control of Augmented Minimal Model for Glucose Insulin Pump. Curre Res Diabetes & Obes J. 2018; 8(4): 555742. DOI: 10.19080/CRDOJ.2018.08.555742.
Abstract
A control system can only be used in the form of closed-loop control to stabilize the system. The concept of controllability and observability for the linearized control system of human glucose insulin systems is used so that we can have a feedback control. We have treated an existing model i.e. Augmented minimal model of glucose kinetics for type 1 diabetes. We checked the stability analysis by using the Lyapunov theorem of the model, controllability and observability of the model for close loop design for this purpose. Numerical simulation is discussed of controllability and observability at equilibrium point and di event conditions.
Keywords: Controllability; Observability; Arterial pancreas; Lyapunov function; Stability analysis
Introduction
Controllability and Observability are major questions in the analysis of a system before Xing on the best control approach to be practical, or whether it is even possible to control or steady the system. Controllability is connected to the opportunity of forcing the system into a particular state by using a suitable control signal. If a state is not convenient, then no signal will ever be capable to control the state. Observability in its place is associated to the possibility of examining, through output capacity, the state of a system. If a state is not visible, the controller will never be able to establish the behavior of an unobservable state and hence cannot use it to calm the system. A nil step in the control system propose problem is, of course, to understand the mathematical model of the controller by a genuine physical device, often in the form of appropriate hardware and software, and to intersect this device with the to be controlled physical system [1-3].
Diabetes is a worldwide problem of the day. It is a group of diseases enclosed in a single term diabetes mellitus. It is caused by disorder of the pancreatic endocrine hormonal secretions in the human body. When blood glucose level is too much increased in the body then a chronic condition known as diabetes mellitus is diagnosed in the body. Pancreas and its secretions insulin and glucagon are responsible to regulate the sugar level in our body. Normally when blood glucose concentration is too high in the body then insulin is secreted which stimulates the cells to absorb the extra glucose for the energy or fuel, that they need. Similarly, on the other hand when blood glucose level is getting very low then stimulation will occur in pancreas to secrete glucagon to increase the blood glucose level up to normal level to regulate the system in the body. On the basis of deficiency and insufficiency diabetes is of two types called type 1 and type 2. Nowadays, type 1 diabetic patients have to control their blood glucose level by periodically monitoring their blood glucose levels. Generally, blood glucose concentration is measured by a chemically active test strip, 3 to 8 times a day. Based on external and internal disturbances, which include physical activity and psychological stress, and based on measured glucose, the patient has to determine the required amount of insulin and inject it by a pen or pump. In essence, the patient is the controller as well as the metabolic system, which has to be controlled. Due to discrete sampling rate and poor knowledge of system disturbances, the manual insulin therapy can usually not keep the blood glucose concentration within the desired physiological range of 70 to 180mg/dl [4-6].
To improve insulin therapy, since the 1970’s, various research groups around the world have invested significant e orts to develop an automated closed-loop blood glucose system which is better known as artificial pancreas. The aim is to couple a sensor which continuously monitors the blood glucose concentration with a continuously injecting insulin pump based on a control algorithm to regulate the blood glucose within a tolerable range [5]. Until today, the continuously injecting insulin pump is the sole commercially available device for automated insulin therapy. A reliable blood glucose sensing device is still being sought. Finally, the application of published blood glucose control algorithms is limited to clinical studies under controlled conditions, which do not represent most normal life situations [6,7]. The ability to simulate the glucose insulin system in normal life conditions can be very useful in diabetes research. Several simulation models have been proposed in the literature that proved to be useful in tackling various aspects of pathophysiology of diabetes. Recently, a new meal simulation model has been proposed [8]. Artificial pancreas is a innovation to preserve the typical blood glucose level in diabetes with a substitute endocrine work to pancreas. The task is lacking to oversee physically the blood glucose level with alone that is why the current treatment of affront substitution (Artificial Pancreas) is appreciated for its life sparing capability. This treatment can help in the hypoglycemia state by catapulting more affront by the affront pump but in case of hypoglycemia state this treatment will not work. Hypoglycemia leads to neuroglycopenia and impacts can run from gentle dysphoria to more serious issues such as seizures, obviousness, harmful for brain cells and death.
Often, the behavior of a system is studied and described mathematically. This description is called a model, and it should reproduce the outputs of a system, based on the inputs, as accurately as possible. However, quite often, models are not capable of capturing the whole behavior of a system, either because it is too complex, or disturbances are too important. A system is called static if its outputs at a given time are influenced by the inputs at that time, only. In a dynamical system, however, the outputs are determined by current and past inputs. A controller is used to adjust a systems inputs, in order to obtain desired outputs. This system is called controlled system. A controller itself can be considered as a system, whose output is the controlled systems input. If the controlled inputs depend directly on the controlled systems outputs, then the controller is called a closed-loop controller, otherwise it is called an open-loop controller. The output value that a closedloop control algorithm is intended to reach is called a set point [9].
Since in recent years fractional calculus has attracted great attentions from researchers and different aspects of the said subject are under consideration for research. This is due to the fact that fractional derivative is important tool to explain the dynamical behavior of various physical systems. The strength of these differential operator is their nonlocal characteristics which does not exist in the integer order differential operators. The distinguished features of fractional differential equations are that it outlines memory and transmitted properties of numerous mathematical models [14].
In this paper we find the equilibrium points of the model and check its stability analysis of the models by using Lyapunov equation. If the equilibrium point lies in the feasible region then by using the Jacobian, convert the nonlinear system of equation into linearized system and discussed the controllability and observability of the linearized system to design the close loop for automatic artificial pancreas. We treated the glucose insulin model for healthy and type-1 diabetes and numerical simulations are carried out to support the analytical results.
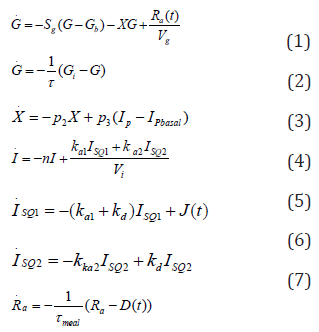

In these equations, t is the independent model variable time, G(t) is the plasma glucose concentration (mg/dL), I(t) is the plasma insulin level (U/mL) and X(t) is the interstitial insulin activity. Gb is the basal plasma glucose concentration (mg/dL) and is the basal plasma insulin concentration (U/mL). Basal plasma concentrations of glucose and insulin are typically measured before administration of glucose (or sometimes 180 minutes after). and are the subcutaneous insulin transport after injection (J), is the glucose rate appearance from a meal D (Table 1). These are unknown parameters in this model: Sg, Vg, p2, p3, ka1, ka2, kd and n [8,10]. Model after substitution parameter value becomes
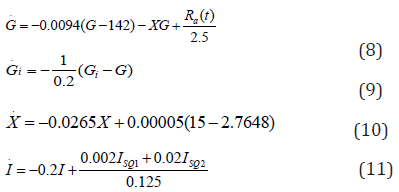
Put left hand side of the system (3:8 3:14) equal to zero and get the Equilibrium point of the model is
(G; Gi; X; I; ISQ1; ISQ2; Ra) = (3091.85; 3091.85; 0.023085; 2.97056; 37.132; 0; 247.76)
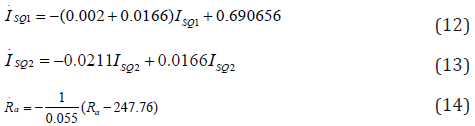
Hence, the linearized model according to the equilibrium point is
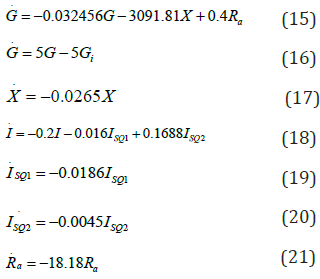
Theorem 1: The linear where A continuous and bounded for, is uniformly asymptotically stable if and only if given a positive definite real matrix A, there exists a symmetric positive definite real matrix P, which satisfies
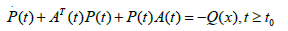
The linear time invariant system . x = Ax(t) the corresponding equation to be used as AT P + PA+Q = 0 this is called Lyapunov equation [11-13]. Here
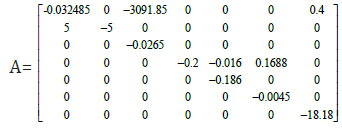
and substitute 6*6 Q = I in AT P + PA+Q = 0 , the Lyapunov equation has symmetric positive-definite solution P, then the eigen values of A are
(−5.0000,−0.3285,−0.0285,0.2000,−0.0186,−0.0045,−18.18000)
Has negative real parts, so the system . x = Ax(t) is asymptotically and uniformly stable
Linear Control System
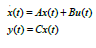
Consider the linear system
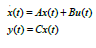
In this case we have
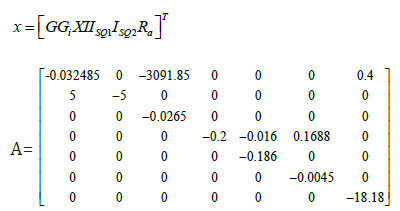
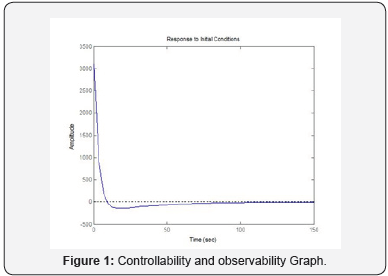
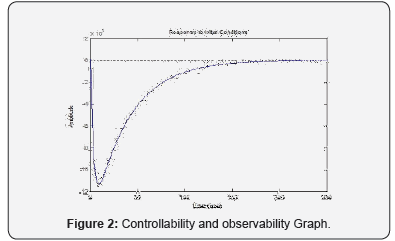
If we consider the glucose concentration in plasma is the only measured output and the insulin concentration in plasma is only input, then B = [0 0 1 0 0 0]T and C = [1 0 0 0 0 0 0]. The control- lability matrix is R = [B AB A2B …. A6B] and its rank is 1. So, the system is not controllable. The observability matrix is O = [C; CA; CA2; CA3; …..CA6]T and its rank is 3. So, the system is not observable. At equilibrium point (3091:85; 3091:85; 0:023085; 2:97056; 37:132; 0; 247:76) and at different initial conditions like (100; 0; 11:01; 0; 0; 0; 0), (100; 0; 11:01; 11:01; 11:01; 0; 0), (110; 0; 15:01; 0; 0; 0; 0), (130; 0; 20:01; 0; 0; 0; 0) the controllability and observability of the graph is approaches to zero, so system not work like close loop for feedback design are shown in (Figure 1 & 2).
Conclusion
For the purpose automatic artificial pancreas in the glucose regulatory system we discuss model Augmented Minimal Model of Glucose Kinetics and reduced meal model which had a simple but comprehensive model. For this purpose, we check the controllability and observability of the system. In this model, we consider that only measured output is concentration of glucose in plasma that we can measured easily. The system is not controllable neither observable. The controllability and observability of the graph is approaches to zero, so system not work like close loop for feedback design.
References
- Coron JM (2007) Control and nonlinearity, American Mathematical society 136.
- Farman M, Saleem MU, Ahmad MO (2017) An Approach for Arti cial Pancreas to Control the Type-1 Diabetes Mellitus, J Appl Environ Biol Scie 11(5): 93-102.
- Morris KA (2001) Introduction to Feedback Control. Academic Press, San Diego, USA.
- Saleem MU, Farman M, Ahmad MO, Rizwan (2017) A Control of Arti cial Pancreas in Human, Chines journal of Physics 55(6): 2273-2282.
- Lunze K, Brendel MD, Leonhardt S (2011) Preliminary results of a type-1 diabetes swine model. In 5th European IFMBE Conference, Budapest, Hungary, 307310.
- Farman M, Saleem MU, Meraj MA (2016) Control of Glucose Insulin Regulatory System for Type 1 Diabetes, Sci Int (Lahore) 28(1): 27-29.
- Chee G, Fernando T (2007) Closed-Loop Control of Blood Glucose. Number 368 in Lecture Notes in Control and Information Sciences. Springer Verlag, Berlin, Deutschland.
- Dalla Man C, Rizza RA, Cobelli C Meal simulation model of the glucoseinsulin system. IEEE Transactions on Biomedical Engineering, 54(10): 1740-1749.
- Khalil HK (2002) Nonlinear systems. Prentice hall (3rd edn).
- Stephen D Patek, Marc D Breton (2008) LQG Artificial Pancreas Control System and Related Method 6(5): 609-619.
- Hokayem PA, Gallestey E (2015) Lyapunov Stability Theory, non-linear systems and control.
- Bressan A, Piccoli B (2007) Introduction to the mathematical theory of control, volume 2 of AIMS Series on Applied Mathematics. American Institute of Mathematical Sciences (AIMS).
- Parker RS, Doyle FJI, Peppas NA (2001) The intravenous route to blood glucose control. a review of control algorithms for non-invasive monitoring and regulation in type i diabetic patients. IEEE Engineering in Medicine and Biology Magazine 20(1): 6573.
- Johnston SJ, Jafari H, Moshokoa SP, Ariyan VM, Baleanu D (2016) Laplace homotopy perturbation method for Burgers equation with space-and time-fractional order. Open Physics 14(1): 247-252.






























