L2-Boundedness of Integral Operators Involving3F2
Shahid Mubeen*
Department of Mathematics, University of Sargodha, Pakistan
Submission: May 5, 2017; Published: July 11, 2017
*Corresponding author: Shahid Mubeen, Department of Mathematics, University of Sargodha, Pakistan, Email : smjhanda@gmail.com
How to cite this article: Shahid M. L2-Boundedness of Integral Operators Involving 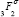 . Biostat Biometrics Open Acc J. 2017;2(2): 555583. DOI: 10.19080/BBOAJ.2017.02.555583
. Biostat Biometrics Open Acc J. 2017;2(2): 555583. DOI: 10.19080/BBOAJ.2017.02.555583
Abstract
In this paper, we formulate the integral operators 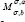 involving hypergeometric functions
involving hypergeometric functions 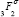 as kernel. We discuss that these operators are composition of Erdlyi-Kober fractional integral operators. We also discuss the boundedness of these integral operators in L2.
as kernel. We discuss that these operators are composition of Erdlyi-Kober fractional integral operators. We also discuss the boundedness of these integral operators in L2.
Keywords: Fractional integral transform; Liouville and Kober frac-tional integrals; Hypergeometric functions; Integral transform with hypergeometric functions in the kernel
There have made numerous investigations pertaining to integral operators involving various hypergeometric functions 2F1 and the confluent hypergeometric functions 1F1 as kernel [1-5]. Many authors also discussed the boundedness of integral opera- tors and used their mapping properties to derive inversion processes [6].
In this paper, we use the integral representation of hypergeomet- ric functions [7]
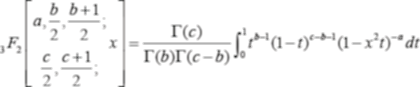
for formulating the integral operators of the following form
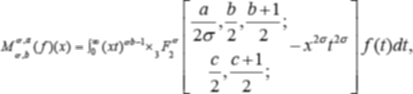
Where
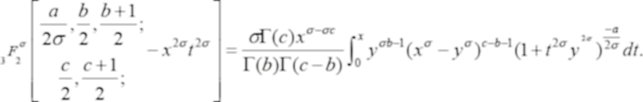
Here we start with a basic result that use later, see Karapetiants and Samko [8] and Okikiol
Lemma 1
Suppose that Ψ is a measurable and homogeneous function of degree -1 for all real numbers h i.e. 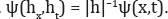 .
.
Let
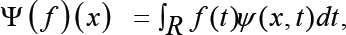
then
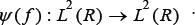
Also as a consequence, we have the L2-boundedness of generalized Erdlyi-Kober fractional integrals [10] as transcribed below.
Lemma 2
Let
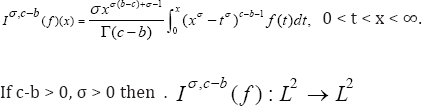
We now prove the boundedness of the following integral operators involving homogeneous functions as kernel. These integral operators are generalization of integral operators those are studied by Love [11] and Habibullah [12].
Lemma 3
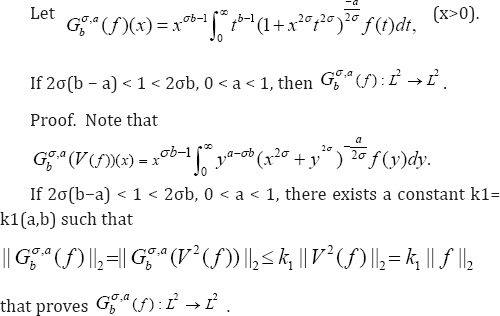
By using Fubini's theorem, we have the following lemma:
Lemma 4
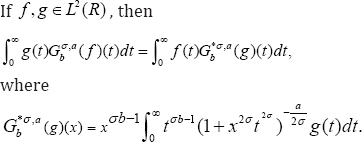
Lemma 5
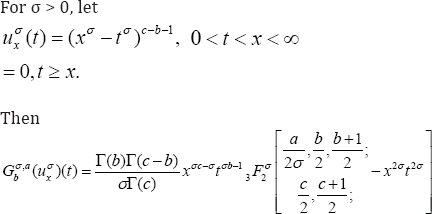
Proof. After making some substitutions in the integral representation of 3F2, we get the following integral
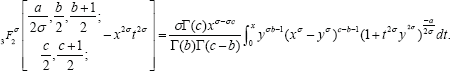
By replacing 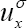 in place of g in Lemma 4, we have obtain
in place of g in Lemma 4, we have obtain
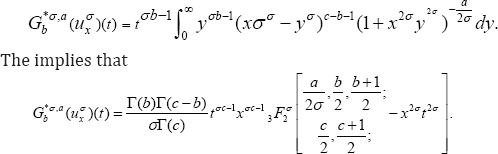
Now, we formulate integral operators 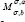 involving hypergeometric functions of the type
involving hypergeometric functions of the type 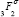 and then prove the boundedness of these integral operators in L2.
and then prove the boundedness of these integral operators in L2.
Thearem 1
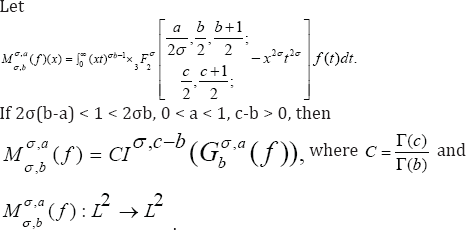
Proof. An application of Lemma 3 and Lemma 4 yields
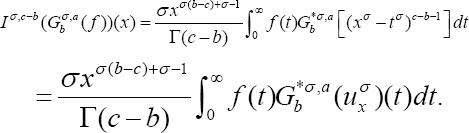
By using Lemma 5, we conclude that
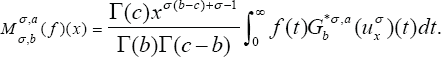
Consequently, it implies that
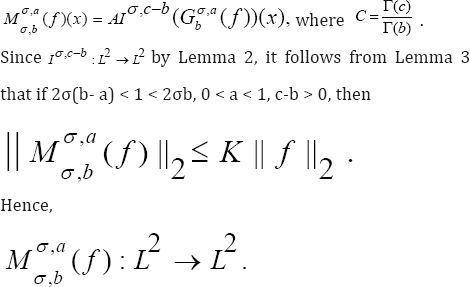
References
- Erdelyi A (1964) An integral equation involving Legendre functions. J Soc 12(1): 15-30.
- Higgins TP (1963) An inversion of integral for a Gegenbauer transformation. J Soc Indust Appl Math 11(4): 886-893.
- Anatoly AK, Saigo, Megumi, Trujillo JJ (2000) On the Meijer transform in space. Integral transforms and special functions 10(3-4): 267-282.
- Anatoly AK, Repin, Oleg A, Saigo, Megumi (2002) Generalized fractional integral transforms with Gauss function kernels as G-transforms. Integral transforms and special functions. 13(3): 285-307.
- Anatoly AK, Sebastian Nicy (2008) Generalized fractional integration of Bessel Function of the First Kind. Integral transforms and special functions 19(12): 869-883.
- Habibullah GM (1977) A note on a pair of integral operators involving Whit- taker functions. Glasgow Math J Soc 18: 99-100.
- Driver KA, Johnston SJ (2006) An integral representation of some hyper- geometric functions. Electronic Transactions on Numerical Analysis. 25: 115-120.
- Love ER (1967) Some integral equations involving hypergeometric functions. Proc Edinburgh Math Soc 15: 169-198.
- Erdelyi A (1950) On some functional representations. Univ E Politic Torino Rend Semi Math 10: 217- 234.
- Kober H (1940) On fractional integrals and derivatives. Quart J Math 11: 193-211.
- Karapetiants NK, Samko SG (1999) Multidimensional integral operators with homogeneous kernels. Fract Calc and Applied Anal, pp. 67-96.
- Okikiolu GO (1966) Bounded Linear Transformation in Space. Journal London Math Soc 41: 407-414.






























