Hybrid Parametric Optimality Constraints for Discrete Rivmax Fractional Programming
Ram U Verma*
Department of Mathematics, University of North Texas, USA
Submission: April 29, 2017; Published: June 02, 2017
*Corresponding author: Ram U Verma, Department of Mathematics, University of North Texas, USA, Email: verma99@msn.com
How to cite this article: Ram U V. Hybrid Parametric Optimality Constraints for Discrete Minmax Fractional Programming. Biostat Biometrics Open Acc 02 J. 2017;2(1): 555579. DOI: 10.19080/BBOAJ.2017.02.555579
Abstract
Several classes of generalized higher order parametric sufficient optimality constraints for a discrete minmax fractional programming problem are investigated toward establishing advanced results on higher order fractional programming. These results are established by applying advanced partitioning schemes and various types of generalized second-order (F,β,φ,π,ρ,θ,m)-univexity assumptions. The obtained results are new and generalize most of the results on (F,β,π,ρ,θ,m)-univexity in the literature.
Keywords: Discrete minmax fractional programming; Second-order univex functions; Generalized sufficient optimality conditions
Introduction
In this paper, we intend to establish several sets of generalized parametric sufficient optimality conditions for the following discrete minmax fractional programming problem:
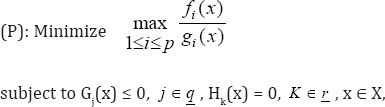

The present investigation is aimed at establishing various second-order necessary and sufficient optimality conditions for several types of optimization problems, using the generalized concepts of second-order invexity, pseudoinvexity, and quasiinvexity originally defined by Hanson [1], and a set of second-order necessary optimality conditions by introducing the new classes of generalized second-oder invex functions. We shall apply two partitioning schemes by Mond & Weir [2] and Yang [3] , in conjunction with the new classes of generalized second- order invex functions to formulate and discuss numerous sets of generalized second-order sufficient optimality conditions for (P). To the best of our knowledge, all the second-order sufficient optimality results established in this paper are new in the area of discrete minmax fractional programming and encompass most of the investigations in the literature. The generalized optimality conditions established here can be utilized for constructing some generalized second-order parametric duality models for (P) and proving numerous weak, strong, and strict converse duality theorems. For more details on the discrete minmax fractional programming and related literature, we refer the reader [1-9].
The rest of this paper is organized as follows. In the remainder of this section, we generalize a few basic definitions and recall some auxiliary results which will be needed in the sequel. In Section 2, we state and prove various second-order parametric sufficient optimality results for (P) using a variety of generalized (F,β,φ,π,ρ,θ,m)-sounivexity assumptions. Finally, in Section 3 we summarize our main results and also point out some further research opportunities arising from certain modifications of the principal problem investigated in the present paper.
We next define some new classes of generalized second- order univex functions, called (strictly) (F,β,φ,π,ρ,θ,m)-sounivex, (strictly) (F,β,φ,π,ρ,θ,m)-pseudosounivex, and (pre-strictly) (F,β,φ,π,ρ,θ,m)-quasisounivex functions. These are further extensions of the classes of second-order (strictly) (^/p,p,0,m)- sonvex, (strictly) (^,n,p,0,m)-pseudosonvex, and (prestrictly) (^,n,p,0,m)-quasisonvex functions which were introduced recently in [4]. The second-order univex functions are also referred to as “sounivex functions” in the litera-ture. For more on the generalized F-convex and other related functions, we refer the reader [8,9]. Now we present the new classes of (F,P/rc,9,p,0,m)-sounivex functions at x*. Let f : X ^ M be a twice differentiable function.
Definition
The function f is said to be (strictly) (F,β,φ,π,ρ,θ,m)- pseudosounivex at x* if there exist functions ρ: χxχ→R+ ≡(o,»), φ: ℝ→ℝ, ρ:X x X Rπ,, θ: X x X ℝn,Hybrid optimality constriants a sublinear function fx,x*’.): ℝ→ℝ , and a positive integer m such that for each xϵX(x≠x*) and , z ϵ ℝn
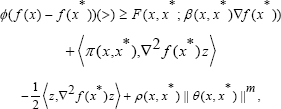
Where ‖. ‖ is a norm on ℝn and ≺a,b≻ is the innerproduct of the vectors a and b.The function f is said to be (strictly) (F,β,φ,π,ρ,θ,m)- pseudosounivex at X if it (strictly) (F,β,φ,π,ρ,θ,m)pseudosounivex at each x*ϵX.
Definition
The function f is said to be (prestrictly) (F,β,φ,π,ρ,θ,m)- pseudosounivex at x* if there exist functions ρ: χxχ→R+ ≡(o,»), φ: ℝ→ℝ, ρ:X x X Rπ,, θ: X x X ℝn, a sublinear function fx,x*’.): ℝ→ℝ and a positive integer m such that for each x£X
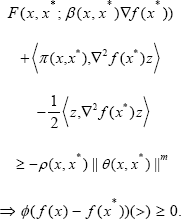
The function f is said to be (strictly) (F,β,φ,π,ρ,θ,m)- pseudosounivex on X if it is (strictly) (F,β,φ,π,ρ,θ,m)- pseudosounivex at each x*£X.
Definition
The function f is said to be (prestrictly) (F,β,φ,π,ρ,θ,m)- quasisounivex at x* if there exist functions ρ: χxχ→R+ ≡(o,»), φ: ℝ→ℝ, ρ:X x X Rπ,, θ: X x X ℝn, a sublinear function fx,x*’.): ℝ→ℝ and a positive integer m such that for each x£X
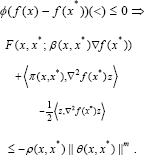
The function f is said to be (prestrictly) (F,β,φ,π,ρ,θ,m)- quasisounivex on X if it is (prestrictly) (F,β,φ,π,ρ,θ,m)- quasisounivex at each x*£X.
From the above definitions it is clear that if f is (F,β,φ,π,ρ,θ,m)- sounivex at x*, then it is both (F,β,φ,π,ρ,θ,m)-pseudosounivex and (F,β,φ,π,ρ,θ,m)-quasisounivex at x*, if f is (F,β,φ,π,ρ,θ,m)- quasisounivex at x*, then it is prestrictly (F,β,φ,π,ρ,θ,m)- quasisounivex at x*, and if f is strictly (F,β,φ,π,ρ,θ,m)- pseudosounivex at x*, then it is (F,β,φ,π,ρ,θ,m)-quasisounivex at x*.
In the proofs of the duality theorems, sometimes it may be more convenient to use certain alternative but equivalent forms of the above definitions. These are obtained by considering the contrapositive statements. For example, (F,β,φ,π,ρ,θ,m)- quasisounivexity can be defined in the following equivalent way: The function f is said to be (F,β,φ,π,ρ,θ,m)-quasisounivex at x* if there exist functions ρ: χxχ→R+ ≡(o,»), φ: ℝ→ℝ, ρ:X x X Rπ,, θ: X x X ℝn, a sublinear function fx,x*’.): ℝ→ℝ , and a positive integer m such that for each xϵX(x≠x*) and , z ϵ ℝn
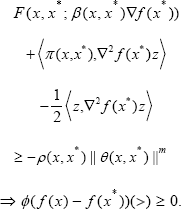
We conclude this section by recalling a set of second-order parametric necessary optimality conditions for (P). The form and features of this result will provide clear guidelines for formulating various sets of second-order parametric sufficient optimality conditions for (P).
Theorem
[4] Let x* be an optimal solution of (P), let λ* = ϕ(x*) be defined by
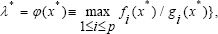

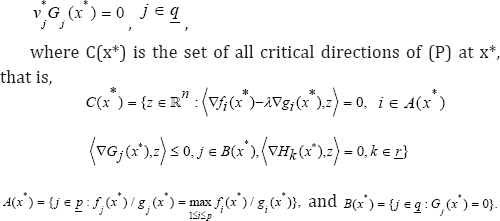
Second-Order Sufficient Optimality
In this section, we discuss several families of sufficient optimality results under various generalized (F,β,φ,π,ρ,θ,m)- sounivexity hypotheses imposed on certain combinations of the problem functions. This is accomplished by employing a certain partitioning scheme which was originally proposed in [2] for the purpose of constructing generalized dual problems for nonlinear programming problems. For this we need some additional notation.

In the proofs of our sufficiency theorems, we shall make frequent use of the following auxiliary result which provides an alternative expression for the objective function of (P).
Lemma
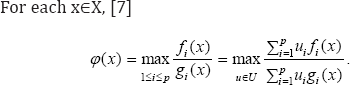
Making use of the sets and functions defined above, we can now formulate our first collection of generalized second-order parametric sufficient optimality results for (P) as follows.
Theorem
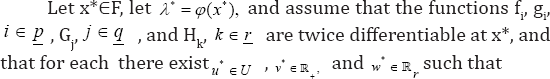
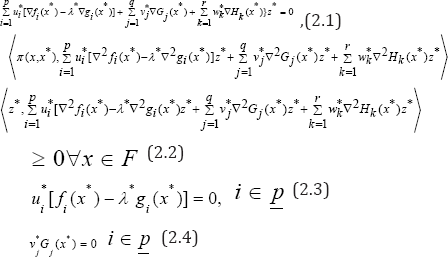
Assume, furthermore, that any one of the following four sets of hypotheses is satisfied:

Proof
Let x be an arbitrary feasible solution of (P).
(a) : In view of the sub linearity of f(x,x; ), it is clear that? (2.1) and (2.2) can be expressed as follows:

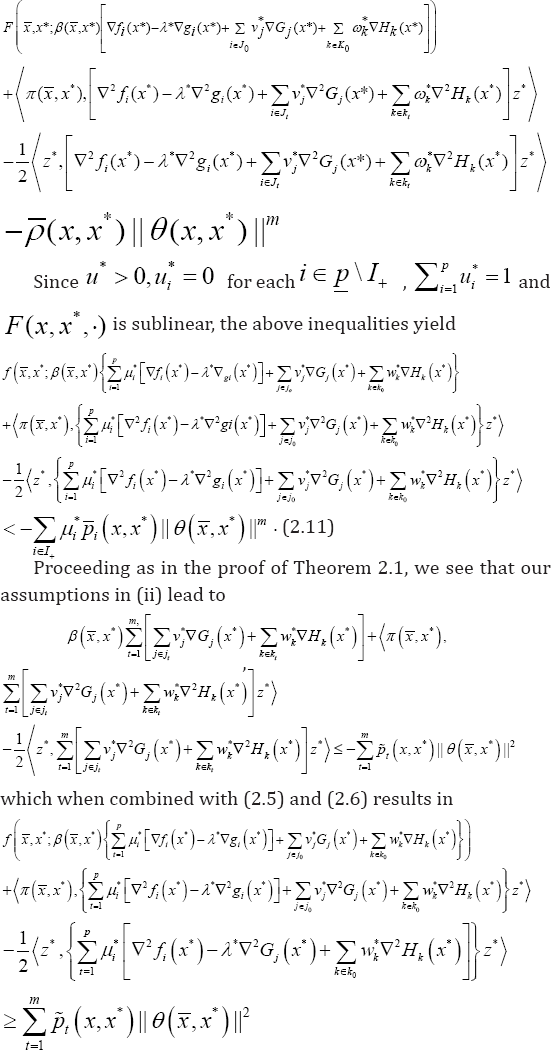
The rest of the proof is identical to that of part (a). (c) and (d): The proofs are similar to those of parts (a) and (b).
Theorem
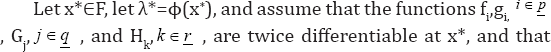

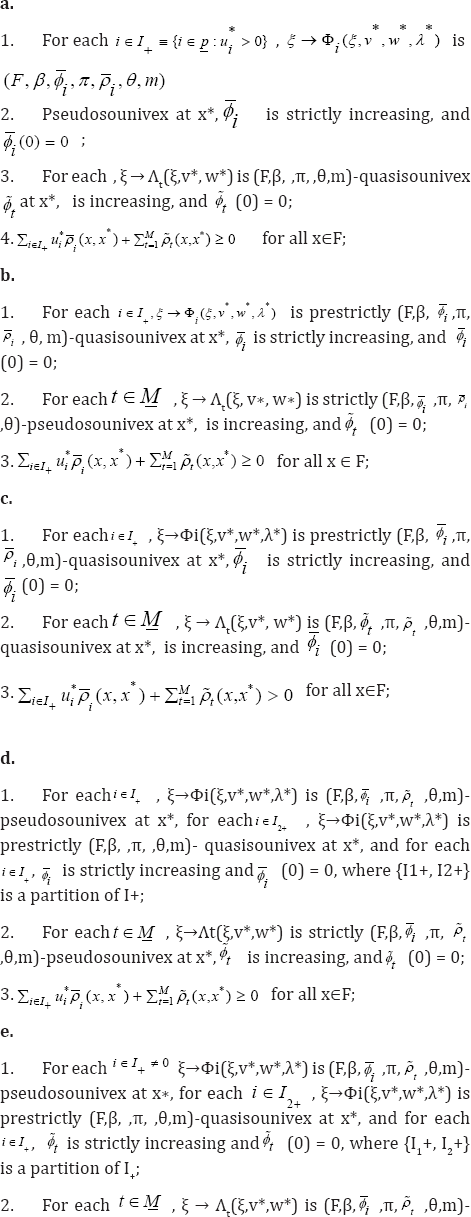
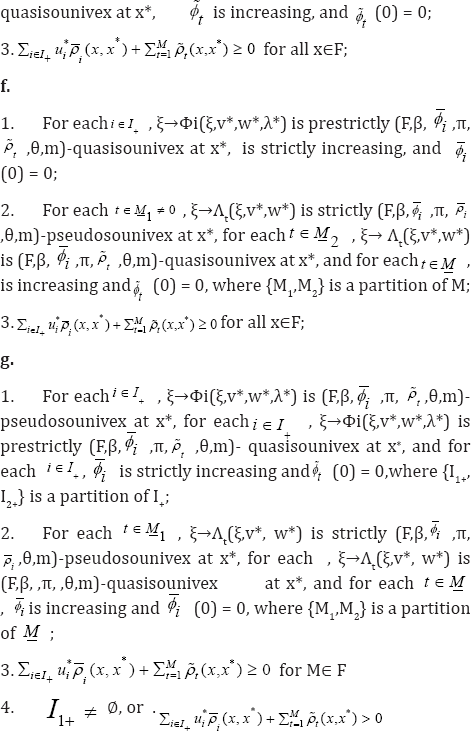
Then x* is an optimal solution of (P).
Proof


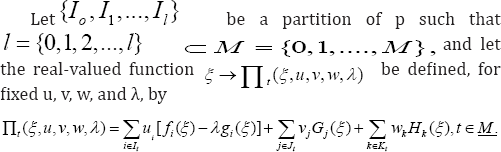
Theorem

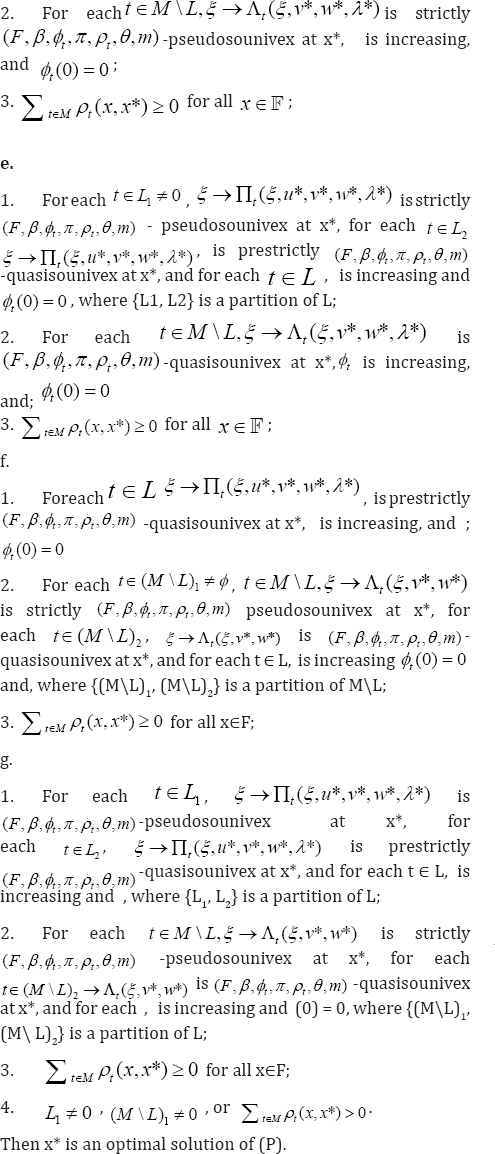
Proof(a)
(a) : Suppose to the contrary that x* is not an optimal solution of (P ). This implies that
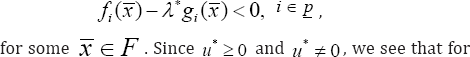

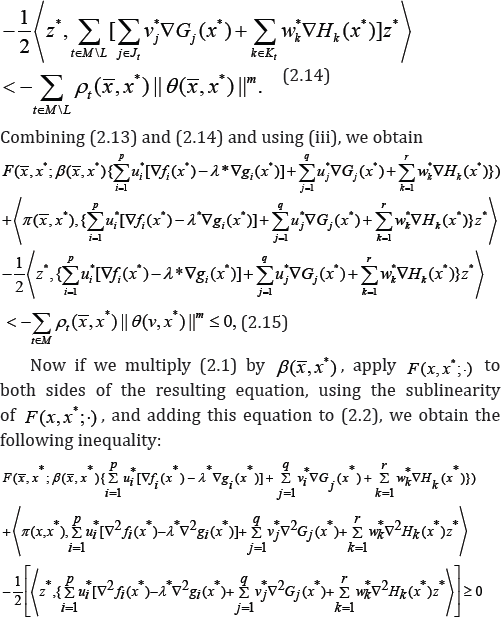
Concluding Remarks
Based on Dinkelbach’s parametric model [1], we have established numerous sets of higher order parametric sufficient optimality criteria for a discrete minmax fractional programming problem using a variety of generalized (F,β,φ,π,ρ,θ,m) -sounivexity constraints. These optimality models can be applied for constructing various duality models as well as for developing new algorithms for the numerical solution of minmax fractional programming problems. Furthermore, the obtained results generalize most of the results available in the semiinfinite aspects of the mathematical programming, for example, the following semiinfinite minmax fractional programming problem:
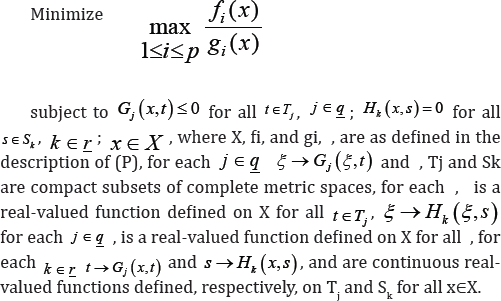
References
- Hanson MA (1993) Second order invexity and duality in mathematical programming. Opsearch 30: 313-320.
- Mond B, Weir T (1981) Generalized concavity and duality. In: Schaible S & Ziemba WT (Eds.), Generalized Concavity in Optimization and Economics, Academic Press, New York, USA, pp. 263-279.
- Yang X (1994) Generalized convex duality for multi objective fractional programs. Opsearch 31: 155-163.
- Dinkelbach W (1967) On nonlinear fractional programming. Management Sci 13: 492- 498.
- Verma RU, Zalmai GJ (2016) Second-order parametric optimality conditions in discrete minmax fractional programming. Communications on Applied Nonlinear Analysis 23(3): 1-32.
- Verma RU, Zalmai GJ (2016) Second order parametric optimality conditions in semi-infinite discrete minmax fractional programming based on second-order sonvexities. Transactions on Mathematical Programming and Applications 4(1): 62- 84.
- Zalmai GJ (1989) Optimality conditions and duality for constrained measurable subset selection problems with minmax objective functions, Optimization 20: 377-395.
- Zalmai GJ (2012) Generalized second-order (F,p,^,p,0)-univex functions and parametric duality models in semiinfinite discrete minmax fractional programming, Advances in Nonlinear Variational Inequalities 15: 63-91.
- Zalmai GJ, Zhang Q (2007) Generalized (F,p,^,p,0)-univex functions and global parametric sufficient optimality conditions in semiinfinite discrete minmax fractional programming, Pan American Mathematical Journal 17: 1-26.






























