Abstract

This letter reconsiders firm-level productivity decomposition in light of structural changes induced by artificial intelligence (AI). Standard frameworks, such as the Griliches-Regev and Foster-Haltiwanger-Krizan decompositions, are ill-suited to capture the heterogeneity, intangible complementarities, and reallocation dynamics introduced by AI adoption. We propose an extension to the standard production function that explicitly incorporates AI-specific capital, absorptive capacity, and intangible assets. This allows for a reinterpretation of within-firm and between-firm productivity effects under conditions of technological diffusion. The paper provides a conceptual basis for adapting decomposition techniques and highlights the measurement implications for applied researchers and statistical agencies.

Keywords:Total Factor Productivity; Decomposition Techniques; Artificial Intelligence JEL Code: D22, D24, L11, O47

Introduction

The diffusion of artificial intelligence (AI) across sectors requires a reassessment of how productivity is measured and decomposed. This letter illustrates how economists, social scientists and management studies might address this issue in respect of productivity decomposition techniques. Traditional frameworks do not account for the heterogeneous, intangible, and non-linear effects associated with AI adoption. AI alters production through labour substitution and complementarity with organizational capital. Its impact therefore varies across firms. Established decomposition techniques were not designed for these dynamics and risk not capturing all the productivity gains AI delivers.

AI technologies substitute for both routine and cognitive labor. This can be in non-linear and task specific ways. We suggest that this violates the assumption of smooth substitution as presented in classical production functions. AI also induces heterogeneous firm responses. We suggest these increase the dispersion of productivity. Meanwhile, productivity focused firms are more likely to integrate AI effectively. In theory, this would expand their market share at the expense of laggards. This dynamic intensifies reallocation of resources, thereby representing another key driver of productivity growth that is not captured in decomposition models.

Decomposition techniques break down the effects of firm level dynamics. As such, we think they are a valuable way to access AI’s roll put. They do so by decomposing productivity into within firm and entry and exit effects within markets. Our letter therefore contributes to ongoing methodological re-evaluation by comparing four leading decomposition approaches. We assess their capacity to capture within-firm improvements, reallocation effects, and entry-exit dynamics. Each method offers corrections to limitations in earlier models, such as reference bias and omitted covariance terms.

In the context of AI diffusion, measurement matters. Productivity gains may arise not only from innovation, but from structural shifts in market composition. Methodology should provide a more accurate lens through which to observe these changes, and should guide empirical work in this area.

Productivity Decomposition Techniques

We contend that existing empirical and theoretical frameworks require recalibration to account for how AI is reshaping production processes. As AI technologies diffuse through the economy, the assumption of homogeneous productivity responses embedded in representative decomposition models becomes increasingly untenable. We argue that this heterogeneity, coupled with the growing role of intangible complementarities and dynamic reallocation, necessitates a reconsideration of techniques.

We base our suggestion on the observation that AI alters the production process by both substituting for and complementing human capital across a range of tasks. It changes the marginal productivity of inputs and the efficiency of input-output transformation, thereby modifying the structure of the production function itself.

At the firm level, AI automates routine and cognitive tasks such as document classification and customer service. This shifts the role of labor and challenges the fixed substitution assumptions of the Cobb-Douglas framework Douglas [1]. For instance, the use of large language models (LLMs) in financial analysis increases analytical throughput. A logical approach would be to consider an extension to incorporate AI as a distinct input into the production function. We show how this can be done in equation 6, having explained the various effects in more detail.

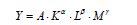
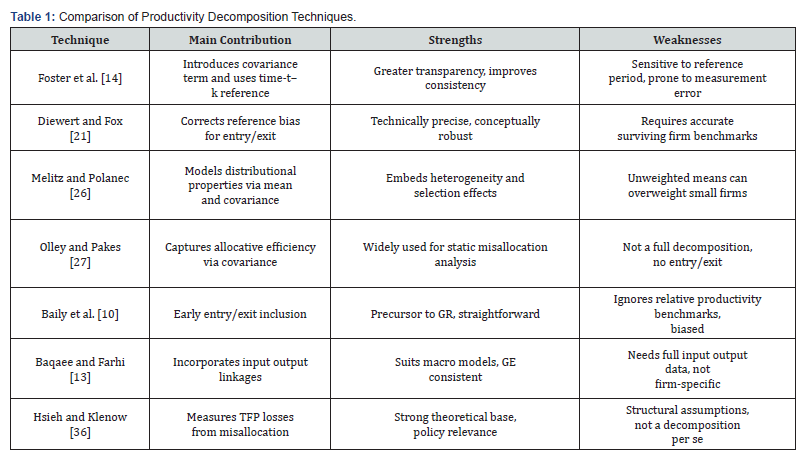
Table 1 serves to synthesize the principal decomposition techniques employed in the analysis of productivity dynamics. Its inclusion provides a methodological benchmark that clarifies the conceptual and empirical tradeoffs across approaches. In particular, it situates the four methods evaluated within a wider body of literature concerned with measuring firmlevel contributions to aggregate productivity. The relevance to our analysis lies in the ability of these techniques to address heterogeneous firm responses, selection dynamics, and the role of reallocation under conditions shaped by technological diffusion. As argued throughout, the emergence of AI intensifies the need for decomposition methods to be updated, so that they can isolate within-firm AI productivity gains from re-allocation and entry-exit effects.

Traditional productivity metrics, often grounded in representative agent frameworks, have long been critiqued for their inability to account for heterogeneity across firms and sectors. In this respect, we are merely extending the critique to encompass AI productivity gains. An early but theoretical debate on the deficiency of representative agent models to properly capture aggregate productivity dynamics already started in the early 1970s, with the works of Griliches and Ringstad [2], Nelson and Winter [3], and Griliches [4].

According to these authors, it was the variability within the population of firms that drove changes in TFP.

The following techniques are past and present attempts to empirically cement this argument, giving validity to early structural models of financial allocation and the micro-level behavior of firms1. The rise of AI intensifies the need to distinguish between different sources of productivity. AI technologies are not adopted uniformly. Their effects depend on firm size, absorptive capacity, sectoral structure, and complementary intangibles. As such, we suggest that the aggregate impact of AI cannot be adequately captured by representative agent models. A disaggregated approach is therefore required to understand whether AI productivity gains originate from within-firm improvements, reallocation of market share towards more innovative firms that adopt AI, or the process of firm entry and exit.

In response, productivity decomposition techniques have been developed that partition aggregate TFP growth into distinct components. First, the within effect which captures productivity growth within surviving firms. Second, the between or reallocation effect that empirically measures how market shares are reallocated between surviving firms with different productivity levels. And lastly, net entry which captures the effect of entering and exiting firms within an industry. In the context of AI, there will likely be a clear differentiation between the winners and losers due to the reallocation effect. Fundamentally, the models start from the assumption that industry-level productivity is the weighted average of firm-level productivity, see equation (1):

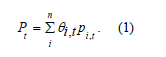
Where P_t is log of industry-level productivity, θ_i,t is the firmindustry share for firm i and sums up to 1,p_i,t,is log of firm-level productivity, and n is the total number of firms within the industry2. All decomposition techniques can be seen as empirical refinements or conceptual expansions of this equation, Griliches and Regev [9] To analyze productivity dynamics within the Israeli mining and manufacturing sector between 1979 and 1988, Griliches and Regev created the following decomposition method:

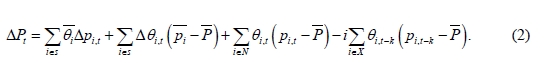
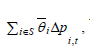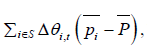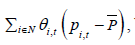Equation (2) decomposes the growth rate of industry productivity into four different factors; first, which is the within effect. Second, which is the reallocation/between effect. Third, which is the entry effect. And, lastly, the exit effect 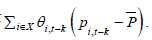The letter S signifies surviving firms, or the firms that are present in t −1 and t, N are the entering firms, or the firms that enter in t, and X are the exiting firms, or the firms that exit in t −1 and are therefore not present in t.A bar over the variable signifies the time average over the base year and the end year, that is, P is the reference productivity level computed as .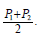

The development of such a decomposition technique was unprecedented by that time and therefore allowed researchers to see which margin would drive an expansion or contraction of industry productivity. One big development was that the between and net entry effects are deviations from their respective industry averages at time t and t − k instead of absolute ending-level plant-level productivity endowments3.

Barwick et al. [11] use the Griliches and Regev method to analyze entry deregulation, market turnover, and efficiency during China’s business registration reform, starting locally but later being covered by the entire country. Their analysis shows that the reform increased firm entry by 25% and firm exit by 8.7% in the manufacturing sector. Studying the relationship between environmental regulations and export upgrading from the perspective of the domestic value-added rate of exports, Sun et al. [12] observe an increase in domestic productivity in cleaner export production for the years between 2000 and 2011. Lastly, to measure the effects of distortions such as taxes, markups, frictions to resource reallocation, financial frictions, and nominal rigidities on an economy, Baqaee and Farhi [13] us the Griliches and Regev method to find that microeconomic shocks could reduce nationwide TFP by almost 15%.

Foster, Haltiwanger, and Krizan [14] To analyze micro-level patterns and their relationship to aggregate TFP in the US from 1972 to 1992, Foster et al. developed another decomposition technique a few years later.

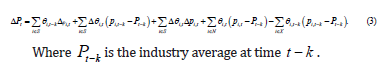
The Foster et al. decomposition, equation (3), shares the same components as the one developed by Griliches and Regev. That is, a within, between, and net entry effect. However, it has an additional covariance term,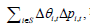 measuring the cross effects of changes in market shares and changes in productivity levels. The authors argue that decomposing industry-level productivity in this way is important to make the interpretation more transparent and consistent. They show that the Griliches and Regev decomposition contains the covariance effect partly in its within and partly in its between effect, rendering results problematic at best, and inconsistent at worst4,5. A technical difference of this method is that instead of averaging out output shares and productivity levels over the beginning and end periods, industry average productivity levels at time t − k to compare current productivity dynamics are used.

Analyzing the impact of Covid-19 on productivity, Bloom et al. [18] use the Foster et al. decomposition technique in conjunction with data from an innovative monthly firm survey that asks for quantitative impacts of Covid-19 on inputs and outputs. They find that US TFP fell by up to 6% during 2020–2021. Liu [19] studies the adoption of the Uniform Trade Secrets Act (UTSA). Finding a 5.1% increase in employment among affected public firms, he argues that effects are concentrated in firms with below-median initial employment, higher debt costs, and greater potential for knowledge spillovers. R&D expenditures and the accumulation of intangible assets emerge as key drivers of these employment effects. Lastly, analyzing employer market power in US manufacturing and how it has changed from the 1970s to early 2000s, Yeh et al. [20] use the Foster et al. decomposition and find that most manufacturing plants that operate in a monopsonistic environment experience an average markdown of 1.53, implying a worker earning only 65 cents on the marginal dollar generated.

Diewert and Fox [21] A critical development in decomposing industry-level productivity into its components was the technique introduced by Diewert and Fox [21]. Their methodology was built to eliminate the bias caused by incorrect reference levels used by both, FHK and GR, when calculating the effect of entry and exit on industry-level productivity growth. This bias arises because the reference level with which entering and exiting firms are compared is not the actual productivity level of surviving firms at the time of exit or entry. Table 2 shows their differences.

As Table 2 illustrates, for GR and FHK, the benchmark against which entering and exiting firms are compared is respectively the same. This means that firms that enter and firms that exit are compared with firms that have not changed in their productivity levels from time t − k to time t (FHK), or have changed between both time periods but are averaged out (GR)6. This, however, is inaccurate. Between both periods, productivity growth evolves and therefore entering firms need to be compared to surviving firms at the time of entry and exiting firms must be compared to surviving firms at the time of exit. Disregarding this will introduce a bias that overestimates the net entry effect if industry-wide TFP is increasing, and underestimates net entry if industry-wide TFP is decreasing. To account for this major shortcoming, Diewert and Fox develop the following decomposition technique, equation (4):

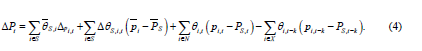
Compared to before, the first term is the within and the second the reallocation effect. The third and fourth terms are the mechanically updated entry and exit effects, respectively. With the help of the last two terms, Diewert and Fox solve the issue of incorrect reference levels by comparing entry in time t and exit at time t − k with the productivity level of surviving firms in the same time period. The rational behind this is that only entering (exiting) firms that have a higher (lower) than surviving firms productivity will increase industry-level productivity growth. This eliminates the bias of the aforementioned decomposition techniques and is therefore technically as well as conceptually preferable7.

To measure productivity outcomes of Finland’s ICT industry, Kuosmanen and Kuosmanen [22] use the Diewert and Fox decomposition to investigate whether productivity growth is driven within or between industries. We note that finlands ICT industry is an early adopted or AI. For the recent two decades, the authors find that the sharp decline of labor productivity was associated with structural changes, whereas the surviving firms that continued in the same industry managed to improve their productivity. Focusing on the Global Financial Crisis in the UK, Gerth et al. [23] discover that the main factor driving the aggregate TFP decline is the within effects. However, the entry and exit effects also significantly contribute to the long-lasting drop in aggregate TFP. First, exiting firms tend to have higher than average TFP. Second, newly entering firms tend to have lower than average TFP. And third, newly entering firms fail to increase their TFP levels over time, thereby depressing the within effect. Also using the Diewert and Fox decomposition, Cunningham et al. [24] study the nature of competition and frictions within different sectors in the economy, focusing on the sources of rising wage inequality across businesses. They conclude that productivity dispersion across businesses can provide information about these potential shortfalls in efficient allocation. Lastly, for the US between 1996 and 2012, Alon et al. [25] find that declining firm entry and the aging incumbent firms have meaningful implications for sluggish labour aggregate productivity growth. They discover that the relationship between firm age and productivity growth is downward sloping and convex, the magnitudes are substantial but fade quickly, and selection and reallocation predominantly drive higher productivity growth of young firms.

Melitz and Polanec [26] Melitz and Polanec support Diewert and Fox’s argument about the importance of using the appropriate reference level. For the Slovenian economy, the authors find that the GR and FHK decompositions substantially overestimate net entry and consequently underestimate the contribution of surviving firms. Between 1995 and 2000, Melitz and Polanec estimate the magnitude of the measurement bias to be between 7 and 10 percentage points of an aggregate productivity growth of 50%. We would suggest such measurement biases will only get biggeras AI rolls out and reallocation effects become more prevalent.

In addition to measuring net entry in a consistent manner, the MP decomposition models the first two moments of a joint probability distribution between firm-level productivity and market share, see equation (5):

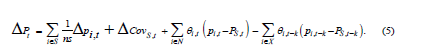
Where, unlike the other decomposition techniques, the first term represents the unweighted firm productivity mean and captures the shifts of the productivity distribution in terms of its measure of location8. The second term is the reallocation or covariance term between firm productivity and output shares and represents the second moment of P the joint productivity-market share distribution. In its full expression, Cov_S,t is equal to

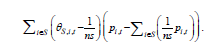
The two first terms not only represent the static Olley and Pakes [27] productivity decomposition, but also carry a very convenient feature; since they are based on two specific moments of a productivity density distribution, they can be more easily embedded into structural models of firm heterogeneity and resource misallocation and their effects on aggregate productivity dynamics9.

To estimate green TFP as a proxy for the green transformation in China, Yu et al. [32] use a model that is based on the decomposition by Melitz and Polanec. These authors find that reforming counties into municipal districts, resource allocation is optimized. Especially, positive effects are more pronounced for district- and county-level enterprises, capital-intensive firms, and industries with high external financing dependency. Decker et al. [33] study the pace of job reallocation in the US for the last few decades. Observing a decline in the reallocation of resources between firms, the authors find that the responsiveness of business-level employment to productivity has weakened during the observation period. We observe that the AI roll out differs at a country level, and this could be the basis for future research.

The US is arguably leading in the roll out of AI. Using micro panel data from the US Economic Census since 1982, Autor et al. [34] assess the fall in the US labour share due to the entry and rise of high-productivity firms. They argue that if technological changes push sales toward the most productive firms in each industry, product market concentration will rise as industries become increasingly dominated by superstar firms, which have high markups and a low labor share of value added.

Conceptual Framework for AI-Augmented Productivity

The emergence of AI, and LLMs in particular, raises fundamental questions about how productivity gains are realized across an economy. Traditional productivity decomposition techniques, such as those described allow researchers to attribute aggregate TFP growth to firm-level dynamics including withinfirm improvements [35-37].

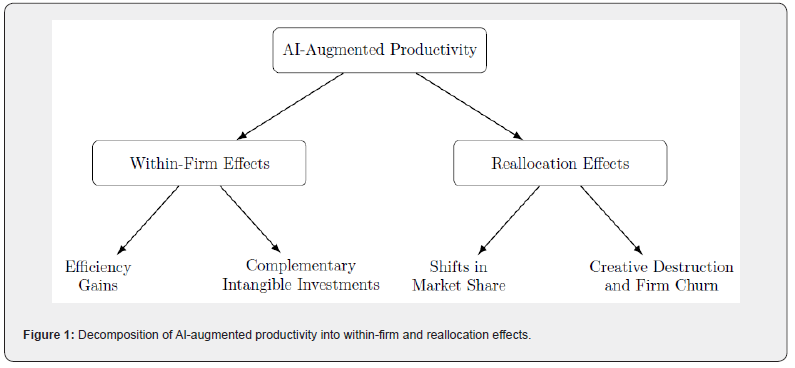
In this section, we propose a conceptual framework that links AI-related technological change to the channels of productivity growth identified in the literature. This framework synthesis empirical insights from decomposition techniques with theoretical arguments on firm heterogeneity and resource misallocation. Specifically, it distinguishes between within-firm effects, such as improvements in technical efficiency and the deployment of complementary intangibles (e.g. proprietary datasets or organizational know-how), and between-firm reallocation mechanisms, including market share shifts and the churn of less productive firms.

Figure 1 illustrates the conceptual framework explaining the structure of AI-augmented productivity. The diagram presents two principal channels through which AI adoption affects aggregate productivity: (1) within firm effects, where gains stem from internal improvements in processes and capabilities, and (2) reallocation effects, where the macro impact is driven by competitive dynamics and structural transformation in response to AI. These pathways map directly onto the analytical constructs used in productivity decomposition models and provide a theoretical basis for the empirical analysis that follows..

Structural Interpretation of Decomposition Under AI

While Figure 1 outlines the conceptual channels through which AI influences productivity, we propose anextension to the standard production framework that explicitly captures these dynamics. In particular, we allow for heterogeneity in AI adoption, firm-specific absorptive capacity, and the role of complementary intangibles.

We modify the conventional Cobb-Douglas function to incorporate AI-specific inputs as follows:

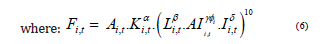
•F_i,t denotes output of firm i at time t ,
• A_i,t is firm-level TFP,
• K_i,t and L_i,t are physical capital and labor inputs, respectively,
•AI_i,t is the stock of AI-specific capital,
• φ_i ∈[0,1] denotes the firm’s absorptive capacity for AI (e.g., data infrastructure, integration),
•I_i,t captures intangible capital such as proprietary datasets or organizational routines,
• α + β + γ +δ = 1 under constant returns to scale.

This formulation allows the marginal effect of AI capital to be modulated by a firm’s organizational readiness (φ_i)and the presence of complementary intangible inputs (I_i,t) . Both vary across firms and sectors, introducing non-uniform productivity responses.

This has direct implications for how we interpret productivity decomposition:

Within-firm effects. These now capture not only technical efficiency gains (ΔF_i,t) , but also internal improvements from increased AI use (AI_i,t) enhanced absorptive capacity (φ_i)and investment in intangibles (I_i,t) . For firms undergoing successful digital transformation, this term becomes the principal driver of productivity gains.

Reallocation effects. As AI leads to scale economies and diverging firm capabilities, market shares shift towards high φ_i − and, high (I_i,t firms. The covariance between productivity and firm size increases, intensifying the between-firm reallocation term.

Net entry effects. Entry and exit dynamics evolve under AI diffusion. Entrants may have AI-native capabilities but underdeveloped intangibles; exiting firms may fail not due to low productivity per se, but due to an inability to integrate AI with legacy systems. These subtleties can be misrepresented unless decomposition benchmarks entry and exit against contemporaneous survivors.

By extending the production function and reinterpreting decomposition margins accordingly, we provide a structural foundation for aligning empirical measurement with the realities of the AI economy. These adjustments are not just theoretical refinements; they are prerequisites for any meaningful evaluation of how AI affects aggregate productivity.

Illustrative Implications or Measurement Implications

While this letter does not present new empirical estimates, it highlights the importance of selecting appropriate decomposition techniques when analyzing productivity dynamics in the context of AI diffusion. The implications of this choice are not merely technical. They shape how we interpret the mechanisms through which aggregate productivity evolves and, by extension, how policy and investment decisions are informed. The methodological revisions proposed in this letter carry direct implications for statistical agencies and productivity commissions.

To illustrate, consider an economy undergoing rapid adoption of AI technologies. If one were to use a Griliches-Regev framework, the net entry effect would be benchmarked against an average of productivity levels across two periods. In a setting where AI leads to accelerated divergence between frontier and laggard firms, such an averaging approach would obscure the true contribution of firm turnover. Similarly, if the Foster-Haltiwanger-Krizan method is used without adjustment for the covariance effect, the role of allocative efficiency may be overstated in periods when output is measured imprecisely or when intangible capital is unobserved.

More recent techniques, such as Diewert-Fox or Melitz- Polanec, correct for these limitations. They offer empirically implementable refinements that are conceptually aligned with the characteristics of AI-led transformation: firm heterogeneity, entryexit churn, and the growing salience of intangible inputs. While implementation requires granular firm-level data, the conceptual underpinnings of these techniques are broadly applicable. Their adoption would lead to more credible productivity analysis and, crucially, prevent misguided conclusions about the sources and sustainability of observed productivity trends. The objective here is not to adjudicate between techniques in a data-driven manner, but to underscore the methodological urgency for rethinking how we measure productivity in the face of technological discontinuity.

Conclusion

This letter calls for a revision of productivity measure techniques in light of the structural transformations associated with AI. Our purpose has not been empirical estimation, but rather to urge the economics profession to reconsider its approach in an era of accelerating technological change. The methodological tools already exist. However, their adoption remains uneven, and too often empirical work relies on legacy frameworks that obscure the very dynamics we seek to understand.

AI challenges conventional assumptions embedded in representative firm models and additive production functions. It introduces heterogeneity in adoption, complements intangible assets, and reshapes reallocation dynamics across sectors. Decomposition techniques that ignore these features risk misattributing the sources of productivity change, particularly during periods of disruption. Newer methods, such as those of Diewert-Fox and Melitz-Polanec, are better equipped to capture the structural and allocative forces at play, especially under conditions of firm turnover and intangible capital deepening.

We argue that economists must align measurement practices with the realities of the digital economy. This requires abandoning overly simplistic models in favour of approaches that reflect how AI diffuses, interacts with organizational structures, and alters the margins of adjustment. Doing so will not only improve the accuracy of productivity analysis, but also enable more informed policy responses. The time to recalibrate our empirical frameworks is now.

Acknowledgment

The authors would like to thank the participants of the International Conference on Empirical Economics at PSU Altoona for helpful comments and suggestions.

References

1. Douglas PH (1948) Are there laws of production? American Economic Review 38 (1): 1-41.
2. Griliches Z and Ringstad V (1971) Economics of scale and the form of the production function: an econometric study of Norwegian manufacturing establishment data. Amsterdam: Holland, North Pub Co.
3. Nelson RR and Winter SG (1978) Forces Generating and Limiting Concentration under Schumpeterian Competition. The Bell Journal of Economics 9(2): 524-548.
4. Griliches Z (1979) Issues in assessing the contribution of research and development to productivity growth. The Bell Journal of Economics 10(1): 92-116.
5. Jovanovic B (1982) Selection and the Evolution of Industry. Econometrica 50(3): 649-670.
6. Griliches Z and Mairesse J (1983) Comparing Productivity Growth: An Exploration of French and U.S Industrial and Firm Data. European Economic Review 21(1-2): 89-119.
7. Olley SG and Pakes A (1996b) The Dynamics of Productivity in the Telecommunications Equipment Industry. Econometrica 64(6): 1263-1297.
8. Bartelsman EJ and Dhrymes PJ (1998) Productivity Dynamics: U.S. Manufacturing Plants, 1972-1986. Journal of Productivity Analysis 9: 5-34.
9. Griliches Z and Regev H (1995) Firm productivity in Israeli industry 1979-1988. Journal of Econometrics 65: 175-203.
10. Baily MN, Hulten C, and Campbell D (1992) Productivity dynamics in manufacturing plants. Brookings Papers on Economic Activity: Microeconomics, pp. 187-267.
11. Barwick PJ, Chen L, Li S, and Zhang X (2025) Entry deregulation, market turnover, and efficiency: China’s business registration reform. Review of Economics and Statistics, p. 1-46.
12. Sun C, Zhan Y, and Gao X (2023) Does environmental regulation increase domestic value-added in exports? an empirical study of cleaner production standards in china. World Development 163: 106154.
13. Baqaee DR and Farhi E (2020) Productivity and misallocation in general equilibrium. The Quarterly Journal of Economics 135 (1): 105-163.
14. Foster L, Haltiwanger JC, and Krizan CJ (2001) Aggregate Productivity Growth Lessons from Microeconomic Evidence. In: Hulten C, Dean ER, and Harper MJ (Eds.), New Developments in Productivity Analysis, University of Chicago Press, Chapter 8, pp. 303-375.
15. Disney R, Haskel J, and Heden Y (2003) Restructuring and productivity growth in uk manufacturing. The Economic Journal 113(489): 666-694.
16. Fukao K and Kwon HU (2006) Why did Japan’s TFP Growth Slow Down in the Lost Devade? An Emprirical Analysis based on Firm-Level Data of Manuracturing Firms. The Japanese Economic Review 57(2): 195-228.
17. Riley R, Rosazza-Bondibene C, and Young G (2015) The UK productivity puzzle 2008-13: evidence from British businesses. Bank of England Staff Working Papers.
18. Bloom N, Bunn P, Mizen P, Smietanka P, and Thwaites G (2025) The impact of covid-19 on productivity. Review of Economics and Statistics 107(1): 28-41.
19. Liu AY (2025) Trade secrets protection and employment of public firms: Evidence from the uniform trade secrets act. Research Policy 54(6): 105243.
20. Yeh C, Macaluso C, and Hershbein B (2022) Monopsony in the us labor market. American Economic Review 112(7): 2099-2138.
21. Diewert WE and Fox KJ (2010) Price and Productivity Measurement: Index Number Theory. In: Diewert WE, Balk BM, Fixler D, Fox KJ, and Nakamura AO (Eds.), Chapter On Measuring the Contribution of Entering and Exiting Firms to Aggregate Productivity Growth, Trafford Press, pp. 41-66.
22. Kuosmanen N and Kuosmanen T (2024) Inter-industry and intra-industry switching as sources of productivity growth: Structural change of finland’s ict industries. Journal of Productivity Analysis 61(2): 107-120.
23. Gerth F, Briggs CM, and Diaz JFT (2024) Exit and entry dynamics of uk firms in the wake of the global financial crisis. Munich Personal RePEc Archive - Working Paper Series (123325): 1-19.
24. Cunningham C, Foster L, Grim C, Haltiwanger J, Pabilonia SW, et al. (2023) Dispersion in dispersion: Measuring establishment-level differences in productivity. Review of Income and Wealth 69(4): 999-1032.
25. Alon T, Berger D, Dent R, and Pugsley B (2018) Older and slower: The startup deficit’s lasting effects on aggregate productivity growth. Journal of Monetary Economics 93: 68-85.
26. Melitz MJ and Polanec S (2015a) Dynamic olley-pakes productivity decomposition with entry and exit. The RAND Journal of Economics 46(2): 362-375.
27. Olley SG and Pakes A (1996a) The dynamics of productivity in the telecommunications equipment industry. Econometrica 64 (6): 1263-1297.
28. Hsieh CT and Klenow PJ (2009b) Misallocation and Manufacturing TFP in China and India. The Quarterly Journal of Economics CXXIV (4): 1-55.
29. Collard-Wexler A and De Loecker J (2015) Reallocation and Technology: Evidence from the US Steel Industry. American Economic Review 105(1): 131-171.
30. Bartelsman EJ, Haltiwanger JC, and Scarpetta S (2013) Cross-Country Differences in Productivity: The Role of Allocation and Selection. The American Economic Review 103(1): 305-334.
31. Gerth F, O’Brien M, and Briggs CM (2025) Allocative efficiency of uk firms during the great recession. Applied Economics Letters, 1-6.
32. Yu X, Zhou J, Ni K, and Wang X (2025) Environmental centralization and firm green transition: Evidence from county-to-district reclassification in china. Energy Economics 144: 108365.
33. Decker RA, Haltiwanger J, Jarmin RS, and Miranda J (2020) Changing business dynamism and productivity: Shocks versus responsiveness. American Economic Review 110(12): 3952-3990.
34. Autor D, Dorn D, Katz LF, Patterson C, and Van Reenen J (2020) The fall of the labor share and the rise of superstar firms. The Quarterly journal of economics 135(2): 645-709.
35. Baily MN, Hulten C, Campbell D, Bresnahan T, and Caves RE (1992) Productivity Dynamics in Manufacturing Plants. Brookings Papers on Economic Activity, pp. 187-267.
36. Hsieh CT and Klenow PJ (2009a) Misallocation and manufacturing tfp in china and india. Quarterly Journal of Economics 124 (4): 1403-1448.
37. Melitz MJ and Polanec S (2015b) Dynamic Olley-Pakes productivity decomposition with entry and exit. The RAND Journal of Economics 46(2): 362-375.