F Dubeau

doi:10.19080/ASM.2019.03.555611

Review Article

Behavior Related to Taxation System: Example of Bi-Criteria Linear Program for Animal Diet Formulation

F Dubeau*

Department of Mathematics, University of Sherbrooke, Canada

Submission: July 23, 2018;Published: April 30, 2019

*Corresponding author: F Dubeau, Department of Mathematics, University of Sherbrooke 2500, Boulevard of University, Sherbrooke, Canada

How to cite this article:F Dubeau. Behavior Related to Taxation System: Example of Bi-Criteria Linear Program for Animal Diet Formulation. Ann Soc Sci Manage Stud. 2019; 3(3): 555611. DOI: 10.19080/ASM.2019.03.555611

Abstract

The Pareto set of a mathematical model is a useful tool for a decision maker in case of conflicting criteria. This Pareto set contains all the information on the behavior resulting from an optimal decision. For a linear model, this Pareto set shows abrupt (discrete) changes in the behavior depending on the weight, or the tax, associated to the criteria. Moreover, for a bi-criteria linear model, the Pareto curve in the criteria space is a simple polygonal curve. We illustrate those facts by solving the pig diet formulation problem which considers not only the cost of the diet but also its environmental impact based here on the phosphorus excretion related to the diet.

Keywords: Behavior; Taxation System; Bi-Criteria Linear Program; Pareto Set; Weighted-Sum; Diet Formulation

Introduction

Animal diet formulation is a very important problem from an economic and environmental point of view, so it is an interesting example in the field of operations research. Many modern animal diet formulation methods tend to consider not only the cost of the diet but also excretions that are detrimental from an environmental point of view. Following [5], it is appropriate to apply a tax on excretions to change the behavior of the producers in the swine industry. These changes in behavior are studied using a formulation of the problem as a bi-criteria model and are obtained by the determination of its Pareto set. For linear models, the changes in behavior of the producer are abrupt (discrete) and correspond to specific values of the tax. In other words, even in increasing the tax it can happen that there is no change in the behavior of the producer. Behavior changes happened only at very specific values of the tax. We will see that these behaviors correspond to efficient extreme points of the Pareto set, and to every extreme point corresponds a tax interval so that any value of the tax in this interval leads to the behavior given by that same extreme point.

The outline of the paper is the following. In Section 2, we present the diet formulation problem considering the phosphorus excretion. The general form of the bi-criteria problem is presented, the geometric structure of its Pareto set is described, and we indicate methods to compute this set in Section 3. Finally, in Section 4, we present the pareto set for our original diet formulation problem and shows the effect of the taxation system on the behavior of a producer. The results presented in this paper, the behavior of the decision maker, can be applied to any linear bi-criteria problem.

Pig Diet Formulation

To illustrate the effect of a tax on the criteria, we consider the pig diet formulation problem considering not only the cost of the diet but also an environmental consideration such as the reduction phosphorus excretion [1]. One way to analyze this problem is to rewrite the problem as bicriteria problem. Hence the Pareto set indicates the effect of the reduction of phosphorus excretion on the cost of the diet. It also presents different behaviors for the producers associated to levels of taxation. This information is certainly useful for a decision maker which must choose a diet which decreases the excretion without being too expensive

Classical Model

The least cost diet problem, introduced in [2], is a classical linear programming problem [3-5]. A decision variable jx is assigned to each ingredient and represents the amount (in kg) of the thj ingredient per unit weight (1 kg) of the feed. Together, they form the decision vector

in our model. The model’s objective function is the diet cost. A vector of unit costs

must be minimized over the set of feasible diets denoted by S. The classic least cost animal diet formulation model is:

The constraints impose some bounds on the quantity of the different ingredients in the diet. For example, a unit of feed is produced (a 1 kg mix), expressed by the constraint

Some ingredients, or combinations of ingredients, can be imposed on the diet. These restrictions give rise to equality constraints (=) or inequality constraints (≥ or ≤). More specifically, to satisfy protein requirements, the following constraints are introduced for the L groups of amino acids contained in the ingredients. We set

where dig lj aa represents the amount of digestible amino acid l contained in a unit of ingredient j and bl*is the minimum amount of digestible amino acid l required. Finally, the diet must satisfy the digestible phosphorus requirements * bph given by

where dig j ph is the amount of digestible phosphorus contained in a unit of ingredient j .

Modelling of phosphorus excretion

Phosphorus excretion is directly related to the excess of phosphorus in the diet. Hence, we must establish the phosphorus content of the diet and consider the parts that is assimilated. The phosphorus content of a unit weight diet

of phosphorus which is digested. In this way the phosphorus excretion ( ) ph r x is given by the phosphorus content of the diet from which we remove the amount of phosphorus which is digested of phosphorus which is digested. In this way the phosphorus excretion ( ) ph r x is given by the phosphorus content of the diet from which we remove the amount of phosphorus which is digested

Hence, decreasing the phosphorus excretion ( ) ph r x is equivalent to decreasing the phosphorus content pr q xof the diet while maintained fixed the needs * ph b in phosphorus.

Bi-Criteria Problem: Cost and Phosphorus Excretion

Since we look for least cost diet while considering the phosphorus excretion, we have two conflicting criteria. The bicriteria linear model is then formulated as follows

For this problem, the Pareto curve will indicate the diet cost increase caused by a phosphorus excretion decrease. It will give us the taxation levels producing changes in the behavior of the producer.

Data

To illustrate the problem and the method we consider data that represent real situation [1]. The ingredients and their corresponding variables are described in (Table 1, Table 2) contains the entire model together with the values of the technical coefficients of the model.

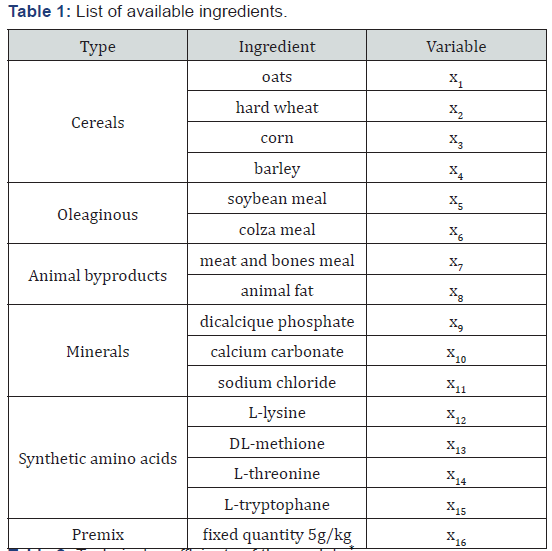
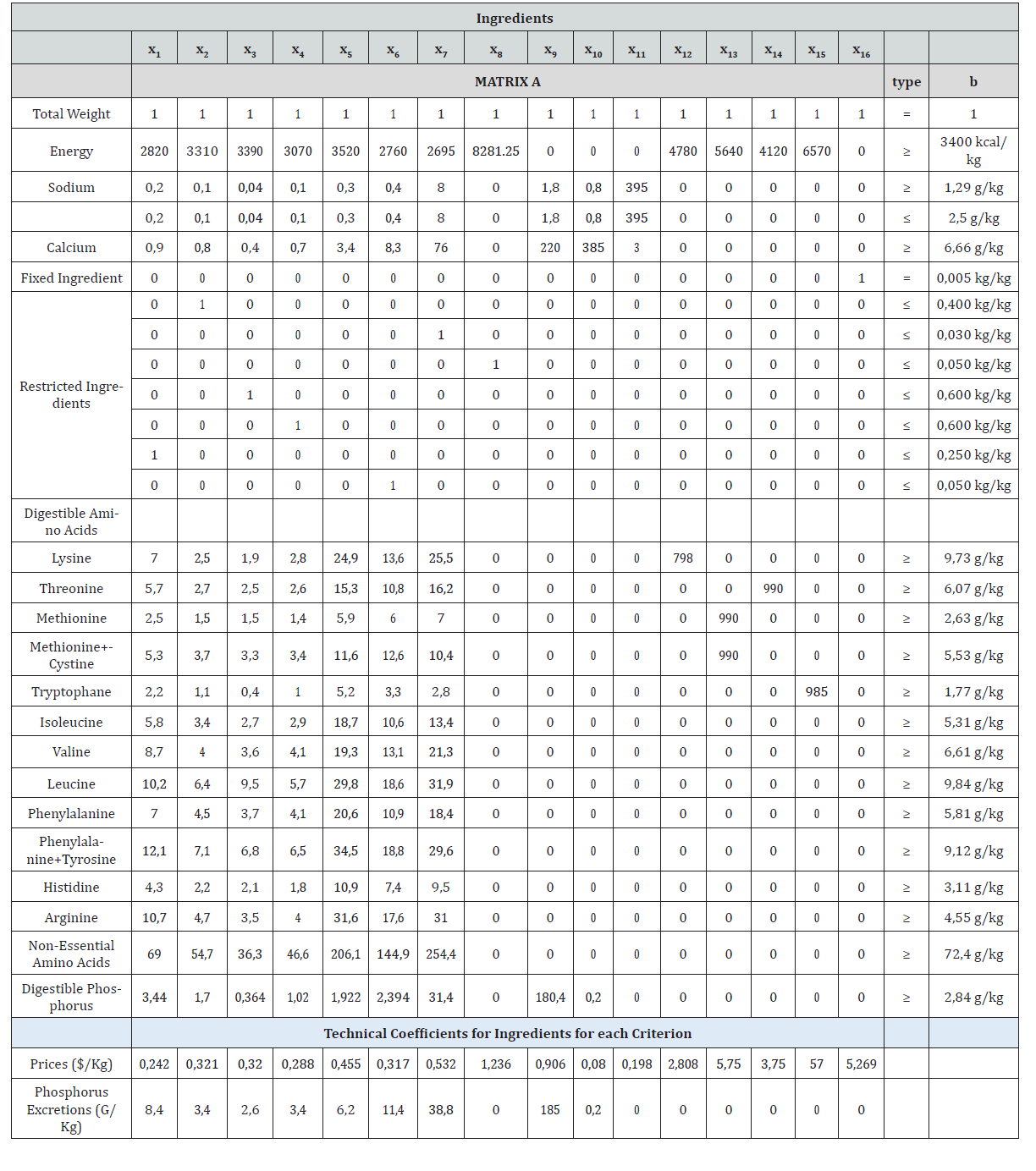
General Bi-Criteria Linear Program and its Pareto Set

In this section we present the general formulation of a bicriteria linear problem, and the main results on its Pareto set. We use the link with the parametric analysis to get information on the system of taxation and behavior of the decision maker.

Bi-Criteria linear programming problem

Let us consider the standard form of the bi-criteria linear programming problem [6].

where x is a column vector in n  , and they ' ( 1, 2) k c s k = are row vectors in n  . The feasible set S in n  is defined by S = {x∈n | Ax = b and x ≥ 0} , where A is a (m, n)-matrix, and b are a column vector in n  . Let C be the (2, n)-matrix given by

The feasible set in the criterion space 2  is then { 2 | for } . C X S = z∈ z = C x∈S = CS It is well-known that S and SC are polyhedral sets in n  and 2  respectively. Throughout this paper we will suppose that the two criteria are lower bounded on S which means that for i = 1, 2 we have

Pareto set

A feasible solution x∈s is an efficient solution if and only if it does not exist any other feasible solution x∈S such that

for at least one j∈{1,2}. The set of all efficient solutions is called the efficiency set noted ε , also called Pareto set. The corresponding set in the criterion space is the set c ε = cε

Geometric structure of the pareto set

Under the assumption that the two cost vectors c1 and c2 are linearly independent, and using weighted sums, we can replace the bicriteria linear programming problem by a single criterion linear programming problem. We consider λ ∈[0,1] and the weightedsum function is

Hence the efficiency set ε in the decision space is a connected set and is the union of faces, edges and vertices of S . This set may be quite complex due to the high dimension of the decision space. On the other side c ε , which is the image in 2  of ε by a linear transform, is a much simpler set.

Since we have assumed that both criteria are lower bounded on S , it follows that c ε is a simple compact polygonal line. Indeed, in that case c ε is the union of a finite number L of segments [ ]

To each segment is associated a weight l 1,l λ − such that the vector 1, 1, (1 , )t l l l l λ λ − − − is orthogonal to the segment [ ] 1 , l l Q Q − in 2  . To each point Q of c ε is associated an interval Λ(Q) defined by

With 0 0,... . l λl −λ > for l = L More mathematical details are given in [7].

Link to parametric analysis

The parametric analysis is based on the weighted sum given by

for μ∈[0, +∞),which can represent a tax on the second criteria. The value function in this case is defined by

We could consider the single criteria problem for μ ≥ 0

Since λ and μ are related by the formulae

to the efficient extreme points { } 0 Q L l l= on the efficiency set ε c we associate to these extreme points the following intervals for the parameter μ

In many applications, the parameter μ is in fact a taxe over the the second criteria (for a minimization problem). Interesting enough is to observe that the behavior (extreme point) change only for the critical values μl−1,l of the parameter μ. Indeed when μ increases and its value passes through μl−1,l , the behavior moves from the extreme point 1 Ql− to the extreme point l Q . Moreover, any level of taxes μ strictly between the values 1, l l l μ μ − = and μl,l+1 = μl gives the same behavior described by the extreme point l Q .

Software

Several methods exist for computing the Pareto set of a bicriteria linear program, for example [7,8]. We have developed our own method which requires only elementary results from a linear program solver [9]. It has been programmed in MATLAB and uses Linprog as the linear program solver.

Back to Pig Diet Formulation: Cost and phosphorus excretion

Let us come back to our bi-criteria linear model

Its two associated parametric models are

Its Pareto curve contains all the information for optimal decision considering the level of taxation. (Table 3) presents the efficient extreme points in the criterion space while the Pareto curve is sketched in (Figure 1). For this problem, the algorithm detects L = 22 segments and 23 extreme points. A total of 45 calls to a linear program software was required [9].

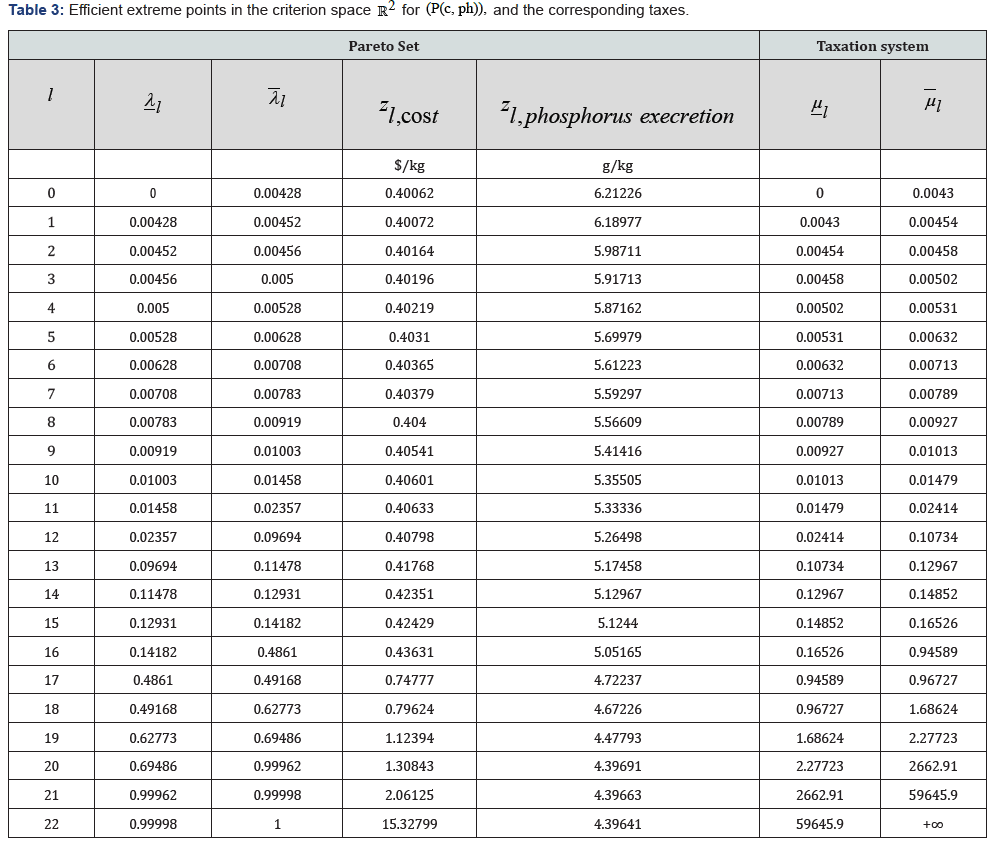
For each l , such that l = 0, . . . , 22, the extreme point Ql is given by

and corresponds to the optimal value of the criteria corresponding to any optimal solution of , (p ( )) c ph μ for any values of μ in ( , ) l l μ μ . So, the value function, with tax, is

as long as [ , ] l μ∈ μ μl . So, we see that for any tax value in [ , ] l l μ μ we will always have the same value function ϕ(μ ) , or the same behavior (zl,cost , zl,phosphorus execretion), and the change in the behavior will append only when the taxation level μ passes through the extremities l μ or l μ of this interval.

This is a nice example of abrupt (discrete) changes in behavior depending on the level of taxation of one criterion.