Estimation of DPT by Empirical and SVM-FA Models
Fatemeh Esmaeilbeiki1*, Bahar S Razavi2,3 and Parviz Zeaiean Firouzabadi 4
1Department of soil science and engineering. University of Tabriz, Iran
2Department of Agricultural Soil Science, University of Göttingen, Germany
3Institute of Plant Nutrition and Soil Science, Albrechtes-University of Kiel, Germany
4Department of Remote Sensing and GIS, Kharazmi University, Iran
Submission: October 27, 2018; Published: March 18, 2019
*Corresponding author: Fatemeh Esmaeilbeik, Department of soil science and engineering, University of Tabriz, Tabriz, Iran
How to cite this article: Fatemeh E, Bahar S R, Parviz Z F. Estimation of DPT by Empirical and SVM-FA Models. Agri Res& Tech: Open Access J. 2019; 20(3): 556132. DOI: 10.19080/ARTOAJ.2019.20.556132
Abstract
Dew Point Temperature (DPT) estimation is a critical issue in water stress managements. This study tries to investigate suitability and usefulness of a hybrid model of the firefly algorithm (FA) and support vector machine (SVM) techniques (SVM-FA) over two empirical models namely Magnus and Lawrence for prediction of DPT. To this end, daily DPT data measured during 2012 and 2015 at three climatic stations over Isfahan, Mashhad and Tabriz catchment areas located in Iran were used. The performance of SVM-FA model is evaluated in comparision of two empirical models. The results obtained in this study showed that in all three stations Lawrence model predicts DPT inaccurately. The DPTs were accurately estimated by SVM-FA hybrid model in three stations with RMSE values of 0.36, 0.55 and 0.22 for Isfahan, Mashhad and Tabriz station respectively. As SVM-FA shows the least error and the highest correlation coefficient (0.99), hybridization of support vector machine in Firefly algorithm has been successful. Furthermore, Lawrence experimental model results in the highest error and the lowest correlation coefficient (0.54). The results obtained indicated that the integration of SVM model with FA algorithm, gives better results than modeling with the SVM alone and empirical models. This study proved the suitability of the proposed SVM-FA model for DPT estimation.
Keywords: Empirical models; Firefly algorithm; Dew point; Hybrid model; Support vector machine
Abbreviations: DPT: Dew Point Temperature; FA: Firefly Algorithm; SVM: Support Vector Machine; WT: Wavelet Transform; ELM: Extreme Learning Machine; MAE: Mean Absolute Error; RMSE: Root Mean Square Errors
Introduction
Hypothermia and frostbite from the harmful effects environment generally occur suddenly and brings great harm to the agricultural economy. Damage both chilling and freezing phenomenon usually when there is a minimum (before sunrise) reaches its peak. The weather conditions and ambient temperatures are lower than the optimal temperature for growth [1,2]. When the frostbite occurred the plant tissues are strained, but not so cold that ice formation generally leads to the destruction of plant tissues. Although the effects of hypothermia differs between plant species when the air temperature is between 0 and 10 °C, unplanned stresses occur in the plants [1].
The temperature which the water in the air is distilled at a constant barometric pressure with the same evaporation rate it is defined as the dew point [3]. The temperature of the dew point is a temperature that the humid air needs to completely cool until it is saturated. Also, when the saturation pressure and the actual vapor pressure are alike, it is define as the thermal temperature [4]. In an arid environment, especially with infrequent precipitation the DPT would be actually vital for plant [5].
The meticulous DPT prediction would be of essential importance for a wide range of targets. DPT and relative humidity (RH) are usually used to identify the rate of air moisture. Moreover, it may be utilized in junction with the wet bulb-temperature for temperature calculation, which prevents frost and loss of product [5,6]. When moisture is low, the DPT becomes an important parameter for snow or rain forecasting. Mainly DPT with relative humidity is used to measure the amount of air moisture [7]. In many agricultural and hydrological models, the DPT for assessment of evaporation and evapotranspiration is necessary as a key input parameter [2]. Dew point is of great interest to meteorologists because it is a fundamental measure of the state of the atmosphere in terms of how much water vapor is present [8].
To estimate the next day’s low temperature as under certain conditions it will end up pretty close to the dew point at the time of maximum temperature the day before it will be a reliable and important starting point [5,8]. So far, many studies have been conducted to estimate the DPT [3,9-11] and to calculate the DPT relationships based on average air temperature and humidity by Magnus and Lawrence method [7,12]. In the past years, with the entering of artificial intelligence models into sciences such as agriculture and meteorology, use of model such as support vector machine applied to estimate the DPT [13]. Hamidi et al. [14] modeled monthly rainfall in Hamedan, Iran in an efficient way using SVM and ANN methods. More accurate outputs have been achieved via SVM method, with. Demonstrated superior efficiency in comparison to the ANN method. Therefore, SVM was famous as an effective method for rainfall modeling. Shiri et al. [10] applied GEP and ANN algorithms to estimate DPT with 8 years daily dataset of a couple of climatic stations located in Korea. The dataset includes wind speed, down welling solar energy, temperature, pressure, RH, and DPT. They concluded that the GEP is better than ANN for prediction of daily values of DPT [10]. Amirmojadedi et al. [15], used a hybrid model of wavelet transform (WT) and extreme learning machine (ELM), called ELM-WT for the estimation of the daily DPT average air temperature, RH and atmospheric pressure, pertaining to the south coastal of Iran were considered as input elements. They reported that their proposed hybrid model is able to outperform other examined techniques. Although, qualification of a model for prediction of DPT is of point of interest in agro-ecosystem [15].
In this study we aimed to predict DPT through support vector machine and integration with hybrid Firefly algorithm.one of the most important algorithms to determine the optimal parameters of support vector machine is the Firefly algorithm (FFA). Although Firefly algorithm (FA) has been used successfully in different fields, but the most appropriate result obtained for the DPT estimation. For the reason to demonstrate the compatibility of the hybrid SVM-FA approach, its performance is compared with the SVM and empirical techniques (Lawrence and Magnus). Three stations located in north of Iran was selected as a case study and daily DPT data sets from three climatic stations during 2012-2015 years over the catchment were utilized.
Materials and Methods
Study area and dataset
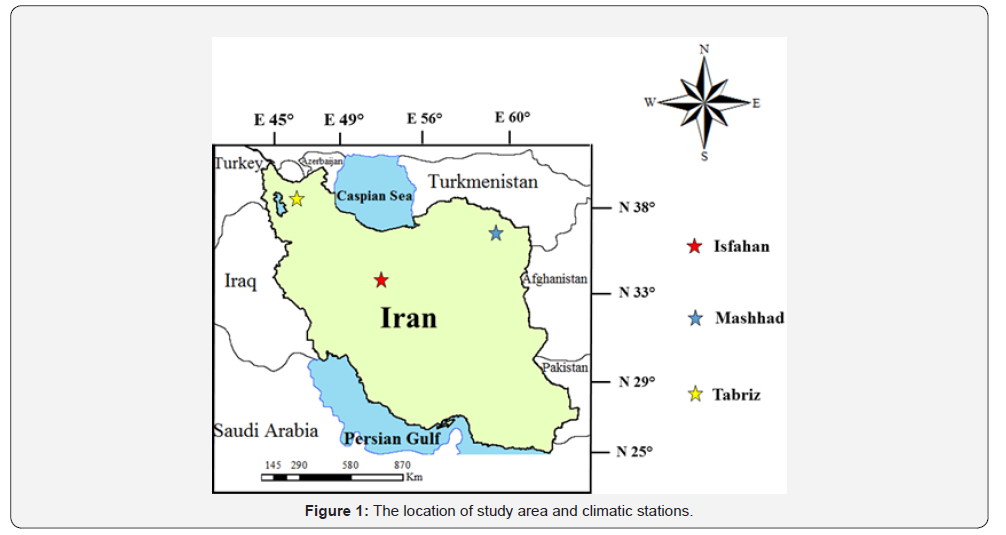
Methods
The methodology adopted in this research work is shown Figure 2. All collected data were corrected for their probable gaps or missing measurements through statistical analysis. Results are shown in Table 2. DPT modelling is performed through different algorithms discussed earlier in previous section. For the reason of evaluation of the models, mean absolute error (MAE), the Nash– Sutcliffe coefficient, and root mean square errors (RMSE), have been used. A brief description of scientific background of SVM, firefly algorithms and empirical methods used to estimate DPT is provided in the following sections.
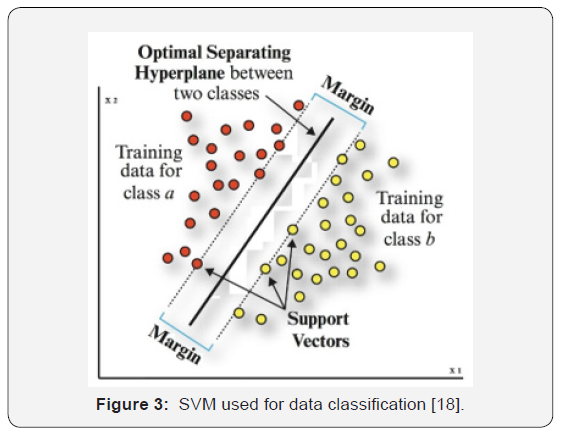
Support vector machines (SVM): Support vector machines is a set of supervised learning methods used for classification and regression analysis. Introduced by Chervonenkis in 1971 and founded upon statistical learning theory, this method is based on dual classification in the arbitrary feature space and hence is well-suited for prediction problems [16,17]. It is an efficient learning system based on constrained optimization theory, which uses the inductive principle of structural risk minimization and leads to an overall optimal solution. The SVM structure is shown in Figure 3 [18]. To implement this algorithm on present data, a program named Support Vector Machines was developed in MATLAB environment package [19].

Firefly algorithm: Xin-She Yang [20] introduced the fundamental behind firefly algorithm. Different steps involved in this algorithm have been summarized by Tighzert et al. [21] as follows [21,22]:
a. Brightness: presenting the distance between the atmospheric absorption coefficient and fireflies calculated as:
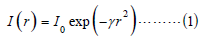

Where I is the intensity of the light, ɣ is the absorption coefficient, r is the distance between the two fireflies and 0 I is the intensity of the light source when r = 0.
b. Attractiveness: it can be expressed by:

Where 0 þ is the attractiveness of the firefly when r = 0.
The moving step, for the entire population and for each pair of fireflies, the less fit firefly is moved toward the cost-efficient ones, using the following model:
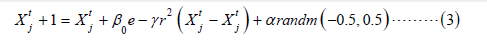
Where α is the mutation coefficient which is generally a self-adaptive parameter decreasing through iterations and randm (−0.5, 0.5) is a normal randomized number between [−0.5, 0.5].
Empirical methods: Two important climatic parameters, the RH and ambient temperature are the bases for the empirical methods. The DPT, the temperature of the cooling needs due to water vapor in the air condenses out as dew point on surfaces. While there are many ways in which to estimate the DPT, Lawrence with RH [7] derived this formula based on the empirical formula by Magnus [23].
Lawrence: Indicators that, the amount of moisture in the air to estimate are, the RH (RH) and the DPT (td) [7].
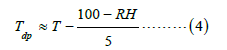
Where t and td are in degrees Celsius and RH is in percent.
Magnus: Equations 5 and 6 shows the relationship between saturation vapor pressure over water or ice as a function of absolute temperature [23];
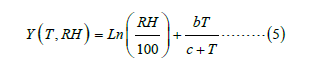
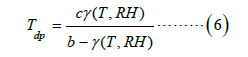
This is known as Magnus formula. α= 6.112 milliard; b= 17.67; c= 243.5 ˚C
Performance criteria
In order to evaluate the models for the effectiveness of fit, the fallowing two statistical indicators are used:
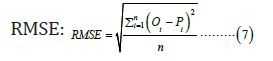


Where n is the total number of data; and i O and i P are the observed and predicted DPT data, respectively.
Taylor diagrams: To understand the behavior of two data sets graphically in respect to their correlation coefficient, standard deviation and RMSE Taylor diagrams are used. Taylor diagrams have primarily been used to evaluate models designed to study climate and other aspects of Earth’s environment [24]. In such mathematical diagrams the goodness of data produced by different models are compared to observations data set. Taylor graph is for a set of points is dispersed on a polar plot designed to graphically indicate which of several approximate representations (or models) of a system, process, or phenomenon is most realistic. In Taylor representation, the correlation coefficient between the predicted and observed data is shown by an azimuth angle. Radial distance from the origin represents the ratio of the normalized standard deviation (SD) of the simulation to that of the observation.
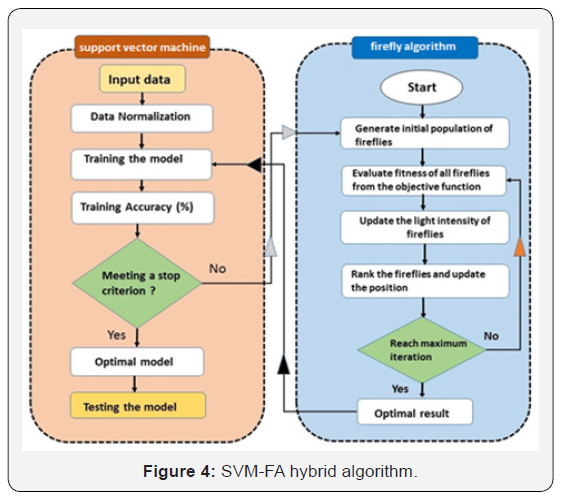
VM-FFA hybrid model: Here, to determine the optimal parameters for support vector machine a FFA model is used. Figure 4 indicates how the designed strategy (i.e. hybrid SVM-FFA model) does this in practice. A toolbox has been developed as an interface to connect SVM script to FFA program in Matlab environment.
Results and Discussion
In this study, for evaluating the models performances two different combinations of average air temperature and RH were considered as the models inputs (Table 1).
Results of implementing the SVM model
There are two basic steps for significance of SVM model:
a. The choice of the kernel function.
b. The recognition of the particular parameters of the kernel function, i.e. ∁ and ε. In this research using radial basis functions (RBF) and three function. ∁, ε, and γ was done. The RMSE criterion was used to obtain optimal values of these parameters. The results indicated that the SVM model with kernel parameters values (γ) of 54.25 (Isfahan), 75.06 (Mashhad) and 66.82 (Tabriz) performs successfully. According to Table 3, the SVM model estimates DPT more or less precisely for three stations.
The SVM-FA model
In the SVM-FA hybrid model, the optimal values of the SVM parameters were determined using the Firefly Algorithm. Figure 5, shows schematically input and output form in the hybrid model. The results indicated that the optimal parameters of the SVM model determined by the FA are equal to 32.04, 48.12 and 36.54 for Isfahan, Mashhad and Tabriz respectively.
Comparison of the models
The Table 2 includes the performances of the SVM, Lawrence, SVM-FA and Magnus models and compares them using the statis tical measures. Accordingly, the performance of all the methods is acceptable for DPT estimation. However, accuracy of the SVM-FA model is significantly higher than the SVM, Lawrence and Magnus models. This proves the high ability of the FA optimization algorithm in calibrating the SVM model. The SVM technique performs similarly and there is not significantly difference between their accuracy of simulating based on values of the statistical measures. However, the SVM-FA model indicates some more ability than the SVM, Lawrence and Magnus in DPT estimation. This is because of higher accuracy according to Table 3.


In Isfahan site, between SVM, SVM-FA, the best smart model was SVM with test data RMSE of 0.36 ˚C. Besides, with test data RMSE of 1.38 ˚C, Magnus was the best experimental model, compared to Lawrence. However, in Mashhad site the best model was SVM-FA with test data RMSE of 0.55 ˚C and, the best experimental model was Magnus with test data RMES of 1.64 ˚C. In addition to that, the best model was SVM-FA with test data RMSE of 0.22 ˚C in Tabriz site, while the best experimental model was Magnus with test data RMES of 1.35 ˚C.
Scatter diagram of the points that have been observed and estimated by the models in Isfahan site is shown in Figure 6. On the whole, artificial intelligence models have been more successful than experimental ones. Concurrently, correlation coefficient of Magnus experimental model is significantly close to SVM artificial intelligence model. As SVM-FA shows the least error and the highest correlation coefficient (0.99), hybridization of support vector machine in Firefly algorithm has been successful. Furthermore, Lawrence experimental model results in the highest error and the lowest correlation coefficient (0.54).


The same diagram of observed and estimated points in Mashhad site is depicted in Figure 7. It can be seen that; SVM-FA model shows the highest correlation coefficient which is 0.99. Furthermore, the Lawrence model with correlation coefficient of 0.56 has the lowest correlation coefficient among all utilized models. Despite the other sites, correlation coefficient of Magnus experimental model in Mashhad is 0.97. It is higher than smart model of SVM, which is 0.96. It can be a sign of the compatibility of a, b and c factors in Magnus equations (Eq.5 and 6) with Mashhad site’s climate in dew point evaluation.
Moreover, scatter diagram of observed and estimated values in Tabriz site shows that SVM-FA, SVM, Magnus and Lawrence have been able to estimate dew point with correlation coefficient of 0.99, 0.985, 0.98 and 0.82, in respect (Figure 8).

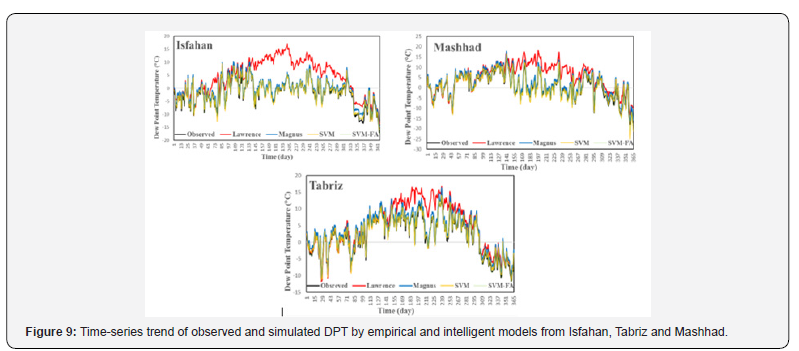
Time-series of dew point estimated values, in comparison with observed values, shows that, in all 3 sites Lawrence model has the largest deviation from observed values (Figure 9). However, deviation from Lawrence model observed mainly during autumn. According to the equation (9), Lawrence model has direct correlation with RH and is affected by humidity which suggests that such deviation in autumn is due to higher RH. This indicates that Lawrence is not the appropriate model for prediction of DPT in autumn or any regions with high relative moisture e.g. tropics.
SVM-FA shows the best fitness with observed values. It indicates a better performance of the SVM-FA model in dew point evaluation. Magnus and SVM models had adequate performance so that they show slight deviation from observed values. They had poor performance in comparison with SVM-FA model, though.
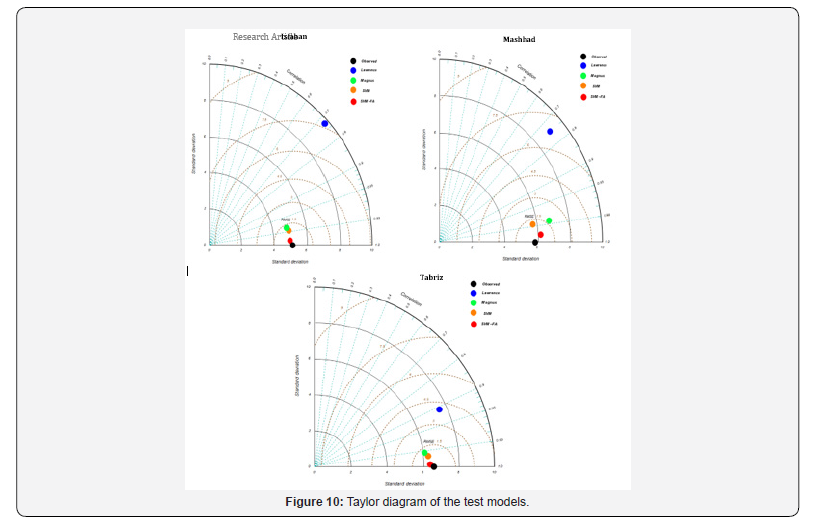
Taylor diagrams were plotted for all three stations (Figure 10). In this diagram each model that is closer to the observation point has higher accuracy, and the one that is far from the point of observation is a weaker model. While for all three stations nearest point to the reference model is. SVM-FA and the far point is Lawrence. Thus, SVM-FA is the best model and Lawrence model is the weakest. The other two models Magnus and SVM are very close to each other and SVM model is superior to Magnus by a small margin.
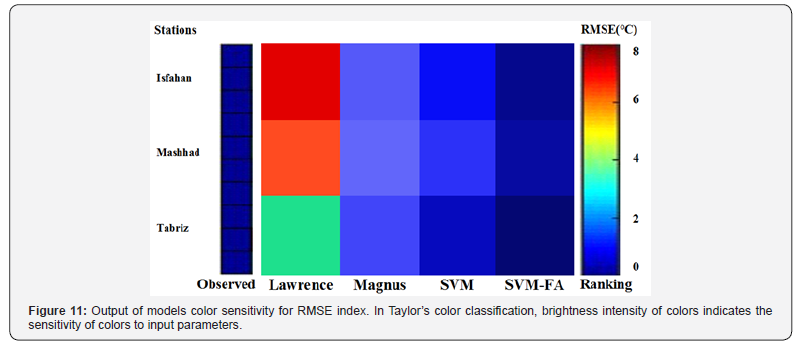
Finally, Taylor diagram was used to show the intensity of output sensitivity to Mean Squared Error criterion (Figure 11). In Taylor’s color classification, brightness intensity of colors indicates the sensitivity of colors to input parameters. In Figure 11, which is related to the Taylor classification of the test data at three stations in Isfahan, Mashhad and Tabriz, it is observed that in the SVM-FA, SVM and Magnus models, the color change rate is horizontally lower than each other and the colors which are more homogenous and closer, have more similar results, suggesting that SVM-FA, SVM and Magnus models have similar results and have almost the same behavior in DPT modeling. Studying the change rate of colors vertically for three mentioned models shows that Isfahan and Tabriz stations have behaved exactly the same; this fact is related to the climate of these stations indicating that SVMFA, SVM and Magnus models have exactly the same behavior in Isfahan and Tabriz stations. The results of Lawrence model show that this model has different colors than other models which indicate that the results of this model are very different from other ones. Generally, the results of Lawrence model were weaker than the other three models. The results of this model were better at Tabriz than Mashhad and Isfahan stations. The results were much weaker in Isfahan.
Conclusion
Altogether, in this study, performances of the new hybrid SVMFA model were evaluated for DPT estimation and compared with the SVM, Lawrence and Magnus in the three catchments in Iran. In SVM-FA model, the FA algorithm was used to determine the optimal parameters of the SVM. As it was expected, the results showed successful performance of the SVM-FA model compared to the SVM, Lawrence and Magnus for DPT modeling.
The results showed that in all three stations Lawrence model accurately predicts little DPT as well as model SVM-FA have three stations with the highest DPT accuracy of the estimate, RMSE values respectively related to the testing station in Isfahan, Mashhad and Tabriz to 0.36, 0.55 and 0.22, respectively. Thus, certainly the hybrid algorithm (SVM-FA) in all three stations was qualified as “Best Model”. Overall the relative air humidity, DPT and the average temperature smart models are more successful than experimental models. Combining firefly algorithm with vector machine model has been successful and SVM-FA hybrid model could accurately estimate the DPT.
Utilizing Firefly optimization algorithm and its combination with artificial intelligence estimators can improve the accuracy of the results of modeling. By taking into consideration the importance of dew point in environmental planning and management, employing SVM-FA model, which has higher accuracy in dew point estimation, is suggested as a replacement for experimental models.
Finally, we conclude that;
a. Integration of Firefly algorithm and support-vector machine is an appropriate tool to estimate dew point, so that Firefly- hybrid algorithm (SVM-FA) is more successful than vector machine, and Magnus and Lawrence experimental models.
b. In all 3 sites (Isfahan, Mashhad and Tabriz) SVM-FA is the superior model and Lawrence is the inferior one.
References
- Levitt J (1980) Responses of Plants to Environmental Stress, Volume 1: Chilling, Freezing, and High Temperature Stresses, Academic Press, New York, pp. 698.
- Hubbard KG, Mahmood R, Carlson C (2003) Estimating daily dew point temperature for the northern Great Plains using maximum and minimum temperature. Agronomy Journal 95(2): 323-328.
- Arabloo M, Shokrollahi A, Gharagheizi F, Mohammadi AH (2013) Toward a predictive model for estimating dew point pressure in gas condensate systems. Fuel processing technology 116: 317-324.
- Yousif TA, Tahir HM (2010) The Relationship between Relative Humidity and the Dew point Temperature in Khartoum State, Sudan. Journal of Applied and Industrial Sciences 1(5): 20-23.
- Agam N, Berliner P (2006) Dew formation and water vapor adsorption in semi-arid environments-a review. Journal of Arid Environments 65(4): 572-590.
- Snyder RL, de Melo-Abreu JP (2005) Frost protection: fundamentals, practice and economics. Environment and Natural Resources Series 10.
- Lawrence MG (2005) The relationship between relative humidity and the dewpoint temperature in moist air: A simple conversion and applications. Bulletin of the American Meteorological Society 86(2): 225- 233.
- Ali J, SS (2015) Dew point temperature modelling by using Artificial Neural Network and Multiple Linear Regression Technique. International Journal of Agricultural and Food Science 5: 125-133.
- Mahmood R, Hubbard KG (2005) Assessing bias in evapotranspiration and soil moisture estimates due to the use of modeled solar radiation and dew point temperature data. Agricultural and forest meteorology 130(1-2): 71-84.
- Shiri J, Kim S, Kisi O (2014) Estimation of daily dew point temperature using genetic programming and neural networks approaches. Hydrology Research 45(2): 165-181.
- Baghban A, Bahadori M, Rozyn J, Lee M, Abbas A, et al. (2016) Estimation of air dew point temperature using computational intelligence schemes. Applied thermal engineering 93: 1043-1052.
- Bolton D (1980) The computation of equivalent potential temperature. Monthly weather review 108(7): 1046-1053.
- Mohammadi K, Shamshirband S, Motamedi S, Petković D, Hashim R, et al. (2015) Extreme learning machine-based prediction of daily dew point temperature. Computers and Electronics in Agriculture 117: 214- 225.
- Hamidi O, Poorolajal J, Sadeghifar M, Abbasi H, Maryanaji Z, et al. (2015) A comparative study of support vector machines and artificial neural networks for predicting precipitation in Iran. Theoretical and applied climatology 119(3-4): 723-731.
- Amirmojahedi M, Mohammadi K, Shamshirband S, Danesh AS, Mostafaeipour A, et al. (2016) A hybrid computational intelligence method for predicting dew point temperature. Environmental Earth Sciences 75: 415.
- Vapnik V (2000) The nature of statistical learning theory. Springer New York Google Scholar.
- Vapnik V, Golowich SE, Smola AJ (1996) Support vector method for function approximation, regression estimation and signal processing. Advances in neural information processing systems.
- Meyer D (2014) Support vector machines.
- Math Works I (2012) Matlab the language of technical computing.
- Yang XS (2008) Introduction to mathematical optimization. From Linear Programming to Metaheuristics.
- Tighzert L, Fonlupt C, Mendil B (2017) A set of new compact firefly algorithms. Swarm and Evolutionary Computation 40: 92-115.
- Yang XS (2010) Firefly algorithm, stochastic test functions and design optimisation. International Journal of Bio-Inspired Computation 2(2): 78-84.
- Magnus G (1844) Versuche über die Spannkräfte des Wasserdampfs. Annalen der Physik 137(2): 225-247.
- Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysical Research: Atmospheres 106(D7): 7183-7192.






























