The Study Contact Bending Stress Two-Layer Plates from Fiberglass with Interfacial Defects of Structure
Emad Toma Bane Karash*
Northern Technical University, Iraq
Submission: September 09, 2017; Published: October 16, 2017
*Correspondence author: Emad Toma Bane Karash, Northern Technical University, Iraq, Email: Emadbane2007@yahoo.com
How to cite this article: Emad T. The Study Contact Bending Stress Two-Layer Plates from Fiberglass with Interfacial Defects of Structure. Agri Res & Tech: Open Access J. 2017; 12(1): 555834. DOI: 10.19080/ARTOAJ.2017.12.555834
Abstract
The presented version of the nonlinear discrete-structural theory adequately reflects the work of real structures. Obtained are in satisfactory compliance with the theoretical and experimental data. The magnitude of the transverse shear stresses of contact increases 4-5 times in a zone bearing the circuit, which leads to interfacial failure of the adhesive layer Thus, the proposed model allows the calculation to locate the contact area, touch, pressure, and the changing nature of the state stress at the interface.
Keywords: Structure; Bending stress; Fiberglass; Anisotropic; Shell
Introduction
The significant difference between mechanical and physicalproperties of the individual components of the structure of layered thin-walled structural elements have driven to the creation of adequate discrete-structural theories to calculate this group of problems. Contact problem of mechanics of multilayered plates and shells is considered in [1-6], which, based on the discrete approach built functional and obtained a system of equations for solving such problems, provided non-ideal contact layers. A method for solving nonlinear problems of contact between the two shells of different shapes and equidistant layers can be found in [7-10], on the other handdetailed analysis of the latest results and trends in the development of the discrete- structural theory of laminated plates and shells found in [11].
In this paper, we propose a variant of the geometrically nonlinear dispersion specifically-layered structure theory of structural elements and study nature of the change of contact stresses in bending double-layer plates fiberglass with interfacial defects of the material structure. The derivation equilibrium equations and geometric ratio take into account the influence of transverse shear deformation and compression. The results of theoretical studies are compared with experimental data.
Formulation of Analytical Model
According to the theory of discrete structural, mathematical model considered, the multilayer shell consists of n thin anisotropic layers. The volume of (n) rigid layers is 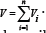 .Each cladding layer undeformed assigned to an orthogonal curvilinear coordinate system,
.Each cladding layer undeformed assigned to an orthogonal curvilinear coordinate system, 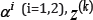 Coordinate directed along the common normal
Coordinate directed along the common normal 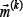 to the middle surface S(k) and equidistant surface S(k)z k-th layer. Index "z" with the introduction of other characters means that the corresponding values are to the point (α1,α2,z(k))equidistant surface S(k)z
to the middle surface S(k) and equidistant surface S(k)z k-th layer. Index "z" with the introduction of other characters means that the corresponding values are to the point (α1,α2,z(k))equidistant surface S(k)z
Total displacement vector 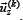 k-th point of the hard layer according to the refined Tomachinko shell theory can be represented as:
k-th point of the hard layer according to the refined Tomachinko shell theory can be represented as:
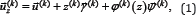
Where 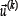 displacement vector points of the middle surface
displacement vector points of the middle surface 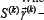 Vector function of the angles of rotation and compression of the fibers in the direction normal to the undeformed middle surface S(k) during deformation.
Vector function of the angles of rotation and compression of the fibers in the direction normal to the undeformed middle surface S(k) during deformation.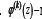 Nonlinear continuous distribution function tangential displacements through the thickness of the k-th layer, analysis and approximation given in [11]
Nonlinear continuous distribution function tangential displacements through the thickness of the k-th layer, analysis and approximation given in [11]
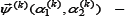
Vector shift function. Covariant components of vectors 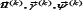 recorded using the following expressions:
recorded using the following expressions:
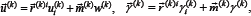

Deformation tensor components (α1,α2,z(k)) defined as half the corresponding metric tensor components before and after deformation:

The finals of the equilibrium equations and boundary conditions for the solution of contact problems of laminated shells are usually made on the basis of Reissner variational principle. Considering that in the direction normal to the middle surface of the individual layers of the shell axial line of general and topical coordinate systems are combined and also bias with the topical coordinate sursurfaces of the middle surface Layers, the variational equation for the Reissner principle multilayer shell write in the following format:

Punctuation starts from the layers of negative values of zfrom 1 to n. Wherein F(k) - specific additional work strain k-th layer,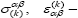 components of the stress and the strain tensors.
components of the stress and the strain tensors.
If we assume that the dual sursurfaces of the k-th layer of the conditions of full contact:
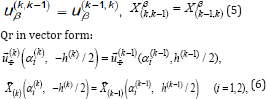
The difference of the elementary work of external forces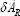 represented by the following formula:
represented by the following formula:

WhereS(k) - middle surface of the k-th layer;  part of the loop,l(k) Vectors external forces
part of the loop,l(k) Vectors external forces  moments
moments  and additional points
and additional points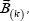 are inclusive in the equation (7), are defined by:
are inclusive in the equation (7), are defined by:
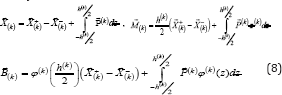
Where the vectors 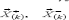 include the contravariant components of the tensor of contact stresses :
include the contravariant components of the tensor of contact stresses :
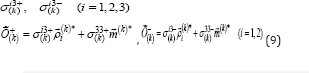
Subscripts "+" and "- " indicate the top and bottom surfaces of the k-th layer A similar entry are vectors of the external load  :
:
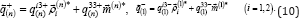
Vector 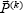 takes into account the effect of its own weight. contravariant components
takes into account the effect of its own weight. contravariant components 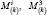 vector moment
vector moment 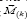 with respect to the basis vectors
with respect to the basis vectors  as to the equation:
as to the equation:
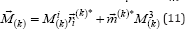
Also, elementary work (7) the layer ofthe shell is differentiated mainly by the vector 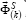 the main point
the main point 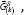 additional main point
additional main point 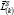 that arise from the action of the external forces on the contour
that arise from the action of the external forces on the contour 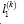 main vector
main vector 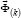 the main point
the main point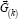 additional main point
additional main point 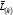 associated with the tension at loop
associated with the tension at loop 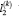 by virtue of a predetermined displacement of the contour points
by virtue of a predetermined displacement of the contour points 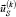 .
.
The second term of equation (4) should be represented in the form:
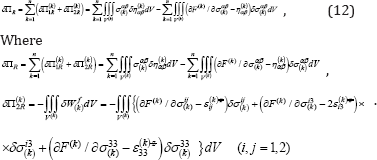
And offset equations (3) (4), (7), (12) and varying the mutually independent displacements and stresses can be obtained for each individual cladding layer system of equilibrium equations, physical relationships, static and kinematic boundary conditions. Application of the generalized Hooke's law, the nonlinear theory of the average bending diaphragm [12] simplifies the derivation of the equilibrium equations and boundary conditions. The transition to the physical components used in this study tensors, the inference of the equilibrium equations and boundary conditions can be found in [13].
For a rotating shell which comprises n layers of coaxial sursurfaces of revolution, the solution of partial differential equations is as follows:
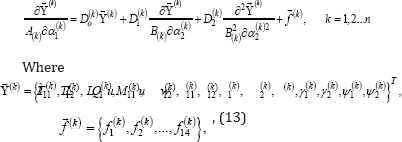
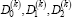 - Square matrices 14th. The main unknown function occupies a valuethat define the boundary conditions on the lateral contour of the k-th layer denotedshell. Due to the lack ofspace to show resolution systemequations, physical and geometrical ratio in developed formis notpossible.Kinematic and static contact condition (5) facial surfacek-th layer and associated sursurfaces,k + 1 and k - 1-th layer, according to the notation introduced earlier take this equation:
- Square matrices 14th. The main unknown function occupies a valuethat define the boundary conditions on the lateral contour of the k-th layer denotedshell. Due to the lack ofspace to show resolution systemequations, physical and geometrical ratio in developed formis notpossible.Kinematic and static contact condition (5) facial surfacek-th layer and associated sursurfaces,k + 1 and k - 1-th layer, according to the notation introduced earlier take this equation:
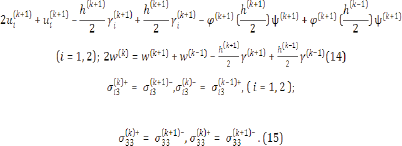
Presented the kinematic relations (14) in the construction of resolving a system of equations (13) for the entire package element layers and proceed static conditions on personal contact mating sursurfaces (15) on the basis of the penalty function method [11], we can create an algorithm for solving the contact problem discrete structural theory of multilayer shells. If between k-th and k + 1-th cladding layers. Assuming no kinematic connections at the surface interface of these layers may occur effort unknown vectors  contact interaction. According to the 3rd Newton's second law is a dependence
contact interaction. According to the 3rd Newton's second law is a dependence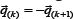 To account for the impact of the efforts of the contact interaction of the layers in the variational equation Reissner principle (4) it is necessary to introduce a term that takes into account the work force of contact interaction in the motion vector of each layer portion of the mating surface:
To account for the impact of the efforts of the contact interaction of the layers in the variational equation Reissner principle (4) it is necessary to introduce a term that takes into account the work force of contact interaction in the motion vector of each layer portion of the mating surface:
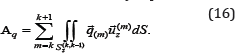
Efforts contact interaction 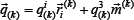 arise when the condition
arise when the condition
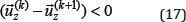
Coupling in areas harsh layers, in the case, where the inequality (17) is not performed while moving the field of points  during deformation, the contact pressure
during deformation, the contact pressure 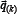 in equation (13) takes the value
in equation (13) takes the value 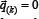 .Solving the system of equations (13), it is easy to find the value of a given accuracy of the contact pressure on the basis of the iterative method suggested in [12].
.Solving the system of equations (13), it is easy to find the value of a given accuracy of the contact pressure on the basis of the iterative method suggested in [12].
Results and Discussion
Test cases investigated plate round shape in terms of diameter 0.16m regular structure of fiberglass. Considered plates were made of 4 - layers of glass TG 430 - C (100) (producer - Latvia). The binder used polyester orthophthalic resin with low styrene emission Cristic 2 - 446PA (producer - UK). Physical and mechanical properties of fiberglass plates determinedmined as follows. Initially, according to GOST 25,601- 80, determined by the elastic modulus and Poisson's ratio when stretchingthe sample is made of fiberglass. Therefore mechanical testingmakes it possible to assert that the records can be considered material class-classify as a transversely isotropic (E11 = E22 = 1.5 • 104 MPα,v12 = v21 = 0.12). The remainder of the physical and mechanical characteristics of black glass-stick determined by the integral over the entire packet layers of the plate on the basis ofdependencies work [12].
when the elastic moduli ofthe 1st kind, the coefficientsPoisson fibers and the matrix are respectively equal to: EB = 7.0 • 104 MPα;EM = 3.5 • 103 MPα; vB = 0.22; vM = 0.35. The deflection of the plate was measured using dial gaugesup to 0.01 mm. To measure the strain gage used KF4P1-3-200. Sticker gages carried out according to the instructions on the label AZHV TO 2,782,001. To measure the output signals of strain gages and reporting digitally measuring system used SIIT-3.A mathematical model of calculation is a two-layer planSteen composed of two layers of thick hard transtropich (1) = h (2) = 1.0 x 10-3 m.
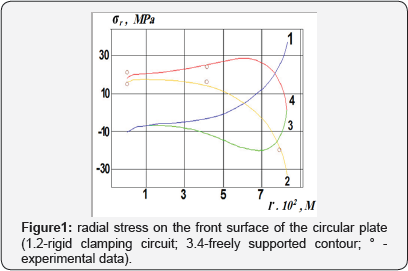
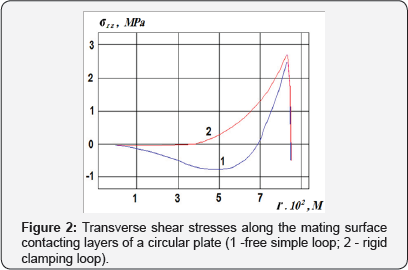
It is presumed that the interfacial contact area of the hard layer is very pliable, that is, they may be "slippage" relative to each other.The results of studies of plate bending under the action of uniform pressureq = 0.025 Mpα are shown in Figure 1-2. The relative error of the theoretical value of the deflection in the center of the plate, when compared with the experimental data was less than 3%: wz = 0.2. 10-2 m - A rigid clamping circuit; ws = 0.2.10-2m - for a simply supported contour
Conclusion
According to thenonlinear discrete - structural theory of multi-layer plates and shells the intense deformed case of anisotropic elements with defects in the structure of the material is investigated. At the conclusion of the equations of balance and geometrical parity the influence of deformations of cross shift and cross-pressure is taken into account. The results of theoretical research are compared with experimental data.
Acknowledgment
This research was supported by Mechanical Engineering Research Program in the Northern Technical University/ Technical Institute of Mosul funded by the Ministry of Higher Education and Scientific/Research/Republic of Iraq. (No. 201600432).
References
- Brischetto S, Carrera E (2010) Coupled thermo-mechanical analysis of one-layered and multilayered plates. Composite Structures 92: 17931812.
- Carrera E, Brischetto S (2010) Thermo-mechanical coupling in multilayered plates and shells. 27th international congress of the aeronautical sciences, pp. 1-10.
- Guidault PA, Allix O, Champaney L, Navarro JP (2007) A two-scale approach with homogenization for the computation of cracked structures. Computers & Structures 85(17-18): 1360-1371.
- Kim JS Cho M (2007) Enhanced first-order theory based on the mixed formulation and transverse normal effect. International Journal of Solids and Structures 44: 1256-1276.
- Cen S, Long Y, Yao Z (2002) A new hybrid enhanced displacement based element for the analysis of laminated composite plates. Computers & Structures 80(9-10): 819-833.
- Wang X, Zhong Z (2003) Three-Dimensional Solution of Smart Laminated Anisotropic Circular Cylindrical Shells with Imperfect Bonding. International Journal of Solids and Structures 40(22): 59015921.
- Yu B, Yang L (2010) Elastic Modulus Reduction Method for Limit Analysis of Thin Plate and Shell Structures. Thin-Walled Structures 48(4-5): 291-298.
- Rahman T, Jansen EL (2010) Finite Element Based Coupled Mode Initial Post-Buckling Analysis of a Composite Cylindrical Shell. Thin- Walled Structures 48(1): 25-32.
- Sofiyev AH (2003) Torsional Buckling of Cross-Ply Laminated Orthotropic Composite Cylindrical Shells Subject to Dynamic Loading. European Journal of Mechanics 22(6): 943-951.
- Li ZM, Lin ZQ (2010) Non-Linear Buckling and Post buckling of Shear Deformable Anisotropic Laminated Cylindrical Shell Subjected to Varying External Pressure Loads. Composite Structures 92(2): 553567.
- Zurich E (2008) Model for Interlinear Normal Stresses in Doubly Curved Laminates. International Journal of Mechanical Sciences, DISS. ETH NO. 17725.
- Fagiano C, Abdalla MM, Kassapoglou C, Gurdal Z (2011) Interlaminar Stress Recovery for Three-Dimensional Finite Elements.
- Xiang X, Guoyong J, Wanyou Li (2014) A numerical solution for vibration analysis of composite laminated conical, cylindrical shell and annular plate structures. Composite Structures 111: 20-30.






























