Mathematical Modeling of the Linear Stationary Process of Drying with Accuracy of Evaporation and Temperature Relation on the Surface of the Layer in Infrared Heating
Jasur S*, Shaxnoza S and Gani D
Tashkent State Technical University, Uzbekistan
Submission: July 28, 2017; Published: August 22, 2017
*Corresponding author: Jasur S, Tashkent State Technical University, Tashkent 100095, Republic of Uzbekistan, Email: jasursafarov@yahoo.com
How to cite this article: Jasur S, Shaxnoza S, Gani D. Mathematical Modeling of the Linear Stationary Process of Drying with Accuracy of Evaporation and Temperature Relation on the Surface of the Layer in Infrared Heating. Agri Res & Tech: Open Access J. 2017; 9(5): 555774. DOI: 10.19080/ARTOAJ.2017.09.555774
Abstract
The interaction of surface evaporation and the movement of moisture in the inner layers together with changes in the temperature field is a well-known task. In this paper, explicit finite formulas are obtained the behavior of this system under infrared irradiation for stationary problems. The obtained results of the interaction of the temperature field and the humidity field against the background of the irradiation surface by infrared rays.
Keywords: Drying process; Model; Infrared heating; Temperature; Evaporation
Introduction
At certain stages of drying, there comes a period for the stationary of drying processes, this is due to the fact that the thin time layer of moisture and temperature transition is small compared to the total drying time [1,2].
It is known that the boundary conditions on the surface of the dewatered material are complex, since the surface temperature and the moisture concentration on the surface with increasing their value increase the evaporation process [3,4]. On the other hand, surface evaporation, by lowering the temperature and humidity of a thin layer of the surface, affects the internal processes of redistribution of humidity and temperature [1-4]. In known works [Voronezh, Ona Lynv.), Such a circumstance was not investigated because of the nonlinear interaction of temperature and humidity with the help of analytical studies
Materials and Methods
We have equations for a plane isotropic material
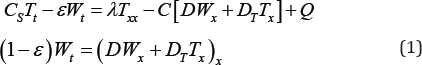
Coefficients Cs, ε, γ, C, D, DT- constant characterizing properties of materials when they are isotropic.
We will seek the stationary solution (1), provided that, the rate of change of temperature and humidity are constant in time t. This allows us to investigate (1) in the form:
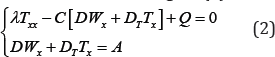
Then, from (2) where A - is a function dependent only on t,which is obtainined by integrating the second equation (2)
From (2) we have
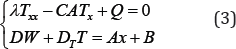
This problem is interesting in that the boundary conditions are mutually related, i.e.
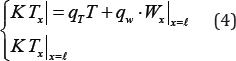
In this case, as the origin, the plane was chosen at x=0, and as the surface was chosen the plane located on the upper part of the material layer.
In (4), K - is the coefficient of thermal conductivity, qT , qw - coefficients that characterize the amounts of heat flux from the surface and its relationship to the moisture flux and the surface temperature of the drying material. Let the surface be heated with the power of irradiation of infrared waves, in the form
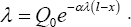
Where γ- the intensity ratio of the depth attenuation.
Consider the first equation (3), where the time enters the con parameter, so in this expression there are no time- produced, therefore, the integral with respect to x, the function in the interval variation of x, we can consider both a constant coefficient.
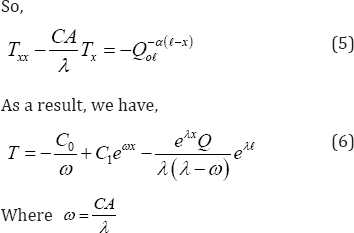
Now, to determine C0 and C1, which are constants of integration of the function (6), subordinate (agree) with the boundary conditions (4)
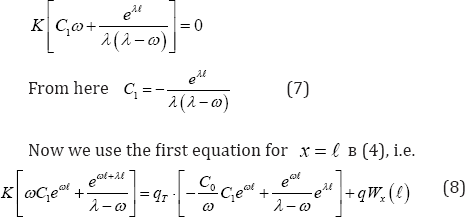
Here, there are connections for the flow of moisture
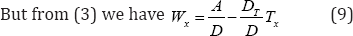
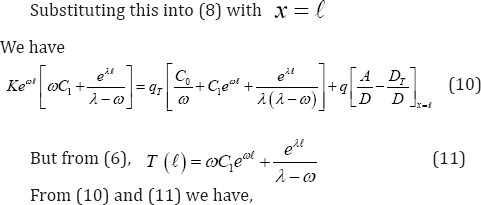
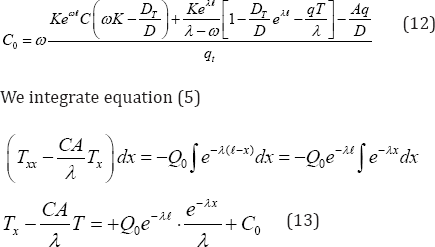
Where C0 - a certain integration constant
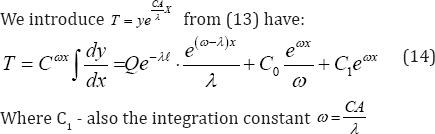
To determine the constants C1 and C2, we use the boundary conditions of the problem
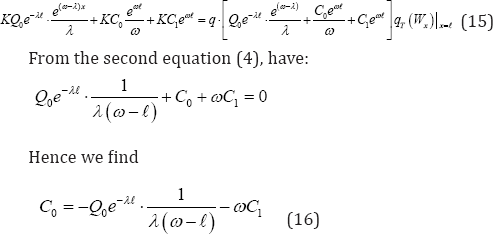
From (15) and (16), we find C1, but for this, still a manifestation of the attitude (15), where from the second equation with X = 𝓁, have:
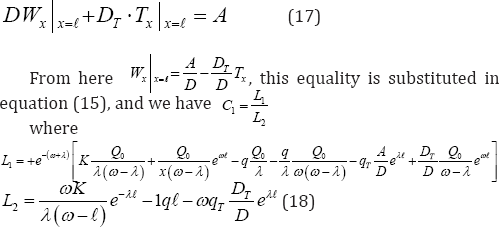
We have a concrete meaning C1 and C2
Now the function is uniquely determined by the solution[14].
From the second equation (2):
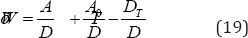
This determines the distribution of moisture during the drying process. The amount of moisture inside is determined by integrating over the layer:
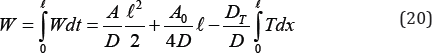
Where, T- an explicit function of x, from (14).
Conclusion
As can be seen from (20), increasing the layer thickness by moisture transfer affects more than the heat transfer process. Obtained explicit formulas also show (14, 20) this moisture distribution is more dependent on the thermal conductivity than the temperature distribution. The obtained results of the interaction of the temperature field and the humidity field against the background of the irradiation surface by infrared rays.
References
- Tikhonov AN, Samarskii AA Equations of mathematical physics.
- Kafarov VV, Glebov MB (1991) Mathematical modeling of the main processes of chemical production. High School p. 400.
- Safarov ZhE (2016) Model of moisture movement in capillary-porous materials. Tashkent State Technical University 1: 19-30.
- Safarov JE (2017) Research drying process with medical herbal gelio accumulation drying equipment. Journal of food processing & Technology 8(2): 1-2.






























