Proof of the Ethereal-Vortex Nature of Gravity
S Orlov*
Petrozavodsk State University, Russia
Submission: February 3, 2022; Published: February 15, 2022
*Corresponding author: S Orlov, Petrozavodsk State University, Russia
How to cite this article: S Orlov. Proof of the Ethereal-Vortex Nature of Gravity. Trends Tech Sci Res. 2022; 5(4): 555666. DOI: 10.19080/TTSR.2022.05.555666
Abstract
A proof is offered that gravity, celestial bodies and substances are created by cosmic, ethereal vortices.
Keywords:Vortex gravity; Cosmology; Cosmogony
Introduction
The founder of the theory of universal gravitation, I Newton [1], indicated material bodies as the source of forces of attraction. The forces of gravity, based on Newton’s calculations, are determined by the equation:
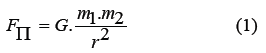
Where m1, m2 are the masses of bodies 1 and 2, respectively,
G=6.672 ∙10-11 N∙m2/kg2 – gravitational constant,
r is the distance between the bodies.
In 1915, 1916 A. Einstein proposed the general theory of relativity [2]. In this theory, gravitational effects are caused not by the force interaction of bodies and fields, but by the deformation of space-time itself. Deformation is associated with the presence of mass-energy. These theories have one common condition - the forces of attraction are created by the masses of bodies. Based on this condition, the conclusion follows - the forces of gravity act centrally - symmetrically. That is, they decrease with distance from the body equally, in all directions.
The above, classical model of gravity does not have any theoretical evidence and is based on observations and empirical calculations. Newton himself was not sure of this hypothesis and spoke out that the cause of attraction could be density changes in the cosmic gas - ether. It is known that Huygens called Newton’s hypothesis about the gravitational properties of bodies - absurd.
On the theory of Vortex Gravity
In the author’s theory of vortex gravity [3], it is proved that the forces of attraction are created by cosmic, ethereal vortices (torsion). The orbital speeds of rotation of the ether v(r) in the plane of each vortex decrease in inverse proportion to the square of the distance (r) from the center of rotation, in accordance with Kepler’s law.
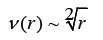
In accordance with Bernoulli’s principle, the pressure in this vortex increases in inverse proportion to the decrease in the speed of rotation of the ether. The cosmic vortex rotates in one plane. Therefore, the pressure changes the same in this plane. But the ethereal whirlwind also draws in its rotation the neighboring areas of the ether adjacent to it. In the theory of vortex gravity, it is proved that the speed of rotation of adjacent ethereal media v(r) decreases with the distance (s) from the central plane of rotation of the ether in inverse proportion to the cube of this distance rather than the square.
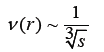
Accordingly, the pressure increases in inverse proportion to the cube of the distance from the central plane of the ether vortex. With such a change in pressure values in the ether, a cosmic, disk-shaped, low-dense field is created, into which all bodies are drawn. Therefore, all celestial systems - satellite, planetary, stellar (galaxies) and the Universe itself - are disk-shaped. This is a logical explanation of the ethereal plane-symmetric concept of the nature of gravity. The third chapter presents a complete, physical and mathematical proof of this gravitational model.
In the theory of vortex gravity [3], an equation was obtained to determine the forces of gravity at any cosmic point,
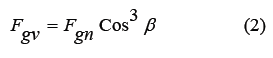
Cos3 β = Kg – gravity coefficient
Fgv - gravity force at an arbitrary point
Fgn - the gravitational force in the torsion plane (Equation 3)
β - the angle of deviation of the considered point from the central plane of the ether vortex.
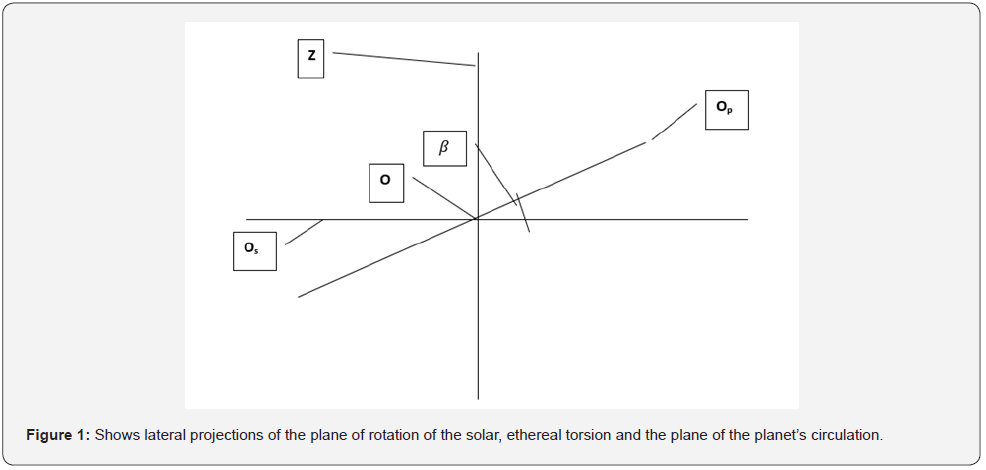
Note 1. The plane of the ether torsion in the solar system does not coincide with the plane of the ecliptic.
Note 2. Equation (2) is valid only at celestial points remote from the torsion center. In the center of the torsion, there are powerful, end, ethereal vortices, which reduce the pressure in the ether the same as in other central points of the torsion.
The gravitational force in the torsion plane acting on a body of mass m in the theory of vortex gravity is determined by the following equation:
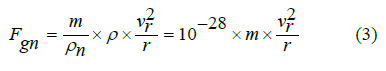
ρ= 8.85 x 10-12 kg/m3 - ether density [4]
ρn ~ 1017 kg/m3 is the density of nucleons that make up all bodies.
r - radius of considered ether vortex orbit
ve - speed of the ether in orbit r
m - body weight
Note 3. In the central plane of the ethereal torsion, Newton’s empirical equation (1) is equivalent to the vortex gravity equation (3).
Os - lateral projection of the orbit of the ethereal solar torsion
Op - lateral projection of the planet’s orbit
Z - axis of rotation of the torsion bar
O - projection of the line of intersection of the orbit of the planets with the gravitational orbit.
In the theory of vortex gravity, it is proved that the cosine of the angle of deviation of the plane of planetary circulation (angle β) from the plane of the ethereal, solar torsion is equal to the coefficient of orbit compression and is determined by the following relationship:
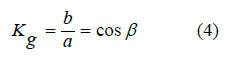
Kg - coefficient of compression of the orbit of a celestial body
a - the length of the semi-major axis of the planet’s orbit
b - the length of the minor semiaxis of the planet’s orbit
Since the lengths of the semi-axes of all planetary orbits are known, it is not difficult to determine the angle of deviation of the plane of any planetary orbit from the plane of the etheric, solar torsion in the solar system (Figure 1).
Physical and Mathematical Proof of the Vortex Gravity Equation
To assess the accuracy or reliability of the above equations 1 and 2, it is necessary to compare the results of the calculation according to these equations with the actual value. To do this, we use the law of mechanics - when a body moves along a curved trajectory, the centrifugal forces acting on this body at any orbital point are always equal to the centripetal forces. In our case, the centripetal forces are the forces of vortex gravity. Centrifugal forces are determined with high accuracy by a well-known equation.
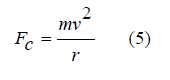
Let us determine and compare the value of solar gravitational (calculated - according to the classical law (1) and according to the theory of vortex gravity (2)) and centrifugal (actual) forces acting on two planets of the solar system at the vertices of the minor semiaxes of planetary orbits. At these vertices, the orbital, planetary planes have the maximum inclination from the plane of the etheric torsion (angle β). The coordinates of the planets are taken on the basis of [4].
Pluto
The semi-major axis of Pluto’s orbit a = 5906.375 x 106 km,
Semi-minor axis in = 5720.32 x106 km
Distance from the Sun to the top of the semi-minor axis of Pluto’s orbit d = 5907.963 x 106 km Orbital eccentricity e = 0.2488
Orbital compression coefficient Kpr = 1 - e2 = b/a = Cos β = 0.9685
Gravity coefficient Кg = b3/a3 = 0.9084
Radius of curvature at the top of the minor semiaxis Rb = a2/b = 6098.48 x 106 km
Pluto’s orbital velocity at perihelion Vp = 6.1 km/s
The same in aphelion Va = 3.71 km / s
The same top of the minor semiaxis Vb = 4.581km/s
The centrifugal forces at the top of the minor semiaxis, based on the above characteristics, are equal to:
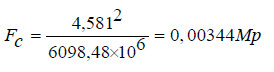
where Mp is the mass of Pluto
The force of solar gravity at the same point (according to Newton’s model - equation 1) is equal to:
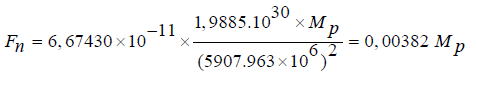
Difference with centrifugal forces + 11.1%)
Forces of vortex gravity, taking into account the gravitational coefficient or deflection (Equation 2).
Fgv = Fgn x Kg = 0,00382 x Mp x 0,9084 = 0,00347 Мp (discrepancy + 0.87%)
Mercury
a = 57.91 x 106, c = 56.67 x 106, d = 58.395 x 106
e = 0.2056, Kpr = b/a = Cos β = 0.9786,
Kg = b3/a3 = 0.9372.
Rb = 59.177 x 106,
Vp = 58.98 km/s,
Vd = 46.4775 km/s
Centrifugal forces Fc = 36.503 Mm
Gravitational forces:
According to Newton Fgn = 39.09 Mm, (difference +7.1%) According to the theory of vortex gravity Fgv = 39.09 × 0.9372 = 36.63 Mm (difference + 0.35%).
It is obvious that the calculation according to the theory of vortex gravity is an order of magnitude more accurate than the classical method and in its accuracy corresponds to the accuracy of astronomical measurements. With significant inclinations of the considered point, Newton’s formula becomes meaningless.
The calculation and comparison of centrifugal and gravitational forces at the centers of aphelion and perihelion of the orbits of Mercury and Pluto shows that at these points there is no discrepancy in the calculated values between centrifugal and vortex, gravitational forces (2). This circumstance corresponds to equation (2), since at these points the inclination to the central plane of the solar, gravitational torsion is zero. Consequently, the cosine of this inclination is equal to one, and then formula (2) is equivalent to formula (3) or Newton’s formula and centrifugal forces.
Conclusion
Based on the above calculations, it can be argued that the true cause of gravity is a decrease in pressure in the ether, which is caused by the vortex rotation of this ether. Accordingly, the gravitational-barial field, into which all substances are drawn, has the shape of a disk. Probably, Huygens was right about the assessment of Newton’s hypothesis about the gravitational properties of bodies, which created and creates many problems in the scientific world. The author outlined these problems in his article “Paradoxes of the Theory of Gravity” [5].
The theory of vortex gravity provides researchers with great scientific opportunities for new consideration of various physical properties and phenomena that have controversial explanations. Based on the theory of vortex gravity, the author proposed and published his physical models for the following phenomena:
a) origin and properties of Black Holes [6]
b) gravitational properties of atoms [7]
c) the genesis of the planet Earth [8]
d) equivalence of energy and atomic gravity [9]
e) invariance of the speed of light [10]
f) masses of celestial bodies [11]
g) photon mass [12]
h) reasons for the removal of the moon [13]
i) why did the global glaciation occur [14]
j) Causes of high and low tides [15]
the optimal trajectory of space flights [16].
References
- Newton I (1729) The Mathematical Principles of Natural Philosophy, 2.
- Albert E (1915) The field equations of gravitation. Reports of the meetings of the Prussian Academy of Sciences in Berlin pp. 844-847.
- Orlov S (2012) Foundation of vortex gravitation, cosmology and cosmogony. Global journal of science Frontier VA 12(1).
- Astronomical calendar. Moscow. Kosmosinform. Under the editorship of A.P. Gulyaeva.
- Orlov S (2014) Paradoxes of the Theory of Gravity. International Journal of Astrophysics and Space Science 2(1): 6-11.
- Orlov S (2017) Origin and Physical Properties of the Black Hole. International Journal of Astronautics and Aeronautical Engineering 2(1).
- Orlov S (2017) Gravitational Properties of Atom. Journal of Physics and Astronmy 5(3): 118.
- Orlov S (2017) Genesis of the planet Earth. Physics & Astronomy International Journal 1(1): 8-12.
- Orlov S (2018) Equivalence of energy and atomic gravitation. International Journal of Robotics and Automation p.1-3.
- Orlov S (2021) On Invariant Speed of Light. Natural Products Chemistry & Research 9(8): 414-416.
- Orlov AS (2019) Masses of Celestial Bodies. International Journal of Advanced Research in Physical Science (IJARPS) 6(2): 24-29.
- Orlov SA (2018) Photon Mass. Aerosp Eng Mech 2(1): 152-155.
- Orlov S (2015) Reasons for removal of the moon. Scientific Journal of Pure and Applied Sciences 4(9): 143-149.
- Orlov S (2021) Why Global Glaciations Happened. Journal of Physics Research & Reports p. 1-4.
- Orlov SA (2018) Gravitation - Flat Power Field. American Journal of Engineering Research and Reviews 1: 12.
- Orlov S (2016) On Optimal Trajectory in Space Flight. American Journal of Aerospace Engineering 3(2): 6-12.






























