Research Article

Analysis of Influence Factors on Annulus Pressure Changes when using Riserless Mud Recovery System for Deepwater Drilling Operations

Xin Li^1,2*, Jie Zhang^1,2*, Cuinan Li³, Chenghua Zhou⁴, Zhen Zhang⁴ and Ben Li⁵

¹State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, China

²Petroleum Engineering School, Southwest Petroleum University, China

³Engineering Technology Research Institute, CNPC Southwest Oil & Gasfield Company, China

⁴Drilling Engineering Research Institute, SINOPEC Southwest Petroleum Engineering Co., Ltd., China

⁵Research Institute of Petroleum Exploration and Development, CNPC Huabei Oilfield Company, China

Submission: September 24, 2021; Published: October 06, 2021

*Corresponding author: Xin Li and Jie Zhang, State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Petroleum Engineering School, Southwest Petroleum University, China

How to cite this article: Xin L, Jie Z, Cuinan L, Chenghua Z, Zhen Z, et al. Analysis of Influence Factors on Annulus Pressure Changes when using Riserless Mud Recovery System for Deepwater Drilling Operations. Trends Tech Sci Res. 2021; 5(2): 555660. DOI: 10.19080/TTSR.2021.05.555660

Abstract

The precise control of the annulus pressure involves drilling safety and cost, which has always been the focus of drilling engineering. In this paper, combined with the composition characteristics of the Riserless Mud Recovery (RMR) System, the calculation method of equivalent circulating density (ECD) and annulus pressure of the RMR system was proposed. According to the heat exchange characteristics of the RMR system, a mathematical model of the temperature field in the annulus was built. The variation of temperature field in the annulus of some well sections was simulated by computational fluid dynamics (CFD) software. Comparing the CFD analysis results with the calculation results of the mathematical model, the feasibility of the mathematical model was verified, and the temperature variation curve in the annulus was obtained. Based on the drilling data of a vertical well in the South China Sea, this paper analyzed the effects of seawater depth, cuttings concentration, and drilling pump displacement on the ECD and annulus pressure of the RMR system. The research results showed that the drilling fluid’s temperature in the RMR system’s annulus rises and then falls. Secondly, among the three factors of operating seawater depth, cuttings concentration, and drilling pump displacement, any factor will increase the ECD and annulus pressure of the RMR system.

Keywords:RMR system; Annulus pressure; ECD; Temperature field; Effect

Introduction

The limit seawater depth of riser used in offshore drilling engineering is 3,047m [1-3]. However, due to the impact force of seawater, the riser will vibrate at different frequencies, which makes it impossible for the riser to be used ideally in a deep-water environment [4-6]. Moreover, the manufacturing cost of the riser is prohibitive. Based on the above problems, and to effectively solve the impact of narrow safety pressure window, shallow gas, and shallow flow on offshore drilling engineering, the Norwegian AGR company invented the Riserless Mud Recovery (RMR) system [7-9]. As shown in Figure 1, the RMR system is mainly composed of three modules: Suction Module, Subsea Pump, and Return Line. The primary function of the suction module is to collect the drilling fluid returned from the annulus [10,11]. The primary function of the subsea pump is to adjust the pump speed so that the pressure exerted on the wellhead by the subsea pump is equal to the static pressure of the seawater at the depth, thereby achieving dual-gradient drilling (DGD) and achieving precise control of the annulus pressure [12,13]. Another function of the subsea pump is to provide power for the return of drilling fluid in the annulus. As the only channel for drilling fluid in the annulus to return to the platform, the selection and deployment of the return line will affect the lifting efficiency of drilling fluid. In a shallow water environment, the hose is usually used as a return line because the impact force of seawater in a shallow water environment is small, and hose winding on drill string will not occur, and using hose can reduce the manufacturing cost. However, in a deepwater environment, the hose is easily wound around the drill string due to the increased impact force of seawater. In order to ensure the safety of the drilling, it is necessary to use steel pipes as the mud return line in the deepwater environment.

In 2003, the RMR system was successfully commercialized for the first time in the Caspian Sea [14,15]. It is currently the most widely used and most successful DGD technology in the world. Compared with conventional offshore drilling, the RMR system has the following advantages:

a) The RMR system abandons the riser used in conventional offshore drilling, reducing drilling costs and requirements for drilling platforms and enabling the smaller drilling platforms to have the potential to drill in deep water.

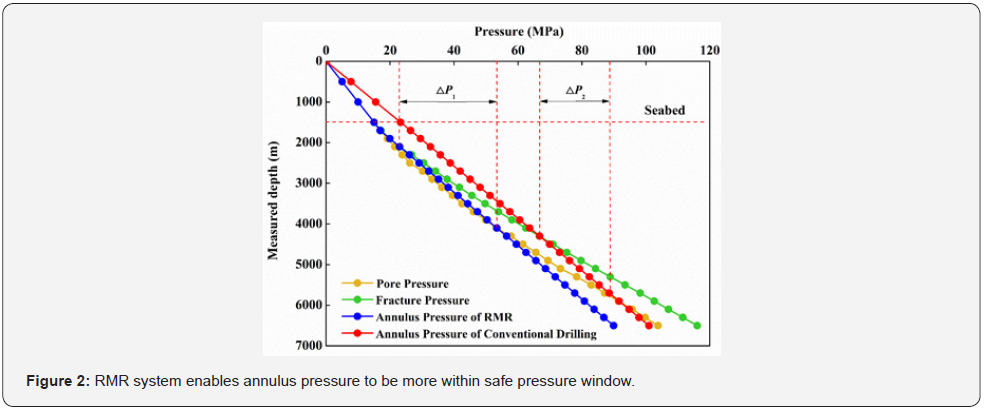
b) As shown in Figure 2, compared to conventional offshore drilling, the RMR system enables the annulus pressure to be more within the safe pressure window, thus enabling the number of casings to be reduced. The RMR system reduces the volume of mud used in the drilling process and reduces drilling costs.

c) The RMR system enables the cuttings at the bottom of the well to be lifted along the drilling fluid to the platform through the mud return line instead of being directly discharged to the seabed, thus meeting environmental requirements.

d) Because the RMR system uses a small diameter mud return line instead of a large diameter riser, the drilling fluid has a faster return flow rate.

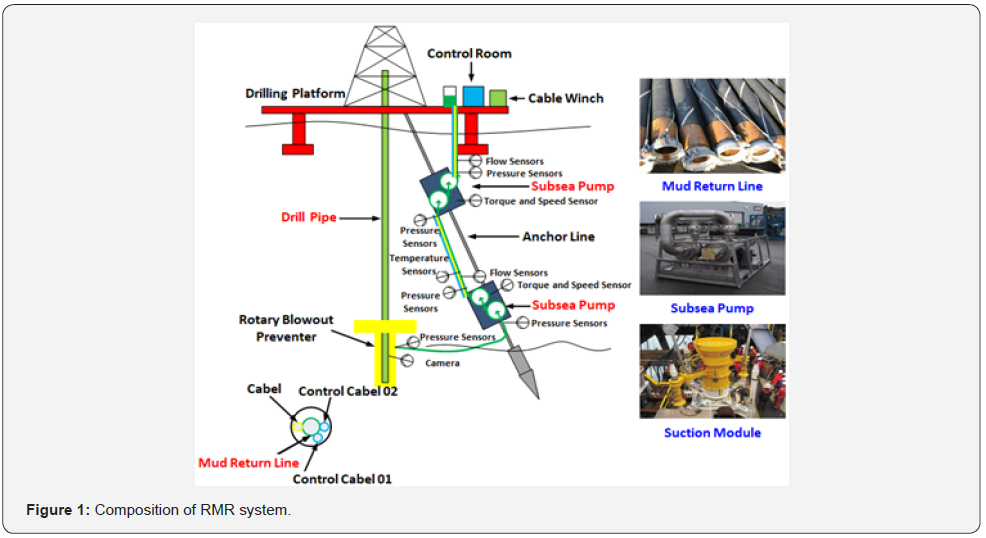
The RMR system has higher cuttings lifting efficiency than conventional offshore drilling. The RMR system is still not widely used in the deepwater field, the main reasons are:

a) The technical principle of the subsea pump is complex, and it is not currently possible to manufacture a subsea pump suitable for using in deepwater field.

b) There are some difficulties in detecting and handling the kick, and the well control operation is complicated.

c) Because the drill pipe is directly exposed to seawater, the drill pipe needs to have higher corrosion resistance and fatigue strength.

Well control has always been a significant concern of drilling engineering. Based on the drilling data of a vertical well in the South China Sea, this paper analyzed the factors affecting the annulus pressure of the RMR system by combining the dual-gradient pressure principle. The main influencing factors include seawater depth, cuttings concentration, and drilling pump displacement.

As the seasons and working place change, the operating seawater depth will change accordingly. According to the dual-gradient pressure principle of the RMR system, the subsea pump adjusts the pump speed so that the pressure acting on the wellhead is equal to the subsea static pressure at that depth. Therefore, when the operating seawater depth changes, the pressure exerted by the subsea pump on the wellhead will also change accordingly, thereby affecting the annulus pressure. This condition is the most significant difference compared to conventional offshore drilling when analyzing the annulus pressure of the RMR system. From the results of literature research, the influence of cuttings concentration on annulus pressure is often neglected, but the reasons for the neglect are not explained. The cuttings concentration is a function related to the rate of penetration. In this paper, the influence of different cuttings concentrations on the annulus pressure was obtained through calculation. The calculation results show whether the cuttings concentration can be neglected in the calculation of the annulus pressure. The flow rate of drilling fluid in the annulus varies with the drilling pump displacement change, resulting in different annulus pressure losses of drilling fluid in the annulus. Annulus pressure loss is an indispensable part of annulus pressure analysis. Based on the characteristics of the RMR system, the influence of different drilling pump displacement on annular pressure was analyzed in this paper.

Pressure field

The annulus pressure of the RMR system consists of three kinds of pressure:

a) The pressure exerted by the subsea pump on the wellhead, and it is also the inlet pressure of the subsea pump.

b) The circulating liquid column pressure is generated when the drilling fluid circulates in the annulus.

c) The pressure loss is caused by drilling fluid circulating in the annulus. The annulus pressure of the RMR system can be calculated via Equation 1:

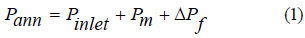
where P_ann is the annulus pressure, MPa; P_inlet is the inlet pressure of the subesea pump, MPa; P_m is the circulating liquid column pressure; ΔP_f is the annulus pressure loss, MPa.

The inlet pressure of the subesea pump can be calculated via Equation 2:

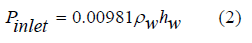
where ρ_w is the density of seawater, g/cm³; h_w is the seawater depth, m.

The circulating liquid column pressure can be calculated via

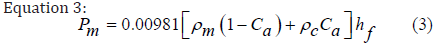
where ρ_m is the density of drilling fluid, g/cm³; ρ_c is the density of cuttings, g/cm³; C_a is the cuttings concentration, dimensionless; h_f is the formation depth, m.

When the fluid flow in the annulus is laminar, the annulus pressure loss can be calculated via Equation 4:

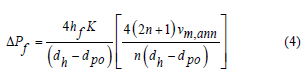
When the fluid flow in the annulus is turbulent, the annulus pressure loss can be written as in Equation 5:

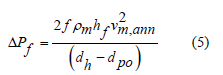
where K is the consistency coefficient of drilling fluid, Pa·sⁿ; n is the fluidity index of drilling fluid, dimensionless; v_m,ann is the flow rate of drilling fluid in the annulus, m/s; d_h is the diameter of wellbore, cm; d_po is the outer diameter of drill pipe, cm; f is the friction coefficient, dimensionless.

ECD can be calculated via Equation 6：

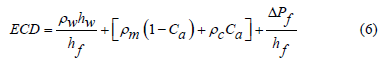
Equivalent static density (ESD) can be calculated via Equation 7:

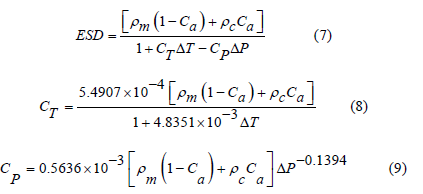
where C_T is the thermal expansion coefficient, dimensionless; C_P is the elastic compression coefficient, dimen-sionless; ΔT is the temperature difference between the drilling fluid at a certain depth and the platform, ^oC; ΔP is the pressure difference between the drilling fluid at a certain depth and the platform, MPa.

Cuttings concentration can be calculated via Equation 10:

where ROP is the rate of penetration, m/h; v_s is the setting velocity of cuttings in annulus, m/s; Q is the discharge capacity, L/s; A is conversion coefficient, dimensionless; d_s is the cutting diameter, cm.

Temperature field

Assumptions

A drilling fluid control volume of length dx was taken in the annulus, and the flow direction of drilling fluid was set to positive direction, and the following assumed conditions were made:

a) The temperature in any section of annulus perpendicular to the flow direction is uniform.

b) Ignore the heat conduction along the flow direction.

c) All physical properties are constants.

d) No heating measures are taken in the wellbore.

Mathematical model

The physical model of heat transfer process of annulus was shown in Figure 3.

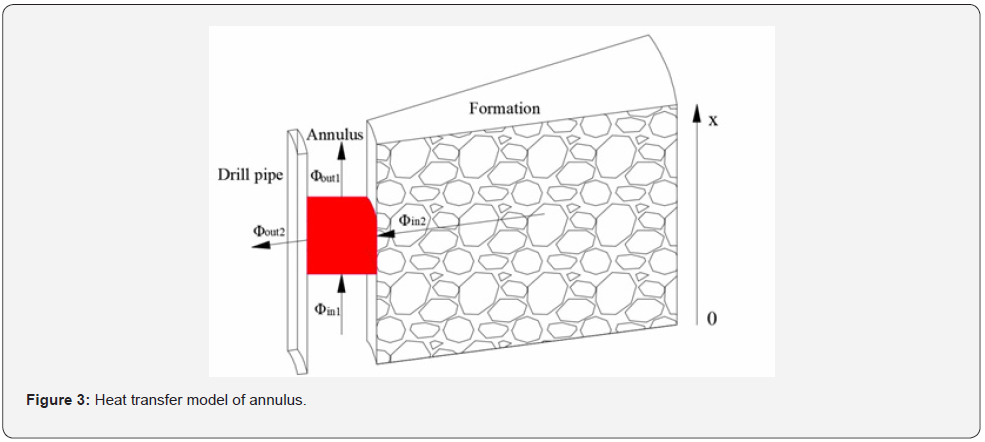
The heat injected from the lower surface of the control volume can be calculated via Equation 13:

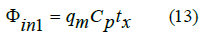
The heat transfer from the formation to the drilling fluid in the annulus can be calculated via Equation 14:

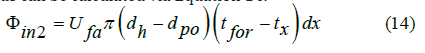
The temperature of the formation at depth x can be calculated via Equation 15:

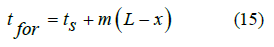
The heat that flows from the upper surface of the control volume can be calculated via Equation 16：

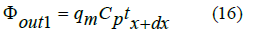
The heat transfer from the drilling fluid in annulus to the drilling fluid in drill pipe can be calculated via Equation 17:

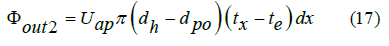
Combined with the boundary condition t_x=0=t_i, the calculation equation of the temperature of drilling fluid in annulus can be calculated via Equation 18:

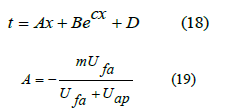
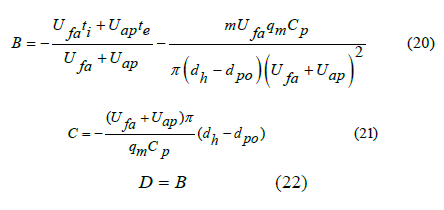
where U_fa is the heat transfer coefficient between the formation and the drilling fluid in annulus, W/(m²·^oC); U_ap is the heat transfer coefficient between the drilling fluid in annulus and the drilling fluid in drill pipe, W/(m²·^oC); t_i is the temperature of the drilling fluid at the bottom of well, ^oC; t_e is the temperature of the drilling fluid in drill pipe, ^oC; t_s is the surface temperature of formation, ^oC; m is geothermal gradient, ^oC/100m; q_m is the mass flow of drilling fluid through control volume, kg/s.

Numerical simulation

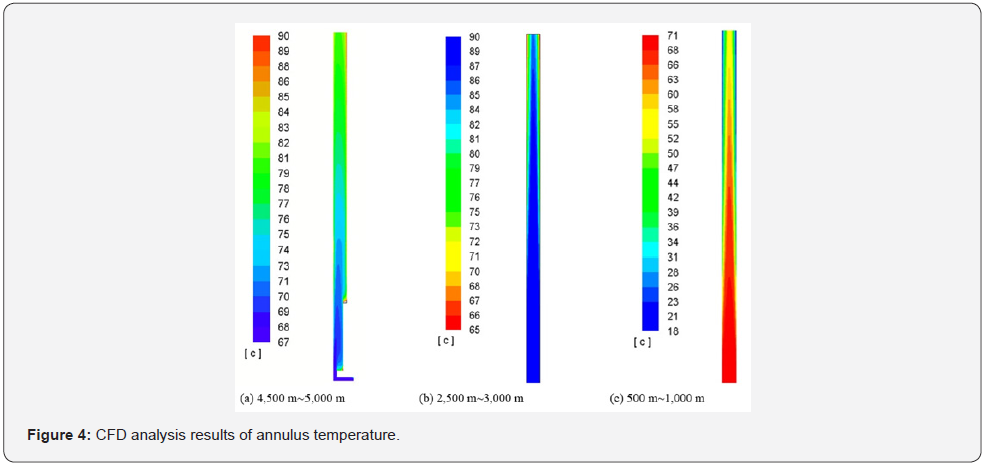
The temperature changes of the drilling fluid in the annulus at formation depth 500m-1,000m, 2,500m-3,000m, and 4,500m-5,000m were simulated. The basic parameters were shown in Table 1. The results from the analysis of the computational fluid dynamics (CFD) were shown in Figure 4. The temperature of the drilling fluid at the bottom of well was 67 ^oC. According to the result of CFD analysis, the temperature of drilling fluid at 4,500m was about 80 ^oC, 90 ^oC at 3,000m, 85 ^oC at 2,500m, 70 ^oC at 1,000m and 50 ^oC at 500m. From the results of the CFD analysis, the temperature of drilling fluid in the annulus first increased and then decreased.

Calculation results

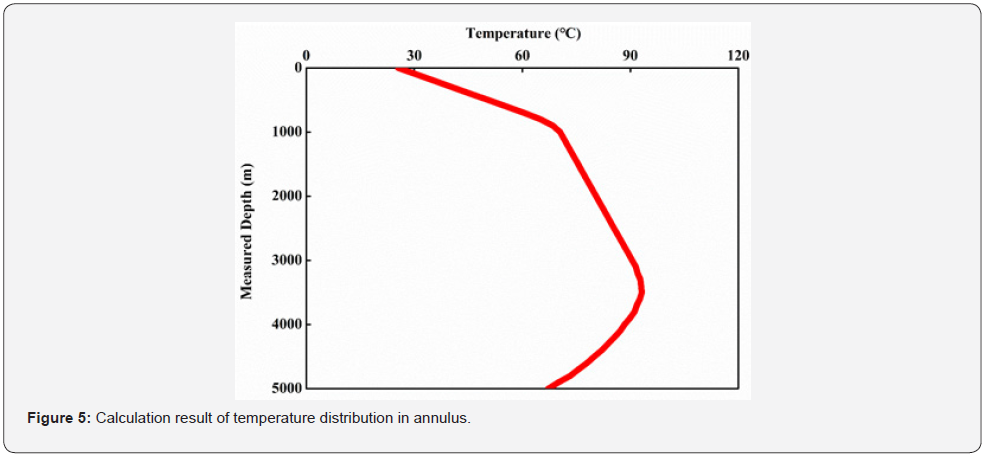
The temperature distribution of drilling fluid in the annulus was calculated by using the built mathematical model. The calculation results were shown in Figure 5.

f5

The calculation results were consistent with CFD analysis results, which show that the mathematical model built in this paper has sure accuracy. From the calculation results, there was a tendency for the temperature of the drilling fluid in the annulus to rise first and then decrease. This is because when the drilling fluid begins to return in the annulus, Φ_in2 > Φ_out2, the temperature of the drilling fluid will rise. As the drilling fluid continues to flow in the annulus, Φ_in2 < Φ_out2, the temperature of the drilling fluid will drop.

Results and Discussion

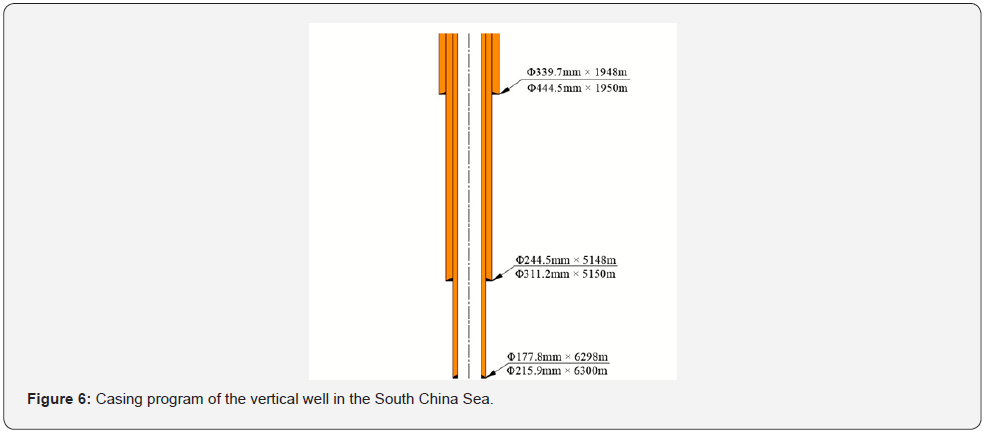
This paper’s calculations and analyses were based on drilling data from a vertical well in the South China Sea. Based on the drilling data of this well, the effects of operating seawater depth, cuttings concentration, and drilling pump displacement on ECD and annulus pressure were analyzed in this section. The critical parameters of the well were shown in Table 2. The casing program of the well was shown in Figure 6. The calculation of this section was based on the size of the intermediate casing.

Effect of operating seawater depth

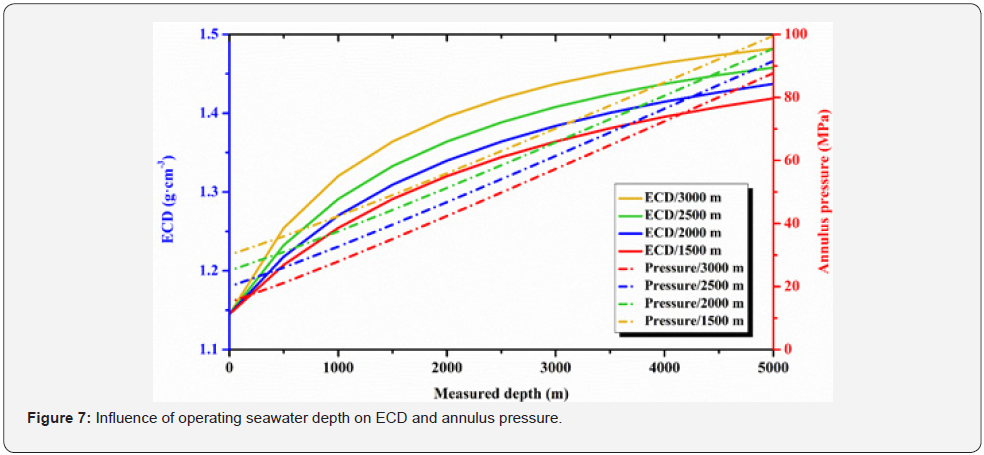
According to the dual-gradient pressure principle of the RMR system, the pressure exerted by the subsea pump on the wellhead is equal to the static pressure of the operating seawater depth. Therefore, the change in operating seawater depth mainly affects the pressure exerted by the subsea pump on the wellhead. By combining Equation 1 and Equation 6, the variation of ECD and annular pressure at operating seawater depths of 1,500m, 2,000m, 2,500m, and 3,000m was analyzed. The calculation results were shown in Figure 7.

As can be seen from Figure 7, as the operating seawater depth of the operating environment of the RMR system increased, the value of the ECD increased and the value of the annulus pressure increased. This is because, as the seawater depth increases, the pressure P_inlet acting on the wellhead increases, but the circulating liquid column pressure P_m and annulus pressure loss ΔP_f did not change. As a result, the ECD and annulus pressure increase. From the above analysis, the inlet pressure of the subsea pump P_inlet has an important influence on the change of the annulus pressure. Under the condition that the P_inlet is constant, certain measures should be taken to regulate the ECD so that the annulus pressure can pass through the safe pressure window to a greater extent.

Effect of cuttings concentration

By combining Equation 3 and Equation 6, the effects of different cuttings concentration on ECD and annulus pressure were explored. The cuttings content was set to 5%, 7%, 9% and 11% respectively. The calculation results were shown in Figure 8. As can be seen from Figure 8, as the cuttings concentration increased, the ECD and annulus pressure also increased. This is because, as the cuttings concentration increases, the circulating liquid column pressure P_m in-creases, but inlet pressure of subsea pump P_inlet and annulus pressure loss ΔP_f did not change. As a result, the ECD and annulus pressure increase.

Effect of drilling pump displacement

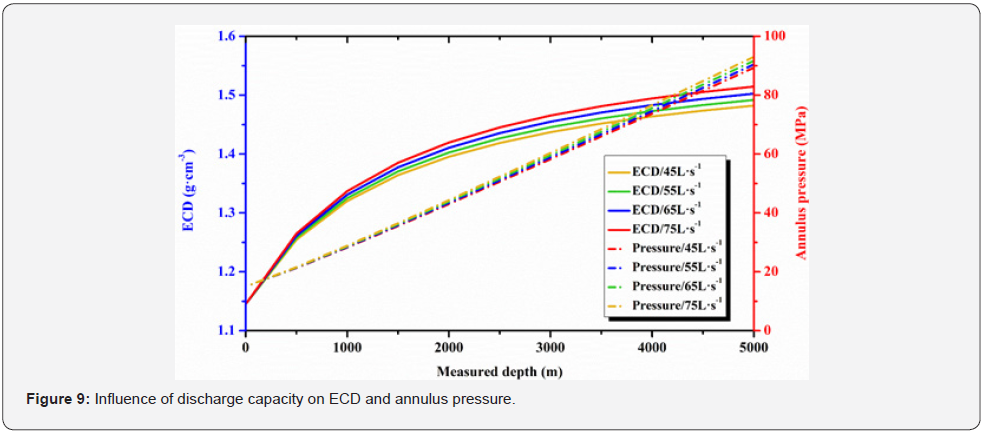
By combining Equation 4 and Equation 5, it can be known that the drilling pump displacement mainly affects the annulus pressure loss. The drilling pump displacement was set to 45 L/s, 55 L/s, 65 L/s, and 75 L/s, respectively. The effects of different drilling pump displacements on ECD and annulus pressure were explored. The calculation results were shown in Figure 9. It can be seen that as the discharge capacity increased, the ECD increased, and the annulus pressure increased slightly. The main reason is that as the discharge capacity increases, the flow velocity of the drilling fluid in the annulus becomes larger, and the pressure loss becomes larger. Combined with Equation 1 and Equation 6, it is obtained that the annulus pressure and the ECD is increased.

Conclusion

a) The temperature of the drilling fluid in the annulus was calculated using a mathematical model of the temperature field within the annulus. Through the calculation results, the temperature of the drilling fluid in the annulus of the RMR system increased first and then decreased.

b) As the operating seawater depth increases, the pressure Pinlet acting on the wellhead increased, but the circulating liquid column pressure Pm and annulus pressure loss ΔPf did not change. As a result, the ECD and annulus pressure increased.

c) As the cuttings concentration increased, the circulating liquid column pressure Pm increased, but inlet pressure of subsea pump Pinlet and annulus pressure loss ΔPf did not change. As a result, the ECD and annulus pressure increased.

d) As the drilling pump displacement increased, the flow velocity of the drilling fluid in the annulus became more extensive, and the pressure loss became larger, so the annulus pressure and ECD increased.

Acknowledgment

The authors thank the financial supports from the National Natural Science Foundation of China (No. 51274168), the National Key R&D Program of China (No. 2018YFC0310202), and the Southwest Petroleum University Graduate Research and Innovation Fund Key Program (No. 2020CXZD30).

References

1. Zhang J, Li X, Tang, X, Luo W (2019) Establishment and Analysis of Temperature Field of Riserless Mud Recovery System. Oil Gas Sci Technol 74(19): 1-9.
2. Li X, Zhang J, Tang X, Mao GZ, Wang PG (2020) Study on Wellbore Temperature of Riserless Mud Recovery System by CFD Approach and Numerical Calculation. Petroleum 6(2): 163-169.
3. Li X, Zhang J, Zhao HY, Zhang M, Sun XF, et al. (2020) Study on Lifting Efficiency of Cuttings in Return Line of Riserless Mud Recovery System. The 9^th International Conference on Informatics, Envi-ronment, Energy and Applications, p. 20-26.
4. Li X, Zhang J, Li CN, Li B, Zhao HY, et al. (2021) Variation characteristics of coal-rock mechanical properties under varying temperature conditions for Shanxi Linfen coalbed methane well in China. Journal of Petroleum Exploration and Production Technology 11(7): 2905-2915.
5. Li X, Zhang J, Wu CJ, Hong TY, Zheng YD, et al. (2021) Experimental Research on the Effect of Ultrasonic Waves on the Adsorption, Desorption, and Seepage Characteristics of Shale Gas. ACS Omega 6(26): 17002-17018.
6. Li X, Zhang J, Li RX, Qi Q, Zheng YD, et al. (2021) Numerical Simulation Research on Improvement Effect of Ultrasonic Waves on Seepage Characteris-tics of Coalbed Methane Reservoir. Energies 14(15): 4605.
7. Li X, Zhang J, Zheng YD, Li CN, Li ZL, et al. (2021) Experimental Research and Numerical Analysis of the Attenuation Law of Ultrasound Propagating in Shale. Journal of Physics Conference Series 1980(1): 34-40.
8. Li X, Zhang J, Li CN, Chen WL, He JB, et al. (2021) Characteristic Law of Borehole Deformation Induced by the Temperature Change in the Surrounding Rock of Deep Coalbed Methane Well. Journal of Energy Resources Technology 144(6): 063003.
9. Zhang J, Zhao ZP, Li X, Zheng YD, Li CN, et al. (2021) Research on the mechanism of the influence of flooding on the killing of empty wells. Journal of Petroleum Exploration and Production Technology 11(9): 3751-3598.
10. Godhavn J (2010) Control requirements for automatic managed pressure drilling system. SPE Drill Complet 25(3): 336-345.
11. Marcellinus A, Ojinnaka S, Joseph JB (2018) Full-course drilling model for well monitoring and stochastic estimation of kick. Journal of Petroleum Science and Engineering 166(4): 33-43.
12. Rezk R (2013) Safe and Clean Marine Drilling with Implementation of “Riserless Mud Recovery Technolo-gy-RMR”. SPE Arctic and Extreme Environments Conference.
13. Stave R, Nordas P, Fossli B (2014) Safe and Efficient Tophole Drilling using Riserless Mud Recovery and Managed Pressure Cementing. Offshore Technology Conference.
14. Zhang J, Zou JW, Nie K, Shao YS, Zhao YC, et al. (2017) Numerical Simulation of Wellhead Back Pressure in Underbalanced Drilling. Energy Procedia 107: 150-156.
15. Zhang J, Li CN, Zeng FH, Chen P, Zhang Z, et al. (2012) To Start up Extra-heavy Oil or Bitumen Wells by Solvents after Drilling. SPE Heavy Oil Conference Canada held in Calgary, Alberta, Canada.