Research Article

Line-by-Line Sweeping Method in Hydraulic Head Distribution

Farhad Sakhaee*

School of Engineering, Saint Louis University, USA

Submission: August 17, 2021; Published: August 31, 2021

*Corresponding author: Farhad Sakhaee, School of Engineering, Saint Louis University, USA

How to cite this article: Farhad Sakhaee. Line-by-Line Sweeping Method in Hydraulic Head Distribution. Trends Tech Sci Res. 2021; 5(2): 555656. DOI: 10.19080/TTSR.2021.05.555656

Abstract

Numerical solutions have been extensively used in recent decades to solve engineering problems in different fields such as fluid dynamics, heat transfer and soil mechanics. In this study a hybrid implicit finite difference approach has been used to calculate the hydraulic water head distribution which is a combination of Gauss-Seidel and Alternating Direction Implicit method. By solving seepage equation for stable flow condition in a two-dimensional homogenous and isotropic environment, water head distribution from high to low values is calculated from four neighboring cells. Results showed by travelling from right to left in head contours, density and value increased. Water head has been divided into 12 equipotential lines. The benefit of using such numerical solutions is their high accuracy and consistency.

Keywords: Numerical Simulation; Finite difference method; Line sweeping; Hydraulic head distribution

Introduction

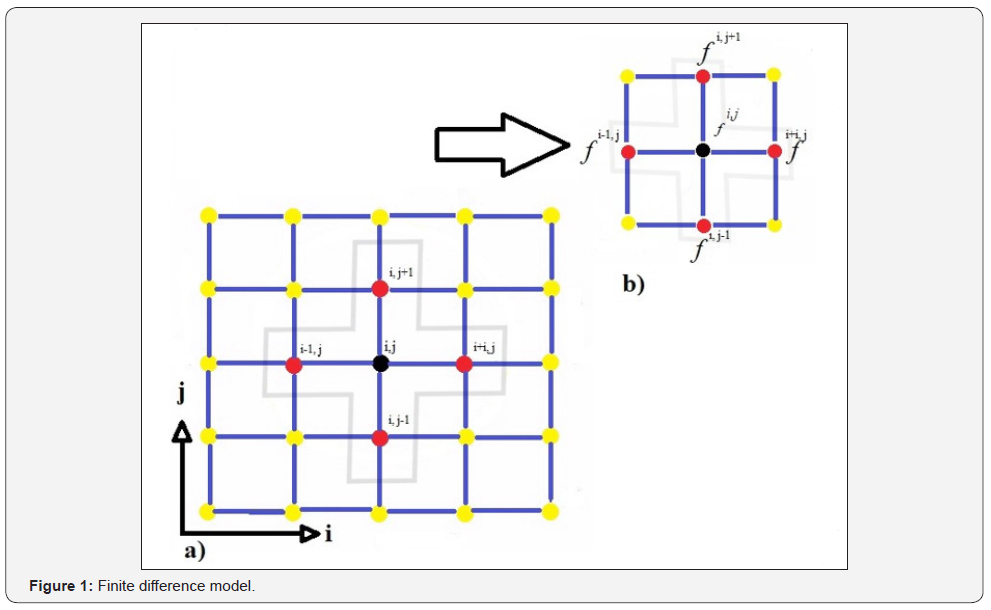
An engineering problem with too many assumptions and simple mathematical model results in analytical solution which is a good approximation to reality [1-3]. On the other hand, engineering problem with low assumptions and more complex math models ends in numerical solutions [4-7]. Numerical models are classified into three major categories. Finite difference, finite volume, and finite element modeling. Finite difference has been developed by Euler in 1768. The earliest mathematical paper describing the technique date back to Shellback’s work of 1851 [8]. One other method is finite volume method which is almost the same with finite difference method except an integration step ahead of finite difference [9-11]. From 1950 finite element method (FEM) has been developed and extensively used specifically for structural frame analysis etc. [12-14]. Any finite difference model includes two main parts. First is domain discretization which is shown in Figure 1 below. And the second component is equation discretization. Equation (1) shows a sample of equation used in finite difference method.

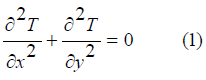
In discretization of equation an approximation based on teylor’s expansion has been used [15-17]. Beside, elements relation in the modeling domain has a high degree of importance. Finite difference can be used in advection-diffusion equation, conservation of mass or in solving Navier-Stokes equations both in explicit and implicit formats [18-20]. Other advantages of using numerical solutions is their consistency, stability, convergency and finally their accuracy. Courant number is responsible for stability of the model [21].

Method

Alternating direction implicit (ADI)

In this method equations are solved in a sequential order in terms of rows and columns of a matrix respectively. The whole idea is to solve the first set of equations, rows per say in first time step and the others (columns) in next time step [22,23].

Gauss-seidel method

It is an iterative method used to solve a system of linear equations which is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel [8]. In this iterative method equation with higher coefficient used as a base for starting equation.

Line by line sweeping method

This method is a combination of Gauss-Seidel and ADI method. By solving seepage equation for stable flow condition in a two-dimensional seepage environment we have equation (2) as below. Considering homogenous environment (K is constant in all directions) and isotropic condition (K_x = K_y) equation (2) simplified into equation (3).

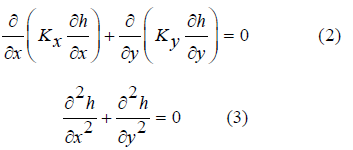
By applying second order finite difference method, equation (3) results in equation (4).

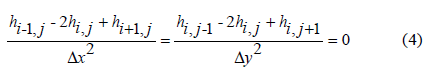
If ∆x = ∆y, then hi, j is calculated from four neighborhood cells as presented in Figure 1 as well as equation (5) below.

Boundary and initial conditions

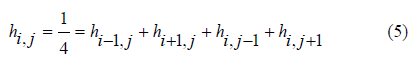
Figure 2 shows a schematic of problem. This study investigates hydraulic head distribution based on a line-by-line implicit sweeping method. A 4×6 matrix has been considered in which boundary conditions at the left and right sides as well as up and down of the domain was given as known values in blue circles in terms of meters of water head. In this study water head stands at 5 meters at the left-hand side and eventually reaches to zero at the right-hand side. Boundary conditions and their values are shown in blue circles. Calculated values are presented in central red circles having initial values of two meters of water starting from lower case e and end at lower case d.

By applying the sweeping method from second row, all red circles have been calculated from four neighboring method which has been mentioned earlier. In next step by starting from second column and having previously calculated results as initial known values for this step, values of second iteration were calculated. To check the model convergence, a convergence condition has been applied.

Successive Over Relaxation (SOR)

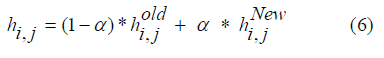
α = 1.5 considered as relaxation coefficient and should be higher than one.

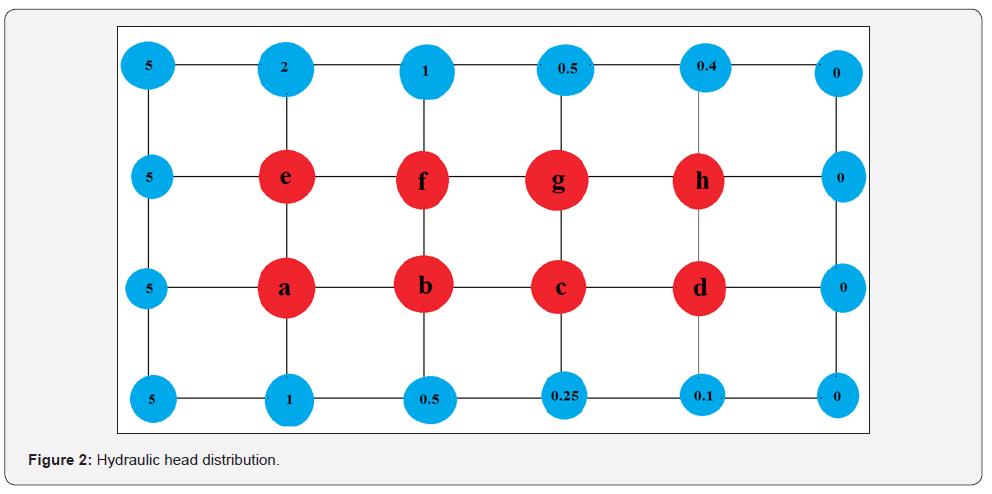
Results

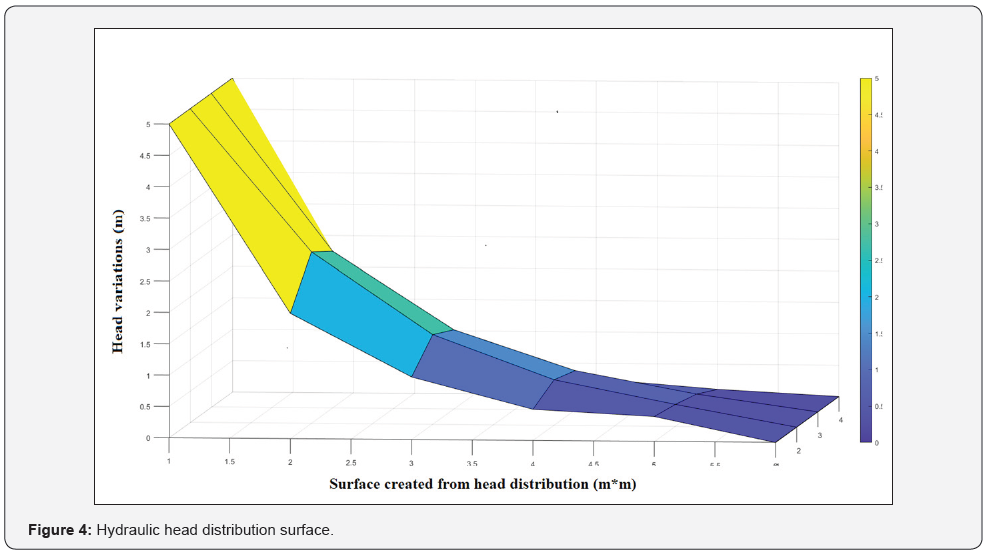
Figure 3 shows distributed head contours from high to low values. By travelling from right to left contours density and value increased. In fact, the height of five meters of water has been divided into 12 equipotential lines, in which each single line stands for a cross-sectional head at that height of water. The reason of having low congestion of equipotential lines at the right-hand side (lower head values) of Figure 3 is the mild slope of head distribution as it is presented in Figure 4, hence equipotential lines are in further distances in comparison to the left -hand side (Higher head values). Figure 4 below shows a schematic of head distribution surface.

Conclusion

In this study, with the help of a numerical approach a fluid dynamic solution has been developed for a hydraulic head distribution of water throughout a hybrid line-by-line procedure which is a derivation of Alternating Direction Implicit Method (ADI) and Gauss-Seidel method. Numerical solutions have high accuracy and consistency as well as convergency and stability. These characteristics gives us a privilege in replacing them with many analytical and traditional fluid dynamic solutions. Their accuracy leads in having less errors in our results, and their convergency ends in reaching the almost same algebraic solution results.

References

1. Cai R, Zhang N (2003) Explicit analytical solutions of 2-D laminar natural convection. International journal of heat and mass transfer 46(5): 931-934.
2. Crowdy DG (2006) Analytical solutions for uniform potential flow past multiple cylinders. European Journal of Mechanics-B/Fluids 25(4): 459-470.
3. Khater MM, Bekir A, Lu D, Attia RAM (2021) Analytical and semi‐analytical solutions for time‐fractional Cahn-Allen equation. Mathematical Methods in the Applied Sciences 44(3): 2682-2691.
4. Anderson JD, Wendt J (1995) Computational fluid dynamics. Springer, pp. 206.
5. Griebel M, Dornseifer T, Neunhoeffer T (1998) Numerical simulation in fluid dynamics: a practical introduction. SIAM.
6. Date AW (2005) Introduction to computational fluid dynamics. Cambridge University Press.
7. Holt M (2012) Numerical methods in fluid dynamics. Springer Science & Business Media.
8. Curnier A (1994) Computational methods in solid mechanics. Springer Science & Business Media, p. 29.
9. Moukalled F, Mangani L, Darwish M (2016) The finite volume method in computational fluid dynamics. Springer, pp. 113.
10. Peric M (1985) A finite volume method for the prediction of three-dimensional fluid flow in complex ducts.
11. Barth T, Ohlberger M (2004) Finite volume methods: foundation and analysis. Encyclopedia of computational mechanics. 1(15): 1-57.
12. Zienkiewicz OC (1977) The finite element method. McGraw-hill London, p. 3.
13. Reddy JN (2019) Introduction to the finite element method. McGraw-Hill Education.
14. Bathe KJ (2007) Finite element method. Wiley encyclopedia of computer science and engineering, p. 1-12.
15. Zhou S (2002) Formally exact'first-order Taylor series expansion for density functional theory. New Journal of Physics 4(1): 36-38.
16. Li Q, Qiu Z, Zhang X (2017) Eigenvalue analysis of structures with interval parameters using the second-order Taylor series expansion and the DCA for QB. Applied Mathematical Modelling 49: 680-690.
17. Franceschini S, Tsai C, Marani M (2012) Point estimate methods based on Taylor Series Expansion–The perturbance moments method–A more coherent derivation of the second order statistical moment. Applied Mathematical Modelling 36(11): 5445-5454.
18. Dehghan M (2004) Numerical solution of the three-dimensional advection–diffusion equation. Applied Mathematics and Computation 150(1): 5-19.
19. Menaldi JL, Sritharan SS (2002) Stochastic 2-D Navier - Stokes Equation. Applied Mathematics & Optimization 46(1).
20. Sakhaee F, Khalili F (2021) Sediment pattern & rate of bathymetric changes due to construction of breakwater extension at Nowshahr port. Journal of Ocean Engineering and Science 6(1): 70-84.
21. Shchepetkin AF (2015) An adaptive, Courant-number-dependent implicit scheme for vertical advection in oceanic modeling. Ocean Modelling 91: 38-69.
22. Tysinger T, Caughey D (1992) Alternating direction implicit methods for the Navier-Stokes equations. AIAA journal 30(8): 2158-2161.
23. Marchuk GI (1990) Splitting and alternating direction methods. Handbook of numerical analysis 1: 197-462.