Global Neighbourhood Algorithm for Reduction of Actual Power Loss
Kanagasabai Lenin*
Department of EEE, Prasad V Potluri Siddhartha institute of technology, India
Submission: September 26, 2020;Published: November 19, 2020
*Corresponding author: Kanagasabai Lenin, Department of EEE, Prasad V Potluri Siddhartha institute of technology, India
How to cite this article: Kanagasabai L. Global Neighbourhood Algorithm for Reduction of Actual Power Loss. Trends Tech Sci Res. 2020; 4(4): 555642 10.19080/TTSR.2020.04.555642
Abstract
In this paper, Global Neighbourhood Algorithm (GNA) is utilized for solving the optimal reactive power problem. Projected algorithm is mainly maintaining the balance between global and local exploration. Most outstanding incorporation (g1) is used as a premium measure for the local optimal solution and act as first and foremost set of the supreme recognized solution. In subsequent iteration, 50% of the (m) created solutions will be engendered close to the most outstanding solution of the neighbourhood by using a suitable shift operator. Then the other 50% of the (m) engendered solutions is formed from the entire explore space, and reason for that is to authorize the exploration in search space, since solutions close to the most outstanding solution is chosen then local solution in the region can be found .Proposed Global Neighbourhood Algorithm (GNA) has been tested in standard IEEE 14,300 bus test system and simulation results show the proposed algorithm reduced the real power loss considerably
Keywords: Optimal Reactive Power; Transmission loss; Global Neighbourhood Algorithm
Introduction
Reactive power problem plays a key role in secure and economic operations of power system. Optimal reactive power problem has been solved by a various type of methods [1-6]. Nevertheless, numerous scientific difficulties are found while solving problem due to an assortment of constraints. Evolutionary techniques [7-15] are applied to solve the reactive power problem [16-19], but the key problem is some algorithms stuck in local optimal solution & failed to balance the Exploration & Exploitation during the search of global solution. In this paper Global Neighbourhood Algorithm (GNA) is utilized for solving the optimal reactive power problem. Projected algorithm is mainly maintaining the balance between global and local exploration. A set of arbitrary solutions are initially engendered from the global exploration space, and then the most excellent solution will give the optimal value. In each iteration there are two sets of engendered solutions; one from the global exploration space and the other set of solutions will be engendered from the neighbourhood of the most excellent solution. Every iteration 25 feasible solutions were engendered from the entire exploration space and the other 25 solutions were engendered from the neighbourhood of the fittest solution. Proposed Global Neighbourhood Algorithm (GNA) has been tested in standard IEEE 14,300 bus test system and simulation results show the proposed algorithm reduced the real power loss considerably.
Problem Formulation
Objective of the problem is to reduce the true power loss:

Global Neighbourhood Algorithm
Global Neighbourhood Algorithm finds the optimized value amongst the local optimal values by exchanging the exploration and exploitation suitably. Entire search space has been searched by the exploration. In the neighbourhood the search is done by the Exploitation from the most excellent solution of formed solutions. The main function assumed in the proposed methodology

Where, y1, y2 ,…, yn are the dissimilar amalgamation of the solution progression.
Optimal combination has to be identified (y1, y2 ,…, yn) that gives the optimized value for the objective function. In common each of the variables (y1, y2 ,…, yn) can be selected in(n1, n2 ,…, nn) methods correspondingly, then the probable solutions this will acquiesce(n_1,n,..,n_n ) solutions. In the proposed Global Neighbourhood Algorithm set of (m) arbitrary solutions are engendered from the set of all probable solution, where ,( y1, y2 ,…, yn) can be selected in(n1, n2 ,…, nn) methods. Engendered solutions will emerge as
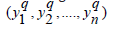
where q=1, 2,..,m.
For the solutions fitness value will be calculated and classified as
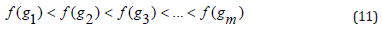
g1 = (y’1, y’2 ,…, y’n) is the solution progression with most excellent fitness.
The objective distance is calculated by
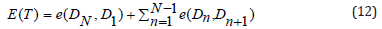
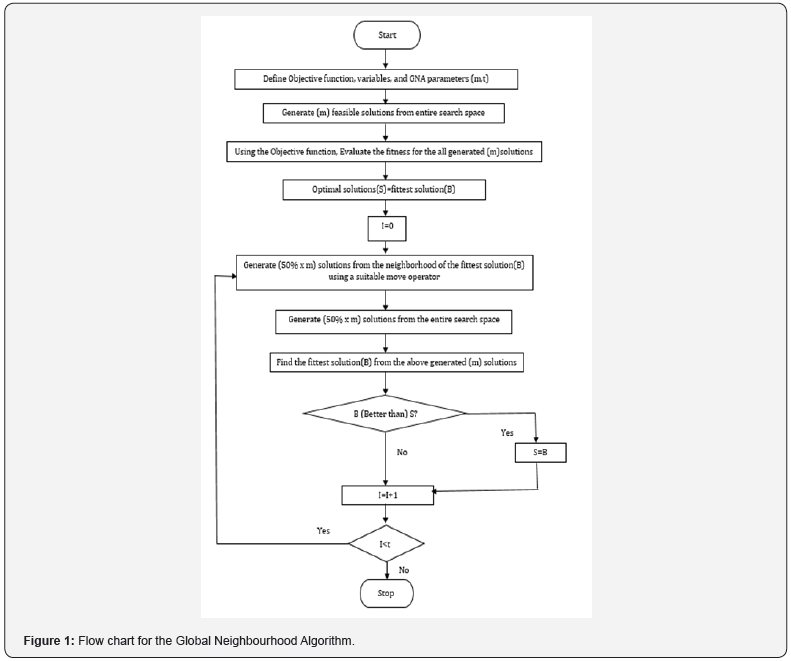
Most outstanding incorporation (g1) is used as a premium measure for the local optimal solution and act as first and foremost set of the supreme recognized solution. In subsequent iteration, 50% of the (m) created solutions will be engendered close to the most outstanding solution of the neighbourhood by using a suitable shift operator. Then the other 50% of the (m) engendered solutions is formed from the entire explore space, and reason for that is to authorize the exploration in search space, since solutions close to the most outstanding solution is chosen then local solution in the region can be found . Function has to be optimized and the capacity having additional local optima, which will power to get stuck at one of those local optima. Subsequently, the most excellent solution from the above (m) solutions (50%, 50%) is calculated. new value for the most excellent solution is weighed against to most excellent recognized solution and when it finds superior it will be swapped. This procedure is repetitive until a definite end criterion is met. Stop criterion is pre-specified number of iterations. Figure 1 shows the flow chart of the Global Neighbourhood Algorithm [20,21].
a) commence
b) describe the objective function, variables, parameters
c) From the complete explore space engender (m) feasible solutions.
d) Fitness value for all produced (m) solutions is computed by the objective function
e) Best Optimal solution (S) = fittest solution (B)
f) I=0
g) By using a suitable move operator create (50%×m) solutions from the neighbourhood of the fittest solution (most outstanding)
h) From the complete search space engender (50%×m) solutions.
i) Locate the best fittest solution (most outstanding) from above formed (m) solutions.
j) Is most outstanding solutions (superior than) optimal solution (S)?
k) If yes, then S = B
l) If no, I=I+1
m) Is I< t?
n) If yes, then go to step g Or else stop.
Depict objective function
Initialize the values for all parameters (m)
From the exploration space engender (m) feasible solutions
From the objective function calculate the fitness value
Best Optimal solution= the most outstanding solution.
i=1
Do while I < t,++
From the neighbourhood of the most outstanding solution engender 50% × m solutions
From the explore space engender 50% × m solutions
From the (m) created solution find out the most outstanding solution
If most outstanding solution is less (superior) than optimal solution; Best Optimal solution=most outstanding solution
End If
End DO
Simulation Results
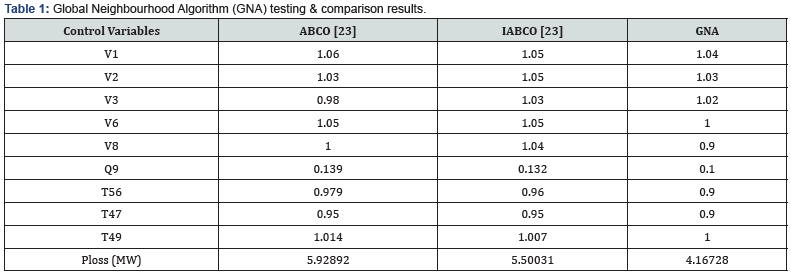
At first in standard IEEE 14 bus system the validity of the proposed Global Neighbourhood Algorithm (GNA) has been tested & comparison results are presented in Table 1. Then IEEE 300 bus system [22] is used as test system to validate the performance of the Global Neighbourhood Algorithm (GNA). Table 2 shows the comparison of real power loss obtained after optimization [23- 25].

Conclusion
In this work, Global Neighbourhood Algorithm (GNA) is successfully solved the optimal reactive power problem. GNA finds the optimized value amongst the local optimal values by exchanging the exploration and exploitation suitably. Entire search space has been searched by the exploration. In the neighbourhood the search is done by the Exploitation from the most excellent solution of formed solutions. Proposed Global Neighbourhood Algorithm (GNA) has been tested in standard IEEE 14,300 bus test system and simulation results show the proposed algorithm reduced the real power loss considerably.
References
- Lee KY, ParkYM, OrtizJL(1984) Fuel-cost minimisation for both real and reactive-power dispatches. Proceedings Generation. Transmission and Distribution Conference 131(3): 85-93.
- Deeb NI, ShahidehpourSM (1998) An efficient technique for reactive power dispatch using a revised linear programming approach. Electric Power System Research 15(2): 121-134.
- Bjelogrlic MR, Calovic MS, Babic BS (1990) Application of Newton’s optimal power flow in voltage/reactive power control. IEEE Trans Power System 5(4): 1447-1454.
- Granville S (1994) Optimal reactive dispatch through interior point methods. IEEE Transactions on Power System9(1): 136-146.
- Grudinin N (1998) Reactive power optimization using successive quadratic programming method. IEEE Transactions on Power System 13(4): 1219-1225.
- Wei Y, Yu J, Yu DC, Bhattarai K (2006) A new optimal reactive power flow model in rectangular form and its solution by predictor corrector primal dual interior point method. IEEE Trans Pwr 21(1): 61-67.
- Aparajita M, Vivekananda M (2015) Solution of optimal reactive power dispatch by chaotic krill herd algorithm. IET GenerTransmDistrib 9(15): 2351-2362.
- Hu Z, Wang X, Taylor (2010) Stochastic optimal reactive power dispatch: Formulation and solution method. Electr. Power Energy Syst 32(6): 615-621.
- Mahaletchumi AM, Nor RHA, MohdHerwan S,Mahfuzah M, Rosdiyana S(2016)Multi-Objective Evolutionary Programming (MOEP) Using Mutation Based on Adaptive Mutation Operator (AMO) Applied for Optimal Reactive Power Dispatch. ARPN Journal of Engineering and Applied Sciences11(14).
- Pandiarajan K, Babulal CK (2016) Fuzzy harmony search algorithm based optimal power flow for power system security enhancement. International Journal Electric Power Energy Syst 78: 72-79.
- Mahaletchumi M, Nor Rul HA, MohdHerwan S, Mahfuzah M, Rosdiyana S(2016)Benchmark Studies on Optimal Reactive Power Dispatch (ORPD) Based Multi-objective Evolutionary Programming (MOEP) Using Mutation Based on Adaptive Mutation Adapter (AMO) and Polynomial Mutation Operator (PMO). Journal of Electrical Systems12(1).
- Rebecca Ng SM, MohdHerwan S, Zuriani M (2016)Ant Lion Optimizer for Optimal Reactive Power Dispatch Solution. Journal of Electrical SystemsSpecial Issue AMPE2015 pp. 68-74.
- Gagliano A, Nocera F(2017)Analysis of the performances of electric energy storage in residential applications. International Journal of Heat and Technology 35(1): S41-S48.
- Caldera M, Ungaro P, Cammarata G, Puglisi G (2018) Survey-based analysis of the electrical energy demand in Italian households. Mathematical Modelling of Engineering Problems5(3): 217-224.
- MBasu (2016) Quasi-oppositional differential evolution for optimal reactive power dispatch. Electrical Power and Energy Systems78: 29-40.
- Saddique, Muhammad S, Abdul RBh, Shaikh SH, Muhammad KS, et al. (2020) Solution to optimal reactive power dispatch in transmission system using meta-heuristic techniques-Status and technological review. Electric Power Systems Research 178: 106031.
- Sattar, Muhammad K, Aftab A, Saqib F, Syed SUH, et al. (2020)Ramp rate handling strategies in dynamic economic load dispatch (DELD) problem using grey wolf optimizer (GWO). Journal of the Chinese Institute of Engineers 43(2): 200-213.
- Li J, Ni W, Dao Z, Weihao H, Qi H, et al. (2020) Optimal reactive power dispatch of permanent magnet synchronous generator-based wind farm considering levelised production cost minimisation. Renewable Energy 145: 1-12.
- Ettappan M, Vimala V, Ramesh S, Thiruppathy KV (2020) Optimal Reactive Power Dispatch for Real Power Loss Minimization and Voltage Stability Enhancement using Artificial Bee Colony Algorithm. Microprocessors and Microsystems 76: 103085.
- WeiseT (2009) Global Optimization Algorithms - Theory and Application. Germany.
- Azmi A, Harold W, Lewis III (2013) A New Optimization Algorithm for Combinatorial Problems. International Journal of Advanced Research in Artificial Intelligence2(5).
- IEEE(1993)The IEEE-test systems.
- Chandragupta MKS, Subramanian R, Purrnimaa SSR (2017) Reactive power optimization in a power system network through metaheuristic algorithms. Turkish Journal of Electrical Engineering & Computer Science25: 4615-4623.
- Reddy SS (2017) Optimal Reactive Power Scheduling Using Cuckoo Search Algorithm. International Journal of Electrical and Computer Engineering 7(5): 2349-2356.
- Reddy SS, BijwePR, AbhyankarAR (2014) Faster evolutionary algorithm based optimal power flow using incremental variables. Electrical Power and Energy Systems54: 198-210.






























