Review Article

Integration of Operability Framework and Pareto Optimal Front to Calculate Optimal Condition of Ethane Cracking Process

M Farsi^*

Department of Chemical Engineering, Shiraz University, Iran

Submission: June 12, 2019; Published: October 23, 2019

*Corresponding author: M Farsi, School of Chemical and Petroleum Engineering, Shiraz University, Shiraz, Iran

How to cite this article: M Farsi. Integration of Operability Framework and Pareto Optimal Front to Calculate Optimal Condition of Ethane Cracking Process. Recent Adv Petrochem Sci. 2018; 6(5): 555696 DOI: 10.19080/RAPSCI.2019.06.555696

Abstract

The main goal of this research is to present an optimization procedure based on the integration of steady state operability framework and multi-objective optimization concept to find the single optimal solution of processes. To create a quantitative criterion to analysis the performance of chemical processes, the Desired Pareto Index is defined as the ratio of desired Pareto front to the Pareto optimal front. The Desired Pareto Front is defined as a part of Pareto optimal front that all outputs are improved compared to the conventional operating condition. To prove the efficiency of the proposed optimization method, the ethane cracking process is optimized considering feed temperature and steam flow rate as the decision variables. The ethylene production and ethane formation are selected as the main objectives in the developed multi objective model. The simulation results proved the performance of the proposed optimization procedure, so the ethylene production was improved about 3% compared to the conventional condition.

Keywords: Operability framework, Pareto front, Ethane cracking, Mathematical model, Dilution steam, Ethylene, Ethylene oxide, Ethylene dichloride, Polyethylene, Hydrogen productions, Ethyl benzene

Introduction

The main object in the chemical processes is simultaneous capacity and quality enhancement considering the operational, safety and environmental limitations. Usually, this trade-off between the product capacity and quality and developed constraints can be handled by a multi-objective optimization model. Since in the multi-objective optimization problems different and often opposite objectives are simultaneously satisfied, there is a set of optimal points, i.e. Pareto frontier. All points on the Pareto frontier are mathematically equivalent and there is no choice among different solutions on the developed Pareto set [1]. However, from a practical point of view, a system operates at a single point. The selected procedures and decisions in the process design stage have a significant effect on the optimal operability, controllability and plant performance during the process run time. Operability analysis is one of the main bridges between process design and control, which helps the process designer to consider the control issues in the design stage. On the other word, operability analysis is a measuring criterion in modern process control to investigate the ability of a process to operate at an acceptable and safe operating point using the available manipulated variable [2]. Currently, a large number of operability frameworks have been developed to investigate the steady state and dynamic operability of chemical processes. Sharifzadeh presents a good review about developed method to investigate the integration of process design and control [3]. The evolution paths of the methods were described, and the advantages and disadvantages of each method were explained. Subramanian and Georgakis studied the servo, regulatory, and overall operability of CSTR and PFR reactors at steady state condition [4]. It was shown that, it is possible to identify the safe operating points and tolerable disturbances with the available inputs. Ekawati & Bahri [5] proposed a framework based on the integration of the output controllability index and the dynamic operability framework to investigate the controllability and economic assessment of processes. Farsi et al. [6] investigated the steady state operability characteristics of DME reactor using the framework of Vinson and Georgakis. The results showed that the input and output operability index of the process was 43.31% and 57.58% respectively. Santoso et al. [7] investigated the operability of a high-purity distillation column at steady state condition. Based on the simulation results, the safe operating point was obtained and used to provide insights to the operability properties of this highly nonlinear system. Interactions between process units often cause significant difficulties in plant wide control. Ridwan et al. [8] investigated the plant wide operability of a chemical plant unit as a network of process units interconnected with physical mass and energy flow. The plant wide operability analysis was used todetermine the stability and disturbance attainability of Tennessee Eastman Process as a reference system.

Ethylene as the simplest olefin compound is a colorless and flammable gaseous hydrocarbon with a sweet odor. It is produced in the petrochemical industry by thermal steam cracking. The used feedstock varies from ethane, propane to naphtha and gas oil depending on the cost and availability. From practical viewpoint, the ethylene plants are divided into two main sections namely hot and cold sections. In the hot section, the feedstock is fed to a coil furnace and converted to olefin compounds. In the cold section, the outlet product from the furnace is separated and pure ethylene is produced through a sequential distillation column. The produced ethylene is used in the petrochemical plants to produce ethylene oxide, ethylene dichloride, ethyl benzene and polyethylene. Many researchers have focused on the steam cracking process to produce ethylene and propylene. Yancheshmeh et al. [9] modeled ethylene production through thermal cracking of ethane considering steam and carbon dioxide as the dilution. The simulation results showed that the thermal cracking process in presence of CO2 is more effective because of higher ethylene and hydrogen productions and less coke thickness. Keyvanloo et al. [10] modeled and optimized the naphtha steam cracking process based on a multi objective optimization model. Gao et al. [11] developed a mathematical model to investigate the performance of an industrial naphtha cracking process at steady state condition. The optimal temperature and inlet steam to naphtha ratio were found to maximize the operation profit. Masoumi et al. [12] optimized a pilot scale naphtha thermal cracking at dynamic condition. Then, the performance of temperature control loop was tested for different controller parameters and disturbances. Berreni & Wang [13] modeled and optimized propane-cracking process to produce ethylene considering the decoking process at dynamic condition. The tube wall temperature and steam to propane ratio in the feed were used as decision variables. Dynamic optimization indicated that the obtained optimal operating points can improve profit about 13.1%.

In this paper, an efficient integration between operability framework and Pareto based multi-objective optimization is proposed to calculate the optimal condition of ethane cracking process. In section 2, the proposed operability-based optimization framework, operability index and the optimal Pareto front are explained. In section 3, the considered kinetic model, assumptions and developed mathematical model of the ethane cracking process is presented at steady state condition. In section 4, the simulation results are presented and compared with the base case at steady state condition.

Optimization Framework

Operability index

In this section, the operability framework introduced by Vinson & Georgakis is reviewed [14]. In this framework, the available process inputs that change over a certain range are calledAvailable Input Space (AIS). The mathematical model of process is solved in range of AIS to obtain the available outputs. The calculated available output points are referred to as the achievable output space (AOS). In addition, Desired Output Space (DOS) is specified as the desired process outputs by operator. The set of input variables required to obtain DOS can be calculated from the model inverse. The required input values are denoted as the desired input space (DIS). The Output and Input Operability indexes are defined as:

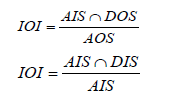
OOI index indicates that how much of the desired process outputs are in the range of available outputs. Also, IOI index indicates that how much of the inputs are available to create DOS. The main challenge in the operability analysis is to determine the DOS region in a chemical process. Generally, the DOS is determined by the plant operators.

Multi-objective optimization

Multi-objective optimization is a mathematical procedure, which a number of objective functions are simultaneously optimized. This problem is mathematically formulated as:

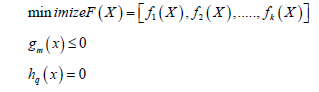
Where, K, m and q are the number of objectives, inequality and equality constraints, respectively. In the problem consists contradictory objective functions, the single-objective optimization presents an unacceptable solution. The multi-objective approaches allow decision making to think about the trade-offs between different objects. Multi-objective optimization problems satisfy a number of different and even contradictory objectives, which is known as Pareto optimal solutions [15]. For a given Pareto optimal set, the corresponding objective function values in the objective space are called the Pareto frontier. The vector is a Pareto optimal solution if there does not exist another in the feasible search region such that * i i f x f x → →   ≤       for all ∈{1, 2,...., k} and * i i f x f x → →   <       for at least one ∈{1,2,...., k} . Indeed, all points on the Pareto set are mathematically equivalent and the decision-maker decides which one of obtained design vectors is appropriate. The main challenge in the multi objective optimization is the range of input variables. Generally, the single optimal point is selected from developed Pareto front by decision making method. The variation of the range of input variables changes the length of Pareto front, and the different single optimal point is obtained by the decision-making methods.

Developed framework

In this section, the proposed framework to find the single optimum operating condition of a conventional process is explainedconsidering a multi-objective function. In multi input-output systems, the output states are developed based on the available inputs considering steady state mathematical model of process and the Pareto optimal front is determined based on the calculated outputs. A solution is called Pareto optimal curve, if none of the objective functions can be improved in value without degrading some of the other objective values. The Desired Pareto front is defined as a part of developed Pareto optimal front that all of outputs presents the better performance compared to the conventional condition. This index indicates how much of the developed Pareto optimal front is completely desirable and achievable with the available inputs compared to the current operating condition. Then, the Desired Pareto Index is defined as the ratio of developed desired Pareto front to the Pareto optimal front.

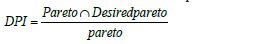
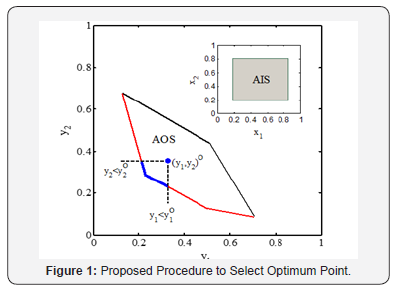
For illustration, consider a continuous process with two inputs, and and two outputs and , respectively (Figure 1). shows the AIS and the calculated AOS based on the AIS. The Pareto front, red line, is determined based on the AOS to minimize and , respectively. Since process operates at a single operating point, one of the points on the Pareto front should be selected as the single optimal point. The conventional operating point of the process is determined on the AOS as . Desired Pareto front, blue line, is defined as the operating points that minimize and simultaneously and preferred to the conventional operating point [16]. Indeed, the surrounded surface by , and Pareto front is the DOS. In two-dimensional case, when the length of desired Pareto front approaches to the Pareto front curve, the Desired Pareto Index approaches toward one. It proves that the conventional operating point is far from optimal condition and process operates at non-optimal condition. In case that operating point takes place on the Pareto front, the desired Pareto front is a single point and Desired Pareto Index approaches toward zero. It proves that the process operates at an optimal condition. Indeed, the proposed method limits the length of Pareto front based on the conventional operating point and helps the decision maker to select a single optimal point based on the conventional operating point.

Process Modeling

Process description

Thermal cracking process is one of main method to produce olefins such as ethylene and propylene. In the ethane cracking process, the feedstock is heated to 750-850°C in a furnace to crack the ethane into ethylene. Steam is mixed with the feedstock to reduce coking rate and improve the product yield. The cracking reactions occur at a short residence time and high temperature, followed by a sudden quench to stop reactions. This is followed by product fractionation, which includes distillation, and other processes to separate products and unreacted reactants. Then, ethane is recycled and fed to the furnace. Thermal cracking of hydrocarbons accompanies coke formation and deposition over the inner surface of coil tube. Coke formation reduces heat flux from combustion chamber to the reactor and creates an extra heat resistance in the tube. To keep the heat transfer in the desired level and increasing the process capacity, the skin temperature should be raised. Generally, it decreases ethylene selectivity and increases maintenance and utility costs. Thus, the plant shifts to shut down for decoking process after 30–90 days. The decoking process is carried out by burning the coke using a mixture of air and steam.

Kinetic modeling

The ethane cracking reactions can be divided as primary thermal cracking, secondary thermal cracking, dehydrogenations, and cyclization of butadiene and ethylene and coke formation reactions. The high temperature and long residence time should be avoided to prevent the coke formation. The main reactions in the thermal cracking of ethane are as follows [9,16]:

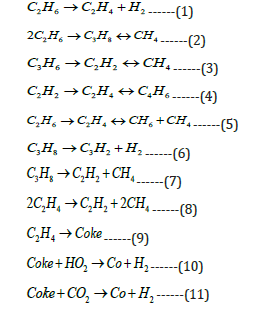
The reaction equilibrium constants and Arrhenius kinetic parameters are taken from literature [9].

Process model

In this section, the mass and energy balances are developed. The considered assumptions to simplification of the model are as follows:

a) The gas mixture is an ideal gas.

b) The radial gradients such as mass, heat and concentration are neglected.

c) Quasi-steady state is assumed to simulate the coke deposition rate.

d) Plug flow pattern is employed

The mass and energy balances in coil tube can present as:

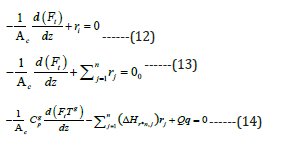
The reaction equilibrium constants and Arrhenius kinetic parameters are taken from literature [9].

Process model

In this section, the mass and energy balances are developed. The considered assumptions to simplification of the model are as follows:

b) The radial gradients such as mass, heat and concentration are neglected.

c) Quasi-steady state is assumed to simulate the coke deposition rate.

d) Plug flow pattern is employed.

The mass and energy balances in coil tube can present as:

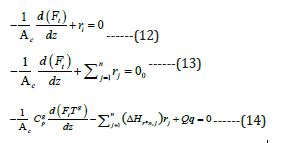
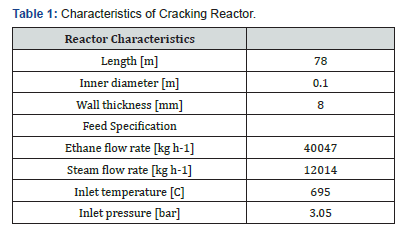
In addition, suitable temperature and component dependent correlations are chosen to estimate the physical properties of components and mixture such as viscosity, specific heat capacity, heat conductivity and diffusion coefficients. Table 1 shows the reactor characteristics and feed specification of a domestic industrial ethane cracking.

Results and Discussion

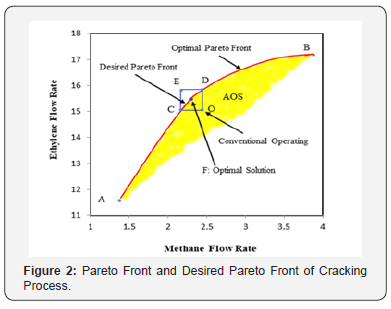
In this work, the cracker is modeled, and optimal feed temperature and steam flow rate are obtained by integration of operabilityframework and optimal Pareto front. Then the process performance at the optimized condition is analyzed at steady state condition. The considered objective functions, maximum ethylene production and minimum methane formation, forms a multi-objective problem. To analyze the steady state operability of the cracking process, steam flow rate and feed temperature are considered as the input variables. The steam rate changes in rang of 10-20 moles-1 and feed temperature in rang of 875-905 K, respectively (Figure 2). shows the calculated AOS against considered AIS based on the developed mathematical model. This figure shows that at maximum ethylene production, point B, the maximum methane is produced. In addition, the minimum ethane production occurs in point A, that ethylene is at minimum rate. In the AOS domain, Line AB and point O present the Pareto optimal front and conventional operating point in the ethane cracking process, respectively. The operating points online CD as a part of Pareto front improve all objective functions compared to the conventional operating point, O, and defined as the desired Pareto front. The calculated Desired Pareto Index is about 0.12 in the considered cracking process and proves that there is some operating point to improve plant performance considering available input variables. It was mentioned that in two-dimensional case, that operating point approaches toward the developed Pareto front, the Desired Pareto Index approaches toward zero and the process operates at the optimal condition. Generally, this approach helps operator to select a single optimal point from developed desired Pareto front. In this research, the single optimal point is selected from desired optimal front based on the TOPSIS decision-making method. The TOPSIS is a distance based decision-making method that recommends the solution with minimum distance from ideal solution and maximum distance from non-ideal solution [17].

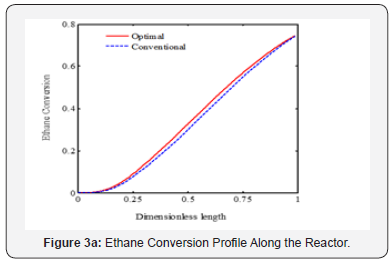
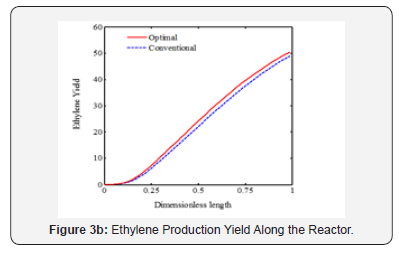
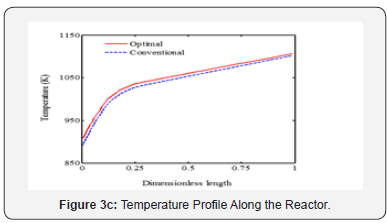
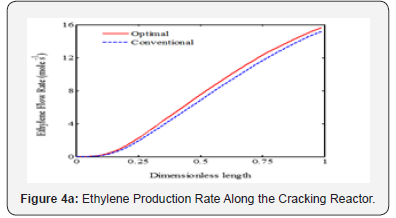
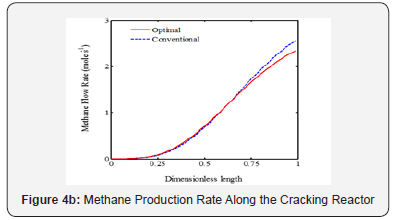
It is appeared from (Figure 2). that points E and O are ideal and non-ideal solutions, respectively. Since the conventional operating point, O, has been considered as non-ideal solution, the selected optimal solution presents the better plant performance. The point F has been proposed by TOPSIS method as the single optimal solution of the ethane cracking process. The produced ethylene and methane at the optimal process are 15.62 and 2.34 moles-1, respectively. It is appeared that the ethylene production is improved about 3%, while methane production decreased 8.9%compared to the conventional operating point. It is appeared that the integration of operability and multi objective optimization and considering conventional operating point as a reference limit the length of Pareto front and help the decision maker to select a single optimal point based on the conventional operating point (Figure 3a-c). shows the ethane conversion, ethylene production yield and temperature profiles along the reactor. It is appeared that difference between ethane conversion in conventional and optimal systems is negligible, while ethylene yield is improved about 3%. It proves the feasibility and optimality of the selected solution against the conventional condition. Although the cracking reactions are endothermic, the higher heat transfer from combustion chamber to the coil tube compared to the heat consumption through the endothermic cracking reactions results in a rising temperature profile in the reaction zone (Figure 4a-b). shows the ethylene and methane production rate along the cracking reactor at steady state condition. This figure shows that ethylene mole flow rate increases along the reactor and approaches toward 15.62 mole s-1 in the optimized condition. Generally, there is a considerable difference between the performance of conventional and optimal systems to produce methane and ethylene. Generally, the higher temperature in the optimized system could increase the rate of cracking reactions. On the other hand, the ethane cracking to methane is a second order while, the ethane to ethylene cracking reaction is first order compared to the ethane concentration. Thus, the higher rate of dilution steam in the optimized condition and decreasing ethane concentration along the reactor have a significant effect on the reactions and results in the lower ethane to methane conversion (Figure 5). shows the coke thickness profile along the reactor. At high temperatures, residence time, and low steam to hydrocarbon ratio, coking rate increases and formed coke is deposited on the tube internal walls. In the ethane steam cracking plant, a part of produced olefins is converted to coke and deposited on the coil tube as the skin. The formed coke decreases the heat transfer coefficient between combustion chamber and reaction zone and results in the higher fuel consumption in the chamber and tube wall temperature. When maximum tube surface temperature is obtained, the process is shut down and decoking cycle is started. In addition, because of coke formation, the effective inner tube diameter decreases and results in a higher pressure drop.

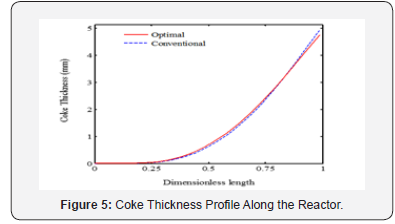
Dilution steam decreases hydrocarbon concentration in the reaction zone and results in lower coke formation. On other hand, coke is converted to synthesis gas, hydrogen and carbon monoxide, through steam reforming reaction. Thus, a part of produced coke is removed through the steam reforming. The results show that maximum coke thickness has been decreased about 3.8% in the optimized plant compared to the conventional system.

Conclusion

In this research a quantitative criterion was developed to analysis the performance of chemical process based on the integration of the operability framework, Pareto optimal front and conventional operating point. The single optimal operating was calculated by the TOPSIS decision making method based on the developed Desired Pareto front. It was shown that the proposed method limits the length of Pareto front based on the conventional operating point and helps the decision maker to select a single optimal point based on the conventional operating point. Then, the ethane steam cracking process was selected as a reference model to investigate the performance of the proposed optimization method. The simulation results showed that ethylene production is improved about 3% and methane production decreased 8.9% compared to the conventional operating point.

References

1. Deb K (2014) Multi-objective optimization. Search methodologies, Springer, pp. 403-449.
2. Skogestad S, Postlethwaite I (2007) Multivariable feedback control: analysis and design. Wiley New York, USA.
3. Sharifzadeh M, (2013) Integration of process design and control: A review. Chemical Engineering Research and Design 91(12): 2515-2549.
4. Subramanian S, Georgakis C (2001) Steady-state operability characteristics of idealized reactors. Chemical engineering science 56(17): 5111-5130.
5. Ekawati E, Bahri PA (2003) The integration of the output controllability index within the dynamic operability framework in process system design. Journal of Process Control 13(8): 717-727.
6. Farsi M, Mazinani S, Jahanmiri A (2011) Steady state operability characteristics of an adiabatic fixed-bed reactor for methanol dehydration, Iran. J Chem Chem Eng Research Note 30(4).
7. Santoso H, Rojas OJ, Bao J, Lee P (2007) Nonlinear process operability analysis based on steady-state simulation: a case study. Chemical Product and Process Modeling 2(2).
8. Setiawan R, Hioe D, Bao J Plantwide operability analysis based on a network perspective A study on the Tennessee Eastman process Proc. Dynamics and Control of Process Systems 451-456.
9. Yancheshmeh MS, Haghighi SS, Gholipour M, Dehghani O (2013) Modeling of ethane pyrolysis process A study on effects of steam and carbon dioxide on ethylene and hydrogen productions. Chemical Engineering Journal 215: 550-560.
10. Keyvanloo K, Towfighi J, Sadrameli S, Mohamadalizadeh A (2010) Investigating the effect of key factors their interactions and optimization of naphtha steam cracking by statistical design of experiments. Journal of Analytical and Applied Pyrolysis 87(2): 224-230.
11. Gao GY, Wang M, Ramshaw C, Li XG (2009) Optimal operation of tubular reactors for naphtha cracking by numerical simulation. Asia‐Pacific Journal of Chemical Engineering 4(6): 885-892.
12. Masoumi M, Sadrameli S, Towfighi J, Niaei A (2006) Simulation optimization and control of a thermal cracking furnace Energy 31(4): 516-527.
13. Berreni M, Wang M (2011) Modelling and dynamic optimization of thermal cracking of propane for ethylene manufacturing. Computers & Chemical Engineering 35(12): 2876-2885.
14. Seferlis P, Georgiadis MC (2004) The integration of process design and control. Elsevier.
15. Madetoja E, Ruotsalainen H, Mönkkönen VM, Hämäläinen J, Visualizing multi-dimensional Pareto-optimal fronts with a 3D virtual reality system Proc. Computer Science and Information Technology (2008) IMCSIT (2008). International Multiconference on IEEE 907-913.
16. Zou R, Lou Q, Mo S, Feng S (1993) Study on a kinetic model of atmospheric gas oil pyrolysis and coke deposition. Industrial & engineering chemistry research 32(5): 843-847.
17. Etghani MM, Shojaeefard MH, Khalkhali A, Akbari M (2013) A hybrid method of modified NSGA-II and TOPSIS to optimize performance and emissions of a diesel engine using biodiesel. Applied Thermal Engineering 59(1): 309-315.