Research Article

Robot Path Estimation from Odometry Measurements: Loop Closure Based on Autocorrelation

Spyridon Garmpis¹, Evangelos Dermatas¹ and Aristogiannis Garmpis²*

Signal Processing and Communications Lab, department of Computer Engineering and Informatics, University of Patras, Greece

Submission: November 04, 2022; Published:November 14, 2022

*Corresponding author: Evangelos Dermatas, Signal Processing and Communications Lab, department of Computer Engineering and Informatics, University of Patras, Greece

How to cite this article: Garmpis S, Dermatas E, Garmpis A. Robot Path Estimation from Odometry Measurements: Loop Closure Based on Autocorrelation. Robot Autom Eng J. 2022; 5(3): 555662. DOI: 10.19080/RAEJ.2022.05.555662

Abstract

The problem of estimating the Robot path when covering closed trajectories using only the wheels odometry information is met in indoor low-cost robotic applications. Random and systematic errors related to the measured angle accuracy, deviations from the desired path and wheel radius in robot turns, introduced significant errors in the process of estimating the actual path. In this paper the autocorrelation function is used for accurate estimation of the path periodicity and to reconstruct the robot path. Real-life experiments using a real robot showed minor differences between the estimated and the predicted path.

Keywords: Loop closure; Periodicity Detection; Autocorrelation; Path Estimation; Wi-fi Localization

Abbreviations: EKF: Extended Kalman Filter; SLAM: Simultaneous localization and mapping

Introduction

Indoor robotics is a recently developed research area which has entered the industry with quite a rapid rate. The reason for this is the huge amount of attention that wireless sensor networks [1] and autonomous vehicles [2] have drawn. An intuitive problem that has arisen is the precise localization of the robots, due to the small size of the indoor environment that they act in. Many techniques have been proposed for indoor localization but the most active is the one based on Wi-Fi [3].

Another essential parameter for localization is the knowledge of the robot’s environment (map). SLAM constructs the environment structure, a two- or three-dimensional map synchronously with the estimation of the robot’s position while moving in it. A typical SLAM system consists of two main components: the front-end process associates the sensor’s data to the partially constructed map distances i.e., those that have been already observed, while the back-end module completes new parts of the map by applying optimization techniques [4, 5]. The so-called graph-SLAM [6], connects the two modules through a factor graph [7]. Front-end module accounts for the building of the factor graph based on all the available information and afterwards, the back-end module, translates this graph into an optimization problem to perform the optimal estimation of the final map that this graph represents.

The formulation of the optimization problem was first considered by [8, 9] who set the bases for modeling the spatial relationships of the problem and solved it optimally. The enhanced optimization methods based on maximum likelihood estimation are [10-14], which in contrast to Kalman filters does not need a model that describes the system under consideration. Some other techniques based on EKF or windowing [15-16] and nonlinear filtering or smoothing [17-18] have been applied.

In the case where the robot performs a repeated trajectory, i.e., line-following in a close path, one of the front-end data association tasks is the loop closure. Loop closure is a mechanism that eliminates the accumulative uncertainty of the robot’s pose by recognizing areas that have already been visited [19]. This problem has been solved by many researchers [20-22] by adding some unique points throughout the path and detecting them using cameras or other distance measurement systems, such as lidar, ultrasonic, phototransistors sensors [23].

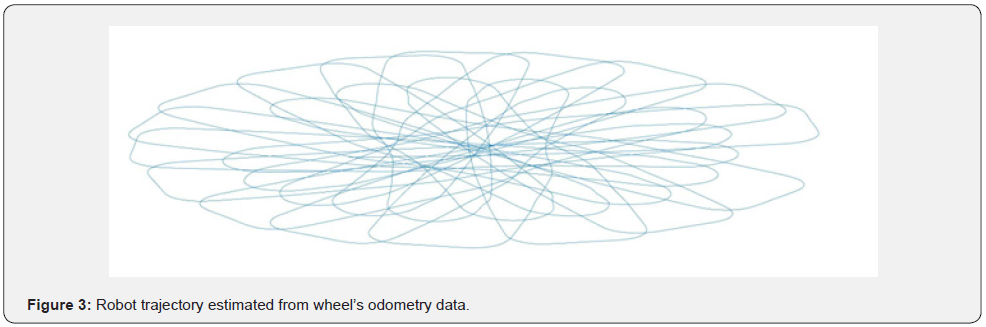
The estimation of a robot position using only odometry information i.e., wheels’ angle as a function of time, is a difficult task due to the errors introduced by the sensor’s accuracy, deviations from the desired path and the variability of the wheel’s radius during robot movements. In the special case where the robot performs multiple loops in the same path, the fact of repeated passage from the same positions in space can be used to decrease the influence of both systematic and stochastic errors in the process of estimating the robot position. As shown in figure 1, the estimated trajectory using the raw odometry data, results in the increment of the difference between the actual and the real robot position at each step [24, 25]. The resulting trajectory is a gradually shifted repetition of the actual closed path that the robot follows [26]. So, the main problem is to derive a method to correct the unbounded accumulated error [30] [35] which causes this deviation from the real path.

According to [27] a piecewise linear function of the accumulative wheel angle displacement can be used for the detection of the loop closure points by creating an error matrix of the mean distance of some linearly distributed points for every node of the graph and finding local minima of this error matrix. Afterwards, the nodes that correspond to detected loop closures are connected with an edge of the graph and the Levenberg- Marquardt optimization algorithm [12] is applied for the estimation of the final map.

This article was inspired by [27] improving the estimation accuracy of the loop closure period. Instead of using a piecewise linear function for the detection of the loop closing constraints, the proposed method faces this problem from a signal processing point of view. The implemented idea is that, if the periodicity of the robot’s trajectory is found, it can be used to create loop closing points and will enable the merging of all the recurrent trajectories around the main map.

Materials

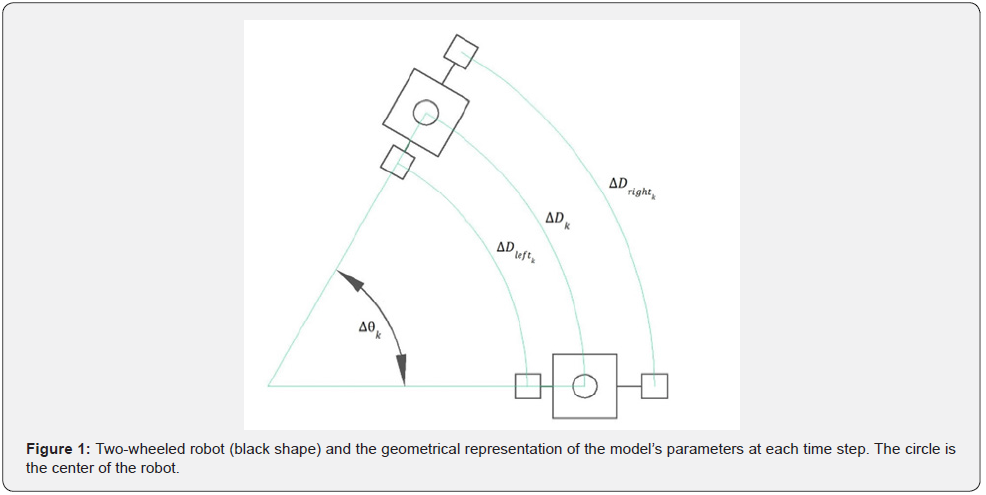
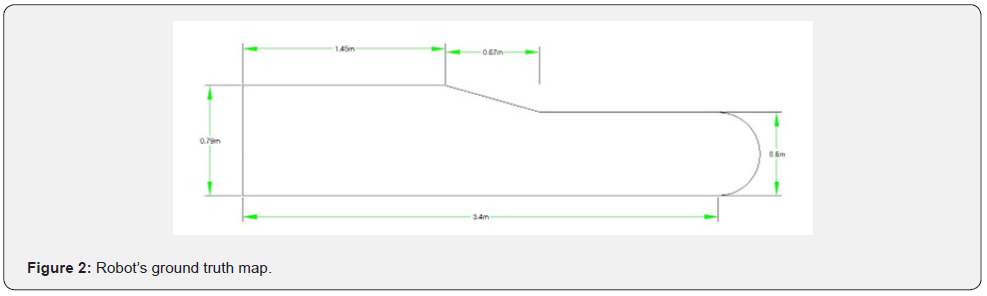
The experimental set up consists of a two wheeled EV3 robot manufactured by LEGO, equipped with two color sensors. The wheel radius was 2cm, and the distance between the two wheels was 13.5cm. A simple line following. a sensor’s acquisition module and a Bluetooth data transfer process was implemented, downloaded and executed in the robot processor unit as two independent tasks. In (Figure 1) the visual line embedded on the floor and the actual distances are shown.

The transmitted record acquired by the robot sensors is constituted by six fields: Increasing measurement number, robot time in ms, current left wheel angle in degrees, current right wheel angle in degrees. A typical example of the data sequence created by the EV3 is: “6,50747,447, 448”. A serial Bluetooth data exchange protocol was implemented between the EV3 and a Raspberry Pi 3 model B+ single board computer performing realtime data transmission at a rate of 3-4 records per second. The data set created to evaluate the proposed method, consists of 10 Files, including 7200 measurements and acquired in a time period of 31 minutes.

Methods

If wheel radius is r and the distance between the two wheels is L, the path covered by robot’s right wheel, , is given by the relation , if the current right wheel angle is . A similar equation estimates the corresponding path covered by the left wheel, i.e., .

At every time sample k, the wheels distance between the current and the previous sample can be derived by

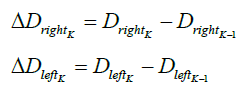
Taking into account the robot model of figure 2, the robot’s center position, in the 2-D plane with coordinates at each time sample, can be estimated by,

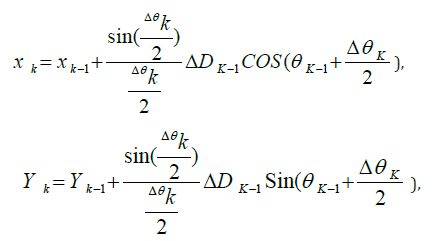
where, x_k, y_k and θ_k is the position and the orientation of the robot respectively and

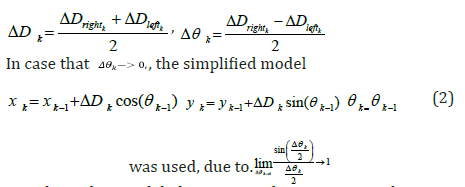
Based on this model the estimated trajectory is shown in figures 2, 3.

According to Rottmann, N. et al. [27]. The path estimation process is splitted into a set of sequentially connected modules. Initially, a path segmentation module is used to cluster the individual path points retrieved from the odometry data into straight line segments. In our implementation the complete set of data points derived by eq. (1) or (2) (these are equations) has been used to build the path points. In the adopted method the created map is more accurate, and the additional computational complexity is not important in our approach because the mapping estimator is an offline process.

Subsequently, the loop closure detection module undertakes to search for poses with similar shaped neighborhoods in order to find vertices which can be matched onto each other. For these matched vertices a connection in the pose graph is added. For this process, a piecewise linear function is created which accumulates the difference of the wheel’s angle between two successive positions of the robot. An error matrix measures the distance between the shapes of the neighborhood positions using the introduced piecewise orientation function. In our approach, the period of the robot’s trajectory is used to detect similar shaped neighborhoods in order to detect vertices which can be matched onto each other. For the estimation of the robot’s trajectory period, only the difference of the wheel’s angle between two successive robot positions is used

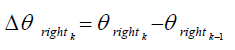
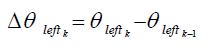
Among the digital signal processing methods that detect signal periodicity, the autocorrelation method [28] is robust in random noise but sensitive to DC noise. In this article the periodicity of the close loop trajectory is estimated by the autocorrelation method of the wheel’s angle difference

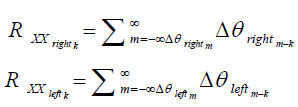
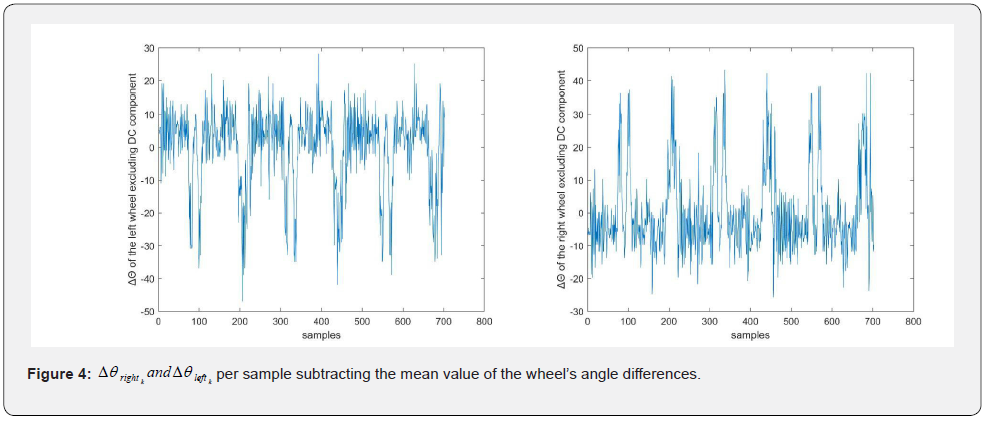
Before autocorrelation is used, the mean value of the signal must be subtracted to increase the variance of the autocorrelation function (Figure 4). enhancing also the detection accuracy of the desired maximum points, as shown in figure 5. It is well known that the signal periodicity can be detected at the local maxima of the autocorrelation function.

When the loop closure detection module is completed, the resulting graph, which consists of the sequential connection of the nodes that represent the states of the robot and the connection of the nodes that represent the matched vertices, is subjected to pose graph optimization. The optimization problem that this module solves is based on the minimization of a weighted sum of the measurement’s errors, where the covariance matrix is derived by the robot’s model.

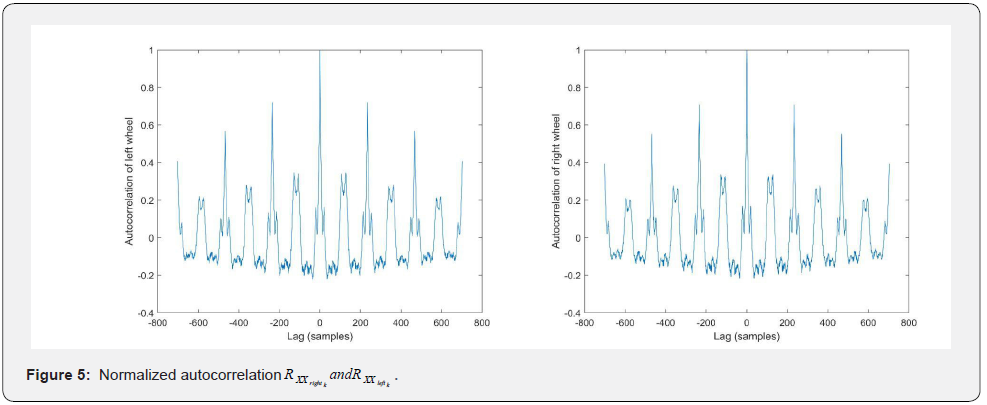
The maximum value observed at the center of the function corresponds to the energy of the signal, which is equal tο one, due to normalization. The periodicity of the considered signal for each wheel is equal to the sample time that the first maximum of the autocorrelation function is met, excluding the one at the center of the function.

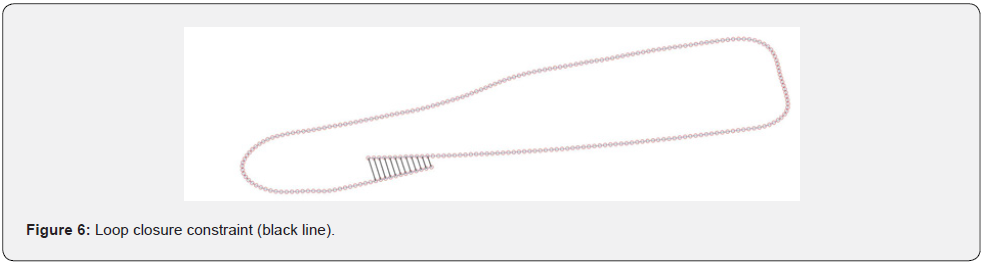
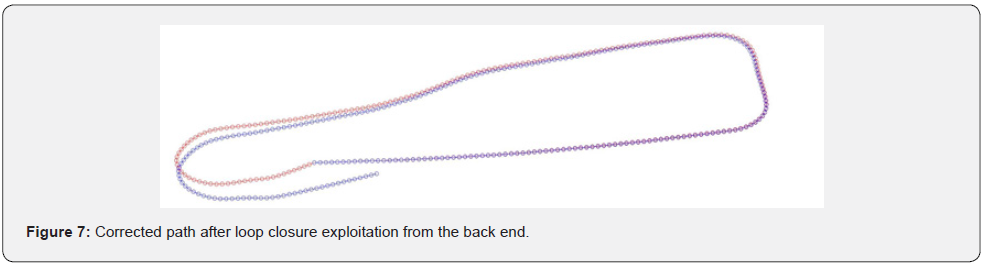
The detection of the signal period signifies that the sample at which the period was completed is a new measurement of the robot’s starting position. According to this, these two different states that occur in the estimation map represent the same position. Therefore, these vertices are matched by adding a connection in the pose graph between their corresponding nodes, as can be seen in figure 6. Following this procedure, every upcoming node can be connected with the following node starting from the first and when an integer multiple of the period sample is reached a third layer of connections can be added to the first node. In figure 6, only twelve of those connections are drawn in order to illustrate the main idea clearly. Sequentially, the pose graph optimization problem was created according to [27] and [12] which led to the final map of of Fig. 7 (red trajectory) by applying the Levenberg–Marquardt algorithm for solving the weighted nonlinear least squares optimization problem.

Results and Discussion

Appling the above methodology, after normalization, on both the left and the right wheel’s angle displacement, lead to the number of samples at which the path of the robot is repeated, number of samples = 234. This can be verified by the estimation of the period, period = 59026ms, which is approximately equal to number of samples * sampling time = 234 *250 ms = 58s. As shown in figure 5, the local maximum values of the function that correspond to the loop closure points are conspicuous and integer multiple of 234. Moreover, there is no need to apply more sophisticated periodicity estimation algorithms due to the high accuracy of the results, shown in table 1 & 2. Finally, the error from the ground truth has decreased due to the incorporation of the loop closure constraints in the optimization problem of the back-end mechanism. This improvement can be seen in the comparison of the pure odometry-based map (blue trajectory in map (blue trajectory in Fig. 7) with the optimization-based map map (red trajectory in Fig. 7). Given the loop closing constraints, an optimization problem can be formulated according to [27]. which can lead to the map estimation estimation. Fig. 6, illustrates the points that correspond to the same position when one loop is completed.

Future research

The direction of this work will be to decrease the estimation error for both indoor and outdoor localization applications. This will be achieved by equipping the wheeled robot with more sensors which will provide more information to build the SLAM optimization problem. More precisely, acoustic, and light sensors can be used to measure the distance of the nearby objects and the brightness variation of the ground. To incorporate these signals, some fusion algorithms will be implemented. Additionally, computational models can be combined with the sensors, potentially leading to a more accurate and robust mapping of the robot’s trajectory. Computational models behave as virtual sensors providing even more information about the system’s states [29].

Conclusion

This article proposes a method to estimate a closed path from multiple passes of a robotic vehicle using only odometry information from wheel angle. The detection on the signal’s period was precise and can potentially lead to the increment of the estimated map accuracy. This technique will be incorporated in cases where accurate robot position is required in low-cost indoor robot implementations.

References

1. Huang BJ, Zhao J, Liu (2019) A Survey of Simultaneous Localization and Mapping with an Envision in 6G Wireless Networks. ArXiv: 1909.0521.
2. Takleh TTO (2018) A Brief Survey on SLAM Methods in Autonomous Vehicle. International Journal of Engineering & Technology 7(4.27): 38-43.
3. Zafari F A, Gkelias K, Leung (2017) A survey of indoor localization systems and technologies. IEEE Communication Surveys & Tutorials 21(3): 2568-2599.
4. Niko Sunderhauf (2012) Robust Optimization for Simultaneous Localization and Mapping.thesis Chemnitz University of Technology.
5. Sualeh M, Kim GW (2019) Simultaneous Localization and Mapping in the Epoch of Semantics: A Survey International Journal of Control Automation and Systems 17(3): 729-742
6. Latif Y, Cadena C, Neira J (2013) Robust loop closing over time for pose graph slam. The International Journal Robotics Research 32(14): 1611-1626.
7. Kschischang FR, Frey BJ, Loeliger HA (2001) Factor graphs and the sum-product algorithm. IEEE Transaction on Information Theory 47(2): 498-519.
8. Lu FE, Milios (1997) Globally consistent range scan alignment for environment mapping. Autonomous Robots 4: 333-349.
9. S. Gutmann, K. Konolige (1999) Incremental mapping of large cyclic environments. IEEE International Symposium on Computational Intelligence in Robotics and Automation USA.
10. Grisetti GR, Kummerle C, Stachniss W, Burgard (2010) A tutorial on graph-based SLAM. IEEE Intelligent Transportation System Magazine 2(4): 31-43.
11. Kuemmerle RG, Grisetti H, Strasdat K, Konolige W, Burgard (2011) G2o: A general framework for graph optimization. IEEE International Conference on Robotics and Automation China.
12. Grisetti G, Kümmerle R, Stachniss C, Frese, Hertzberg C (2010) Hierarchical optimization on manifolds for online 2D and 3D mapping. IEEE International Conference on Robotics and Automation (ICRA) USA.
13. Dellaert F, Kaess M (2006) Square root SAM: Simultaneous localization and mapping via square root information smoothing. The International Journal on Robotic Research 25(12): 1181-1203.
14. Thrun S, Montemerlo M (2006) The GraphSLAM algorithm with applications to Large-Scale mapping of urban structures. The International Journal of Robotic Research 25(5-6): 403-430.
15. Huang GP, Mourikis SI, Roumeliotis (2011) An observability constrained sliding window filter for SLAM. IEEE/RSJ International Conference on Intelligent Robots and Systems, USA.
16. Mourikis AI, Roumeliotis SI (2007) A Multi-state constraint Kalman filter for vision-aided inertial navigation. IEEE International Conference on Robotics and Automation, Italy.
17. Bailey T, Durrant-Whyte HF (2006) Simultaneous localisation and mapping (SLAM): Part II. IEEE Robotics and Automation Magazine 13(3): 108-117.
18. Strasdat H, Montiel JMM, Davison AJ (2012) Visual SLAM: Why filter. Image and Vision Computing 30(2): 65-77.
19. Cadena C (2016) Past present and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Transactions on Robotics 32(6): 1309-1332.
20. Lowry S (2016) Visual place recognition: A survey. IEEE Transactions on Robotics 32(1): 1-19.
21. Newman P, Leonard JJ, Tardos JD, Neira J (2002) Explore and Return: Experimental validation of Real-Time concurrent mapping and localization. IEEE International Conference on Robotics and Automation USA.
22. Huang BJ, Zhao J, Liu (2019) A Survey of Simultaneous Localization and Mapping. ArXiv: 1909.05214.
23. Wang CM (1988) Location Estimation and Uncertainty Analysis for Mobile Robots. IEEE International Conference on Robotics and Automation USA Pp. 90-95.
24. Chong KSL, Kleeman (1997) Accurate Odometry and Error Modelling for a Mobile Robot. International Conference on Robotics and Automation USA.
25. Kelly A (2013) Mobile Robotics: Mathematics Models and Methods. (First Edition) Cambridge University Press Cambridge. UK.
26. Rodríguez-Arevalo ML,Neira JJ, Castellanos A (2018) On the Importance of Uncertainty Representation in Active SLAM. IEEE Transactions on Robotics 34(3): 829-834.
27. Smith RM, Self P, Cheeseman (1988) Estimating Uncertain Spatial Relationships in Robotics. Machine Intelligence and Pattern Recognition Pp. 167-193.
28. Rottmann NR, Bruder A, Schweikard E, Rueckert (2019) Loop Closure Detection in Closed Environments. European Conference on Mobile Robots (ECMR) Czech Republic.
29. Sands T (2021) Virtual Sensoring of Motion Using Pontryagin’s Treatment of Hamiltonian Systems. Sensors 21(13): 4603.
30. Frank Kurth (2013) The shift-ACF: Detecting multiply repeated signal components. IEEE Workshop on Applications of Signal Processing to Audio and Acoustics USA Pp. 20-100.
31. Grisetti G, Stachniss C, Grzonka S, Burgard W (2007) A tree parameterization for efficiently computing maximum likelihood maps using gradient descent. Robotics: Science and Systems III USA.
32. Kaess M (2011) iSAM2: Incremental smoothing and mapping using the Bayes tree. The International Journal of Robotics Research 31(2): 216-235.
33. KOlson E, Leonard JJ, Teller S (2006) Fast iterative alignment of pose graphs with poor initial estimates. IEEE International Conference on Robotics and Automation USA.  
34. Hesch JA, Kottas DG, Bowman SL, Roumeliotis SI (2013) Camera-IMU-based localization: Observability analysis and consistency improvement. International Journal of Robotic Research 33(1): 182-201.
35. Hesch JA, Kottas DG, Bowman SL, Roumeliotis SI (2014) On the consistency of vision-aided inertial navigation. IEEE Transactions on Robotics. Pp. 303-317.
36. Durrant-Whyte HF, Bailey T (2006) Simultaneous localisation and mapping (SLAM): Part I IEEE Robotics and Automation Magazine 13(2): 99-110