Geometric Simulation for 3D-Printed Soft Robots
Tsz Ho Kwok*
Department of Mechanical, Industrial and Aerospace Engineering, Concordia University, Canada
Submission: December 04, 2018; Published: December 17, 2018
*Corresponding author: Tsz Ho Kwok, Department of Mechanical, Industrial and Aerospace Engineering, Concordia University, Canada.
How to cite this article: Tsz Ho K. Geometric Simulation for 3D-Printed Soft Robots. Robot Autom Eng J. 2018; 4(1): 555630. DOI: 10.19080/RAEJ.2018.04.555630
Introduction
Robots fabricated by soft materials can provide higher flexibility and thus better safety while interacting with natural objects with low stiffness such as food and human beings. With the growth of three-dimensional (3D) printing, it is even possible to directly fabricate soft robots [1,2] with complex structures and multiple materials realizing highly dexterous tasks like human-interactive grasping and confined area detection [3]. However, with such increased degrees of freedom (DoF), the design of soft robots becomes a very difficult task. It can be made possible by integrating simulation into the design phase. However, the shape deformation comes from many different and complex factors including manufacturing process, material properties, actuation, etc. Especially with the limited understanding of layer-based additive process in AM, it is challenging to formulate a complete mathematical model for the simulation.
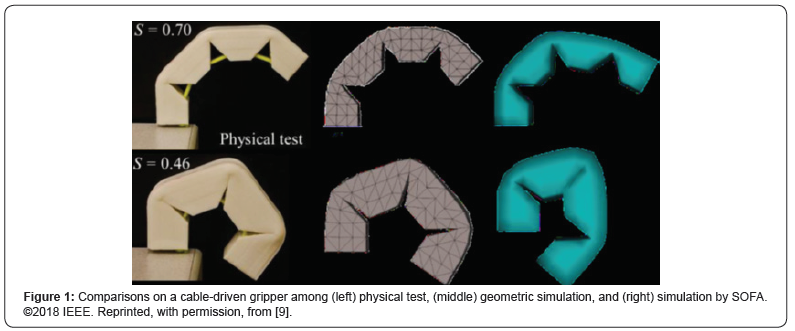
SOFA [4] is one of the most widely used frameworks for physical simulation. It is also applied in the simulation of soft robots that supports interactive deformation [5]. However, it may suffer from the problem of numerical accuracy, particularly if there is large deformation. Unfortunately, one benefit of soft robot is its capability of adapting to highly curved contact by large deformation, which needs to be precisely simulated for many applications. There is another type of simulation methodology to simplify the simulation model of deformation to a geometry optimization problem [6]. It was originally developed in the computer graphics area for visualization, but it has been proved to work superbly in physical simulation like self-transformation structures [7] and the computational efficiency is remarkable [8]. This geometric simulation is particularly suitable for soft robots [9] (Figure 1), because the actuation of soft robots is commonly defined by geometry variations (e.g., cable shortening and pneumatic expansion), and it is actually indirect to first obtain apply them in the conventional deformation simulation. It is shown that the geometric simulation gives better convergence and accuracy than the conventional methods. Therefore, the aim of this review is to share this technique with a broader audience in the robotic community, and discuss the potentials capabilities, and future works of this technology.
Geometric Simulation
The common way of Finite Element Analysis (FEA) is to apply Hooke’s law to each element and then assemble the equations to compute the deformation with the applied force:
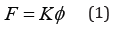
where 𝐹 is the global nodal force vector, 𝐾 is the global stiffness matrix, and 𝛷 is the global nodal displacement vector. In the geometric simulation, the formulation is developed by shape projection on the elements in terms of point positions:
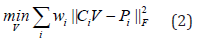
where 𝐕 ∈ ℛ𝑛×3 stacks all the point positions of 𝑛 vertices, Ci ∈ ℛ𝑒×𝑛 is the centering matrix for the 𝑖-th element among 𝑒 elements, Pi ∈ ℛ 𝑒×3 is the variables defining the shape projections for the element, and 𝑤𝑖 is the weight for the element, which is commonly set as the volume. This minimization can be solved by taking derivative and thus a sparse symmetric positive definite system:
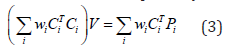
This geometric optimization is formulated to minimize the elastic energy with reference to shape variations similar to the physical phenomenon during deformation. To compare Eq. (3) with Eq. (1), they have the same form with:
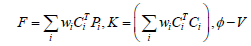
Therefore, the geometric simulation actually has the benefits as the FEA, but it should be noted the force vector 𝐹 here is defined purely by the shape projections. As a result, this is a direct approach to take the geometric actuation as input and compute the deformed shape of soft robots by numerical optimization using a geometry-based algorithm. To complete the formulation, the shape projections should be carefully defined to model different actuations in the simulation and to model the material properties geometrically. In the state-of-the-art work [9], the geometric constraints of actuations are modeled as a type of element, e.g., aligning the cable with the edge of elements and shorten the edges, or scaling the size of elements for volume expansion in pneumatic actuations. In such way, the actuation can be directly integrated in the optimization without additional computation burdens. In terms of modeling the material properties geometrically in the framework, a calibration step is done to learn the relationship between material properties and shape parameters between hard and soft assignments. Should the element be rigid or preserve its volume is determined by the shape parameters and modeled by the shape projection. It is shown that the calibration method can be used to simulate the deformation of objects with two materials. Different from using constrained nonlinear optimization, the geometry optimization can converge in a few iterations, thanks to the shape projection operator.
Discussion
The development of geometric simulation was motivated by the observation that most actuations of soft robots such as length shortening of cable and volume changing of chamber are based on geometry variation. The geometric optimization tries to preserve shape during deformation with the function of representing actuations as different type of geometric constraints to be imposed on specially designed elements. It shows promising results in terms of accuracy and efficiency, and it is also shown to be possible in the dynamic models [10].
Conclusion
The preliminary results of the geometry-based framework are attractive, and its efficiency opens the opportunity of iterative design for soft robot. However, the current development is still limited with simple structures, materials, and actuations. Therefore, to make this simulation more practical and user friendly, the future works should include extending to different actuations such as thermo, magnetism or electro ones; multiple actuations acting together; multiple materials; non-linear material like hyperplastic material [11]; and multiple bodies with collision detections.
References
- Gul JZ, Sajid M, Rehman MM, Siddiqui GU, Shah I, et al (2018) 3D printing for soft robotics–a review. Science and Technology of Advanced Materials 19(1): 243-262.
- Leung SY, Kwok TH, Li X, Yang Y, Wang CCL, et al. (2018) Challenges and Status on Design and Computation for Emerging Additive Manufacturing Technologies. J Comput Inf Sci Eng in press: 10.1115/1.4041913.
- Drotman D, Jadhav S, Karimi M, Zonia P, Tolley MT (2017) 3D printed soft actuators for a legged robot capable of navigating unstructured terrain. in IEEE International Conference on Robotics and Automation (ICRA), Singapore.
- Faure F, Duriez C, Delingette H, Allard J, Gilles B, et al. (2012) SOFA: A Multi-Model Framework for Interactive Physical Simulation. Soft Tissue Biomechanical Modeling for Computer Assisted Surgery, Berlin, Heidelberg, Springer, pp. 283-321.
- Duriez C, Coevoet E, Largilliere F, Morales-Bieze T, Zhang Z, et al. (2016) Framework for online simulation of soft robots with optimizationbased inverse model. IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots, San Francisco, CA.
- Bouaziz S, Deuss M, Schwartzburg Y, Weise T, PaulyM (2012) Shape- Up: Shaping Discrete Geometry with Projections. Comput Graph Forum 31(5): 1657-1667.
- Kwok TH, Chen Y (2017) Geometry-Driven Finite Element for Four- Dimensional Printing. ASME Journal of Manufacturing Science and Engineering 139(11): 10.1115/MSEC2017-2621.
- Peng Y, Deng B, Zhang J, Geng F, Qin W, et al. (2018) Anderson acceleration for geometry optimization and physics simulation. ACM Trans. Graph 37(4): 1-14.
- Fang G, Matte CD, Kwok TH, Wang CCL (2018) Geometry-based Direct Simulation for Multi-Material Soft Robots. IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia.
- Bouaziz S, Martin S, Liu T, Kavan L Pauly M (2014) Projective dynamics: fusing constraint projections for fast simulation. ACM Transactions on Graphics TOG 33(4): 1-11.
- Liu T, Bouaziz S, Kavan L (2017) Quasi-Newton Methods for Real-Time Simulation of Hyperelastic Materials. ACM Trans Graph 36(3): 1-16.






























