Design of Piezoceramic Length for Cantilever-Type Piezoelectric Generators
Guoce ZHANG*
Hainan University, China
Submission: December 04, 2018; Published: December 11, 2018
*Corresponding author: Guoce ZHANG, Hainan University, China.
How to cite this article: Guoce ZHANG. Design of Piezoceramic Length for Cantilever-Type Piezoelectric Generators. Robot Autom Eng J. 2018; 4(1): 555629. DOI: 10.19080/RAEJ.2018.04.555629
Abstract
A cantilever-type piezoelectric generator is analyzed under a harmonic excitation. The nonlinearity originates from the magnetic action at the free end of the cantilever. The electromechanical system is modeled as an integro-partial differential equation with nonlinear boundary conditions, a more reasonable model than those discrete models. Based on the distributed-parameter model, the length of the piezoelectric patch is designed. The electrical results are illustrated in detail for the first two vibration modes. It is revealed that the output performance can be improved for the automatically power generator with the designed results.
Keywords: Automatically power generator; Piezoelectric cantilever; Nonlinear vibration; Nonlinear boundary conditions.
Introduction
The power harvesting from ambient vibrations can be stored to support wireless sensors which are applied for temperature and humidity measurement and machinery acceleration monitoring. Such vibration-based generators can automatically transform mechanical energy into electrical energy to supply the maintenance-free, wireless electronics. The piezoelectric effect is an effective method of electromechanical transduction. Cantilever-type piezoelectric generators with piezoelectric patches have recently received increasing attention over the past two decades [1].
In order to capture more energy, nonlinear piezoelectric generators were proposed [2]. A cantilever subjected to nonlinear magnetic interactions is one of the mainly applied structures. Challa et al. [3] designed a power generator with tip magnets and experimentally measured the resonant frequency varying versus the transverse magnetic force. Cottone et al. [4] first proposed a bi-stable generator with magnetic nonlinearity, which can be changed into a mono-stable generator when the longitudinal magnetic force is small enough at the free end. These experimental results showed that magnetic nonlinearity could be utilized for exploiting vibratory energy widely available in many man-made systems. All the theoretical analyses in these nonlinear models above are based on a discrete model including the electromechanical coupling. Such oversimplified models will inevitably yield an error. Consequently, there should be a more reasonable distributed-parameter model for analyses.
As far as the author knows, there are only a limited number of investigations on the basis of distributed-parameter models. Stanton et al. [5] used the method of modal expansion into the governing equation, numerically computed a set of ordinary differential equations and discussed the periodic and chaotic characters of a bi-stable generator. By applying the three-mode expansion to the beam displacement, Wichenheiser & Garcia [6] numerically illustrated the transfer function of the normalized power based on a nonlinear model where the tip magnet was attracted by a stationary ferromagnetic structure. The improvement in the range of low frequencies enables the system to harvest energy effectively from a broadband, stochastic excitation. An optimization procedure is applied to human walking and automobile driving motions [7]. Abdelkefi [8]; Barsallo [9], Kim et al. [10] successfully employed one-term Galerkin truncation into the governing equation, an integro-partial differential equation. To the author’ knowledge, there have been no analytical results directly from the nonlinear distributed-parameter model without any truncation. The recent effort has been made on the analytical solution to the steady-state response of a cantilever-type piezoelectric generator.
The length of the piezoelectric patch is an important parameter to improve the generator’s performance. Different from a discrete model, the analytical result from the more reasonable continuous model can be devoted to theoretically design the piezoceramic length for all the vibration modes. Erturk et al. [11,12] was first interested in this problem. Considering the mass of piezoelectric layers, Abdelkefi et al. [13] investigated the effects of the piezoceramic length on both the natural frequency and the generated power. However, their experimental results are not comprehensive enough. In addition, their models are linear, without magnetic interactions. Based on the analytical results without any truncation, the author will also develop the conclusion on the design of the piezoceramic length from a linear model to a nonlinear model. The rest is organized as follows. The governing equations of the absolute and the relative motion of a cantilever-type piezoelectric generator are respectively shown. Subsequently, the length of the piezoceramic layer will be designed to improve the output power for each vibration mode. Finally, this paper ends with summary remarks.
Equations of absolute motion
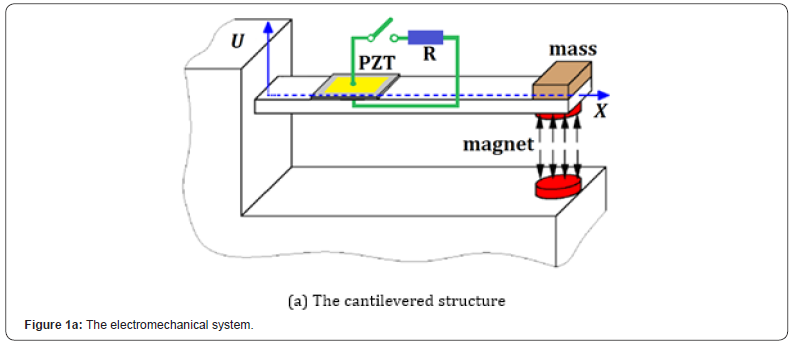
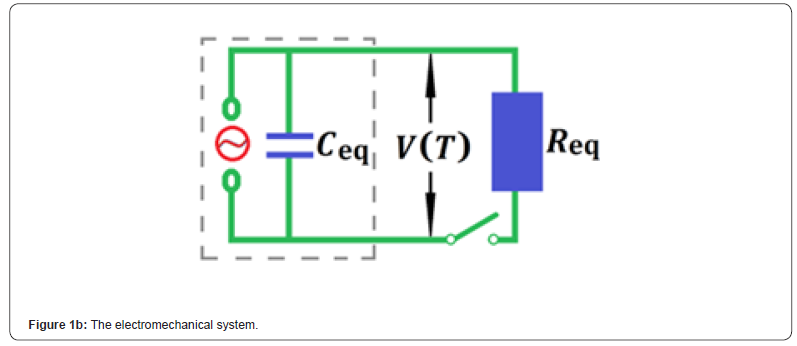
Cantilevered piezoelectric generators recently received a great deal of attention. As is shown in Figure 1, the considered electromechanical system is composed of a cantilevered structure (Figure 1a) with an electric circuit (Figure 1b). The cantilever, clamped at a framework, is assumed to be a slender and uniform beam with a rectangular cross section. The tip proof mass is used to adjust the fundamental natural frequency to the working frequency. A cylindrical permanent magnet is fixed at the free end of the cantilever beam. The magnet, modeled as a portion of the tip lumped mass, is perpendicularly repelled by a same cylindrical magnet which is attached to the framework. An extremely thin piezoelectric ceramic patch partially covers the surface of the cantilever. Two electrodes cover the opposite transversal faces of the piezoelectric ceramic layer. The two electrodes will be connected to a resistive load to generate electrical energy. As is illustrated in Figure 1b, the circuitry includes a resistive load as well as an internal capacitance because the electrode pair brackets the piezoceramic layer. According to Kirchhoff laws, the circuit equation can be expressed as
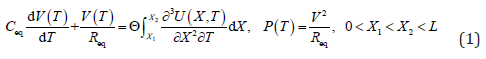
where the piezoelectric generator offers the current source, Ceq represents the equivalent capacitance, Req represents the equivalent resistance, Θ represents the electromechanical coupling coefficient, V(T) represents the voltage across the resistive load at the time of T, P(T) represents the power output, U(X, T) represents the transversal displacement of the cantilever whose clamped end is the original point, and X1 (or X2) represents the location of the most left (or right) end of the piezoelectric ceramic patch.
The applied cantilever beam is assumed to be made of Kelvin- Voigt visco-elastic material of viscosity coefficient Λ. A tip proof of mass mt (together with the tip magnet) is attached to the cantilever of mass mb, length L, Young’s modulus E, and area moment of inertial I. Since the electrode layer has an influence on the bending stiffness, the internal bending moment of the cantilever can be represented as
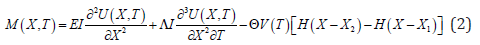
where the effect of the thin piezoelectric patch is supposed to be negligible. In Eq. (2), H denotes the unit step function (also known as Heaviside function), which is defined as the integral of the Dirac delta function. If 0 < X < L, the equation of motion is
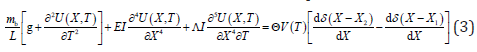
where g is the acceleration of gravity, and the Dirac delta function satisfies

The two applied cylindrical magnets are both with height Hm and radius Rm. The initial distance between them is symbolically denoted by Dm while the entire structure is just equipped. ρm is the residual magnetic flux density. Sm is the common area between the two magnets. μair is the permeability of air. The distance between the two magnets plays indispensable roles in generating nonlinear magnetic force. The repulsive force between the two cylindrical magnets was formulated in the form of
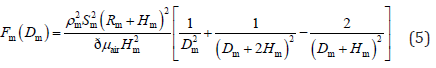
where π is the ratio of circumference to diameter.
The following is the boundary conditions at X = 0 or L. For a slender cantilever, the small tip magnet can be modeled as a point mass, and the magnetic force serves the nonlinear boundary condition at the right end of the cantilever. At its left end, the transversal position of the excited base is assumed to be Bsin(ΩT). Then the associated boundary conditions are given by
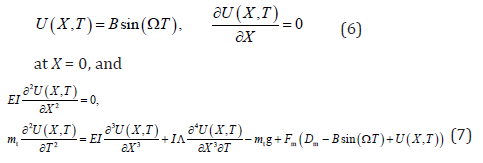
at X = L. Eq. (7) gives the nonlinear boundary condition, which is dependent on time. It should be noted that the magnet at the base is also moving harmonically and serving the nonlinear boundary conditions. We make this assumption so that the entire generator works at a practical vibrating source (rail, road, or bridge), not in a laboratory.
Introduce dimensionless parameters as follows.

where e is the unit voltage (1 volt). From Eqs. (1), (3) and (8), the previous application of the Euler-Bernoulli beam theory yields the dimensionless governing equation, which is represented algebraically as
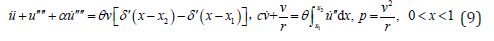
where the superscript prime represents the (partial) derivative of the preceding function taken with respect to its spatial variable x, and the overdot denotes the (partial) derivative over the time variable t. The corresponding boundary conditions are simplified as
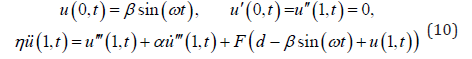
where the non-dimensional magnetic force function is
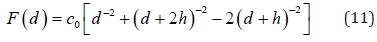
Equations of relative motion
In the following, we will determine the equilibrium equation that is irrelative with time and establish the standard governing equation of motion around the equilibrium.
From Eqs. (9) and (10), the equilibrium position 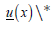 MERGEFORMAT satisfies
MERGEFORMAT satisfies
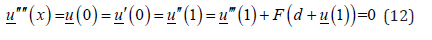
The solution to Eq. (12) is in the form of

where Ae satisfies
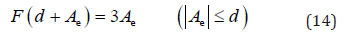
Introduce a new coordinate transformation.
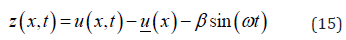
Substituting Eq. (15) into Eq. (9) yields the standard governing equation of relative motion.
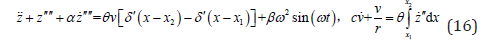
Substituting Eq. (15) into Eq. (10) yields the corresponding boundary conditions.
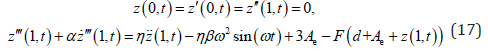
Taylor series expansion method can be applied to deal with the nonlinear terms in the boundary condition (17). If the displacement is small,
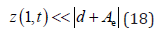
the following series expansion is valid

where j = 1,2,3,…
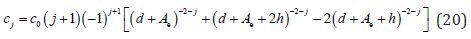
Solutions to Governing Equations
In the absence of all nonlinear terms and external excitation, the natural frequencies have been computed from the following equation [14].
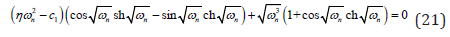
The nth modal function with the condition 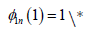 MERGEFORMAT satisfies
MERGEFORMAT satisfies
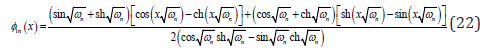
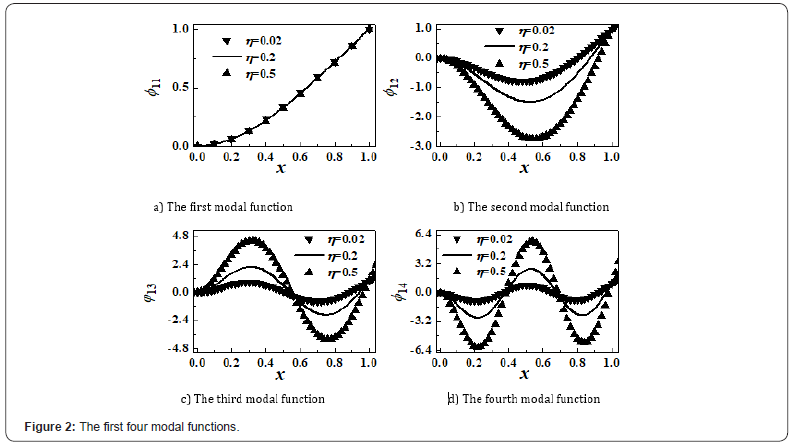
Figure 2 shows the first four modal functions. The considered parameters are L=0.48m, mb=2.56×10–2kg, mt=5.12×10–4kg, g=9.8067m/s2, E=3.81×1010Pa, I=3.6×10–13m4, Hm=0.002m, Rm=0.004m, ρm=1.1Tesla, Dm=0.3385m, Sm=5.0265×10–5m2 and μair=1.256×10–6H·m–1 [3]. The dimensionless values are c0=0.5084, d=0.15, h=0.004167, and η=0.02. The effect of tip mass on modal functions are illustrated in Figure 2 with η = 0.02, 0.2 and 0.5. It can be found from these figures that there are different numbers of points of inflection for different vibration modes.
Then the nonlinear steady-state response can be expressed in the form of [14]
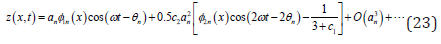
where θn stands for the phase angle, the new functions with respect to x are
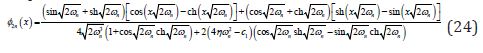
and an represents the amplitude of the first-order approximation to the steady-state motion, satisfying

where

The output voltage is approximately
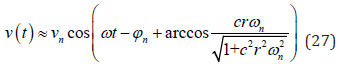
where

Then vn represents the approximate amplitude of the simple harmonic voltage of the steady-state response. Consequently, the average value of the power output approximately satisfies
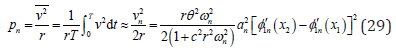
Results and Discussion
When the electrical load is specified, and the magnetic parameters are well defined, the piezoceramic length is an interesting parameter. According to Eq. (25), the response amplitude satisfies
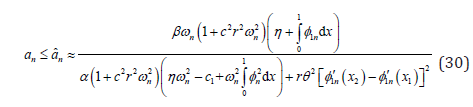
From Eq. (28) through (30), for different excitation frequencies,

and

The length of piezoceramic layer is designed according to the peak average (32) of power output. The maximum of peak average of power output is pursued. Now we regard the peak values (30) through (32) as three functions of x1 and x2. If the difference of the slopes of the modal function at two ends of the electrodes is zero, the maximal peak of the response amplitude (30) occurs. At the same time, it can be found from Eqs. (31) and (32) that the electrical response is continuously zero due to the charge cancellation. In the opposite position, the maximal peak of output voltage or power occurs when the difference of the slopes of modal function at two boundaries of the electrode pair approximately satisfies

At the clamped end, the slope of the modal function is always zero at the original point. Let x1 = 0 in general. Then there would be a superior performance to generate electrical energy if the electrode pair covers (0, x2) where the right boundary of the electrode pair satisfies
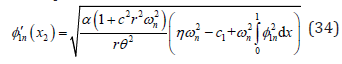
The considered dimensionless parameters are α = 0.0005, β = 0.0001, c0 = 0.5084, d = 0.15, h = 0.004 167, η = 0.02, c = κ = 0.000 001 and θ = 0.0002 [14]. In the first resonance region, the electromechanical coupling coefficient is large enough, and the solution to Eq. (34) is x2 = 0.2839. Then the comparison between two piezoelectric intervals (0, 0.2839) and (0,1) is made on the frequency-voltage and frequency-power curves in Figure 3. The solid lines represent the designed results. The dashed lines represent those results when the piezoelectric patch is covering the entire cantilever. It can be observed that the curves with a designed piezoceramic layer will have a larger peak of the average value of power output or the amplitude of the output voltage. Then the designed piezoelectric generator will have a larger electrical output from the high-energy attractors in a small range of frequency. On the contrary, it is necessary to avoid the lowenergy attractors.


At present, the problem on the length of the piezoelectric layer seems to be solved. Unfortunately, there is no solution to Eq. (34) in the interval (0, 1] for the second mode. As a matter of fact, there will always be no solution to Eq. (33) for a small electromechanical coupling coefficient. Then the produced electrical energy strongly depends on the difference of the slopes (34). If the difference (34) at two boundaries of the electrode pair is zero, the output voltage or power vanishes according to Eqs. (31) and (32). The physical reason is the existence of the strain nodes where the curvature eigenfunction of each mode shape of the cantilever changes sign. The strain nodes of each vibration mode are defined as the points of inflection of the respective modal function. For diverse ratios of the tip mass to the mass of the cantilever beam, Figure 4 illustrates the position of strain node of the first two mode shapes where
In Figure 4, the solid lines, the dotted lines, the dot-dashed lines and the dashed lines respectively represent the ratio 0.02, 0.2, 0.5 and 1.0. As is known to all, if the initial distance d between two magnets is very large, the magnetic nonlinearity will be ignorable. It can be remarked from Figure 4a that there is no strain node in the open interval (0,1) at the fundamental mode of a linear cantilevered piezoelectric generator. Then the strain distribution along the length of the cantilever is in phase in the first mode shape. The electrodes may cover the entire cantilever in the test of the fundamental mode. This conclusion completely coincides with that obtained experimentally by Erturk et al. [12]. Compared with a linear piezoelectric generator, an extra strain node might exist for a nonlinear cantilevered piezoelectric generator with a small ratio of the tip mass to the beam mass. The newly-born strain node is useful when the electromechanical coupling coefficient is small enough. Then it might be optimal that the piezoceramic layer covers the interval (0, s1) or (s1, 1), while the continuous electrodes covering the entire cantilever will inevitably lead to a charge cancellation. From Figure 4b, there is only one strain node in the open interval (0, 1) for the second mode. However, there will be at least two nodes for higher-order modes. Then it might be optimal if the piezoelectric patch is placed between two nodes.
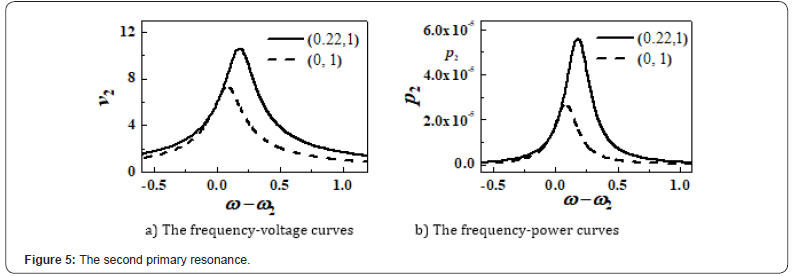
As is stated previously, to avoid the cancellation of the electrical output of the cantilevered piezoelectric generator with weak electromechanical coupling, the piezoceramic layer should be placed between two adjacent strain nodes. Then the optimal design for the second mode will be the region (s2, 1) because one is also a strain node. The strain node s2 is equal to 0.2200 if the considered dimensionless parameters are same with Figure 3. Figure 5 illustrates the comparison between two piezoelectric intervals (0.22,1) and (0,1) at the second primary resonance. It can be concluded that the optimized piezoelectric generator will have a wider band of frequency as well as a larger electrical output.
After all, the optimal length of the piezoceramic layer is different for different primary resonances. When the electromechanical coupling coefficient exceeds the respective critical value (changing with different resonances), the effect of the coupling terms on the response amplitude should be taken into consideration. The difference of the slopes of the modal function at two boundaries of the electrode pair should satisfy (33). For a nonlinear piezoelectric generator, the electrical output from the high-energy attractors might be optimal. For quite a small coupling coefficient, there will be no solution to (33) in the interval [0,1]. Then the larger the absolute value of the difference of the two slopes, the better the output performance. The maximal value might occur in the interval between two strain nodes, or between one strain node and one end of the cantilever. All these designed results are on the length of a single piezoceramic patch and an electrode pair. Using more finely segmented electrode pairs will result in a larger electrical output [15]. In particular, the application of segmented electrode pairs will yield much more electrical output for a cantilever-type piezoelectric generator with strong electromechanical coupling.
Conclusion
The present work investigates a cantilevered piezoelectric generator with nonlinear magnetic boundary conditions. An approximate solution to the governing equation is pursued without any truncation. The length of the piezoelectric layer is designed directly from the integro-partial differential equation. The problem is associated with the strain nodes of each vibration mode. In the fundamental mode, there is no strain node between both ends of a linear piezoelectric cantilever, while an extra node might exist in the nonlinear generator. Then the continuous electrodes covering the entire cantilever will lead to a charge cancellation.
To avoid the charge cancellation, the electromechanical coupling coefficient plays a key role on the design of the optimal piezoceramic length. For a cantilevered piezoelectric generator with weak electromechanical coupling, the devised length strongly depends on the bending strain distribution. The electrodes should be located between two adjacent strain nodes, or between one node and one end of the cantilever. When the coupling coefficient exceeds a critical value, the electrical output might be optimal if there is a right difference of the slopes of the modal function at two boundaries of the electrode pair.
Acknowledgement
The work was supported by Hainan Provincial Natural Science Foundation (No. 118QN183), the National Natural Science Foundation of China (Nos. 11502135 and 11602131), the Scientific Research Foundation of Hainan University (Nos. KYQD(ZR)1712 and hdkytg201708) and China Postdoctoral Science Foundation (No. 2016M591648).
References
- Wei CF, Jing XJ (2017) A comprehensive review on vibration energy harvesting: modeling and realization. Renewable and Sustainable Energy Reviews 74: 1-18.
- Daqaq MF, Masana R, Erturk A, Quinn DD (2014) On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion. Applied Mechanics Review 66: 040801.
- Challa VR, Prasad MG, Shi Y, Fisher FT (2008) A vibration energy harvesting device with bidirectional resonance frequency tenability. Smart Materials and Structures 17: 015035.
- Cottone F, Vocca H, Gammaitoni L (2009) Nonlinear energy harvesting. Physical Review Letters 102: 080601.
- Stanton SC, McGehee CC, Mann BP (2010) Nonlinear dynamics for broadband energy harvesting: investigation of a bistable piezoelectric inertial generator. Physica D 239: 640-653.
- Wichenheiser AM, Garcia E (2010) Broadband vibration-based energy harvesting improvement through frequency up-conversion by magnetic excitation. Smart Materials and Structures 19: 065020.
- Wichenheiser AM (2011) Design optimization of linear and non-linear cantilevered energy harvesters for broadband vibrations. Journal of Intelligent Material Systems and Structures 22: 1213-1225.
- Abdelkefi A, Barsallo N (2014) Comparative modeling of low-frequency piezo magnetoelastic energy harvesters. Journal of Intelligent Material Systems and Structures 25: 1771-1785.
- Abdelkefi A, Barsallo N (2016) Nonlinear analysis and power improvement of broadband low-frequency piezomagnetoelastic energy harvesters. Nonlinear Dynamics 83: 41-56.
- Kim P, Yoon YJ, Seok J (2016) Nonlinear dynamic analyses on a magnetic piezo elastic energy harvester with reversible hysteresis. Nonlinear Dynamics 83: 1823-1854.
- Erturk A, Inman DJ (2008) A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. ASME Journal of Vibration and Acoustics 130: 041002.
- Erturk A, Tarazaga PA, Farmer JR, Inman DJ (2009) Effect of strain nodes and electrode configuration on piezoelectric energy harvesting from cantilevered beams. ASME Journal of Vibration and Acoustics 131: 011010.
- Abdelkefi A, Barsallo N, Tang LH, Yang YW, Hajj MR (2014) Modeling, validation, and performance of low-frequency piezoelectric energy harvesters. Journal of Intelligent Material Systems and Structures 25: 1429-1444.
- Zhang GC, Chen LQ, Ding H (2014) Forced vibration of tip-massed cantilever with nonlinear magnetic interactions. International Journal of Applied Mechanics 6: 1450015.
- Wang HY, Tang LH, Shan XB, Xie T, Yang YW (2014) Modeling and performance evaluation of a piezoelectric energy harvester with segmented electrodes. Smart Structures and Systems 14: 247-266.






























