Numerical Study on Low Velocity Impact Response of Functionally Graded Carbon Nanotube Reinforced Composite Beams
Mohsen Kashfi1, Mohammad Kashfi2* and Mostafa Sabzikar Boroujerdy3
1Department of Engineering, Varamin-Pishva Branch, Islamic Azad University, Iran
2Faculty of Engineering, Ayatollah Boroujerdi University, Iran
3 Department of Engineering, Firoozkooh Branch, Islamic Azad University, Iran
Submission: October 14, 2018; Published: November 15, 2018
*Corresponding author: Mohsen Kashfi, Department of Engineering, Varamin-Pishva Branch, Islamic Azad University, Iran
How to cite this article: Mohsen K, Mohammad K, Mostafa S B. Numerical Study on Low Velocity Impact Response of Functionally Graded Carbon Nanotube Reinforced Composite Beams. Robot Autom Eng J. 2018; 4(1): 555626. DOI: 10.19080/RAEJ.2018.04.555626
Abstract
In this work response of functionally graded carbon nanotube reinforced composite beam subjected to the action of an impacting mass is investigated analytically and numerically. Timoshenko beam theory is used to estimate the kinematics of the beam. Material properties of the composite are obtained using a refined rule of mixture. However, for numerical model surface to surface has been used. The beam cross section considered uniform and the impactor assume a Steel made ball. Numerical has reasonable agreement compare with analytical model and results show that the Fem model can predict the beam behavior with very good agreement.
Keywords: Carbon nanotube; Timoshenko beam; Finite element method; Low velocity impact
Introduction
Carbon nanotubes (CNTs) are known as a novel class of materials which have attracted increasing attention in recent years. These materials have exceptional mechanical properties which make them as a potential candidate for the reinforcement of the composites [1]. Distribution of CNTs in a polymeric matrix may be uniform or functionally graded (FG). Lin and Xiang analyzed the linear [2] and nonlinear [3] free vibration characteristics of first order and third order shear deformable FG-CNTRC beams. In the present work the response of FG-CNTRC beams under low velocity impact based on the first order Timoshenko beam theory and FE modeling investigated.
Governing Equations
Consider an FG-CNTRC beam of thickness h, width b, and length L referred to the conventional coordinates system (),,xyz where as usual 0 ≤ x ≤ L is through the length, -h/2 ≤ z ≤ +h/2 is through the thickness and -b/2 ≤ y ≤ +b/2 is through the width. Due to simplicity in the present study the rule of mixtures is used by introducing CNT efficiency parameters and the material properties of CNTRC beam. Thus, the material properties can be written as [4]:
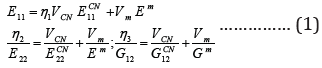
where ECN11, ECN22 and GCN12are the Young’s modulus and shear modulus of SWCNTs, respectively. Besides, Em and Gm indicate the corresponding properties of the isotropic matrix. The coefficients η1, η2 and η3 are introduced to account for the scale dependent material properties. These constants are evaluated by matching the effective properties of CNTRC obtained from the molecular dynamic simulations with those from the rule of mixtures [4]. Furthermore, in Eq. (1), VCN and Vm are the volume fractions of CNTs and matrix phase, respectively, which satisfy the condition VCN+Vm=1
Referring to the basic relations of strains and displacements, on a generic point of the beam, equation for the strain components can be written as belo
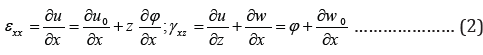
And the constitutive equations of the beam when only axial and transverse components of stress field are present can be formulated as
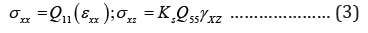
In the Eq. 3, Ks is the shear correction factor and is taken as Ks= π2/12[5]. Besides, 11Q and 55Q are evaluated in terms of the material constants as Eq. (4)
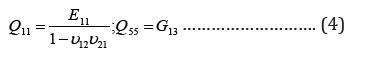
Where , Nx, Mx and Qx are the normal force, bending moment and shear force resultants that are defined by
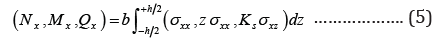
Finite Element Simulation
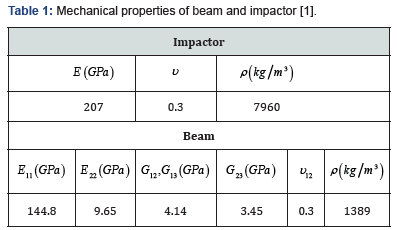
The numerical simulations were performed using the commercial finite element code, MSC MARC. The numerical model consisted of 5591 elements for beam and impactor. The model, dimensions and the boundary conditions are shown in Figure 1. At the beginning the horizontal position of impactor assumed 100mm from clamed support and the initial velocity considered 2m/s based on experimental result which are available in reference [6]. The mechanical properties of beam and impactor are presented in Table 1.
Result and discussion
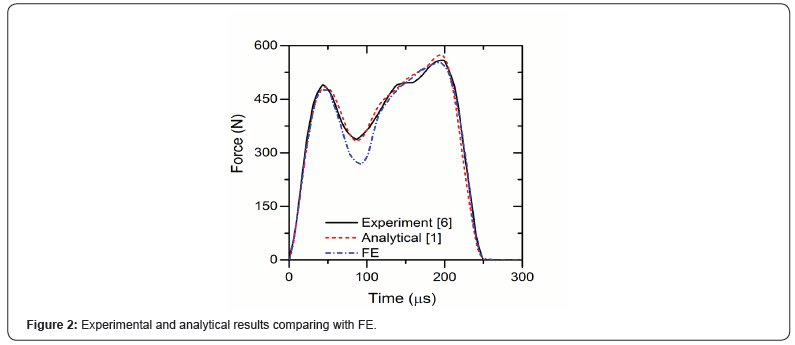
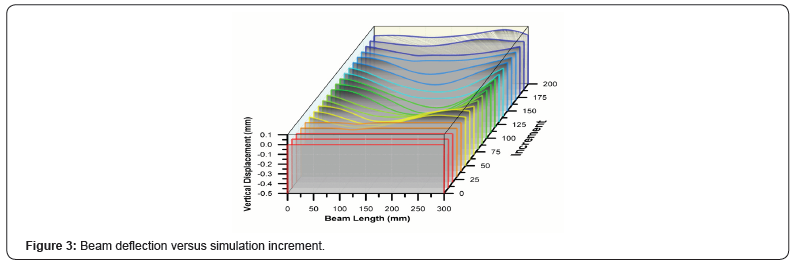
In order to validate the FE model results an experimental result is carried out in this section. Experimental and analytical results are extracted from previous works and reported here. Figure 2 shows the compression between FE, experimental and numerical results. It is observable that the numerical results have reasonable agreement with experiment and analytical solution. The curve has two peaks which are completely observable in mentioned figure. Numerical model predicted a lower value after first peak because in FE model the ball is not completely sphere shape thus the surface of it is not smooth enough thus the contact force decreased compare with experiment and analytical solutions after first contact force peak. Figure 3 illustrates the beam deflection versus time after ball impact. As expected, the deflection starts at impactor position at the beginning of impact then the stress waves move though the beam and make the defilation on the other position of it. The maximum and minimum of beam deflection are about -0.5 to 0.1mm.
Conclusion
The behavior of an FGM beam is investigated by a FE method under low velocity impact. The beam supports were considered clamped and simply support to verify the numerical simulation. The FE model can predict the beam behavior with reasonable agreement with experiment and analytical model. The deflection history of beam extracted and the deflection pattern of beam under low velocity impact obtained in each solution increment.
References
- Jam J, Kiani Y (2015) Low velocity impact response of functionally graded carbon nanotube reinforced composite beams in thermal environment. Composite Structures 132: 35-43.
- Lin F, Xiang Y (2014) Vibration of carbon nanotube reinforced composite beams based on the first and third order beam theories. Applied Mathematical Modelling 38(1516): 3741-3754.
- Lin F, Xiang Y (2014) Numerical Analysis on Nonlinear Free Vibration of Carbon Nanotube Reinforced Composite Beams. International Journal of Structural Stability and Dynamics14(01): 1350-1356.
- Hui-Shen HS (2011) Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part I: Axially-loaded shells. Composite Structures 93(8): 2096-2108.
- Ansari R, Faghih Shojaei M, Mohammadi V, Gholami R, Sadeghi F (2014) Nonlinear forced vibration analysis of functionally graded carbon nanotube-reinforced composite Timoshenko beams. Composite Structures 113: 316-327.
- Lam KY, Sathiyamoorthy TS (1999) Response of composite beam under low-velocity impact of multiple masses, Composite Structures 44(2): 205-220.






























