Stages and Technology of Surface Areas Studying of Cone’s Polyhedral Triangulations as a Means of School Student’s Developing at Creativity Thinking
Eugeny I Smirnov1*, Artiom D Uvarov2 and Sergey A Tikhomirov3
1Doctor of Sciences in Education, Professor, Head, Mathematical Analysis, Theory and Methods of Teaching Mathematics Department, Yaroslavl State Pedagogical University named after K. D. Ushinsky
Leading Scientific Researcher, Vladikavkaz Scientific Center of the Russian Academy of Sciences
Southern Mathematical Institute of the Russian Academy of Sciences, Russia
2Philosofy Doctor in Mathematics, Associate Professor, Mathematical Analysis, Theory and Methods of Teaching Mathematics Department, Yaroslavl State Pedagogical University named after K. D. Ushinsky, Russia
3Philosofy Doctor in Mathematics, Associate Professor, Geometry and Algebra Department, Yaroslavl State Pedagogical University named after K. D. Ushinsky, Russia
Submission: August 27, 2024; Published: September 05, 2024
*Corresponding author: Eugeny I Smirnov, Doctor of Sciences in Education, Professor, Head, Mathematical Analysis, Theory and Methods of Teaching Mathematics Department, Yaroslavl State Pedagogical University named after K. D. Ushinsky, Russia
How to cite this article: Eugeny I Smirnov*, Artiom D Uvarov and Sergey A Tikhomirov. Stages and Technology of Surface Areas Studying of Cone’s Polyhedral Triangulations as a Means of School Student’s Developing at Creativity Thinking. Psychol Behav Sci Int J. 2021; 22(2): 556084. DOI: 10.19080/PBSIJ.2024.22.556084.
Abstract
The development of complex mathematical concepts and procedures by school students in the course of search and research activities creates a precedent for identifying the essence of basic educational elements (surface area, fuzzy logic and fuzzy sets, iterative processes, Schwartz cylinder and cone, fractals, numerical and asymptotic methods, etc.). At the same time, factor impulses of self-organization of school students based on parameterization methods, founding of personal experience, cultures dialogue and identification of generalized rules and procedures of cognitive activity on the base of visual modeling. The objectives: to develop the creativity of school student’s thinking based on the development of complex systems and knowledge generalized constructs, to build a stages and technologies for organizing research activities based on the mathematical and computer modeling symbiosis with the manifestation of mathematical education synergy. The phenomenon of surface area concept of two-dimensional manifolds (cylinder and cone) reveals its essential connections based on the symbiosis of mathematical and computer modeling by means of experimental mathematics. The effectiveness of mathematical education management processes with a synergetic effect under conditions of uncertainty, variability and self-organization of cognitive processes during triangulation of two-dimensional manifolds polyhedral surfaces (Schwartz cylinder and Schwartz cone) is shown.
Keywords: Synergy; Schwartz Cylinder; Schwartz Cone; Mathematical Modeling; Computer Design
Introduction
Mastering of complex cognitive activity (generalized constructs of complex systems and knowledge) allows you to create for development conditions of school student’s creative thinking and are not a destructive element (taking into account its variability and accessibility for the individual) to achieve an educational goal. It is the pedagogical management of complex systems and knowledge development based on mathematical and computer modeling symbiosis that can give a powerful motivational charge to the study of mathematics, school student’s self-organization and personal qualities development (Morin E[11], Mainzer K[20], Haken H[7], Prigozhin I[9], etc.). The overcoming effect of complex mathematical knowledge analyzing in research creates the phenomenon of self-organization and manifestation of synergetic effects, obtaining by-products of research and creative thinking [5,8,9,17,18]. Problem: what are the stages and technology of an essence researching of complex systems and knowledge generalized constructs with school student’s self-organization effect and creativity development? The leading idea: manifestation of self-organization and creativity in teaching mathematics to complex systems and knowledge is possible on the basis of mathematical and computer modeling symbiosis, cultures dialogue and an identification of synergy attributes (attractors, bifurcation points, pools of attraction, iterative procedures, etc.) during the development of “problem areas” of mathematical education. Thus, the present study is an attempt to develop the stages and technologies for school student’s research activities organizing based on mathematical and computer modeling symbiosis of complex knowledge in the “problem areas” of mathematical education. This is accompanied by synergetic effects manifestation and the identification of new by-products of research based on school student’s selforganization and cognitive activity.
Methodology and Methods
The technology implementation is associated with school student’s complex systems and knowledge development by means of mathematical and computer modeling symbiosis in saturated information and educational environment [1]. An important factor is the statement of goal-setting multiplicity, building of stages and hierarchies of symbolic, experimental and figurative geometric activities in the direction of an essence founding of mathematical objects and procedures, cultures dialogue and school student’s network interaction [2]. The real manifestation of school student’s self-organization and creativity is complex systems and knowledge development (including modern achievements in science [3, 4], search and analysis of side solutions using information technology, an identification of bifurcation transitions, attractors of iterative procedures and pools of attraction in real processes based on variability, digitalization and parameterization, an ensuring coherence of information flows in the emergence of new dial-based product on cultures dialogue manifestation [5,6]. This methodology corresponds to the concept of post-non-classical scientific picture of the world as a self-organization paradigm of nonlinear systems dynamic Haken G [7], Kuhn T, Knyazeva EN, Mandelbrot B [8], Prigozhin IR [9], Kurdyumov SP, Mainzer K [20], etc. in cognition of complex knowledge itself process “becomes a communication, a loop between cognition (phenomenon, object) and the cognition of cognition” Morin E [11].
The content of school students’ research activity stages is determined by the content of founding modes of complex systems and knowledge mastering:
I. Procedural Modes (the principle and technology of personal experience founding Husserl E, Heidegger M, Shadrikov VD, Smirnov EI [12-13], etc.; creation of a motivational field for the study of complex mathematical constructs (including the disclosure of samples and standards depository for complex systems and knowledge studying); building hierarchies in the deployment of generalized construct essence of mathematical education “problem zone”; visual modeling, parameterization and an abstraction and functionality stages for study of complex knowledge generalized constructs; search for bifurcation points and an attraction pools of knowledge constructs by means of iterative processes constructing based on mathematical and computer modeling.
II. Meaningful Modes (an actualization of factor impulses for the formation of school student’s research behavior in mastering process of complex mathematical knowledge): development and implementation in the educational process of standards and samples of scientific search for practiceoriented complex problems in mathematics education “problem zones”, based, among other things, on modern achievements in science (fractal geometry, an encoding theory and encryption of information, Schwartz cylinder, cellular automata, fuzzy sets and fuzzy logic, etc.); formulation and multiple goal setting of multi-stage mathematical and information tasks content Klyaklya M, Sekovanov VS [14], Smirnov EI [15], etc., manifestation of mathematical education synergy in the context of an identifying by-products studying of basic problem: fractal objects, information and mathematical models, computer modeling, stochastic structures, etc. Sekovanov VS, Poddyakov AN [10], Dvoryatkina SN [16], Uvarov AD [17].
III. Personal Adaptation Modes (group interaction of school students and self–organization of personality; founding procedures for transition from present state of creativity to its generalized potential development; an expression of characteristics and qualities of personal development and school student’s adaptation in the process of complex mathematical knowledge mastering in self-actualization direction (“I’m interested in this”), self-determination (“what can I do”), self-organization (“I am able to manage the process”), selfdevelopment (“I can do something new”) [18]. At the same time, the variety of practice-oriented tasks and related to an essence studying of complex knowledge generalized constructs (surface area, function limit, arc length, set measure, etc.) allows for variability and consideration of each school student’s personal preferences. The synergy manifestation of complex knowledge based on mathematical and computer modeling symbiosis also contributes to the formation of mathematical and digital literacy and the growth of each school student’s creative potential.
Results
Synergetic Effects Studying of Polyhedral Surface Areas of Schwartz Cone
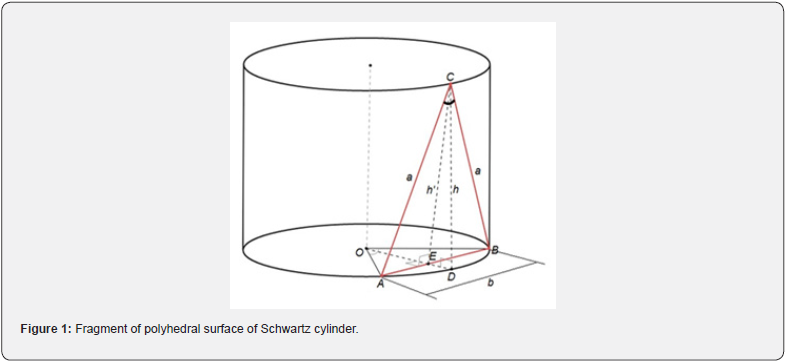
Example: The generalized construct of scientific knowledgethe concept of surface area, being a difficult object to understand, is indirectly actualized and manifests its essence through computer and mathematical modeling of studying processes of lateral surface “area” of Schwartz cylinder and cone [17], [19]. At the end of XIXth century, T. Schwartz showed that concept definition of surface area by triangulation and the corresponding areas of polyhedral surfaces leads to paradoxes (unlike the length of an arc on a plane). Therefore, the multiple goal-setting of an actualization processes of “surface area” concept by methods of an area studying of Schwartz cylinder (the content aspect) allows us to an identify the insignificant connections in the concept: pathological properties of the “area” of cylinder’s lateral surface are well studied in the so-called “regular” and “irregular” cases [17]. Namely, it is shown that the area of Schwarz cylinder’s polyhedral surface (based on triangulations of cylinder’s lateral surface) (Figure 1) is found by formulas (1)-(2), by means of the resulting polyhedral at m,n→∞ :
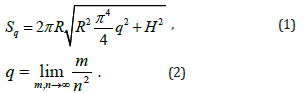
Thus, the “area” of lateral surface Sq of a regular Schwarz cylinder of height H and radius R (if this limit exists – finite or infinite) is completely determined by the limit (1) (Figure 1).
At the same time, due to the independent nature of an
aspiration m,n→∞ , the result of limiting process becomes
a poorly predictable, ambiguous, with an absence of patterns in
chaotic unfolding of fractal structures of polyhedral. Mandelbrot
B [8] showed that for m = nk the area of a polyhedral surface
grows as nk ( k ≠ 2 ). A similar pattern is observed in the study
of “irregular” Schwartz cylinders, when the height of cylinder is
divided into uneven layers (maximum height of the layers is an
infinitesimal value) [5, 15]. Hierarchies of issues arise (related to
the study of triangulations and polyhedral surfaces of Schwartz
cone) are solved by means of computer and mathematical
modeling on school student’s research activities in small groups in
a remote environment or in the form of multi-stage mathematical
and informational tasks studying. Such studies conducted by
school students in resource or laboratory calculation classes
(when multi-stage mathematical and information tasks solving)
during the research activities or networking develop the creativity,
an intellectual thinking operation, an increase of educational
motivation and the quality of mathematical activities mastering.
Consider a cone of height H and radius R. Let’s split the height H
into m equal parts. Through the obtained points we will draw m
parallel planes to the plane of cone base. Each plane intersects the
cone in a circle. We will distribute the n points evenly on these
circles. At the same time, each regular n-gon in the layer is rotated
by relative to the n-gon of previous layer by an angle  . The
layers are counted from the top of cone. Triangulate the resulting
set of points on the cone in the same way as the triangulation of
points set for Schwartz cylinder was carried out. As a result of the
manipulations performed, we obtain a certain surface – Schwartz
cone (Figure 2).
. The
layers are counted from the top of cone. Triangulate the resulting
set of points on the cone in the same way as the triangulation of
points set for Schwartz cylinder was carried out. As a result of the
manipulations performed, we obtain a certain surface – Schwartz
cone (Figure 2).
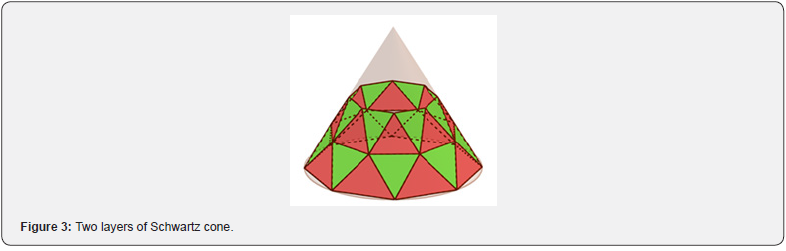
We derive the formula for an area of lateral surface of Schwartz cone. For certainty, we will consider a cone with a height H = R = 1. Let’s take a closer look at two layers of the cone (Figure 3).
As can be seen from the figure, each layer of Schwartz cone consists of two types of an isosceles triangles. In this case, the isosceles triangles of first type lie on the upper boundaries of layers, and the vertices of triangles of second type lie on the lower boundaries of layers. It is easy to understand that triangles of different types have the different areas even within the same layer. And it is quite obvious that their areas vary from layer to layer. Let’s calculate the areas for triangles of each type in one layer. To do this, consider the following Figure 4.



First, let’s calculate the area of a triangle of second
type: 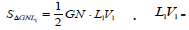 height, drawn to base of the
triangle
height, drawn to base of the
triangle 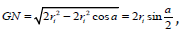 where
where 
 and
and 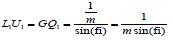 . Note, that.
. Note, that.  Finally, we have:
Finally, we have:

Similarly, you can calculate the area of a triangle of first type. Exactly:
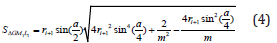
The area of layer with an index is equal to 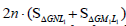 . Finally, the area of lateral surface of Schwartz cone is calculated
using the formula:
. Finally, the area of lateral surface of Schwartz cone is calculated
using the formula:

It should be noted that in the case when R = H = 1 , radius
 .
.
Formula (5) is presented as a sum and it is very difficult to understand from its dependence of an area of lateral surface of Schwartz cone on the limit (1). However, it is possible to estimate the area S using the limit (1). Consider the meridians on Schwartz cone. They are obtained by dissecting the cone with planes passing through the axis of cone and the vertices of regular 2n-gon lying at the base of cone. At the same time, the number of faces on two adjacent meridians differs by one. Each meridian passes through the faces of two types described above. Let’s sum up an area of faces of first and second types along the meridian.
Let be  is an area of first type face lying in a layer with a
number and on a meridian with an even index . Accordingly,
is an area of first type face lying in a layer with a
number and on a meridian with an even index . Accordingly, 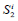 - is
an area of second type face lying in a layer with a number i +1
and on a meridian with an even index 2k ( 0 ≤ k < n ). It follows
from formula (3) that
- is
an area of second type face lying in a layer with a number i +1
and on a meridian with an even index 2k ( 0 ≤ k < n ). It follows
from formula (3) that

Similarly, it follows from formula (4) that
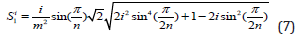
It’s easy to see that  . For the
sake of certainty, let’s assume that the number of layers is an even
number. Then, taking into account the last inequality, we get:
. For the
sake of certainty, let’s assume that the number of layers is an even
number. Then, taking into account the last inequality, we get:
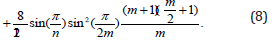
If in inequality (8) we go to the limit in m and n , then it will take the form:

A similar inequality can be obtained for the limit of an areas
sum for the faces of first type. Indeed, it follows from formula (7)
that 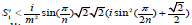 and, accordingly, there is
inequality:
and, accordingly, there is
inequality:

Since the total number of meridians is equal 2n , the number of meridians with even indices is equal . Hence, taking into account inequalities (9) and (10), we obtain:
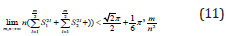
Thus, the limit of an areas sums for all faces lying on meridians with even indices for m,n→∞ is determined by inequality (11) and thus depends on limit (1). It should be noted that in this case inequality (8) does not take into account the area of last face lying on the meridian with an even index. However, the limit (9) remains true, since the area of each face tends to zero. If we carry out similar reasoning to estimate the areas of faces lying on meridians with odd indices 2k +1( 0 ≤ k < n −1), then in inequality (8) the index 2l must be changed to an index 2l −1, as a result of which inequality (8) will remain the same (assuming is an even number). Taking into account the latter reasoning, we obtain an estimate for an area of Schwartz cone’s lateral surface

The following Figure 5 demonstrates the behavior of Schwartz cone’s surface area with height H = 1 and radius R = 1 at m = n , while 200 ≤ n ≤ 800 :(Figure 5).
As prescribed by inequality (14) in the case when  the area of Schwarz cone tends to the area of lateral surface of an
ordinary cone with R = H = 1, that is to
the area of Schwarz cone tends to the area of lateral surface of an
ordinary cone with R = H = 1, that is to  . The following Figure
6 shows the behavior of Schwartz cone’s surface area with height
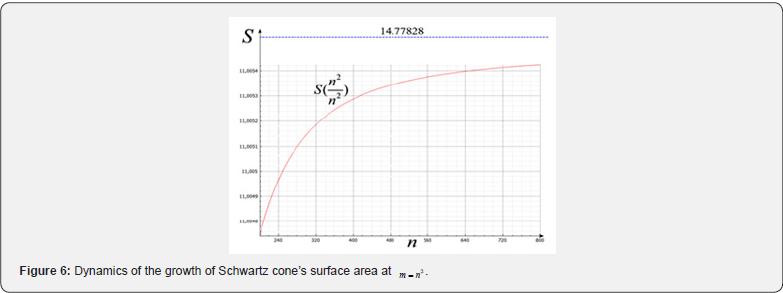
H = 1 and radius R = 1 at m = n2 , while 200 ≤ n ≤ 800 : (Figure 6).
. The following Figure
6 shows the behavior of Schwartz cone’s surface area with height
H = 1 and radius R = 1 at m = n2 , while 200 ≤ n ≤ 800 : (Figure 6).
Figure 6 shows that the area of Schwartz cone does not grow
faster than value of an expression 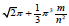 , which in the case
m = n2 is equal to 14.77828. The following Figure 7 shows that the
area S tends to infinity at m = n2.5 about the same rate as the
function
, which in the case
m = n2 is equal to 14.77828. The following Figure 7 shows that the
area S tends to infinity at m = n2.5 about the same rate as the
function 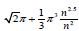 : (Figure 7).
Thus, Figure 5, 6 and 7, as well as inequality (12), show a fairly
good correlation between the area of lateral surface of Schwartz
cone and the limit (1).
: (Figure 7).
Thus, Figure 5, 6 and 7, as well as inequality (12), show a fairly
good correlation between the area of lateral surface of Schwartz
cone and the limit (1).
Thus, Figure 5, 6 and 7, as well as inequality (12), show a fairly good correlation between the area of lateral surface of Schwartz cone and the limit (1).

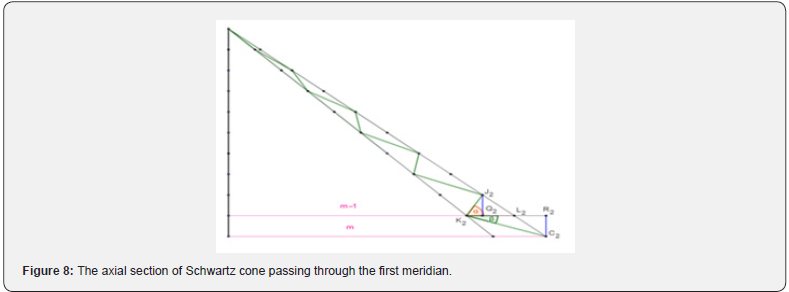
In the case when m = n2 the area limit of Schwarz cylinder with H = R = 1 at m,n→∞was equal to ≈ 31.636 . A natural question arises related to polyhedral surfaces of Schwartz cone, namely: what values do the angles between the faces with a common base tend to (it is clear that the angles along the meridians will already be different)? To answer this question, let’s consider Figure 8. Again, let’s assume that the number of layers is an even number (Figure 8).
To begin with, let’s explore the angle  between
the penultimate and last layer while striving for a ratio
between
the penultimate and last layer while striving for a ratio 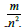 of
one. Note that that n = 2k ⇒m = 4k2 , when m striving for infinity,
it remains an even number. Otherwise, the angle
of
one. Note that that n = 2k ⇒m = 4k2 , when m striving for infinity,
it remains an even number. Otherwise, the angle  , when moving from even m to odd, would change the vertex 2 K to 2 L
and, obviously, strive for its value other than the value of an angle
, when moving from even m to odd, would change the vertex 2 K to 2 L
and, obviously, strive for its value other than the value of an angle
 . It follows from the equality
. It follows from the equality 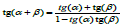 that to
find the angle α + β , it is enough to find tg(α ) and tg(β ) . It is clear
that tg(α ) is easy to find from a right-angled triangle
that to
find the angle α + β , it is enough to find tg(α ) and tg(β ) . It is clear
that tg(α ) is easy to find from a right-angled triangle 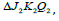 ,
given that
,
given that  namely:
namely:
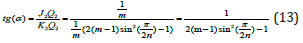
Similarly, from a right-angled triangle ΔK2C2R2 we will find tg(β ) :

Thus, taking into account formulas (13), (14) and equalitym = n2 , the following limit can be found


It follows from formula (15) that the critical angle between
the faces with a common base lying in last and penultimate layers
is approximately equal 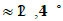 . Now we can answer the
question of what values all angles between faces with a common
base lying on the same meridian tend to. For the convenience of
calculations, we will assume that the height of the cone is divided
into parts m = 2l . Let ‘s take a point
. Now we can answer the
question of what values all angles between faces with a common
base lying on the same meridian tend to. For the convenience of
calculations, we will assume that the height of the cone is divided
into parts m = 2l . Let ‘s take a point  on the axis of
cone, given that l > p and 0 < h ≤ p . The point x is selected
in such a way that the section passing through it for l → ∞
separates the even and odd layers when they are listed from top to
bottom. Formally, the position of the point x on the axis of the cone
does not depend on m , however, the point x is selected in such a
way that by its coordinate, it is possible to find out the numbers of
layers that it will divide at any m given time, given that m = 2l
. Indeed, let the point x separate the layers with numbers i and
on the axis of
cone, given that l > p and 0 < h ≤ p . The point x is selected
in such a way that the section passing through it for l → ∞
separates the even and odd layers when they are listed from top to
bottom. Formally, the position of the point x on the axis of the cone
does not depend on m , however, the point x is selected in such a
way that by its coordinate, it is possible to find out the numbers of
layers that it will divide at any m given time, given that m = 2l
. Indeed, let the point x separate the layers with numbers i and
i +1, then
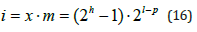
and
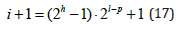
Looking at Figure 9, you can get formulas similar to formulas 13 and 14 obtained earlier. Exactly:


From formulas 18, 19, taking into account the equality of 16 and the fact that m = n2 we get the following equality:
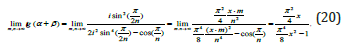
Let’s introduce a notation γ :=α + β , then the function from formula (20) can be written as follows:

The dependence graph from formula (20) for 0 < x < 1is shown in the following Figure 10.
On the graph, the vertical asymptote
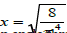 corresponds
to transition of critical (limit) values of an angle through
corresponds
to transition of critical (limit) values of an angle through
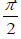 . The
table of function values (together with the corresponding values
of critical (limit) angles in degrees) has the form (Table 1).
. The
table of function values (together with the corresponding values
of critical (limit) angles in degrees) has the form (Table 1).
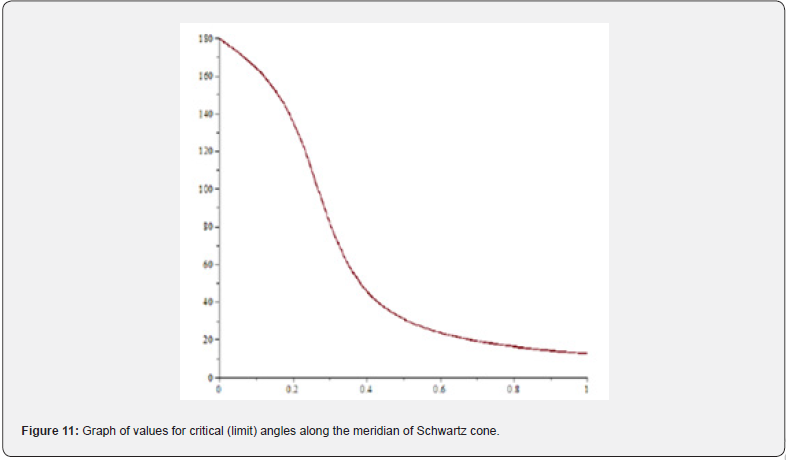
The approximate value of singular point 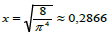 .
.

Then, using the properties of tangent and arctangent functions, from (21) we easily obtain the function of critical (limit) angles between the faces (omitting the limit sign already) as follows:
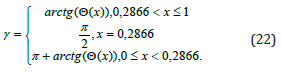
The graph of function γ is shown in the following Figure 11 (its values – the values of critical (limit) angles are located along the ordinate axis, indicated in degrees and fully consistent with the data from Table 1.
We have analyzed above the case m = n2 . A natural question arises: what will happen if m and n are connected by a ratio m = s ⋅ n2 , where s > 0 is some real number?
Then, taking into account (21), (22) and elementary transformations, the function of critical (limit) angles takes the form:
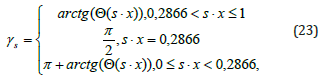
where we add a parameter as a subscript to its designation. Below are graphs of this function for cases of different values of parameter s equal to 0,04; 0,1; 0,5, 1, 2, 5,10, accordingly (the values of function are again located along the ordinate axis) (Figure 12).

At the same time, there are special points at the intersections of graphs with a horizontal line corresponding to the value of critical (limit) angle of 90 degrees. These are the points whose abscesses are given by the ratio s ⋅ x = 0,2866 of (23) for specific values of the parameter s. It is also necessary to take into account that since m is the number of planes parallel to the base of Schwarz cone (that is, an integer), and n is the number of polygons vertices in sections of this cone parallel to the base (also an integer, as thus n2 ). Then when choosing, for example, a specificm and n so the multiplying the integer n2 by the coefficient s should again give an integer m , despite the desire for m and n to infinity. An experimental study of growth areas dynamics for polyhedral lateral surfaces of Schwartz cylinder and cone made it possible to identify the bifurcation point of growth for these linear surfaces. Such a numerical characteristic is the number 2. A parallel study shows that the same number will be the bifurcation point for sphere and torus, but these will already be surfaces with Gaussian curvature other than zero (for ruled surfaces, the Gaussian curvature is zero). This creates a “problem area” for identifying patterns of bifurcation points appearance for surfaces.
An Experimental Study of Creative Thinking
For confirmation of proposed technology effectiveness were organized and conducted in a specialized secondary school some series of elective, laboratory and computational classes and elective courses in mathematics based on the development of elements of modern achievements in science. The content of research activity of school students was concerned with fractal geometry, Schwarz cylinder and cone, methods of encoding and encrypting information, fuzzy logic and fuzzy sets. At the same time, the effect of school student’s creativity developing was measured using the method of “circles” by E Vartegg (undergraduate student K. Chubukova). The results of an experiment showed that the experimental group of school students had an increased creativity indicators during the study of fractal curves on Schwartz cylinder (Table 2). Namely, fluency, flexibility, originality and creative imagination coefficient increased by 9%, 28%, 36% and 24% respectively.

Discussion
The problem of “avoiding complexity” and the tendency to simplify the processes of mathematical abstractions mastering, unfortunately, is practically resolved in modern mathematical (and not only) education and teacher training [22-24]. These trends are reflected in their research by French philosopher Morin E [11], Santos J [6]. German philosopher Mainzer K [20] convincingly demonstrates that in the modern world a transition from linear thinking to nonlinear thinking is necessary, especially in the upbringing of the younger generation. Morin E already at the beginning of the XXIst century draws attention to the need for a fundamental reform of thinking: “The reform of thinking is a key anthropological and historical problem. Never in the history of mankind has the responsibility for thinking and culture been as crucial as it is today. Complex thinking is not the replacement of simplicity with complexity, but the implementation of a continuous dialogue between simple and complex” [11]. Therefore, the paradigm of complex systems and knowledge mastering becomes relevant as a factor of an intellectual development of school students against the background of an emotional response to the applied effect and mathematical and computer modeling symbiosis in teaching mathematics during school student’s search and research activities. In this article, for the first time, the technology and methodology of complex systems and knowledge mastering in teaching mathematics are developed based on the manifestation of synergy for the study of generalized constructs on polyhedral surfaces of Schwartz cone. Thus, an alternative to the “simplification” paradigm is presented with a proven effect of school student’s intellectual operations developing. We remark the significant development of thinking during complex knowledge learning and school student’s motivation increasing to study and apply mathematics.
Conclusion
Thus, the content, stages, technology and computer design of generalized constructs studying for identifying the essence for one of “problem zones” of school mathematics (surface area) are identified and characterized. Nonlinear dynamics details of an area’s growth of polyhedral complexes triangulations of lateral surface of Schwartz cone are presented by means of computer and mathematical modeling. Bifurcation points, basins of attraction, computational procedures and fluctuations of state parameters, computer design and side results of lateral surface area of Schwartz cone are identified and characterized. Hierarchies of forms and means of school students’ research activities are built resource and laboratory calculation classes, complexes of multistage mathematical and information tasks, design methods and network interaction. School student’s creative developing and motivation growth on complex system and knowledge research are shown.
References
- Smirnov EI (2012) Founding of experience in vocational preparing and innovative activity of a teacher. Yaroslavl Kansler pp. 654.
- Smirnov EI, Bogun VV, Uvarov AD (2016) Synergy of mathematical education: Introduction to Calculus. Yaroslavl Kansler pp. 216.
- Tongxin Li, Weiping W, Xiaobo L, Tao W, Xin Z, et al. (2023) Embedding Uncertain Temporal Knowledge Graphs. Mathematics 11(3): 775.
- Dvoryatkina SN, Shcherbatykh SV, Smirnov EI (2021) Technological stages of Schwartz cylinder’s computer and mathematics design using intelligent system. Special Issue on Multidisciplinary Innovation in Engineering Science & Technology organized by Advances in Science, Technology and Engineering Systems Journal 6(1): 447-456.
- Smirnov EI, Uvarov AD, Tikhomirov SA (2024) The manifestation of synergy in the study of multy-stage mathematical and information tasks based on the parameterization method. Continuum Maths Informatics Education 1(33): 18-33.
- Santos J, Figueiredo AS, Vieira M (2019) Innovative Pedagogical Practices in Higher Education: An Integrative Literature Review. Nurse Education Today 72: 12-17.
- Haken H (1996) Principles of Brain Functioning. A Synergetic Approach to Brain Activity, Behavior and Cognition. Berlin Springer.
- Mandelbrot B (2002) Fractal Geometry of Nature. Moscow, Institute of Computer Research pp. 656.
- Prigozin I (1964) Nonequilibrium Statistical Mechanics. Moscow, Mir.
- Podyakov AN (2015) Educational psychology in terms of novelty, complexity, uncertainty. Psychological research. Moscow, Higher school of Economics p. 10.
- Morin E (2005) Method. Nature of Nature. Moscow Progress–Tradition pp. 464.
- Smirnov EI (1997) Technology of Visual Modeling of Teaching mathematics. Yaroslavl YSPU pp. 323.
- Afanasyev VV, Smirnov EI, Povarenkov YP, Shadrikov VD (2002) Teacher Training in Mathematics: Innovative Approaches. Moscow Gardariki pp. 383.
- Sekovanov VS (2016) Elements of the Theory of Discrete Dynamical Systems. S-Petersburg Lan pp. 180.
- Ostashkov VN, Smirnov EI, Belonogova EA (2016) Education Sinergy in Research of Attractors and Basins of Nonlinear Mapping Attraction. Yaroslavl Pedagogical Bulletin 6: 146-157.
- Dvoryatkina SN, Smirnov EI (2016) Evaluation of the synergistic effects of integration of knowledge and activities on the basis of computer simulation. Modern information technologies and IT education. Moscow MSU p. 35-42.
- Smirnov EI, Uvarov AD, Smirnov NE (2017) Computer design of nonlinear growth of "areas" of irregular cylinder of Schwartz. Eurasian scientific review 30(8): 35-55.
- Dvoryatkina SN, Melnikov RV, Smirnov EI (2017) Technology of synergy manifestation in the research of solution’s stability of differential equations system. European Journal of Modern Education 6(4): 684-699.
- Schwartz HA (1890) Sur une définition erronée de l’aire d’une surface courbe: Gesammelte Mathematische Abhandlungen 1: 309-311.
- Mainzer К (1996) Thinking in Complexity: The Complex Dynamics of Matter, Mind, and Mankind: 2nd and extended Edn, Springer, New York.
- Maaliw RRIII (2020) Adaptive virtual learning environment based on learning styles for personalizing e-learning system: design and implementation. International Journal of Recent Technology and Engineering 8(6): 3398-3406.
- Hašková A, Malá E (2019) Training Needs of Technology Teachers in the Context of Teacher s Competences Evaluation. In Sandu A, Ciulei T, Frunza A (Eds), Logos Universality Mentality Education Novelty. European Proceedings of Social and Behavioural Sciences 15: 464-473.
- Kreyk AI, Komf EV (2019) Synergy Aspects of Organic Modernization. In Anna Yurevna K, Igor Borisovich A, Martin de Jong W, Nikita Vladimirovich M (Eds), Responsible Research and Innovation, European Proceedings of Social and Behavioural Sciences 26: 444-450.






























