Research Article

The Factual Versus Counterfactual Reading of Affirmative Versus Contrapositive Conditionals in Chinese

Moyun Wang* and LiyuanZheng

School of Psychology, Shaanxi Key Laboratory of Behavior and Cognitive Neuroscience, Shaanxi Normal University, China

Submission: May 01, 2020; Published: May 21, 2020

*Corresponding author: Moyun Wang, School of Psychology, Shaanxi Key Laboratory of Behavior and Cognitive Neuroscience, Shaanxi Normal University, Xi’an 710062, China; Email:-wangmoyun@snnu.edu.cn

How to cite this article: Moyun Wang, LiyuanZheng. The Factual Versus Counterfactual Reading of Affirmative Versus Contrapositive Conditionals in Chinese. 002 Psychol Behav Sci Int J .2020; 15(1): 555901. DOI:10.19080/PBSIJ.2019.10.555901.

Abstract

One experiment examined whether form of logically equivalent conditionals (affirmative versus contrapositive) would affect instance inferences about conditionals. Participants were asked to indicate whether a specific instance referred to by the affirmative conditional (if p then q) or its contrapositive (if not q then not p) is, is possibly, or is not one of the truth-table cases (pq, p¬q, ¬pq and ¬p¬q) (¬ = not). The results revealed (a) the negative conclusion bias that participants more often judged that the instance is not p¬q and is possibly ¬pq in the affirmative versus contrapositive condition, (b) the evidence matching bias that participants more often regarded the instance as pq in the affirmative versus contrapositive condition, and the instance as ¬p¬qin the contrapositive versus affirmative condition, and (c) the affirmative instance bias that participants more often regarded the instance as pq rather than ¬p¬qin the contrapositive condition. Participants tended to make the factual reading of affirmative conditionals and the counterfactual reading of contrapositive conditionals. The reference-equivalent conditionals elicited different instance inferences, and thereby were not mentally equivalent. Finally, we propose a task dependency account for the diverse interpretations of conditionals found in the present and previous studies. It argues that the reading of conditionals is variable and relative, depending on type of conditional reasoning tasks (the possibility judgment task, the truth evaluation task, and the instance inference task), and form of conditionals (affirmative versus negative conditionals). No existing accounts can explain the found diverse interpretations of conditionals.

Keywords: Affirmative conditionals; Contrapositive conditionals; Instance inferences; The factual reading; The counterfactual reading; The task dependency account

Introduction

Conditionals are extensively used in science and everyday life. A current issue about conditionals is what cases a true conditional (if p then q) implies, or what case is an instance that the conditional refers to. This is the reference inference problem of conditionals. We explore a specific reference inference problem as follows. Given that a specific conditional (e.g., If the card is red, then it is round) is true of one instance, people are asked to judge whether the instance is, is possibly, or is not one of the four truth-table cases (pq, p¬q, ¬pq and ¬p¬q) (where, “¬” = not). We refer to such problems as the instance inference task of conditionals. Its inferential direction is contrary to that of the truth evaluation task in the previous literature that ask people to judge whether a conditional is true or false, given that an instance is one of the four truth-table cases [1-5].

Logically, the material conditional, if p then q, implies that the instance is pq or ¬pq or ¬p¬q, but not p¬q. Here, it is noteworthy that the instance is not p¬q does not imply that it is impossibly p¬q, because the conditional is not necessary. Thus, the instance is possibly pq or ¬pq or ¬p¬q. Crucially, that the conditional is true of an instance, does not logically imply that the instance is pq, and is impossibly p¬q. According to the material conditional of classical logic, the conditional if p then q is logically equivalent to its contrapositive if not q then not p, because the two conditionals have the same truth conditions that both are true in each of pq , ¬pq and ¬p¬q, and false in p¬q. The two forms of conditionals both imply pq or ¬pq or ¬p¬q, and thereby have the same references and are equivalent in terms of references. In current research, we treat the two conditionals as equivalent in terms of references rather than other aspects. For a true conditional referring to an instance, the two forms of conditionals both imply that the instance is pq or ¬pq or ¬p¬q, but not p¬q. Both conditionals do not logically imply that the instance is pq, and the instance is impossibly p¬q. It is interesting to investigate how people infer the instance referred to by the conditional and whether people will show differences between instance inferences about the two forms of equivalent conditionals. No previous studies have investigated these issues.

Some previous studies demonstrate that polarity (affirmative versus negative antecedents or consequents) of conditional statements affects conditional reasoning [6-8]. These researchers found the negative conclusion bias that for conditional inferences such as MP, MT, AC, and DA, people tend to draw more determinate clause inferences with negative conclusions given a conditional including affirmative clauses than given a conditional including negative clauses, because the double negation elimination involved in the latter is more difficult than the mental processing involved in the former. The double negation elimination means that when reasoners have to negate a negation or work out the falsity of a negative statement, this will burden the line of reasoning, and their line of inference will become longer and more prone to errors [8]. Polarity biases suggest that polarity form of conditional statements may also affect people’s instance inferences about conditional statements. Because the affirmative conditional has the affirmative antecedent and consequent, whereas the contrapositive conditional has the negative antecedent and consequent, we conjecture that the two forms of affirmative and contrapositive conditionals will differ between instance inferences about both conditionals. In particular, for the instance inference of a conditional, people will more often judge that the instance is not p¬q and is possibly ¬pq in the affirmative conditional if p then q than in the contrapositive conditional if not q then not p, because in the latter the two instance inferences demand the double negation elimination that is difficult to operate.

There are two main accounts for the reference inference about conditionals: the deterministic and probabilistic accounts [9]. The deterministic account, for example, the material conditional account, mental logic [10] and mental model theory [9-11], claims that a true conditional tolerates no exceptions (p¬q cases), that is, it is deterministic. Probabilistic accounts claim that a true conditional is believable (highly probable but tolerating exceptions) [9,12-16].

The mental model theory (henceforth: MMT) has recently undergone a major revision [17]. In the revised version, a basic conditional is true only if the three truth table cases, pq, ¬pq and ¬p¬q, are all possible and p¬q is impossible. Therefore, MMT predicts that the true affirmative conditional referring to an instance implies that the instance has the conjunction of the three possibilities (pq, ¬pq, ¬p¬q), and that p¬q is false in all three possibilities, and thereby must not be the case. The corresponding contrapositive conditional has the same possibilities as the affirmative conditional.

The probabilistic, suppositional account explains the meaning of conditionals as hypothetical thinking [3,18-21]. A conditional (if p then q) expresses people’s subjective degree of belief in a conditional and relies on the Ramsey test in which people hypothetically add the antecedent to their stock of knowledge and judge the likelihood of the consequent. People judge the probability of a conditional assertion according to the conditional probability of the consequent given the antecedent, P(q|p). Thus, people interpret a true conditional as highly believable (so tolerating some exceptions) rather than logically valid or necessary [2,18,19,22,23-27]. Thus, for a true conditional, the suppositional account generally does not rule out the possibility of p¬q, it is just improbable. According to the Jeffrey table [28[, when information about P(q|p) is available, the suppositional conditional can have the calculation of P(q|p) given the false antecedent cases (Jeffrey, 1991), as is confirmed by Wang & Zhu’s study [29]. Thus, it is reasonable to regard these cases (¬pq, ¬p¬q) as possible. Therefore, the suppositional conditional predicts that for both the true affirmative conditional and its contrapositive, each truth table case is possible, but is not definitely the case. Both conditionals also have the same possibilities. Some previous studies have examined possibility inferences from conditionals by using the possibility judgment task. In such tasks, given an indicative conditional, individuals tend to regard each of pq, ¬pq and ¬p¬q cases as possible, and regard p¬q cases as impossible [4,9,30,31,32]. These findings show that possibility inferences from conditionals accord with MMT. However, such tasks provide participants with the forcechoice dichotomous response format (“possible” and “impossible”). The “impossible” option deviates from the logical answer that p¬q cases do not exist and are not impossible given a true conditional. Thus, the force-choice dichotomous response format is not appropriate to investigate the reference inference about conditionals. Wang, Yin & Zheng [33] examined people’s modal inferences about conditionals using a three-option response format. They asked participants to judge whether the instance referred to by a true conditional is necessarily, possibly, or impossibly one of the four truth table cases. Both the “is necessarily” and “is impossibly” option deviate from the respective logical norms because an indicative conditional does not logically imply that the instance is necessarily or impossibly one of the four truth table cases. Thus, the three-option response format is not appropriate to investigate the general reference inference of conditionals either. Overall, these existing studies did not use the appropriate response format that is consistent with the logical implication of conditionals. Their results may not be conclusive.

No previous studies have examined the instance inference problem of conditionals. The suppositional account and MMT make different predictions for instance inferences. MMT predicts that only p¬q should not be the case. In contrast, the probabilistic, suppositional account views p¬q as possible. Both accounts agree that each of the remaining truth table cases is possible for the case but is not definitely the case. The two accounts predict that there will be no differences between instance inferences about affirmative and contrapositive conditionals because both conditionals have the same possibilities. The present experiment used the response format consistent with the logical constraint of conditionals. The experiment used the instance inference task that asked participants to judge whether one instance referred to by a true indicative conditional is, is possibly, or is not each of the four truth table cases. We refer to this response format as the logical response format. The conditional was varied with two equivalent forms: affirmative and contrapositive conditionals. We would compare instance inferences about the two forms of conditionals.

Experiment

Method

Participants: Eighty college students (38 men, 42 women) from Shaanxi Xueqian Normal University in China participated in the experiment. They had not studied any logic course before.

Design and materials: Experiment 1 was a paper-andpencil questionnaire study. We used a 2 (form of conditionals) × 2 (type of conditionals) mixed design where the first factor was between-subjects and the latter factor was within-subjects. Form of conditionals was varied with affirmative indicative conditionals (if p then q) and their contrapositives (if not q then not p). We used two types of conditionals: abstract versus concrete conditionals. Here, we used definitional conditionals as the representative of concrete conditionals because definitional conditionals are extensively used in everyday language. For each type of conditionals, there were two sets of problem materials used. In particular, there were two abstract conditionals (“If the card is round, then it is red” and “If the ball is white, then it is metallic”) and two concrete conditionals (“If the plant is a rose, then it has a thorn” and “If the animal is a bird, then it has wings.”). An abstract conditional does not contact semantic association between its antecedent and consequent. A concrete conditional (e.g.) contacts semantic association between its antecedent and consequent (Johnson-Laird, 2011).

Thus, the questionnaire for each group involved four problems that were arranged in the counterbalanced manner. Each problem contained four questions about truth table cases. The four questions were also arranged in the counterbalanced manner. Two examples of the problems with affirmative conditionals are presented as follows. Here is an English version translated from the original Chinese version.

Instruction

Please complete the following problems in the given order. Please tick your answer to each question.

Problem one

There is a card. For the card, the assertion “if the card is round, then it is red”, is true.

Please judge whether the card is the respective cases below.

i. (is, is possibly, is not ) a non-round non-red card.

ii. (is, is possibly, is not) a non-round red card.

iii. (is, is possibly, is not) a round non-red card.

iv. (is, is possibly, is not) a round red card.

Problem two

There is a plant. For the plant, the assertion “if the plant is a rose, then it has thorns”, is true.

Please judge whether the plant is the respective cases below.

i. (is, is possibly, is not) not a rose and it has no thorns.

ii. (is, is possibly, is not) not a rose and it has thorns.

iii. (is, is possibly, is not ) a rose and it has no thorns.

iv. (is, is possibly, is not) a rose and it has thorns.

For the problems with contrapositive conditionals, we used the contrapositive conditionals (e. g, if the card is not red, then it is not round) to replace the respective affirmative conditionals, and reversed the arrangement order of the two clauses in each truth table case in the affirmative conditional problems. The other aspects of the contrapositive conditional were identical to those of the affirmative conditional. The above experimental design aimed to compare instance inferences about affirmative and contrapositive conditionals.

Procedure

We conducted the experiment in a quiet classroom. Every participant received the questionnaire on a sheet of paper and a pen to fill it out. They took about 10 minutes to complete the task.

Results

In each type of conditionals, the results showed no obvious differences between the two kinds of problem contents. Thus, the results were collapsed across problem contents. Table 1 shows the overall results. For both the affirmative and contrapositive conditionals, the correct answers for pq, p¬q, ¬pq and ¬p¬q cases were “is possibly”, “is not”, “is possibly”, and “is possibly”, respectively. In the affirmative condition, the majority of participants gave the erroneous answer “is” for pq cases and the correct answers for p¬q, ¬pq and ¬p¬q cases. In the contrapositive condition, the majority of participants gave the erroneous affirmative answer “is” for pq cases and the correct answers for p¬q cases, but the answers for ¬pq and ¬p¬q cases were scattered. For the contrapositive conditionals, pq cases elicited more affirmative answers (“is”) than ¬p¬q cases.

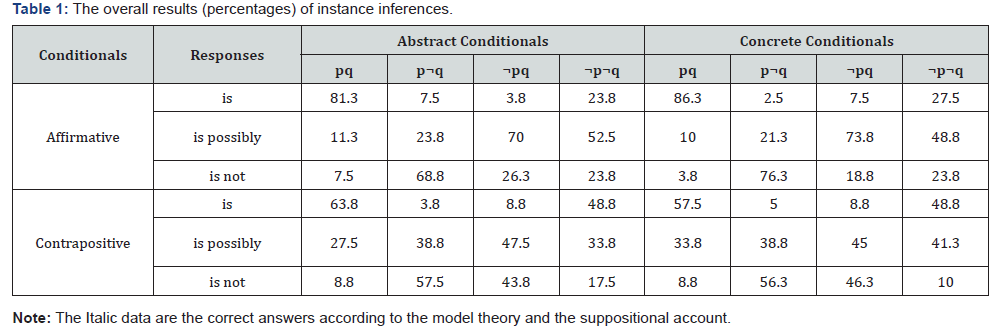
The two types of conditionals showed no obvious differences in performance. Thus, type of conditionals did not affect participants’ performance. Form of conditionals affected participants’ performance on each truth table case. The χ2 test of independence showed that in each type of conditionals, the rate of affirmative responses (“is”) to pq cases was larger in the affirmative condition than in the contrapositive condition (for the abstract condition, χ2 (1) = 6.14, W = 0.20, p < .05; for the concrete condition, χ2 (1) = 16.36, W = 0.32, p < .01). For p¬q cases in each type of conditionals, the rate of negative responses (“is not”) was larger in the affirmative condition than in the contrapositive condition (for the abstract condition, χ2 (1) = 2.18, W = 0.12, p >.05; for the concrete condition, χ2 (1) = 7.16, W = 0.21, p < .05). In each type of conditionals, for both ¬pq and ¬p¬q cases we ran a 2 (the two forms of conditionals) × 3 (the three response options) χ2 test of independence. The results showed that the two forms of conditionals showed obvious differences in response distribution (In the abstract condition, χ2 (2) = 8.55, W = 0.23, p < .01 for ¬pq cases; χ2 (2) = 10.92, W = 0.26, p < .01 for ¬p¬q cases. In the concrete condition, χ2 (2) = 14.95, W = 0.31, p < .01 for ¬pq cases; χ2 (2) = 9.72, W = 0.25, p < .01 for ¬p¬q cases). For ¬pq cases, the affirmative condition elicited more possible responses (“is possibly”) than the contrapositive condition, whereas the contrapositive condition elicited more negative responses (“is not”) than the affirmative condition. For ¬p¬q cases, the affirmative condition elicited more possible responses than the contrapositive condition, whereas the contrapositive condition elicited more affirmative responses than the affirmative condition. Overall, instance inferences for each truth table case differed between the affirmative and contrapositive condition. This is not consistent with the prediction of the material conditional account, MMT and the suppositional account. These account all predict that instance inferences should not differ between the affirmative and contrapositive conditional because the references of both conditionals are equivalent.

In the affirmative condition, participants more often judged that the instance referred to by an affirmative conditional is the matching case pq (more than 80%) rather than the mismatching case ¬p¬q (less than 30%). This means that the affirmative conditional refers to the affirmative instance and thereby has the factual evidence. Thus, they showed the factual reading of the affirmative conditional. In the contrapositive condition, participants more often judged that the instance referred to by a contrapositive conditional is the mismatching case pq (63.8% for abstract conditionals and 57.5% for concrete conditionals) rather than the matching case ¬p¬q (48.8% for both abstract and concrete conditionals). This means that the contrapositive conditional refers to the instance pq and is a counterfactual statement. Thus, they showed the counterfactual reading of contrapositive conditionals.

Discussion

The present results revealed that the two kinds of reference- equivalent conditionals elicited different instance inferences. Form of conditionals yielded a significant effect on instance inferences for each truth table case. Participants showed obvious differences between instance inferences about affirmative and contrapositive conditionals. They showed the factual reading of affirmative conditionals and the counterfactual reading of contrapositive conditionals. These findings are novel on the whole. The found differences are beyond the prediction of the material conditional account, MMT and the suppositional account. These account all predict no differences between instance inferences about affirmative and contrapositive conditionals because both conditionals have the same references. Next, we explain the effect of form of conditionals on instance inferences for each truth table case and explore the theoretical implications of the present findings. Finally, we discuss the relation to previous research.

Explanations for the present findings

For instance inferences, participants more often judged that the instance is not p¬q and is possibly ¬pq in the affirmative conditional if p then q than in the contrapositive conditional if not q then not p. Participants showed negative conclusion bias on instance inferences for both p¬q and ¬pq. It implies that in the contrapositive condition there was the difficulty of the double negation elimination that reduced correct instance inferences for p¬q and ¬pq. These findings are consistent with our predictions and the previous finding of negative conclusion bias in conditional reasoning, confirming that polarity of conditionals also affects instance inferences for p¬q and ¬pq. For instance inferences for pq and ¬p¬q, participants more often judged that the instance is pq in the affirmative conditional than in the contrapositive conditional, and that the instance is ¬p¬q in the contrapositive conditional than in the affirmative conditional. Participants were more likely to judge that the instance referred to by an affirmative conditional is pq, which is the matching evidence for the affirmative conditional, and that the instance referred to by a contrapositive conditional is ¬p¬q, which is the matching evidence for the contrapositive conditional. These instance inferences diverge from the logical norms and the predictions of MMT and the suppositional account, and thereby were biased. Participants tended to regard the instance referred to by a conditional as the matching case, showing the evidence matching bias. This implies that they based their erroneous instance inferences on the evidence matching heuristic. This heuristic means that the matching case is the evidence for the conditional such that people may intuitively associate the conditional with the matching case and further infer that the instance is the matching case. The evidence matching heuristic leads to the evidence matching bias that people tend to judge that the instance referred to by a conditional is the matching case for the conditional.

It could be argued that MMT can provide an alternative account of for the evidence matching bias. According to MMT, people may only initially represent the explicit pq (or ¬p¬q) model but forget about the other alternative cases until explicitly asked about them when they judge that they are also possible. This initial representation may result in the evidence matching bias. However, in the present instance inference problem, the matching case and the possibility for ¬pq were simultaneously present. Consequently, possible inferences for ¬pq must have already resulted in explicit models which formed the context for instance inferences for the matching case pq (or ¬p¬q). According to MMT, the explicit models of ¬pq should render the matching case not affirmative. Nonetheless, participants still made affirmative inferences for the matching case, rather than based their inferences on the explicit models for ¬pq. Therefore, the initial representation account is not viable. More importantly, the initial representation does not imply that the instance is the matching case, because the matching case is only possible according to MMT. Consequently, MMT is unable to explain the evidence matching bias.

The evidence matching bias showed a difference between the affirmative and contrapositive condition. In the affirmative condition, most participants regarded the matching case pq as the instance (that is, factual), showing the factual reading of affirmative conditionals. In each type of conditionals, the rate (less than 50%) of affirmative inferences for the matching case ¬p¬q in the contrapositive condition was less than the rate (more than 80%) of affirmative inferences for the matching case pq in the affirmative condition. This means that contrapositive conditionals were less likely to elicit the evidence matching bias than affirmative conditionals. This difference was due to the unique reading of contrapositive conditionals. In the contrapositive condition, participants made more affirmative inferences for pq cases (about 60%) than for ¬p¬q cases (less than 50%). They were more likely to judge that the instance referred to by a contrapositive conditional is in fact the mismatching case pq rather than the matching case ¬p¬q, showing the affirmative instance bias. They showed the counterfactual reading of contrapositive conditionals. This was different from the factual reading of affirmative conditionals. Consequently, the counterfactual reading of contrapositive conditionals resulted in that the evidence matching bias was less likely to occur in the contrapositive condition.

In the present instance inference task, most participants showed the factual reading of affirmative conditionals, whereas the majority of participants showed the counterfactual reading of contrapositive conditionals. The former finding is consistent with the previous finding that in modal inferences from conditionals participants tended to judge that the instance referred to by a affirmative conditional must be pq (Wang, Yin, & Zheng 2018). The latter finding is novel. The two findings demonstrate that the logically equivalent (affirmative versus contrapositive) conditionals elicit different instance inferences and thereby are not mentally equivalent in terms of references. Both findings diverge from the predictions of the material conditional account, MMT and the suppositional account, and thereby are biased. These accounts all predict that the instance referred to by a conditional should be uncertain.

What causes the counterfactual reading of contrapositive conditionals? We explain it as follows. In Chinese, the contrapositive of an affirmative conditional has the same linguistic form as the negative conditional (e. g, if the card is not red, then it is not round). The contrapositive and negative conditional share the same linguistic representation. Here, it is noteworthy that the negative conditional is different from the negated conditional (e. g, if the card is red, then it is not round). The negative and counterfactual conditional both take the indicative mood such that the negative conditional is ready to be confused with and be mistaken for the counterfactual conditional that refers to a factual affirmative situation with both p and q. Consequently, in Chinese, for an affirmative conditional (if p then q), its contrapositive (if not q then not p) as a negative conditional is ready to be mistaken for the counterfactual conditional (if not q then not p). The essence is that in Chinese, negative conditionals are ready to be confused with counterfactual conditionals so as to elicit the counterfactual reading. However, there is no confusion of negative and counterfactual conditionals in English because both take different moods. In English, the negative conditional such as the contrapositive conditional takes the indicative mood, whereas the counterfactual conditional takes the subjunctive mood [34,35]. Thus, we predict that in English, the negative conditional such as the contrapositive of an affirmative indicative conditional is not ready to be mistaken for the counterfactual conditional in the subjunctive mood. This is confirmed by the first experiment in Thompson & Byrne’s article [35].

Overall, whether people readily mistake the negative conditional (or the contrapositive of an affirmative indicative conditional) for the counterfactual conditional will differ between Chinese and English, because the two languages differs in terms of counterfactual representations. There is the confusion of negative and counterfactual conditionals in Chinese, but not in English. The counterfactual reading will be more likely to occur in Chinese populations than in English populations. It is interesting to investigate this possible difference in future research.

Theoretical implications

For the present experimental design, if we treated the contrapositive conditional (if not q then not p) as the negative conditional and the affirmative conditional as the contrapositive of the negative conditional, the present manipulation of affirmative conditionals (if p then q) versus their contrapositives (if not q then not p) became into the manipulation of negative conditionals (if not q then not p) versus their contrapositives (if p then q). So, the results of the negative conditionals and their contrapositives would be the results of the contrapositives and affirmative conditionals in the present experiment, respectively. Thus, participants would show the counterfactual reading of the negative conditionals and the factual reading of their contrapositives. It follows that in Chinese, people tend to make the counterfactual reading of negative conditionals and the factual reading of their contrapositives.

Overall, in Chinese, polarity of conditionals modulates the reading of conditionals and their contrapositives in the present instance inference task. People tend to make the factual reading of affirmative conditionals and the counterfactual reading of their contrapositives, and to make the counterfactual reading of negative conditionals and the factual reading of their contrapositives. These reading patterns have a commonness that people tend to make the factual reading of affirmative conditionals and the counterfactual reading of negative conditionals. Thus, we can conclude that in Chinese people tend to make the factual reading of affirmative conditionals and the counterfactual reading of negative conditionals in the instance inference task. The present experiment found that the logically equivalent (affirmative versus contrapositive) conditionals elicit different instance inferences and interpretations, and thereby are not mentally equivalent. This finding is consistent with the previous finding that the majority of participants thought the contrapositive conditional does not follow from a given affirmative conditional [36]. These findings demonstrate that affirmative and contrapositive conditionals are not mentally equivalent. This conclusion is beyond the material conditional account, MMT and the suppositional account. These accounts all predict that both conditionals should be equivalent in terms of references, that is, have the same references.

The factual reading of affirmative conditionals means that people tend to read an affirmative conditional as factual in that it refers to a affirmative instance pq. The counterfactual reading of a negative conditional (if not p then not q) means that the conditional is a counterfactual supposition referring to the factual situation pq. The counterfactual conditional is consistent with the suppositional account. The factual and counterfactual reading both refer to an affirmative fact. This finding in the instance inference task is different from the previous finding that in the truth evaluation task, given that the instance referred to by a conditional is a false antecedent case, people may judge that the suppositional conditional is true, showing the suppositional [29]. Moreover, the factual and counterfactual reading of conditionals in the instance inference task are also different from the previous finding that in the possibility judgment task people generally think that the basic conditional implies the three possibilities (pq, ¬pq, ¬p¬q), showing the possibility reading predicted by the model theory [4,9,30,31-33]. The above two differences suggest that the reading of conditionals depends on type of conditional reasoning tasks (the instance inference task, the truth evaluation task, and the possibility judgment task).

Overall, in Chinese there are four kinds of the reading of conditionals: the possibility, suppositional, counterfactual, and factual reading. The model and suppositional reading both need not referring to an affirmative instance. The possibility reading occurs in the possibility judgment task. The suppositional reading occurs in the truth evaluation task. The counterfactual reading of negative conditionals and the factual reading of affirmative conditionals occur in the instance inference task. The factual and counterfactual reading involve certain factual references, which may be absent in the suppositional and possibility reading. On the basis of these diverse interpretations, we propose a task dependency account for the reading of conditionals. Its basic idea is that the reading of conditionals is variable and relative, depending on type of conditional reasoning tasks (the possibility judgment task, the truth evaluation task, and the instance inference task), and form of conditionals (affirmative versus negative conditionals). In particular, type of conditional reasoning tasks constrains the interpretation of conditionals, and different conditional reasoning tasks tend to elicit different interpretations. The possibility judgment task tends to elicit the possibility reading, the truth evaluation task tends to elicit the suppositional reading, and the instance inference task tends to elicit the factual reading of affirmative conditionals and the counterfactual reading of negative conditionals. We for the first time demonstrate the diversity of the interpretation of conditionals. No existing accounts of conditionals can explain this diversity. The task dependency account is an important contribution to research on the interpretation of conditionals.

Acknowledgement

This work was supported by National Natural Science Foundation of China under General Grant .

References

1. Baratgin J, Over DE, Politzer G (2013) Uncertainty and de Finetti tables. Thinking & Reasoning 19: 308-328.
2. Over DE, Baratgin J (2017) The "defective" truth table: Its past, present, and future. In: Galbraith N, (Ed.), The Thinking Mind: A Festschrift for Ken Manktelow. Routledge Publisher, United Kingdom.
3. Politzer G, Over DE, Baratgin J (2010) Betting on conditionals. Thinking & Reasoning 16: 172-197.
4. Schroyens W (2010) A meta-analytic review of thinking about what is true, possible, and irrelevant in reasoning from or reasoning about conditional propositions. European Journal of Cognitive Psychology 22: 897-921.
5. Wason P, Johnson-Laird PN (1972) Psychology of reasoning: Structure and content. Batsford, London, United Kingdom.
6. Evans J St BT, Clibbens, J, Rood B (1995) Bias in conditional inference: Implications for mental models and mental logic. Quarterly Journal of Experimental Psychology 48A: 644-670.
7. Evans J St BT, Handley SJ (1999) The role of negation in conditional inference. Quarterly Journal of Experimental Psychology 52A: 739-769.
8. Schroyens WJ, Schaeken W, d'Ydewalle G (2001) The processing of negations in conditional reasoning: A meta-analytic case study in mental model and/or mental logic theory. Thinking & reasoning 7(2): 121-172.
9. Goodwin GP (2014) Is the basic conditional probabilistic? Journal of Experimental Psychology: General 143(3): 1214-1241.
10. Rip LJ (1994) The psychology of proof. MIT Press, Cambridge, MA, USA.
11. Johnson-Laird PN, Byrne RMJ (2002) Conditionals: A theory of meaning, pragmatics, and inference. Psychological Review 109: 646-678.
12. Evans J St BT, Handley SJ, Over DE (2003) Conditionals and conditional probability. Journal of Experimental Psychology: Learning, Memory, and Cognition 29: 321-335.
13. Fugard AJB, Pfeifer N, Mayerhofer B, Kleiter GD (2011) How people interpret conditionals: Shifts toward the conditional event. Journal of Experimental Psychology: Learning, Memory, and Cognition 37: 635-648.
14. Liu I, Lo K, Wu J (1996) A probabilistic interpretation of “if-then”. Quarterly Journal of Experimental Psychology: Human Experimental Psychology 49(A): 828-844.
15. Oaksford M, Chater N (2009) Precis of Bayesian rationality: The probabilistic approach to human reasoning. Behavioral and Brain Sciences 32: 69-84.
16. Oberauer K, Wilhelm O (2003) The meaning(s) of conditionals: Conditional probabilities, mental models, and personal utilities. Journal of Experimental Psychology: Learning, Memory, and Cognition 29: 680-693.
17. Johnson Laird PN, Khemlani S, Goodwin GP (2015) Logic, probability, and human reasoning. Trends in Cognitive Sciences 19(4): 201-214.
18. Evans J St BT (2007) Hypothetical thinking: Dual processes in reasoning and judgement. Psychology Press (Vol. 3)
19. Evans J St BT, Over DE (2004) If. Oxford University Press, Oxford, England, United Kingdom.
20. Evans J St BT, Over DE, Handley SJ (2005) Suppositions, extensionality, and conditionals: A critique of the mental model theory of Johnson-Laird and Byrne (2002) Psychological Review 112(4): 1040-1052.
21. Over DE, Evans J St BT (2003) The probability of conditionals: The psychological evidence. Mind & Language 18: 340-358.
22. Adams EW (1998) A primer of probability logic. CSLI Publications Stanford, United States.
23. Over DE (2016) The paradigm shift in the psychology of reasoning: The debate. In: L Macchi, M Bagassi, R Viale (Eds.), Cognitive unconscious and human rationality Cambridge, MA: MIT Press, USA, pp. 79-97.
24. Over DE, Cruz N (2017) Probabilistic accounts of conditional reasoning. In: Ball LJ, Thompson VA (Eds.), International handbook of thinking and reasoning. Psychology Press, Hove, United Kingdom.
25. Pfeifer N, Kleiter GD (2009) Framing human inference by coherence-based probability logic. Journal of Applied Logic 7: 206-217.
26. Singmann H, Klauer KC, Over DE (2014) New normative standards of conditional reasoning and the dual-source model. Frontiers in Psychology 5: 316.
27. Skovgaard-Olsen, N, Singmann, H, Klauer KC (2016) The relevance effect and conditionals. Cognition 150: 26-36.
28. Jeffrey RC (1991) Matter of fact conditionals. Aristotelian Society Supplementary 65: 161-183.
29. Wang M, Zhu M (2019) Evidence for the Jeffrey Table: Credibility Ratings for Conditionals Given False Antecedent Cases. Experimental Psychology.
30. Barrouillet P, Grosset N, Lecas JF (2000) Conditional reasoning by mental models: Chronometric and developmental evidence. Cognition 75: 237-266.
31. Barrouillet P, Gauffroy C, Lecas JF (2008) Mental models and suppositional accounts of conditionals. Psychological Review 115: 760-771.
32. Handley SJ, Evans J St BT, Thompson VA (2006) The negated conditional: A litmus test for the suppositional conditional? Journal of Experimental Psychology: Learning, Memory, and Cognition 32: 559-569.
33. Wang M, Yin P Zheng, L (2018) A necessity illusion for modal inferences from conditionals. Thinking & Reasoning 24(3): 366-385.
34. Quelhas AC, Rasga C, Johnson Laird PN (2018) The relation between factual and counterfactual conditionals. Cognitive science 42(7): 2205-2228.
35. Thompson VA, Byrne RM (2002) Reasoning counterfactually: Making inferences about things that didn't happen. Journal of Experimental Psychology: Learning, Memory, and Cognition 28(6): 1154-1170.
36. Pollard P, Evans J St BT (1980) The influence of logic on conditional reasoning performance. Quarterly Journal of Experimental Psychology 32(4): 605-624.
37. Evans J St BT (1998) Matching bias in conditional reasoning: Do we understand it after 25 years? Thinking and Reasoning 4: 45-82.
38. Evans J St BT (2006) The heuristic-analytic theory of reasoning: Extension and evaluation. Psychonomic Bulletin & Review 13(3): 378-395.
39. Edgington D (1995) On conditionals. Mind 104: 235-329.
40. Johnson-Laird PN (2006) Mental models, sentential reasoning, and illusory inferences. Advances in Psychology 138: 27-51.
41. Wang M, Yao X (2018) The dual reading of general conditionals: The influence of abstract versus concrete contexts. Quarterly Journal of Experimental Psychology 71: 859-869.