Oceanography & Fisheries Open access Journal (OFOAJ)

Short Communication

The Seasonally Varying Monsoon Wind May Suppress the Western Boundary Current in the South China Sea

Liang XS*

Center for Ocean-Atmosphere Dynamical Studies, Nanjing Institute of Meteorology, China

Submission: April 22, 2017; Published: June 01, 2017

*Corresponding author: Liang XS, Center for Ocean-Atmosphere Dynamical Studies, Nanjing Institute of Meteorology, 219 Ningliu Blvd, Nanjing,210044, China, Email: sanliang@courant.nyu.edu

How to cite this article: Liang XS. The Seasonally Varying Monsoon Wind May Suppress the Western Boundary Current in the South China Sea. Ocean & fish Open Access J. 2017; 3(1): 555601. DOI: 10.19080/OFOAJ.2017.03.555601

Abstract

Guided by the classical wind-driven circulation theory, there has long been an effort to seek for a western boundary current in the South China Sea. In this study we show that the seasonally varying monsoon wind stress curl may weaken such a current or even prevent it from being generated.

Introduction

The South China Sea (SCS) is the largest marginal sea in the Western Pacific Ocean. Straddling one of the world's busiest shipping routes, it is no doubt of enormous economic value. The surrounding countries, namely, China, Vietnam, the Philippines, Malaysia, and Brunei, have long competing territorial and jurisdictional claims, particularly over rights to exploit the region's vast reserves of oil and gas. The risk of armed clash is significant, making it a military hotspot in the world.

From a scientific viewpoint of oceanography, this region is also of enormous interest. Considering its geometry (a semien closed domain) and the fact that the upper ocean circulation, particularly the southern SCS circulation, is mainly forced by the wind stress curl [1-6,11], it is temptating to make SCS a mini analogy of the world ocean. If this is true, SCS would provide an ideal test bed for the wind-driven circulation theory, one of the most successful theories in physical oceanography-Anyhow, the world ocean is too big to survey, while SCS has the right size.

In a wind-driven world ocean circulation, the most prominent feature is no doubt the existence of a western boundary current, just like Kuroshio in the Pacific and Gulf Stream in the Atlantic [7]. So there has also been a long effort in search for such a boundary current in the SCS; in fact this has been a major objective for many SCS survey projects since decades ago. Indeed, the idea is intriguing. However, it is doubtful that a western boundary current in the normal sense should exist, considering that the circulation is not steadily forced, but driven by the monsoon wind with an annual variability. The temporally varying wind stress curl may drive a circulation quite different from that forced by a steady one, as long studied by, say, Pedlosky [8]. In the following we illustrate the problem with a barotropic quasi- geostrophic (QG) model, the model which Stommel [9] used in his renowned wind-driven circulation theory.

Analysis with an Idealized Quasi-Geostrophic Model

Consider a QG model with a Newtonian friction:

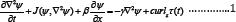
The symbols are conventional. This type of friction was originally considered by Stommel [9]. For simplicity, consider, as a first step, a rectangular domain with a flat bottom. Different from Stommel's model, now the forcing on the right hand side is time varying:

where F1 is the amplitude of the variation and « the angular frequency. This is used to represent the seasonal variability of the monsoon wind forcing.

To see how a periodic wind stress forcing excites the SCS, look at how the linear response may be. The governing equation (1) with the nonlinear terms taken out becomes

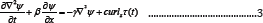
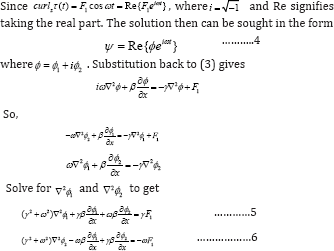
These, together with the vanishing boundary conditions for ɸ and ɸ= should be (ɸ = ɸ₂ = 0 at the boundaries), form a set of Poisson equations. The final solution of Ψ is, therefore,

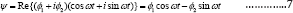
The equation set (5)-(6) can be solved with series expansion. But before moving on, it is beneficial to examine some special cases:

) ω = 0. This corresponds to the steady case. Eq. (6) has only a trivial solution, i.e., ɸ= 0, considering the vanishing boundary conditions and the zero forcing. Eq. (5) is simply the linear Stommel model equa-tion; the solution is the well known pattern with a strong western boundary current.
) y = 0. In this case, the two equations can be decoupled.For example, ɸsatisfies the following equation: 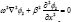which gives a solution without westward intensification. Similar solution appears with ɸ₁
) In the classical Stommel model, the western boundary current results from the β-effect and a very small but nonvanishing but non-vanishing y. In the present case, as one can see from (5) and (6), ω functions like y, though not exactly because these two equations are coupled. So when ω is large, it is expected that the westward intensification may be suppressed. We now check whether this is true.

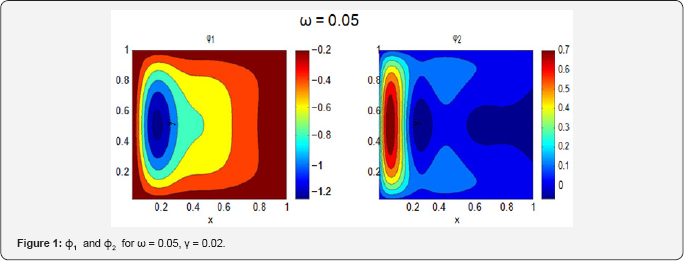
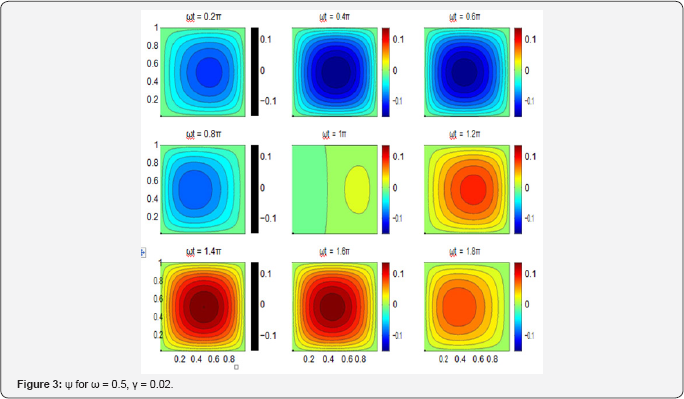
Let the β-effect balance the wind stress curl and take β=F₁=1. Figure 1 shows the resulting ɸ and ɸ₂ with ϒ= 0.02, ω=0.05. This is a solution with westward intensification and, hence, Ψ = ɸ₁ cos ωt -ɸ₂ sin ωt must also be so. However, as ω is increased, the corresponding ɸ1 and ɸ₂ are drastically altered. Figure 2 shows the case with ω=0.5. Observe that ɸ₂ is now nearly symmetric in x, while ɸ₁ even shows some sign of a weak eastern boundary current. The corresponding Ψ is drawn in Figure 3. As one can see, the western boundary current is greatly weakened and may disappear. Moreover, at ωt =0.2Π, 1.2Π, etc., the circulation even shows some sign of intensification toward the eastern boundary.

So the normalized ω will determine the pattern of the circulation pattern. We now give it an estimation. The SCS is located around a latitude at 15° N which yields a typical Coriolis parameter f₀ ≈ 4 x 10-⁵ 1/s and its meridional gradient β₀≈2.2 x 10'¹¹ 1/sm. Choose a length scale L=500km. The time scale T may be determined either by the Ross by wave celerity c~β₀/ɸ2Π/L)² ~0.14m/s, or by the advection speed U, which is estimated to be 0.2m/s [10]. So T~L/U~30 days or L/c ~ 40 days. Normalized by these estimated T's, the period of 365 days is about 12 and 9, yielding an ω=2n/12~0.51 and 0.69, respectively. The stream function is similar to that as shown in Figure 3. If L is chosen to be 1000km, ω becomes much bigger, resulting a circulation with almost no sign of westward intensification.

Conclusion and Discussion

To summarize, with a seasonally varying monsoon wind stress curl, the western boundary current may be greatly weakened or even completely suppressed, provided that the wind frequency is large enough. In the SCS, there could even be instants with a sign of weak intensification in the eastern boundary.

The above treatment did not consider the case of a wind stress curl with a nonzero mean, and the case with a forcing asymmetric in time. But the argument that the temporally varying monsoon wind will weaken the western boundary current still holds. Also ignored is the unique topography in the SCS; the strong topographic beta effect may cause the circulation intensified toward the east near the southern boundary of the basin.

Other factors that may determine the SCS circulation pattern include baroclinicity, domain geometry, wind stress inhomogeneity, etc., which, of course, are not within the scope of this brief study. Here the take-home message is: if no western boundary current appears, it is not a surprise; if there is such a current, the classical theory of steady wind-driven circulation may not be appropriate for its explanation.

Acknowledgement

The supports from National Science Foundation of China (# 41276032), 2015 Jiangsu Jiangsu Program for Innovation Research and Entrepreneurship Groups, Jiangsu Chair Professorship, and National Program on Global Change and Air- Sea Interaction (GASI-IPOVAI-O6) are acknowledged.