Common Method Variance: Statistical Detection and Control
Chongming Yang1, Joseph A. Olsen1, Krista W. Ranby2 and Trenette Clark Goings3
1Brigham Young University, USA
2University of Colorado at Denver, USA
3University of North Carolina at Chapel-Hill, USA
Submission: September 13, 2017; Published: September 19, 2017
*Corresponding author: Chongming Yang, Research Support Center, Social Sciences College, Brigham Young University, USA, Tel: 801-422-5694; Email: chongming_yang@byu.edu.
How to cite this article: Yang, C., Olsen, J. A., Ranby, K. W., Goings, T. C. Common Method Variance: Statistical Detection and Control. OAJ Gerontol & Geriatric Med. 2017; 2(4): 555593 DOI: 10.19080/OAJGGM.2017.02.555593
Abstract
Common Method Variance (CMV) may arise from monomethod measurement of both exogenous and endogenous variables. It has caused concerns about its effects on causal inferences. One way to partition out CMV is specifying a method factor measured by indicators of both the exogenous and endogenous variables in a model. This method is known as Common Method Factor Modeling (CMFM). However, it remained unclear what to expect when CMFM is applied to data with unknown magnitude of CMV, whether the method factor loadings should be estimated freely or with equality constraints, and whether model comparison was viable for detecting CMV. The results of three simulation studies have demonstrated the limitations of detecting CMV with model comparisons, the advantages of power analysis applied to empirical data and Bayesian estimation of CMFM. Specifically, model comparisons usually fail the estimation with misspecified CMFM in small samples; Power analyses through simulating several sample sizes could better determine whether CMFM has been misspecified or CMV may not be detected due to lack of power. Bayesian estimation of CMFM has hardly any convergence problem and best priors may be determined by comparing Deviance Information Criterion (DIC).
Keywords: Common Method Variance, Model Misspecification, Statistical Control, Bayesian Estimation, Monte Carlo Simulation
Abbreviations: CMV: Common Method Variance; DIC: Deviance Information Criterion; EFA Exploratory Factor; CMFM: Analysis Common Method Factor Modeling; BIC: Bayesian Information Criteria; GLM: General Linear Model; WLSMV: Weighted Least Squares Estimator With Chi- Square And Degrees Of Freedom Adjusted For Means And Variances; IG: Inverse Gama
Introduction
Common Or Shared Method Variance (CMV) can stem from a monomethod measurement of both the exogenous and endogenous variables Campbell & Fiske [1]. The literature documents controversies on CMV's effects on relations of substantive constructs. One argument is that CMV is endemic in monomethod measurement and inflates estimates of causal relations to varying degrees Dotty & Glick [2,3], as has been found across multiple disciplines Cote & Buckley [4]. As a result, research findings that relied on monomethod measurement, especially self-reports Chan [5], could be discredited to some extent for possible CMV effects (Brannick, et al.; Chang; Witteloostuijn; Pace [6-8] The counter argument is that CMV is an "exaggerated urban legend" Spector [9]. It is not the shared method per se but other sources of biases that may distort the relations of substantive constructs. In support of this view, CMV has been detected in only a small number of studies in which it could be verified with multimethod measurement Spector; Spector & Brannick [10,11]. Because the presence and degree of CMV is generally unknown in empirical data collected with monomethod measurement, and in light of the ongoing controversies regarding CMV's effects, critical questions arise concerning how to detect CMV's presence and control for its confounding effect. The current study aims to explore the possibility to power analysis through simulation to detect CMV and CMFM with Bayesian estimations to control CMV. The paper is organized as follows. We begin with a brief review of possible sources of CMV and non-statistical controls, then describe relevant issues of statistical control, and demonstrate power analysis to detect CMV and Bayesian estimation as a more effective statistical control.
CMV Sources and Procedural Control
CMV may come from various potential sources, which make procedural controls difficult. Identified sources include rater effects (e.g., social desirability in self-reports, rater bias), item characteristic effects (e.g., ambiguity of content, common format), context of items (e.g., priming effects, item-induced mood, scale length), and context of measurement (e.g., temporal and spatial proximity of both the exogenous and endogenous variables; Podsakoff, Mackenzie, Lee, & Podsakoff [12]. Essentially, CMV represents certain systematic contaminants of the measurements that may be linked to any identified source, although not necessarily to a particular method Lance, Baranick, Lau, Scharlau [13]. Procedural control is generally used to prevent a known contaminant from affecting the measurement process through a deliberate design of the measurement setting and instruments. The multitude of potential sources of CMV and unpredictability of any specific source may hinder procedural controls prior to and during the course of measurement. Statistical control thus becomes useful when a proposed substantive model is thought to be affected by a source of CMV that has not been procedurally controlled.
Statistical Control
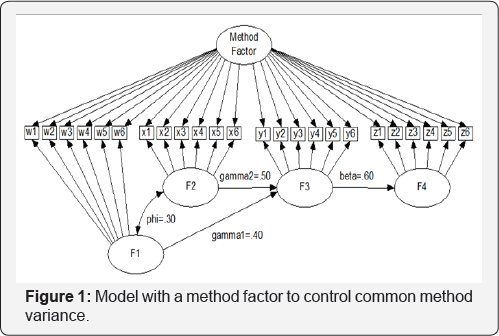
Statistical control is accomplished by incorporating a covariate or specifying a method factor in a model to partition out CMV. The covariate is expected to be theoretically unrelated to the substantive constructs Lindell & Whitne [14], and also "capturing or tapping into one or more of the sources of bias that can occur in the measurement context for substantive variables being examined, given a model of the survey response process" (Williams, Hartman, Cavazotte [15]. When the source of CMV is unknown, a method factor may be specified as measured by indicators of both the exogenous and endogenous substantive constructs (Figure 1). This method factor is not correlated with any other observed or latent variables (orthogonal). This approach has been referred to as unmeasured latent method factor modeling Podsakoff, et al. [12].
ULMF may be taken as a special case of multitrait- multimethod measurement that involves only one method Eid, Nussbeck, et al. [16]. The notion of specifying a latent factor to extract a common variance from different measures also can be seen in a trait-state-error model, in which a trait factor is reflected by indicators of a state factor over time Kenny, Zautra [17], and in a trait-state-occasion model where a trait factor is reflected by the state factors Cole, Martin, Steiger [18]. Conceptually, ULMF appears to be a feasible approach.
CMV may stem from a known source like social desirability, a latent factor that can be measured with its own indicators. Such a latent factor can affect the measurement of both the exogenous and endogenous substantive constructs (Figure 2), causing some CMV. Specifying a model like this to control CMV has been referred to as measured latent method factor modeling Podsakoff, et al. [12] and used in a number of studies Richardson, Simmering, Sturman [19]; Williams, et al. [10]. In the remainder of this article, the ULMF and MLMF are referred to as Common Method Factor Modeling (CMFM), a term attributable to Lindell [14]. (Figures 1 & 2)
Unresolved Issues of Statistical Control
A number of problems exist in the application and performance of statistical control with CMFM. One issue involves imposing equality constraints on the method factor loadings, resulting in equal effects of CMV Williams, Anderson [20]. This practice is based on the assumption that the source of CMV has equal effects on both the exogenous and endogenous constructs Lindell & Whitney [14]. Theoretical justifications for weighting CMV effects equally can be traced back to two statistical theorems. Wainer [21] showed that an equally weighted composite score was as robust as unequally weighted scores in predicting a criterion variable, which appears to be true under limited conditions Raju, Bilgic, Edwards, Fleer [22]; Yang, Nay, Hoyle [23]. The other theorem showed that equal weighting did not affect rankings of individual products (Ree, Carretta, Earles [24]. These theorems might not strictly apply to statistical control of CMV because equal weighting is intended neither to create a composite measure for prediction nor to rank individuals for selection. Nevertheless, the practical advantage of imposing equality constraints on CMV effects is to eliminate the problem of under-identification. In contrast, a congeneric model perspective does not impose equality constraints, allowing the effects of CMV to vary with raters, items, constructs, and contexts (Richardson, et al., 2009). This perspective has been adopted in some studies (Rafferty & Griffin [25]; Williams & Anderson [21]; Williams, et al. [15]. Indeed, without any underidentification problem, imposing equality constraints implies essentially tau-equivalent measurement of the method factor and may be unnecessarily restrictive for a model with multiple indicators of each substantive construct. In general, both equal and congeneric effects of CMV appear to be possible in empirical data. It is unknown which perspective best reflects the model of a particular empirical dataset. If the common method factor does have differential effects, the extent to which imposing equality constraints biases the model parameter estimates is unknown Lindell, Whitney [14].
The second issue involves the efficacy of the statistical control through CMFM. CMFM is rooted in Exploratory Factor Analysis (EFA) in which a model of a single method factor reflected by all the items is typically compared with a multiple- substantive-factors model using the Harman's Single Factor Test Podsakoff, Organ [26]. This test has been used to compare a single factor structure to a multiple factors structure in terms of the total variance explained. It has been evaluated as insensitive when CMV is small Kemery, Dunlap [27], Podsakoff, Todor [28]. Alternatively, the purported method effect might reflect the true covariance between the exogenous and endogenous constructs Podsakoff, et al. [12]. Derived from an EFA, the CMFM approach is occasionally equated to the EFA approach and thus viewed as unreliable Malhotra, Kim, Patil [29]. Such a critique warrants further examination, as the SEM approach differs from its prototype (EFA) and is expected to capture existing CMV like other parameters. However, capturing a small CMV requires that the model is correctly specified and the sample size is large enough for sufficient power. Thus, another question arises concerning how to determine whether the method factor is correctly specified and if power is sufficient to identify the CMV parameter.
Previous findings regarding the performance of CMFM have not been promising. A recent simulation study found that CMFM with an explicit CMV source factor and its own indicators performed slightly better than CMFM with a method factor measured by all the indicators of the substantive constructs Richardson, et al. [19]. However, neither of the two generally performed well in detecting and correcting CMV. As the results were reported in terms of average percentages of correctly and incorrectly detecting CMV (70% and 21%), it is not clear what to expect from CFMF with respect to model convergence, fit, and bias magnitude in parameters of different models under additional unexplored data conditions.
The third issue involves model comparisons for detecting the presence of CMV. Comparing models respectively without and with the method factor has been the standard way to detect the existence of CMV. This standard way is infeasible in some situations. In particular, CMFM can be misspecified for the data that are not contaminated by a CMV source. Given that identification conditions are met, CMFM can still have one of three undesired outcomes: non-convergence, convergence with improper solutions (unreasonable parameter estimates), or false identifications of CMV. When non convergence occurs, it is impossible to proceed with model comparison. Non convergence, however, has not been demonstrated to be a convincing indication of absent CMV in the empirical data, as remains to be confirmed.
Model comparison with a chi-square difference test, however, is not without its own issues. It has been found to be highly sensitive to minor model differences with large sample sizes (Meade, Lautenschlager [30]) and could be affected by the strengths of parameters other than CMV Saris, Satorra, van der Veld [31]. Small misspecification at a large sample size may be detected, while large misspecification at a small sample size may be undetected Kaplan [32]. In addition, misspecifications are more likely to be detected with a chi-square difference test when measurements have low reliabilities as compared to higher reliabilities Miles, Shevlin [33]. As alternatives to avoid these issues, the difference in Akaike Information Criteria (AIC) between two models has been posed where AICdif = x21 - x22- 2 (df1 - df2). Here, x21andx22 are respectively the chi-square fit indices of the two models and df1 and df2 are the corresponding degrees of freedom Kaplan [34]. In addition, the difference in the Bayesian Information Criteria (BIC) or the Adjusted BIC (ABIC) between the two models may also be used for model comparisons. A substantial difference between two models is indicated by a BIC difference above 6 Raftery [35] or an ABIC difference above 4 Akaike [36]. The application of AIC, BIC, ABIC differences, however, are limited to maximum likelihood estimation with continuous data. Model comparisons based on other estimators involve other computations Muthén [37]; Satorra, Bentler [38]. It is unclear if these information criteria differences perform better than a chi-square difference test in identifying the true model, particularly with a large sample size. As model comparison may be impossible due to nonconvergence of a misspecified CMFM, and various difference tests are not definitively indicative of an appropriate CMFM in some situations, certain additional procedures are needed to ensure that CMFM is worth pursuing in empirical data analysis.
Detection of CMV Through Power Analysis
Power analysis through simulations may facilitate detecting misspecification of CMFM. Without sufficient power, small CMV may not be detected even in a correctly specified CMFM of a particular dataset Kaplan [34], Saris, et al. [31]. Simulation is typically conducted by generating random datasets from a population model with known parameters, then fitting the model to these datasets using different estimation methods to evaluate the performance of each estimator in recovering the original population model parameters. Power analysis through simulation is accomplished by assessing the probability that the model can recapture the original parameters at the same sample size with the same estimation methods Muthén [37]. To apply power analysis, given that a sample has been selected from a population with suspected CMV, two models can be used to fit the data: Model H0 without the method factor and Model H1 with the method factor. Two outcomes may be expected when H0 and H1 are fit to the data. First, if H0 is the true model, H1 would be misspecified and would result in a high probability of nonconvergence, or in biased estimates in the converged models. Second, if the H1 model with CMV controlled (namely, CMFM) is the true model of a population, refitting H1 to the randomly generated datasets would result in higher rates of convergence and available power estimates Hancock [39]; Muthén, Muthén [37]. Subsequently, sample sizes can be altered to observe resulting changes in the power of all parameters. As sample sizes increases to be more representative of the population, the power of CMV can also be expected to increase. For a parameter with its population value equal to zero, the power estimate becomes the estimate of Type I error Muthén [37]. Estimating the power of models without and with the method factor using varied sample sizes, the true model thus might be more consistently identified. In addition, issues concerning model comparisons of a specific empirical dataset might be solved, including fit sensitivity to sample size and non-convergence due to misspecification¬.
Bayesian Estimation of CMFM
Within the Bayesian paradigm, each parameter of a model is viewed as a random variable with a certain distribution rather than as a constant in frequentist statistics van de Schoot, et al. [40]. Bayesian estimation has some advantages in modeling small CMV in small samples where the power to detect CMV can be low. First, it does not require large sample theory for the estimation and thus can adapt more readily to small samples Muthén, Asparouhov [41], which are likely to cause non-convergence or biased estimates with ML estimation. Second, Bayesian analysis can allow an analyst to specify known or hypothesized CMV prior distributions in order to observe how the causal relations might vary accordingly. In particular, true CMV values in empirical datasets are typically unknown, and therefore researchers can specify multiple possible priors and observe the change of DIC. As CMV has been found to range from none to 41 in several disciplines Cote, Buckley [4]; Spector [9], thus one may vary the priors accordingly. The best model from different priors can be selected with the smallest DIC. Although varied specifications of reasonable CMV priors may result in slightly different posterior parameter estimates of the focal relations Seaman III, Seaman Jr, Stamey [42], the posterior estimates may not change substantially because they also depend on the likelihood of the parameters for the specific dataset under scrutiny Kamary, Robert [43]. This study thus was also designed to explore the advantages of Bayesian estimation of CMFM, particularly when CMV is unknown in small samples.
Hypotheses
We first hypothesized that the performance of CMFM could be affected by misspecifying the method factor, imposing equality constraints on the method factor loadings, varying the reliability of measurement, and considering small sample sizes. The performance is defined as model convergence and biases in the model parameters, which are examined at different levels of the above factors, including source of CMV (none, unknown, or known), magnitude of CMV (none, small, medium, or large), reliability of measurement (low or high), sample size (small, medium, or large), and treatment of method factor loadings (freely estimate or impose equality constraints). Second, power analysis through simulating large sample sizes could facilitate detecting a misspecification of CMFM, as it relates to convergence rates, Type I errors, and power of the CMV parameter. Third, model comparison was not a viable approach to determine the presence of CMV. Last, Bayesian estimation of CMFM with hypothetical priors had much higher convergence rates and good representations of the population parameters.
We sought first to complement previous studies by adopting models with multiple latent constructs and multiple indicators and simulations to detect potential misspecification of CMV. The simulation data were generated from explicit models with all known parameters, including structural path parameters, factor loadings, and latent variable variances. A congeneric perspective of CMV effects was adopted so that the method factor loadings varied for the substantive constructs in the population models. Second, we sought to demonstrate the advantages of power analysis to detect CMV in empirical data and Bayesian estimation with a few priors.
Method
The three simulation studies were conducted to address the issues mentioned above, as are described below.
Study 1: Hypothetical Population Models and Simulated Data
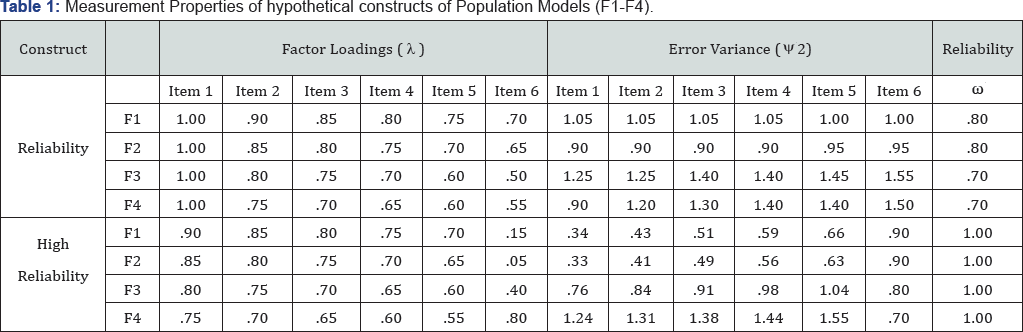
Three hypothetical population models were specified for simulations. The first one was intended to examine the performance of CMFM when CMV is present in the data. Except for the method factor, this model was similar to Figure 1 and had two exogenous constructs (F1 and F2), a mediator (F3), and an endogenous construct (F4). This model was chosen to incorporate more than one exogenous construct (Muthén, 1984) and a mediating effect, whose components are commonly encountered in complicated models in the social sciences and have been advocated for simulation studies by Paxton, Curran, Bollen, Kirby, & Chen (2001). Each construct was set to have six indicators Yang, et al. [23] that are not affected by CMV (w1- w6 for F1, x1-x6 for F2, y1-y6 for F3, and z1-z6 for F4). Factor loadings (λ), residual variances (Ψ2) of the indicators, and reliability (ω) of indicators of each construct were specified based on their relations: ω = (Σλ)2 / [(Σλ)2 + ΣΨ2 ], where (Σλ)2 stands for the square of the sum of factor loadings and ΣΨ2 represents the sum of unique variances McDonald [44]. Omega is the reliability of a scale formed as the unit- weighted composite of the indicators. Reliability, defined as m throughout this report, provides another perspective to examine the measurement quality of the constructs of the simulations. The structural parameters are embedded in Figure 1 with phi = ø = .30, gamma1 = γ 1 = .40, gamma2 = γ 2 = .50, and beta = β = .60. Other parameters were specified to be equivalent to those commonly seen in empirical studies and are listed in Table 1, including factor loadings, errors variances, and reliabilities of indicators. Variances of F1 and F2 and residual variances of F3 and F4 were set at 1.0, 1.0, .60, and .40, respectively. Factor loadings of the method factor were estimated without and with equality constraints (Table 1).
The second population model was intended to examine the performance of CMFM when CMV is present in the data. This model (Figure 1) was extended from the first population model with the inclusion of an additional method factor (F5) measured by all the indicators of the substantive constructs. CMV was respectively set at .20, .33, and .50 to reflect the range of standardized CMV (.20~.50) identified in a previous study (Cote & Buckley, 1987). Factor loadings of the method factor were also estimated without and with equality constraints.

The third population model allowed us to examine the performance of CMFM when CMV has a known source. This model included six hypothetically known indicators of the method factor (v1-v6; Figure 2). The method factor loadings (1.00, .90, .85, .80, .75, and .70) and error variances (1.05, 1.05, 1.05, 1.05, 1.00 and 1.00) were set such that the reliability of the measurement was .80. Variance of this method factor was also respectively set at .20, .33, and .50. Although these known method factor loadings were freely estimated, factor loadings on the hypothetical substantive constructs (F1-F4) were estimated respectively without and with equality constraints.
Three sample sizes were chosen for random data generated from the population models (n = 300, 1200, and 5000). These sample sizes were arbitrarily chosen to represent small, moderate, and large sample size (for sufficient power) because optimal sample sizes that warrant sufficient power for model parameters also depend on distributions, missing data, reliability, and relations among variables. A large number of replications (N=1000) was chosen for each condition simulated in this study Bandalos [45].
Simulations of this study were carried out first by generating data from the three population models according to the specified conditions and then fitting a correct or misspecified model to these datasets. For datasets generated from the first population model without CMV, the misspecified models had a method factor with its loadings estimated respectively without and with equality constraints. For datasets generated from the second and third population models with CMV, the models that were fit back to these data had method factor loadings estimated without or with equality constraints. These data generating and model fitting processes were repeated for each of the three sample sizes, three levels of CMV, and two levels of reliability. The random data generation seed was altered to ensure that different datasets were produced for each condition of the study Paxton, et al. [46]. The method factor was not allowed to be correlated with F1-F4 in any of the processes.
All three simulations were carried out using the latent variable modeling program Mplus, which allows one to specify the population model, generate data, and fit a model to the data. The output also yields power associated with parameter estimates, which are interpreted as power when the true parameters are not zeros, but as Type I errors when the true parameters are zeros.
Average parameter estimates of converged models were compared with the population parameters under all conditions mentioned above. Bias in this study was defined as the difference from the true parameter, as opposed to the percentage bias ((estimate-population) / population), which can be affected by the magnitude of the population parameter. To examine the performance of CMFM under all of these conditions, a preliminary multivariate General Linear Model (GLM) was applied to these pooled estimates, with average biases in the five structural parameters as the dependent variables and two treatments of method factor loadings, sample sizes, reliabilities of measurement, and CMV as independent factors. The GLM was first applied to parameter biases weighted by the inverse variances of the corresponding parameter estimates to account for the use of summary data Marín-Martínez, Sánche-Meca [47]. Slight differences were found in multi-way interactions of these experimental factors, as compared with using the unweighted biases in the parameters as the dependent variables. As it is difficult to interpret these trivial but significant multi-way interactions, biases in parameters without any weighting were subjected to the GLM. The results and further post hoc analyses are described in the next section, with effect size designated as ES. The powers of CMV were also examined with a univariate GLM, but only estimates of data in Tables 2 & 3 with known CMV in the population were examined.
Study 2: Applications of Findings to Empirical Data Modeling
An empirical dataset was obtained from the longitudinal Fast Track project, which is a multisite, multicomponent preventive intervention for children at high risk for long-term antisocial behavior. Descriptions of this project can be found at http://sanford.duke.edu/centers/child/fasttrack/index. html. A normative sample (N=743) was selected for variables used in this study. Two exogenous constructs were selected: parental involvement and volunteering when the child was in grade 6. Two mediating constructs were included: mother-child communication and mother's monitoring of child's negative peer influence when the child was in grade 8. Child delinquency in grade 11 was selected as the endogenous variable. The causal mechanism was assumed as follows: Mother's involvement and volunteering at school at an earlier grade would sensitize and sustain their attentiveness to their children's school performances, and would thereby affect later parental-child communication. Good parent-child communication would help children learn social rules, values, and knowledge and help mothers stay informed about their child's social and academic activities in and out of schools. Related to this communication process is mother's monitoring and buffering of negative peer influences. The communication and monitoring have been theorized to reduce adolescent delinquency Nash, McQueen, Bray [48].
Exogenous Constructs at grade 6: Empirical Constructs were measured with the following scales. Maternal involvement and volunteering at school were measured using the self-rated frequency of the following ten behaviors (with standardized factor loadings in parentheses): stopped to talk to teacher (.57), invited to school for special event (.75), visited school on special event (.83), attended parent-teacher conference(.61), attended Parent-Teacher Association meetings (.72), sent things to class (e.g., books) (.54), read to your child (.40), took child to library (.50), played games at home with child (.25), and volunteered at child's school (.58). The scale had five rating categories (0 = no involvement and4 = high) and a reliability of .84.
Mediating constructs at grade 8 Parent-child communication was measured using mother’s-rating of the following six behaviors with standardized factor loadings in parentheses: discussed beliefs without embarrassment (.60), parent was satisfied with communication (.72), discussed child problems with child (.52), told child how parent really felt (.67), encouraged child to form own opinion (.58), and achieved solutions in problem discussions (.81). The scale had five rating categories (1 = almost never... 5 = almost always) and a reliability of .82.
Parental concern of child negative peer influence was measured with mother’s rating on how often their child’s three friends did the following: got into trouble with police, did things parent disapproved of, and was concerned about negative influence. Standardized factor loadings of the three items were .90, .93, and .92 for the best friend; .89, .91, and .90 for the second best friend; and .92, .93, and .92 for a third best friend. This scale had four rating categories (1= very much and 4 = not at all) and reliabilities of .94, .93, and .95 respectively for each friend.
Outcome constructs at Grade 11 Child delinquency at grade 11 was measured using mother's rating of how often the target child did the following eleven behaviors with standardized factor loadings in parentheses: drank alcohol beyond a few sips (.75), has been drunk in a public place (.88), used illegal drugs such as heroin, crack, cocaine, or LSD (Lysergic acid diethylamide; .72), sold illegal drugs (.84), stolen or tried to steal something worth more than $50 (.76), attacked someone with a weapon with the idea of seriously hurting them (.78), taken some money at home that did not belong to them without asking (.52), been suspended or expelled for bad behavior at school (.66), been in trouble with the police for something he or she did (.81), run away from home (.71), and carried a weapon (.71). This scale had three rating categories (from 0= not true to 2 = very true) and a reliability of .93.
CMV could be suspected due to monomethod measurement of these constructs (the mother’s report or rating). It would be especially helpful to address concerns about CMV in the empirical data. However, a CMV effect might not be found due to temporal separation between the three measurement periods and nonoverlapping items. To test the presence of CMV, a common method factor measured by indicators of the four substantive constructs was specified in the model. Factor loadings of this method factor were estimated respectively without and with equality constraints.
The empirical data were modeled in the following steps. First, the hypothetical model was estimated without a method factor, which served as a reference model. Next, the model was specified to have a method factor reflected by all indicators of the four substantive factors, and estimated without and with equality constraints on method factor loadings. The latter two models were compared with the reference model through a chi-square difference test based on Weighted Least Squares Estimator with Chi-Square and Degrees Of Freedom Adjusted for Means and Variances (WLSMV). This estimator was found to perform relatively well with categorical indicators at various sample sizes Beauducel, Herzberg [49]. Following these steps, each model was simulated to estimate powers of the parameters at the original and doubled sample sizes.
Model Comparisons
Chi-square difference tests and information criteria comparisons were conducted to distinguish the true model (with freely estimated method factor loadings) from a misspecified one (with equality constraints imposed on method factor loadings). Data conditions were chosen such that the smallest CMV stemmed from a known construct with indicators at the largest sample size and lower reliability. This is a situation where a chi- square difference test is expected to perform sensitively and can be meaningfully compared with AIC, BIC, and ABIC differences. Model comparison was conducted only third population (Figure 2) and the model for empirical data.
Study 3: Bayesian Estimation of CMFM with Small Samples:
For the simulation with Bayesian estimation, the two population models (without and with a method factor, see Figure 1) were used to generate one thousand continuous datasets of sample size (n = 150), respectively. CMV for the second population model (Figure 1) was specified at a magnitude of .20. The CMFM was estimated respectively without informative prior distributions of the parameters, with informative priors on the factor loadings, structural parameters, variances and covariance on the two exogenous constructs (F1 and F2).
Prior distributions for the model were specified as follows. Priors for the factor loadings and structural regression parameters were specified as normally distributed with their means equal to the population model parameters and a variance 30 for each. The variance ofthe method factor has an Inverse Gama (IG) distribution with two positive parameters that respectively defines the shape (α) and scale (β) of the probability density function. The expected mean and variance of this distribution are respectively 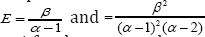 with restrictions that α is greater than 1 for the mean and greater than 2 for the variance. To translate a prior CMV information into α and β parameters of an IG distribution, we can rearrange the above equations, so that
with restrictions that α is greater than 1 for the mean and greater than 2 for the variance. To translate a prior CMV information into α and β parameters of an IG distribution, we can rearrange the above equations, so that 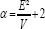 , as suggested by Cowles [50]. For instance, if a small prior of mean E = .10 and variance V = .20, then the shape parameter α = 2.05 and scale parameter β = .10; If a moderate prior of mean E = .30 and variance V = .30, then the shape parameter α = 2.30 and scale parameter β = .39. The variance and covariance of F1 and F2 has an Inverse Wishart distribution - IW (sigma, df ), where , sigma = v * (2p + 2) v = known or expected variance or covariance, p = the number of variables of variance and covariance matrix of sigma, and df = p + 2 . More details on translating certain variances and covariances into IW priors have been described by Muthén & Asparouhov [41] and discussed on http://www.statmodel. com/discussion/messages/9/6256.html#POST111957. Priors for the error variances were not specified, but relied on the ML estimates.
, as suggested by Cowles [50]. For instance, if a small prior of mean E = .10 and variance V = .20, then the shape parameter α = 2.05 and scale parameter β = .10; If a moderate prior of mean E = .30 and variance V = .30, then the shape parameter α = 2.30 and scale parameter β = .39. The variance and covariance of F1 and F2 has an Inverse Wishart distribution - IW (sigma, df ), where , sigma = v * (2p + 2) v = known or expected variance or covariance, p = the number of variables of variance and covariance matrix of sigma, and df = p + 2 . More details on translating certain variances and covariances into IW priors have been described by Muthén & Asparouhov [41] and discussed on http://www.statmodel. com/discussion/messages/9/6256.html#POST111957. Priors for the error variances were not specified, but relied on the ML estimates.
Results
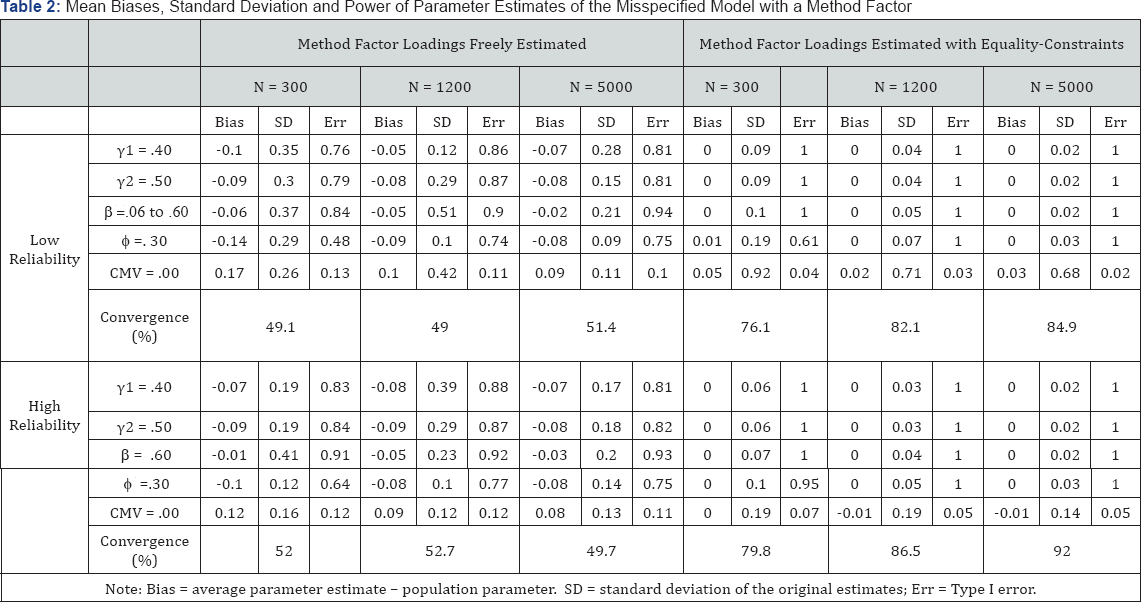
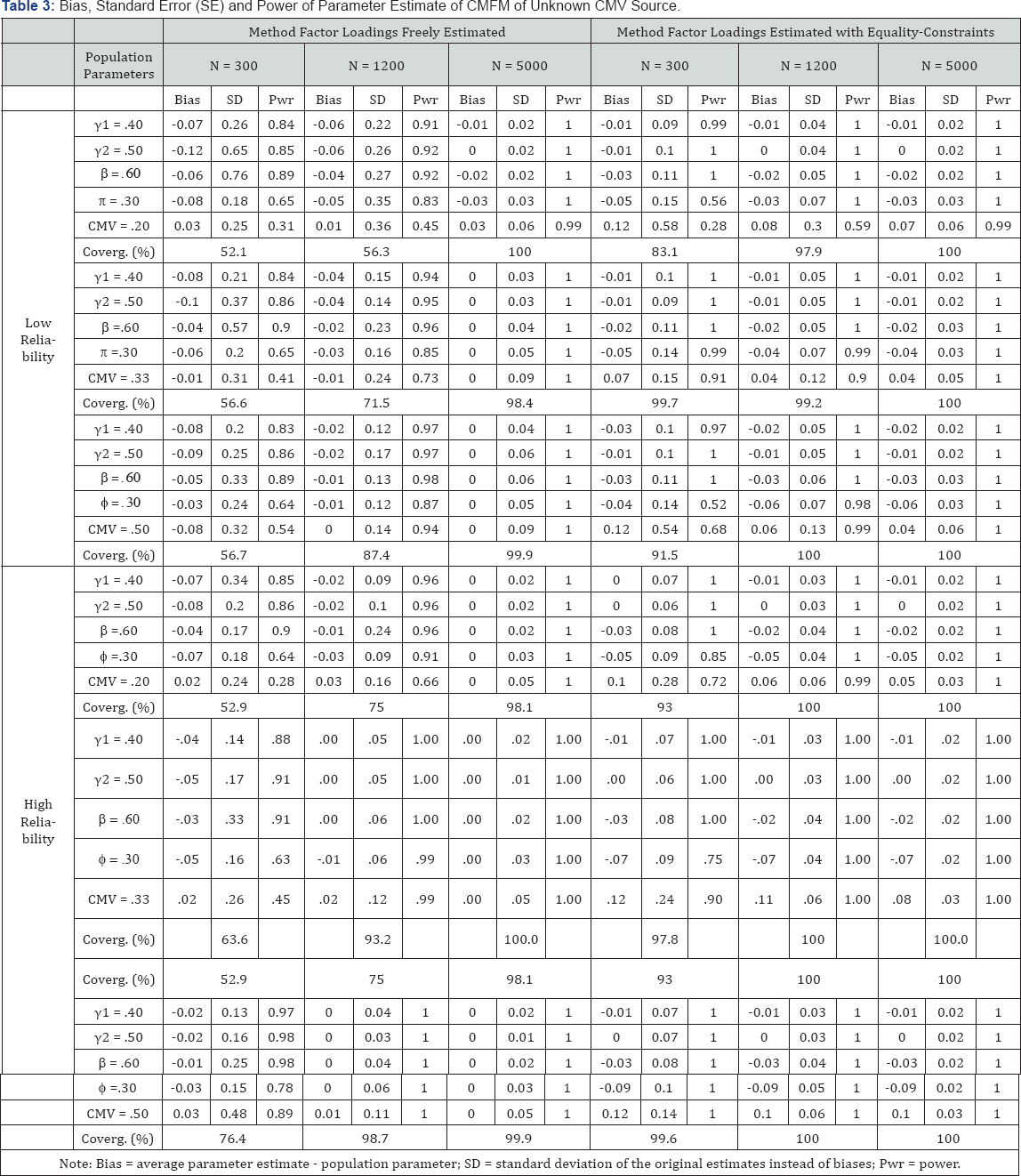
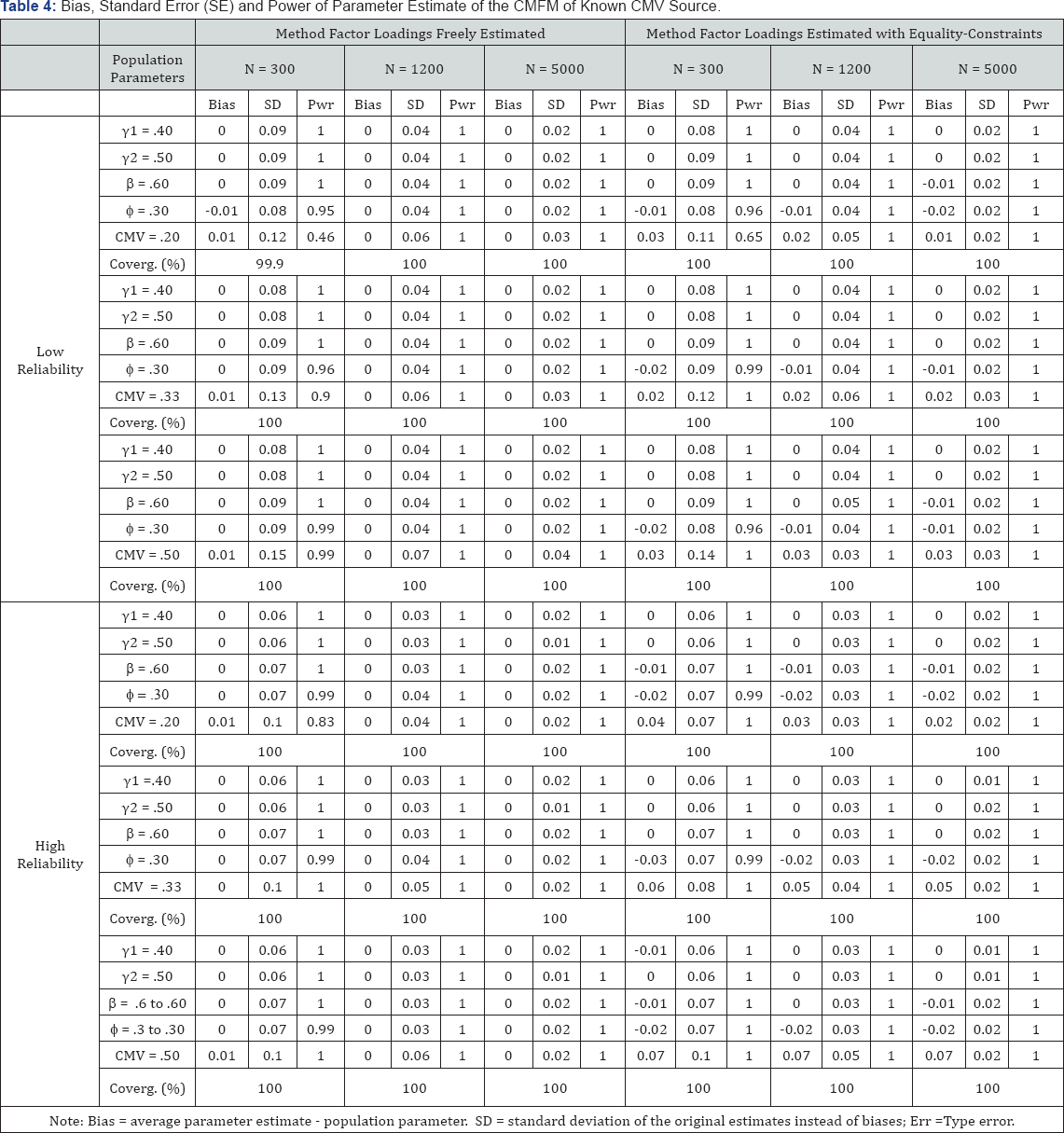
The results of the study include the following five parts: first, performance of CMFM under specific conditions; second, biases in the structural parameters; third, power analysis of CMFM; fourth, CMFM of empirical data; and fifth, Bayesian Estimates of the CMFM. Biases in five structural parameters ( γ 1, γ 2, β, ø, and CMV), standard deviations of the estimates under each condition, and powers of the main structural parameters and percentage of convergence for the simulated models are listed in Table 2-4.
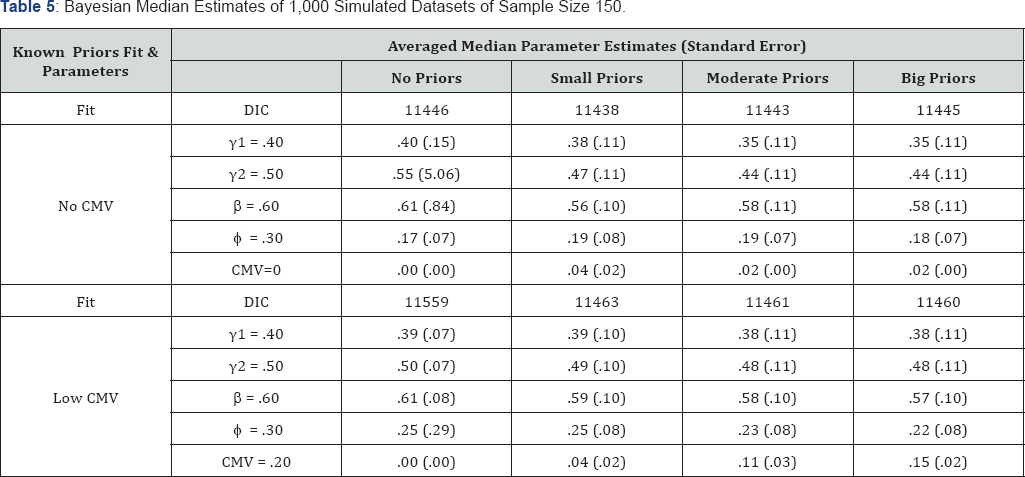
Bayesian estimates are listed in Table 5.
Performance of CMFM under Non-existent CMV
Table 2 (left half) shows two patterns emerged from the simulations when the CMFM with method factor loadings freely estimated was misspecified for dataset generated from a model without CMV. First, as shown by the convergence rates, about 50% of the models did not converge to yield any parameter estimates. Second, biases in the parameters revealed that converged models overestimated CMV but underestimated other structural parameters. Table 2 (right half) also shows that imposing equality constraints on the method factor loadings increased model convergence rates but underestimated Type I errors of CMV, leading to greater chances of falsely identifying CMV. Specifically, in the absence of CMV, there were higher chances of model convergence (76.1% ~ 92.0%) when method factor loadings were constrained to be equal than when they were freely estimated (49.0% ~ 52.7%), as indicated by a two- sample proportion test (z = 12.99 ~ 23.51, p < .01). Although larger biases in CMV were found in the former condition (range = .11~ .17) than in the latter condition (range = -.01~.05; z = 2.56 ~ 12.35, p < .05). Type I errors below .05 implied the absence of CMV.
Performance of CMFM under Three Levels of CMV with Unknown Source
In the presence of CMV from an unknown source, convergence rates (see Table 3) were also lower at small or moderate sample sizes when method factor loadings were freely estimated (52.1% ~ 98.7%) than when they were estimating with equality constraints (83.1% ~ 100%; z = 3.63 ~ 27.33, p < .01). Biases in the CMV were also smaller under the former condition (range = - .08 ~ .03) than under the latter condition (range=.04 ~ .12; z = 3.90 ~ 54.21, p < .01).
Performance of CMFM under Three Levels of CMV with Known Source
When CMV from a known source was present, a similar pattern of results emerged (see Table 4). Biases in the CMV were small but also significant between the two treatments of method factor loadings (range = .00 ~ .07; z = 1.79 ~ 78.26, p < .06). Over 99.9% of the models converged under both conditions. When the method factor loadings were allowed to be freely estimated and the power of CMV was over. 45, average biases in the focal structural parameters were under. 10.
Overall Biases in Other Structural Parameters of CMFM
The multivariate GLM of pooled estimates revealed that different treatment of the method factor loadings had the strongest effects on biases in the structural parameter (γ 1, γ 2, β, ø, and CMV) estimates (F(5,58) = 35.58, p < .01, ES = .75). However, these effects also depended on the source of CMV (F(5,58) = 14.03, p < .01, ES = .54), the reliability of measurement (F(5,58) = 4.38, p < .01, ES = .27), the magnitude of CMV (F(10,116) = 2.70, p < .01, ES = .19), and the sample size (F(10,96) = 2.92, p < .01, ES = .20). Other conditions of the studies also contributed to the biases in the structural parameter estimates. These included sample size (F(10,116) = 5.12, p < .01, ES = .31), reliability (F(5,58) = 2.57, p < .01, ES = .18) as main effects, and their interaction with source of CMV (F(20,193) = 3.33, p < .01, ES = .22). Biases were smaller when CMV was known to be caused by a construct with its own indicators (mean =.02) than when CMV source was unknown (mean=.04, F((5,58) = 38.20, p < .01, ES = .77). In sum, different treatments of method factor loadings (constrained or freely estimated) and source of CMV (unknown and known from a measurable construct) affected the overall performance of CMFM heavily, while sample sizes, reliabilities of measurement, and the magnitude of CMV did less severely. These imply the poor performance of CMFM and the difficulty to decide when equality constraints may be robustly imposed on the method factor loadings.
Power Analysis of CMV
When CMV was absent in the true model and method factor loadings were freely estimated, power estimate (Type I errors in this case) of misidentified CMV were above the significance level of .05 (.11 ~ .13) and did not increase with enlarged sample sizes, as can be seen in Table 3. In addition, when equality constraints were imposed on the method factor loadings, the underestimated Type I errors of CMV remained below or close to a significant level of .05, and did not vary with an increase in sample size, either. Therefore, the relative stability of Type I errors, irrespective of sample sizes, can be used as an indication of the absence of CMV.
When CMFM was correctly specified to fit data with CMV, the power for detecting CMV varied with sample sizes. With high power at large sample size (N=5000), biases in focal structural parameters were reduced to zero and standard deviations of these biases became small (ranging from .01 to .09). In contrast, biases in CMV could not be reduced to zero when models were estimated with equality constraints imposed on the method factor loadings. Thus, increasing the power to detect CMV through larger samples can also find slight changes in the precision of parameter estimates.
Model comparisons at large sample sizes with a known CMV source
Model comparisons yielded mixed results. The Chi-square difference tests showed that only .02% of models with freely estimated method factor loadings were identified to be better than the misspecified one with equality constraints imposed on the method factor loadings. AIC difference tests showed that 6l.5% of true models fit the data better than the misspecified model. BIC and ABIC differences showed that 100% and 99% of models with freely estimated method factor loadings fit the data better than misspecified models.
CMFM of Empirical Data and Power Analysis
The baseline model without the common method factor fit the empirical data well (χ 2 (585) = 1241.10, p < .01, CFI = .96, TL1 = .96, RMSEA = .04). Mother's involvement and volunteering at school at an earlier grade was found to predict mother-child communication (β = .23, p < .01) and mother’s monitoring of negative peer influences (β = .13, p < .01). The latter two constructs predicted low delinquency (β = -.16, p < .01 and β = -.47, p < .01), respectively, and explained 29% of the variance in delinquency.
Models with a common method factor yielded different results. The model with method factor loadings freely estimated did not converge. The model with method factor loadings constrained to be equal fit the data well (χ 2 (583) = 1264.41, p < .01, CFI = .96, TLI = .96, RMSEA = .04). This model fit the data slightly worse than the baseline model as indicated by a significant chi-square difference (χ2dif (2) = 23.31, p < .01). Parameter estimates of this model were slightly different from those of the baseline model. Mother’s involvement and volunteering at school at an Bayesian Estimates of CMFM earlier grade predicted mother-child communication (β = .22, p < .01) and mother's monitoring of negative peer influences (3 = .12, p < .01). The latter two constructs predicted less adolescent delinquency (β = -.19, p < .01 and β = -.50, p < .01, respectively). A small nonsignificant CMV was identified by this model (CMV =.02, p = .65). This model explained slightly more of the variance in delinquency (33%) than did the baseline model. Simulations of 1000 samples at the original sample size showed that CMV had a mean of .04, a standard deviation of .16, and a power or Type I error smaller than < .001. Doubling the sample size resulted in a mean of .04, a standard deviation of .13, a power or Type I error of .001 for the CMV. In addition, the minimum power of other structural parameters was .76 at the original sample size and .97 at the doubled sample size. This finding was consistent with the slight over-estimation of CMV with equality constraints on the method factor loadings, and thus the non-existence of CMV in the data could be inferred.
Bayesian Estimates of CMFM
Note: DIC: Deviance Information Criterion.
The CMFM population parameters, DIC, and posterior estimates derived from four CMV priors are listed in Table 5. Although not reported in this Table, the lowest convergence rate was 97.6% under each condition. The parameter estimates were the means of the median point estimates obtained from one thousand simulated datasets. The median estimates were chosen for the report over the mean estimates because the posterior estimates might not be normally distributed for the mean estimates to be more meaningful. The numbers in Table 5 suggest the following. The smallest DIC (bold) indicate which prior specifications led to the optimal posterior estimates. When CMV was not present in the population model, a small prior for CMV enabled the model to fit the data better than other possible priors. When CMV was present in the data, the CMV parameter could be best recovered with a prior close to the population parameter, as indicated by both the smallest DIC and its mean median estimate.
Discussion
The three simulation studies of this report have showed the problems of CMFM in detecting and controlling CMV under limited data conditions, and demonstrated the advantages of power analysis to detect CMV and Bayesian estimation of CMFM to control for CMV. To make the findings more generalizable than a simple measurement model, the CMFM of this study was designed to include two exogenous constructs and a mediating construct. Given these limited conditions and the unavailability of a universal model, we obtained the following findings. First, in the absence of CMV, misspecified CMFM models had about a 50% chance of non-convergence. Converged but misspecified models overestimated CMV and underestimated other structural parameters. When sample sizes or CMV were small, even correctly specified CMFM had similar chances of non-convergence. These findings confirmed the overall low success rate of CMFM in identifying CMV (Richardson, et al., 2009). Non-convergence of CMFM under these conditions rendered model comparison impossible and thus failed to permit a test of whether the method factor model should have been specified or not.
Model comparisons under the limited condition of this study were largely consistent with previous findings. Chi- square difference tests were insensitive to the misspecification of equality constraints on the factor loadings at large sample sizes where it was expected to be overly sensitive, if anything. Although the Chi-square difference test indicated that models with equality constraints on the method factor loadings differed significantly from the model without the method factor, it was difficult to correctly infer which model best reflected the population. AIC performed better than the Chi-square difference test but it did not reach 95% probability of identifying the correct model, in terms of a statistical significance. BIC and ABIC differences favored the correctly specified model but are limited to maximum likelihood estimation (ML). For ordinal data, ML requires numeric integration and can be computationally challenging with complex models. In addition, BIC has a limitation of favoring excessively simple models Weakliem [51]. Therefore, in light of these findings and chances of non-convergence, model comparison appears to have limited use for detecting CMV.
Second, power analysis through simulations of large samples was found to identify misspecified CMFM effectively. Simulations of CMFM indicated that Type I errors of the CMV parameter would remain above a significant level and relatively stable if CMV was absent in the true model, while the power of CMV would increase if it was present in the true model. With sufficient power, biases in the structural parameters of our focal interest in this study could also be minimized. These findings were consistent with studies on the detection of model misspecification that show correctly specified models and sufficient power are necessary and complementary conditions for reducing biases associated with CMV Saris, et al. [52].
Third, biases in the parameters depended on the treatment of method factor loadings, the magnitude of CMV, sample sizes, measurement properties of latent constructs, and the knowledge of the CMV source. Imposing equality constraints on the method factor loadings increased the chances of misidentifying CMV, underestimated Type I errors, and overestimated CMV. CMFM performed well when CMV and sample sizes were large and when the model was correctly specified (without equality constraints on the method factor loadings). It performed best when the method factor that caused CMV was measured explicitly with its own indicators, as was also consistent with previous studies.
For the empirical data of this study, power analysis through simulations facilitated choosing a plausible model. The power of CMV with equality constraints on the method loadings remained under .05, even at a doubled sample size. The unchanged power (or type I error) matched findings from the simulations that CMV could have Type I errors close to .05 when CMFM was misspecified for data without CMV. This information suggests that CMV could be inferred to be absent in the empirical data. In addition, no overlap or similarity in contents of indicators for all the constructs or temporal proximity in the measurement were found that might cause CMV. Thus, the suspicion of CMV in the measurement and the model control CMV could be inferred to be unfounded.
Bayesian estimation of the CMFM appears to be promising to control CMV in this study, because it allows an analyst to experiment with unknown prior distributions of the CMV and observe DIC for best model fit. With the best priors specified, the median posterior estimates of the key structural parameters did not deviate much from the true population parameter and remained within the credibility intervals. Biases in the parameters have not been reported in the result, because we think it uninteresting to compare the average medians of 1,000 distributions to the population parameters.
Limitation of this Study
Suspicion of CMV in the measurement requires explicit assumptions and justification for them (Brannick, et al, [6]. The population model for this study has been hypothetically specified to have the method factor measured by all the indicators. Based on explicit assumptions in practice, the method factor may be measured by only some indicators of the exogenous and endogenous latent constructs. Alternatively Eid, Lischetzke [53.54] , covariances of some errors may be allowed to be freely estimated, instead of specifying a method factor Marsh, Grayson [53.55] .
Recommendations for Researchers
First, power analysis with larger sample sizes may be applied to a CMFM to confirm the existence of CMV, if it is suspected based on justifiable assumptions. It may be necessary to impose equation constraints on the method factor loadings ONLY to make the estimation converge in the power analysis. Second, CMFM with Bayesian estimation may be explored with a few prior distributions of CMV to observe the smallest DIC for the best model.
References
- Campbell DT, Fiske DW (1959) Convergent and discriminant validation by the multitrait multimethod matrix. Psychological Bulletin 56(2): 81-105.
- Dotty DH, Glick WH (1998) Common methods bias: Does common methods variance really bias results. Organizational Research Method 1(4): 374-406.
- Williams LJ, Brown BK (l994) Method variance in organizational behavior and human resources research: Effects on correlations path coefficients and hypothesis testing. Organizational Behavior and Human Decision Processes 57(2): 185-209.
- Cote JA, Buckley R (1987) Estimating trait method and error variance: Generalizing across 70 construct validation studies. Journal of Marketing Research 24(3): 315-318.
- Chan D (2009) So why ask me Are self report data really that bad In CE Lance RJ Vandenberg (Eds) Statistical and methodological myths and urban legends: Doctrine verity and fable in the organizational and social sciences New York Routledge : pp. 309-336.
- Brannick MT, Chan D, Conway, JM Lance, Spector PE, et al. (2010) What is method variance and how can we cope with it A panel discussion. Organizational Research Methods 13(3): 407-420.
- Chang SJ, van Witteloostuijn A, Eden L (2010) From the editors: Common method variance in international business research. Journal of International Business Studies 41(2): 178-184.
- Pace VL (2010) Method variance from the perspectives of reviewers: Poorly understood problem or overemphasized complaint. Organizational Research Methods 13(3): 421-434.
- Spector PE (2006) Method variance in organizational research: Truth or urban legend Organizational Research Methods 9(1): 221-232.
- Spector PE (1987) Method variance as an artifact in self reported affect and perceptions at work: Myth or significant problem. Journal of Applied Psychology 72: 438-443.
- Spector PE, Brannick TM (2010) Common method issues: An introduction to the feature topic in organizational research methods. Organizational Research Methods 13(3): 403-406.
- Podsakoff PM, Mackenzie SB, Lee JY, Podsakoff NP (2003) Common method biases in behavioral research: A critical review of the literature and recommended remedies. Journal of Applied Psychology 88(5): 879-903.
- Lance CE, Baranick LE, Lau AR, Scharlau EA (2009) If it aint trait it must be method: (Mis)application of the multitrait multimethod design in organizational research. In CE Lance RJ Vandenberg (Eds) Statistical and methodological myths and urban legends: Doctrine verity and fable in the organizational and social sciences pp309-336 New York, Routledge: pp. 309-336
- Lindell MK, Whitney DJ (2001) Accounting for common method variance in cross sectional research designs. Journal of Applied Psychology 86(1): 114-121.
- Williams LJ, Hartman N, Cavazotte F (2010) Method variance and marker variables: A review and comprehensive CFA marker technique. Organizational Research Methods 13(1): 477-514.
- Eid M, Nussbeck FW, Geiser C, Cole DA, Gollwitzer M, et al. (2008) Structural equation modeling of multitrait multimethod data: Different models for different types of methods. Psychological Methods 13(3): 230-253.
- Kenny DA, Zautra A (1995) The trait state error model for multiwave data. Journal of Consulting and Clinical Psychology. 63(1): 52-59.
- Cole DA, Martin NC, Steiger JH (2005) Empirical and conceptual problems with longitudinal trait state models: Introducing a trait state occasion model. Psychological Methods 10(1): 3-20.
- Richardson HA, Simmering MJ, Sturman MC (2009) A tale of three perspectives: Examining post hoc statistical techniques for detection and correction of common method variance. Organizational Research Methods 12: 762-800.
- Williams LJ, Anderson SE (1994) An alternative approach to method effects by using latent variable models: Applications in organizational behavior research. Journal of Applied Psychology 79(3): 323-331.
- Wainer H (1976) Estimating coefficients in linear models: It dont make no nevermind. Psychological Bulletin 83(2): 213-217.
- Raju NS, Bilgic R, Edwards JE, Fleer PF (1997) Methodology Review: Estimation of population validity and cross validity and the use of equal weights in prediction. Applied Psychological Measurement 21(4): 291-305.
- Yang C, Nay S, Hoyle HR (2010) Three approaches to using lengthy ordinal scales in structural equation models: Parceling latent scoring and shortening scales. Applied Psychological Measurement 34(2): 122-142.
- Ree MJ, Carretta TR, Earles JA (1998) In top-down decisions weighting variables does not matter: A consequence of Wilks theorem. Organizational Research Methods 1(4): 407-420.
- Rafferty AE, Griffin MA (2004) Dimensions of transformational leadership: Conceptual and empirical extensions. Leadership Quarterly 15: 329-354.
- Podsakoff PM, Organ DW (1986) Self reports in organizational research: Problems and prospects. Journal of Management 12: 69-82.
- Kemery ER, Dunlap WP (1986) Partialling factor scores does not control method variance: A rejoinder to Podsakoff and Todor. Journal of Management 12: 525-530.
- Podsakoff PM, Todor WD (1985) Relationships between leader reward and punishment behavior and group processes and productivity. Journal of Management 11: 55-73.
- Malhotra NK, Kim SS, Patil A (2006) Common method variance in IS research: A comparison of alternative approaches and a reanalysis of past research. Management Science 52 (12): 1865-1883.
- Meade AW, Lautenschlager GJ (2004) A Monte Carlo study of confirmatory factor analytic tests of measurement equivalence invariance. Structural Equation Modeling 11(1): 60-72.
- Saris WE, Satorra A, van der Veld WM (2009) Testing structural equation models or detection of misspecifications Structural Equation Modeling 16(4): 561-582.
- Kaplan D (1995) Statistical power in structural equation modeling In RH Hoyle (Ed) Structural equation modeling Concepts issues and applications. Thousand Oaks CA US Sage Publications Inc: pp. 100-117.
- Miles J, Shevlin M (2007) A time and a place for incremental fit indices. Personality and Individual Differences 42: 869-874.
- Kaplan D (2000) Structural equation modeling: Foundations and extensions. Thousand Oaks CA Sage Publications, USA.
- Raftery AE (1995) Bayesian model selection in social research. Sociological Methodology 25: 111-163.
- Akaike H (1980) Likelihood and the Bayes procedure. In JM Bernardo, MH De Groot, DV Lindley AFM Smith (Eds) Bayesian statistics Valencia Spain University Press, Spain, pp. 143-166.
- Muthén LK, Muthén BO (1998-2012). M plus users guide (6th ed) Los Angeles CA: Muthén & Muthén.
- Satorra A, Bentler PM (2010) Ensuring positiveness of the scaled difference chi-square test statistic. Psychometrika 75(2): 243-248.
- Hancock GR (2006) Power analysis in covariance structural modeling. In GR Hancock RO Mueller (Eds) Structural equation modeling: A second course Greenwich Connecticut: Information Age Publishing :pp 69-115.
- van de Schoot R, Kaplan D, Denissen J, Asendorpf JB, Neyer FJ, et al. (2013) A gentle introduction to Bayesian analysis: applications to developmental research. Child Development
- Muthén BO, Asparouhov T (2012) Bayesian structural equation modeling: A more flexible representation of substantive theory.Psychological Methods 17(3): 313-335.
- Seaman JW, Seaman JW, Stamey JD (2012) Hidden dangers of specifying noninformative priors. The American Statistician 66(2): 77-84.
- Kamary K, Robert CP (20l4) Reflecting about selecting non informative priors 3: 175.
- McDonald RP (l999) Test theory: A unified treatment. Mahwah New Jersey Lawrence Erlbaum Associates, USA.
- Bandalos DL (2006) The use of Monte Carlo studies in structural equation modeling research. In GR Hancock RO Mueller (Eds) Structural equation modeling A second course Greenwich Connecticut: Information Age Publishing : pp. 385-426.
- Paxton P, Curran PJ, Bollen KA, Kirby J, Chen F (200l) Monte Carlo experiments: Design and implementation. Structural Equation Modeling 8(2): 287-312.
- Marín Martínez F, Sánche Meca J (2010) Weighting by inverse variance or by sample size in random effects meta-analysis. Educational and Psychological Measurement 70 (1): 56-73.
- Nash SG, McQueen A, Bray JH (2005) Pathways to adolescent alcohol use: Family environment, peer influence and parental expectations. Journal of Adolescent Health 37: 19-28.
- Beauducel A, Herzberg PY (2006) On the performance of maximum likelihood versus means and variance adjusted weighted least squares estimation in CFA. Structural Equation Modeling 13(2): 186-203.
- Cowles MK (20l3) Applied Bayesian statistics: with R and Open BUGS examples. Springer Science & Business Media, Germany
- Weakliem DL (1999) A critique of the Bayesian Information Criterion for model selection. Sociological Methods & Research 27(3): 359-397.
- Saris WE, Satorra A, Sorbom D (l987) Correction of specification errors in structural equation modeling. Sociological Methodology 17(1): 105-129.
- Marsh HW, Grayson D (1995) Latent variable models of multitrait multimethod data. In RH Hoyle (Ed) Structural equation modeling: Concepts issues and applications.Thousand Oaks CA Sage, USA, pp. 177-198.
- Eid M, Lischetzke T, Nussbeck FW, Trierweiler LI (2003) Separating trait effects from trait specific method effects in multitrait multimethod models: A multiple indicator CTC (M-1) model. Psychological Methods 8(1): 38-60.
- Muthén LK, Muthén BO (2002) How to use Monte Carlo study to decide on sample size and determine power. Structural Equation Modeling 9(4): 599-620.






























