Mini Review

Simulation Phase-Structure Transformations in Alloy Steels for The Piersing Tools

Sergiiv Bobyr^1,2,3*, Dr Sc² and Dmitro V Loschkarev³

Applied Sciences Department, University of Technology, Iraq

Submitted: March 21, 2019; Published: April 25, 2019

*Corresponding author: Sergiiv Bobyr, Department of Steel Heat Treatment, Ukraine

How to cite this article: Sergiiv B, Dr Sc, Dmitro V L. Simulation Phase-Structure Transformations in Alloy Steels for The Piersing Tools. JOJ Material Sci. 2019; 5(3): 555665. DOI: 10.19080/JOJMS.2019.05.555665

Abstract

In this work are presented the development of simulation methods of analysis the phase-structural transformations and properties in alloy steels. The analytical dependencies of this simulation were applied to the calculation of ferritic, pearlite and bainitic transformations in carbon and alloy steels. To calculate the amount of martensite, the authors used a new equation that has been successfully used in others works too. Based on the developed regression model, isothermal and structural diagrams for 20CrNi4V and 25Cr2Mo1V steels have been constructed. The analysis is performed of the aerial quenching of tools from alloy steels 20CrNi4V and 25Cr2Mo1V, according to the recommended heat treatment schedules in the tools production. For steels 20CrNi4V and 25Cr2Mo1V, it is possible to obtain a bainitic structure in a wide range of cooling rate. Corrections of heat treatment schedule were proposed.

Keywords: Heat treatment; Phase- structural transformation; Properties; simulation methods; Alloy steel; Piersing tools

Introduction

Improvement of heat treatment process is efficient, if a complete picture is known of the main features and characteristics of processed alloys. Important information is about the kinetics of supercooled austenite transformation, on which the basis issues are addressed of hardenability, heat treatment schedules and the mechanical properties (YTS, UTS, E% and HB).Experimental study of microstructure components in the heat treatment of allow steels consists of the building of time-temperature (TTT) and continuous cooling (CCT) transformation diagrams, as well as in the study of steels hardenability. Modern researches are implemented in the special purpose software packages like JMatPro or ESI Group products for steels modelling. User is able to calculate phase changes for an assigned chemical composition of steel and different modes of treatment, e.g. continuous heating and tempering. That makes it possible to predict the details of the structure after heat treatment [1-3] including large-scale rolls [4-6]. User needs to integrate own routines for calculating diagrams of phase transformations, for example, when heat treatment is combined with cryogenic processing [7]. The aim of this work is development of simulation methods of analysis the phase-structural transformations in alloy steels for the piercing tools.

Analytical Models Phase-Structure Transformations

Analytical model of austenite transformation was applied for the steel structure modelling based on the Analytical model of austenite transformation was applied for the steel structure mod elling based on the results obtained in [7]. The M. Avrami equation was used of the phase transformation kinetics, written in the following form:

where P_α – result of the phase transformation (amount of formed ferrite, pearlite or bainite); V – relative rate of transformation; n – degree of equation; τ – time of transformation (below critical point Ac₃ for the ferrite, Ac₁ for the pearlite and Ac₀ – for bainite).

The relative rate of conversion is given by [8,9]

where ΔT = Tc – T, T – current temperature; Tc – temperature critical points of transformation; Q – the activation energy of carbon diffusion in the alloy steel; K – constant coefficient; R – universal gas constant, 1,987 [cal K⁻¹ mol⁻¹]. Parameter Q for ferrite and pearlite is equal to the activation energy of carbon diffusion in the austenite of steel, and for bainite, it is equal to the activation energy of carbon diffusion in steel ferrite. Temperature Ac0 for roll steels is calculated from the condition that the maximum of the bainite growth rate coincides according to temperature, calculated from equation (2) and its experimental value on an isothermal diagram. This value is 600 °C for steel 25Cr2Mo1V and 580 °C for steel 20CrNi3V.

The steel used for model verification is 25Cr2MoV with known diagrams of austenite transformation and thestructure after treatment. The improved model explicitly contains the rate of phase and structure transformation (ferrite, pearlite, bainite) that allows more clearly to interpret physical coefficients. To describe the process of martensite formation, the model includes both the start and end temperature of transformation.

A technique for Simulation Phase-Structural Transformations in Alloy Steels

Special alloy steels 20CrNi4V and 25Cr2Mo1V are used for the rolling and piercing tool. The chemical compositions of alloy steels are given in (Table 1). The analytical equation of phase transformations was adopted to be applicable in the computer simulation. The algorithm for simulation phase transformations in alloy steels is as follows.

a) Calculation of critical points of phase transformations according to the regression model developed for certain range of chemical compositions of alloy steels.

b) Building of TTT for the calculated critical points.

c) Construction of a CCT by the proposed calculation method.

d) Calculation the cooling curves and the boundaries of phase transformations at surface of tools and their comparison with experimental data.

e) Calculation the number and fractions of microstructure components in the steel at the end of cooling

f) The analytical TTT and CCT diagrams are currently determined for a given range of chemical composition of steels by the statistical processing of the highly alloyed steel grades. That is resulted in a possibility to consider the complete list of alloying elements and enough wide range of their mass fraction. This is the advantage of the developed analytical models in contrast to the experimental methods of the TTT and CCT determination by the dilatometric measurements.

Simulation Phase-Structural Transformations in Alloy Steels

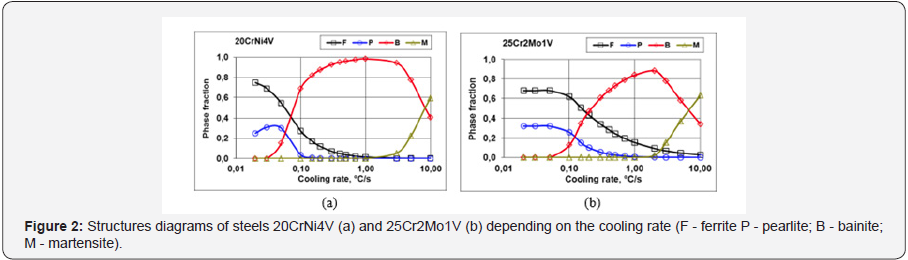
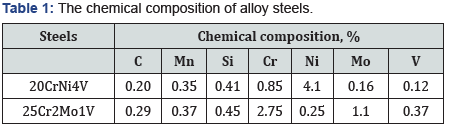
Under isothermal conditions, an alloy steel 20CrNi4V and 25Cr2Mo1V undergoes three austenite transformations: ferritic, pearlitic and bainitic (Figure 1). In steel 20CrNi4V (Figure 1a) there is temperature range of austenite stability between the areas of pearlite and bainite, which formation begins earlier than in 25Cr2Mo1V steel. The region of pearlite transformation is shifted to the right side, which indicates an increased stability of austenite due to alloying elements In alloy steel 25Cr2Mo1V between pearlitic and bainitic areas (Figure 2b) exists of area increased stability of austenite in the temperature near 600 °C. Differences in alloy elements of these steels determine the type of diagrams (Figure 2). The steel structure 20CrNi4V cooled at a rate 0.5°C/s (corre sponds to tools surface cooling) has at 20 °C ferrite (5%) and bainite (92%) and retained austenite (3%). Steel 25Cr2Mo1V cooled at a rate 0.5 °C/s includes at room temperature ferrite (27%), pearlite (3%) and bainite (70%) (Figure 3).

Conclusion

In this work are presented the development of simulation methods of analysis the phase-structural transformations and properties in alloy steels for piersing tools. The analytical dependencies of this simulation were applied to the calculation of ferritic, pearlitic and bainitic transformations in carbon and alloy steels. To calculate the amount of martensite, the authors used a new equation that has been successfully used in others work too. Based on the developed regression model, isothermal and structural diagrams for 20CrNi4V and 25Cr2Mo1V steels have been constructed; their correspondence to experimental data has been established. The analysis is performed of the aerial quenching of tools from alloy steels 20CrNi4V and 25Cr2Mo1V, according to the recommended heat treatment schedules in the tools production. for steels 20CrNi4V and 25Cr2Mo1V, it is possible to obtain a bainitic structure in a wide range of cooling rate. Corrections of heat treatment schedule were proposed.

References

1. Buchmayr B, Kirkaldy JS (1990) Modeling of the temperature field, transformation behavior, hardness and mechanical response of low alloy steels during cooling from the austenite region, Journal of Heat Treating 8(2): 127-136.
2. Simsir C, Gur, CHA (2008) FEM based framework for simulation of thermal treatments: Application to steel quenching, Computational Material Science 44: 588-600.
3. Sugianto A, Narazaki M, Kogawara M, Shirayori A (2009) Numerical simulation and experimental verification of carburising-quenching process of SCr420H steel helical gear, Journal of Material Processing Technology 209(7): 3597-3609.
4. Freborg AM, Li, Z, Ferguson BL (2016) Using Heat Treat Simulation to Characterize Sensitivity of Quench Hardening Response in Hot Mill Steel Work Rolls, Proceedings of the 23rd IFHTSE Congress, Savannah, Georgia, USA, pp. 428-433.
5. Hellenthal L, Growth C (2005) Simulation of Residual Stresses in an Induction Hardened Roll. 23rd CADFEM Users’ Meeting, International Congress on FEM Technology with ANSYS CFX & ICEM CFD Conference, Bonn, Germany.
6. Krot PV, Bobyr SV, Dedik MA (2017) Simulation of backup rolls quenching with experimental study of deep cryogenic treatment. Int. Journal of Microstructure and Materials Properties 12(3-4): 259-275.
7. Bobyr SV, Bolshakov VY (2014) Modeli i kharakteristiki preryvistogo prevrashcheniya austenita v zhelezouglerodistykh splavakh Uspekhy fyzyky metallov, in Russian, 15(3): 123.
8. Bobyr SV, Bolshakov VI, Sharfnadel SA (2016) Analysis of the eutectoid transformation into carbon steel on the basis of positions of non-equilibrium thermodynamics. Material science. Nonequilibrium phase transformations. Sofia, Bulgaria 4: 30.