Shaheen Ahmed

doi:10.19080/CTCMI.2018.02.555591

Opinion

Information Theoretic Framework for MRI Preprocessing, Multiclass Feature Selection and Segmentation of Brain Tumors

Shaheen Ahmed*

Department of Behavioral and Brain Sciences, University of Texas at Dallas, USA

Submission: April 10, 2018; Published: May 08, 2018

*Corresponding author: Shaheen Ahmed, Department of Behavioral and Brain Sciences, University of Texas at Dallas, Texas, USA.

How to cite this article: Shaheen A. Information Theoretic Framework for MRI Preprocessing, Multiclass Feature Selection and Segmentation of Brain Tumors. Curr Trends Clin Med Imaging. 2018; 2(4): 555591. DOI: 10.19080/CTCMI.2018.02.555591

Abstract

Multiresolution texture features such as fractal dimension (FD) and multi fractional Brownian motion (mBm) have shown to offer robust tumor and non-tumor tissue segmentation in brain MRI. Multiclass Kullback Leibler Divergence (KLD) for feature selection can effectively select features for tumor, cyst and non-tumor tissues in multimodal MRI. In this work, we propose an information theoretic framework for improved brain tumor segmentation. Our proposed method combines all necessary steps such as MRI in homogeneity correction, feature extraction, multiclass feature selection and tumor, cyst and non-tumor tissue segmentation respectively in an integrated framework. Our integrated framework allows one to observe effect of each step in the end tumor segmentation results. Finally, we evaluate our method using 12 patients in T1, T2 and FLARI modalities.

Keywords: Brain tumor; Feature selection, MRI, Expectation-maximization, Fractal features; Multiforme; Glioblastoma

Abbrevations: MRI: Magnetic Resonance Imaging; GBM: Glioblastoma Multiforme; KLD: Kullback Leibler Divergence

Introduction

In the last decades, Magnetic Resonance Imaging (MRI) has been established as an important imaging modality in the diagnosis of brain tumors. Brain tumors such as Glioblastoma Multiforme (GBM) are a leading cause of solid tumor related cancer in adults, with less than 5% of the patients surviving five years after diagnosis [1]. GBM tumors are characterized by abnormal and uncontrolled cell proliferation, necrosis and vascular proliferation [2].

Researchers have focused on robust techniques for detection of tumors in MRI based on feature extraction and segmentation. However, two important confounding factors complicate the detection of tumors. First, intensity in homogeneity can cause a variation in intensity of a particular tissue across the field of view [3], and second, the intensity of a single voxel may be composed of signal from more than one distinct tissue type [4]. The most basic tissue-segmentation method is global intensity thresholding. This assumes a voxel intensity can be identified which assigns each voxel into a background class (voxels less intense than the threshold) or a foreground class (voxels more intense than the threshold). It may be possible to correct such intensity variation prior to segmentation. An alternative approach is to use local (adaptive) thresholding where the intensity threshold is variable and is computed over sub images or over a region of interest around each voxel. Feature extraction segmentation involves extracting of characteristic parameters based on correlation, contrast, homogeneity, isotropy, shape around neighboring pixels. Among texture feature, fractal analysis has been successful capturing the intricate and complex tumor pattern [5]. Further, multifractional Brownian motion (mBm) feature effectively models spatial varying heterogeneous tumor texture at different scale [6,7].

Automatic algorithms combines MRI in homogeneity correction for anatomical structure, registration and segmentation using atlas-based approach. These works mostly use EM method to obtain appropriate parameters for intensity correction, feature selection and registration transformation between atlas and MR images with lesions. Pohl et al. [8] have combined registration, intensity correction and segmentation of thalamus region in EM framework [8]. Well et al. [9] present methods to correct MRI intensity in homogeneity and segment MR images [9]. Gooya et al. [10] investigate brain tumor growth modeling, atlas registration and segmentation of brain tumors in EM framework [10] and considers tumor growth and deformable registration while registering a normal brain atlas with images of brain tumor patients for tumor segmentation [11]. Leemput et al. [12] developed fully automatic segmentation of brain MR images by statistical classification using an atlas prior both for initialization of probability density functions and also for geometric constraints, solved as an EM algorithm [12]. The method has been shown to be very robust and highly reproducible for normal brain images but fails in the presence of large pathology

In this work, we propose an integrated EM framework for feature-based brain tumor segmentation without the need for atlas-based image registration. Furthermore, we investigate improved tumor segmentation by delineating cyst tissue from tumor clusters in the same framework. The tumors may contain sphere like structures filled with fluid called cysts in addition to their solid components. When tumor has an associated cyst, there is generally a mass, or at least a thickening of the rim, visible on CT or MRI scans [13]. The segmentation of these surrounding tissues such as cyst and necrosis are very difficult due to the surrounding changes and distortion on MRI, location and size. We obtain in homogeneity correction, multiclass feature selection for tumor, cyst and non-tumor tissues and tumor segmentation exploiting a single EM framework. We validate our tumor and cyst segmentation results at pixel using different similarity metrics. Such an integrated information theoretic model can help in detection and robust segmentation of brain tumors.

Methods and Materials Participants

A data set of 12 patients was collected from the publicly available Cancer Imaging Archive (http:// www. cancerimagingarchive.net\) database for our study. The patients underwent T1- contrast, T2 and FLAIR acquisitions. The acquisition parameters were: Magnetic field strength = 3T, Flip angle = 90-degree, slice thickness = 5mm. The scan parameters for T1- weighted image are: TR = 168ms, TE = 8ms; the scan parameters for T2-weighted image are: Turbo Spin Echo, TR = 6430, TE = 114ms, 14 echoes/TR; scan parameters for FLAIR images are: TR = 9500ms, TE = 133ms.

Mathematical computation

The overall flow diagram of the method is shown in Figure 1. We use a Bayesian approach to estimate the bias field in MR intensity image. The method assumes a Gaussian distribution for the different tissues or classes. The bias field estimate is determined by applying a linear operator to the mean residual field. The parameter for linear operator is determined by the mean covariance of the tissue class intensities and the covariance of the bias field [9]. Once the bias field is corrected, we apply low pass Gaussian filter for correcting the in homogeneity in MR images. After in homogeneity correction we obtain multi resolution fractal (texture) features such as FD and mBm from the normalized images in T1, T2 and Flair modality. The best feature was selected based on the largest distance obtained by Kullback Leibler Divergence (KLD) for tumor, cyst and non-tumor regions, for specific features [14]. Finally, support map or probability map is constructed containing the mean and variance associated with a pixel for the best features. The labeling of map for each cluster offers the segmentation for the associated classes which in turn is represented by the best features. The detail steps of our model are discussed next.

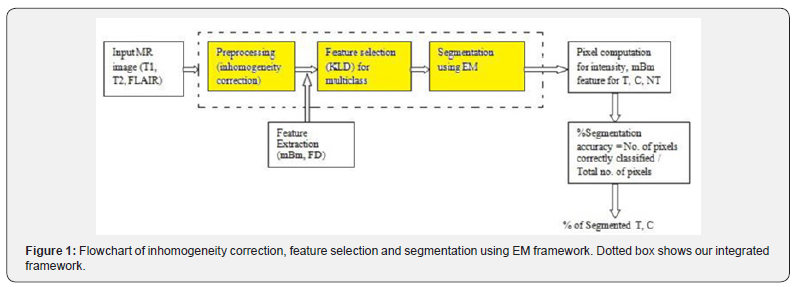
Information theoretic modeling for in homogeneity correction, feature selection and segmentation

In this work, we obtain an EM framework for computing the in homogeneities B and feature selection FS for MR images I. It is difficult to compute these two parameters without considering any hidden variable. We assume segmentation G as a hidden variable. When properly defined, the EM framework gives two important guarantees. First, each iteration yields an improved estimate of (B, FS) as measured by Eqn. (1). Second, the algorithm converges to local maxima of the objective function. The conditional probability distribution function describing I is given as P(I, B, FS,G) . We want to estimate B and FS from this framework which is given as,

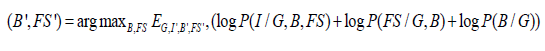
Both in homogeneity and feature selection can jointly affect the segmentation in MRI. However, in this work, we assume B and FS as separate parameters for simplicity of modeling. The optimization procedure decomposes Eqn. (1) based on the following independence assumptions. First, we assume the independence of I with respect to FS conditioned on T and B. We can therefore characterize each anatomical structure with an intensity distribution based on the tissues or classes which is not influenced by the mapping between the atlas and image space. Secondly, we assume FS independent of B conditioned on T. Finally, we assume independence of B with respect to T as the image in homogeneities are caused by the radio frequency coil of the scanner. Thus, it simplifies to the following,

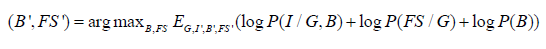
The hidden variables G = {G₁, G₂,...., G_n} are the number of segments for each pixel ‘x’ denoted by Gx and take values from the set of k-dimensional unit vectors e = {e₁, e₂,...., e_k} where x k G = e , meaning that x pixels belong to tissue k or cluster k . The E step is equivalent to calculating the probability map in the presence of hidden variable G and given the estimates of (Bx ', FS ') for a particular tissue k using Baye’s rule as follows,

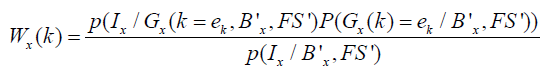
The M-step maximizes the estimates parameters B′ and FS′ on probability maps Wx(k) and are given as, and

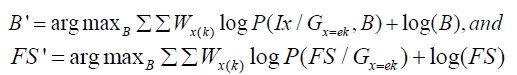
Estimating the intensity in homogeneities: Consider Eqn. (2) to define in homogeneities as follows,

where k γ , k μ are the mean and variances for a particular tissue, numbers of pixels for each class to Bayes classifier and obtain Ix is value of intensity feature at pixel x, x β is the bias field at the pixel x for particular tissue or class.

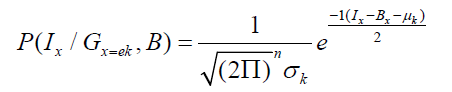
Estimating the Feature Selection

Feature selection using KLD is given as

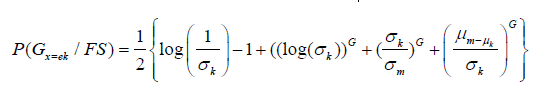
Where, σ_m , σ_k , μ_m , μ_k are the mean and variance of different tissues or classes. The segmentation G depends on the best feature selected using KLD. The KLD represents the conditional probability for two classes or tissues which are tumor/non-tumor, tumor/cyst and cyst/non-tumor. The KLD considers the mean and variance for the two classes or tissues for a particular texture feature and these means and variances are updated during M step. The segmentation for different tissues is related with the updating of probability maps which are updated for in homogeneity and feature selection.

Estimating segmentation accuracy

The selected best features are utilized for finding the number of pixels for tumor, cyst and non- tumor tissues. These pixels are used as the input to Bayes classifier to obtain the posterior probabilities for respective tissues. We then find segmentation accuracy based on posterior probabilities. Note we have two major types of features in this study such as intensity and texture (mBm or FD) that can be selected as the best to represent any given tissue. Therefore, we show the segmentation accuracy computation for these two features below.

Segmentation accuracy using intensity feature: The segmentation accuracy using intensity feature can be obtained by computing the number of pixels correctly classified using a Bayes Classifier. We compute the number of pixels for every class such as tumor, cyst and non-tumor. We input total number of pixels for each class to Bayes classifier and obtain the posterior distribution for each class. We then calculate the number of pixels correctly classified based on posterior value, and hence, the tumor segmentation accuracy.

Segmentation Accuracy using mBm Feature: Texture features such as FD and mBm are non-linear feature extraction process. Therefore, there does not exist one-one relationship between texture features and the final tumor pixels. In order to compute pixel level accuracy for tumor segments using texture features, we consider sub images which cover the tumor region. We then obtain a suitable threshold values for locating interior pixels and exterior pixels in those sub-images. Following our prior work (12), to obtain number of tumor pixels for mBm feature case, we obtain covariance image and decompose the variance image using multi resolution wavelet theory. The resulting decomposed image is divided into sub images of size 8x8. We then compute the wavelet coefficients for all the pixels in the subimages. We obtain the histogram for each sub images given as,

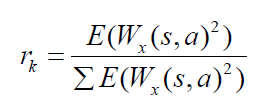
The histogram offers variation in wavelet coefficients for the sub images. We then obtain a suitable threshold for interior pixels and exterior pixels for selecting T, or C sub images. We finally compute the correctly classified pixels based on posterior value.

Results and Discussion

Segmentation results using our integrated model

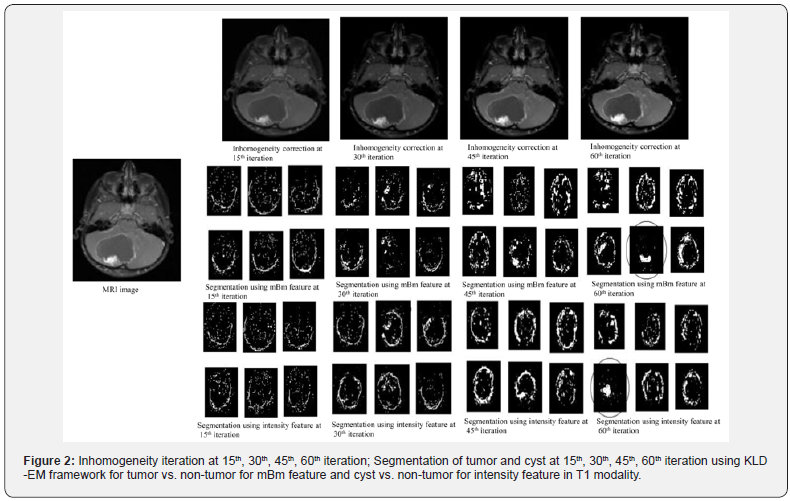
Figure 2 shows the in homogeneity correction results at different iterations using integrated EM- based framework for MR image of patient with tumor in T1 modality. The integrated EM model in this work offers mBm and intensity as the best features for tumor vs. non-tumor and cyst vs. non-tumor segmentation respectively. Note in our prior work, mBm is identified as the best feature for segmenting tumor from non-tumor tissues using two classes KLD [7]. In a recent work, we extend two-class KLD to multiclass KLD for best feature selection among tumor, cyst and non-tumor tissue types and find that the best feature for tumor vs. non- tumor segmentation is mBm while that for cyst vs. nontumor is intensity [14]. Figures 2 shows the corresponding tumor segmentation results for mBm feature using our integrated model. We observe that good tumor segmentation is obtained at 60th iteration with cluster 5. Further, Figure 2 shows the cyst segmentation and the best result is obtained in cluster 4 also at 60th iteration.

Segmentation validation

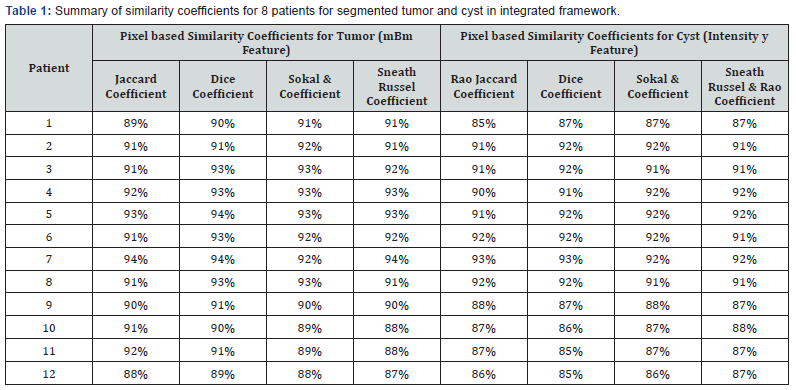
Table 1 shows the similarity overlap coefficients of the tumor segments obtained using our model and the radiologists’ ground truth for all 12 patients. Table 1 suggests that tumor segmentation accuracy varies between 91% - 94% using all four differ overlap metrics while that for cyst varies between 90% - 93% respectively. Note for our integrated model proposed in this work, we can perform in homogeneity correction, and feature selection; and observe the effect of these steps on tumor segmentation simultaneously.

Conclusion

In this work we propose an integrated EM model to combine three steps such as in homogeneity correction, feature extraction and feature selection for brain tumor segmentation. To achieve segmentation validation, we obtain pixel counts for segmented tumor or cyst tissues and use different similarity coefficients to measure overlap between the segmented tissues with those of the radiologists’ ground truth at the pixel level. The overlap measures show about or above 90% segmentation validation performance for both cyst and tumor tissues. To the best of our knowledge, an integrated model for MRI preprocessing, feature extraction, and feature selection for tumor and cyst segmentation has not been studied until now. Such an integrated framework can be useful for brain tumor detection and adjuvant therapy planning.

CTCMI.MS.ID.555591

Our Media Partner

CTCMI Menu

Useful Links

Downloads