Research Article

An alternative model to the generalized forced quantitative randomized response model that uses data collection

Altaf Ahmad Bhat¹,Tanveer A Tarray² and Zahoor A Ganie³

¹Department of General Requirements, University of Technology and Applied Sciences, Salalah-Oman

²Department of Mathematical Sciences, Islamic University of Science and Technology , Kashmir – India

³Department of Electrical Engineering, Islamic University of Science and Technology , Kashmir – India

Submission: April 13, 2023; Published: May 03, 2023

*Corresponding author: Altaf Ahmad Bhat, Department of General Requirements, University of Technology and Applied Sciences, Salalah-Oman

How to cite this article: Altaf Ahmad Bhat,Tanveer A Tarray and Zahoor A Ganie. An alternative model to the generalized forced quantitative randomized response model that uses data collection. Biostat Biom Open Access J. 2023; 11(2): 555808. DOI: 10.19080/BBOAJ.2023.11.555808

Abstract

As alternatives to the generalized forced quantitative randomized response model that is provided in this research, we have offered two other randomized response models. We have looked into the characteristics of these suggested models and discovered that they are more effective than the ones that are already in use. The previous estimate relied on two independent samples and randomized response models; however, this method raises survey expenses. As a result, we provide two different randomized response models based on a single sample that solves this problem without raising the survey’s expenses.

Keywords: Randomized Response Model; Simple Random Sampling With Replacement (SRSWR); Mean Squared Error; Scrambled Response; Sensitive Variables.

AMS Subject Classification: 62D05

Introduction

Politicians and social scientists are regularly interested in gathering data on stigmatizing issues, and many surveys’ aim parameter ends up being the population fraction of people who have a sensitive trait. Sometimes respondents are asked delicate questions, including as on their normatively charged beliefs and if they engage in humiliating behaviors like browsing pornographic websites or criminal ones like tax fraud. In certain surveys, participants may be questioned whether they have ever had an abortion, about their history of drug misuse, whether they have ever engaged in homosexual behavior, or whether they have ever been infected with AIDS. Respondents may decide not to answer a question or may knowingly give incorrect information if they believe their responses may be used against them. Direct questioning techniques may result in denials and slanted responses that are likely to result in a significant underestimating of . The randomized response method (RRT), developed by Warner in 1965, is frequently used by researchers since it has been shown in several field studies to significantly boost respondent participation. These researchers include [1-17], who suggested a multiplicative mod

The Suggested Randomized Response Model

Observing the optimum value of F, we select two appropriate values of F as

Mathematically, the distribution of the responses will

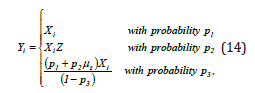
where iX denotes the true response, ZXi denotes the scrambled response and 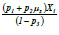also denotes the scrambled response. Thus we have the following theorems:

Theorem- 5.1- An unbiased estimator of the population mean μ_x is given by

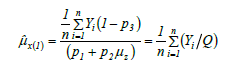
which proves the theorem.

Remark- 5.1- As the quantities p₁, p₂, p₃ and μ_z are known, therefore the proposed randomized response model (RRM-I) and then the proposed estimator can be used in practice without any difficulty.

Special Cases

Case-I: If p₁=0, p₂=1, p₃=0 then the proposed model turns out to be the existing model.

Case-II: If p₁=p, p₂=(1-p), p₃=0 then the proposed model becomes one of the already suggested model.

Efficiency Comparison:

This section provides the condition in which the proposed estimator 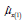is more efficient than the existing estimators.

From the above equations, we have that

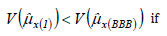
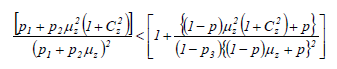
It is to be observed from above that

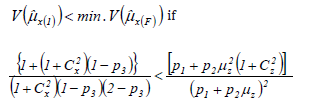
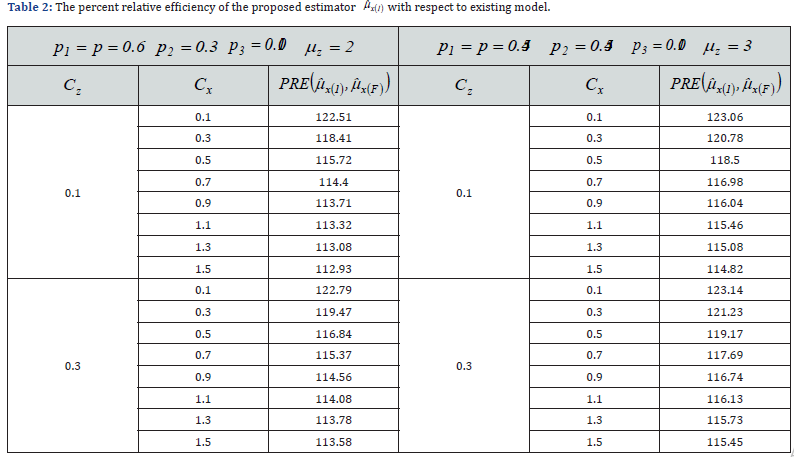
for computing PREs of the proposed estimator 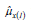with respect to existing models. Findings are given in (Table 1 & 2).

It is observed from Tables 1 and 2 that the gain in efficiency is achieved by using the suggested estimator 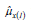over the existing estimator 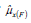is larger.

It is further observed from Tables 1 and 2 that the percent relative efficiency of the suggested estimator 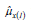with respect to existing are larger than 100% for the selected parametric values as given in (Table 1 & 2).

Conclusion

It has been thought about how to estimate the population mean of the sensitive quantitative variable. This study explains how the randomized response model might be enhanced. The unbiased estimate of the mean of a sensitive quantitative variable has been proposed, and the characteristics have been examined. Recommended estimator has been demonstrated quantitatively to be more effective than the existing estimator. It’s noteworthy to note that there are no issues using the proposed estimator more effectively in practice.

References

1. Bar Lev SK, Bobovitch E, and Boukai B (2004) A Note on Randomized Response Models For Quantitative Data. Metrika 60: 255-260.
2. Eichhorn BH, Hayre LS (1983) Scrambled Randomized Response Methods For Obtaining Sensitive Quantitative Data. Journal of Statistical Planning and Inference 7(4) : 307-316.
3. Gjestvang CR, Singh S (2006) A new randomized response model. Journal of the Royal Statistical Society Series B 68(3): 523–530.
4. Gjestvang CR, Singh S (2007) Forced quantitative randomized response model: a new device. Metrika 66: 243–257.
5. Sing S, Singh R, Mangat NS (2000) Some alternative strategies to Moor’s model in randomized response model. Journal of  Statistical Planning and Inference 83(1): 243-255.
6. Singh HP, Tarray TA (2012) A Stratified Unknown repeated trials in randomized response sampling. Communications for Statistical Applications and Methods 19(6): 751-759.
7. Singh HP, Tarray TA (2013) An alternative to Kim and Warde’s mixed randomized response model. Statist. Oper. Res. , 37(2): 189-210.
8. Singh HP, Tarray TA (2014) An alternative to stratified Kim and Warde’s randomized response model using optimal (Neyman) allocation. Model Assisted Statistics and Applications 9(1): 37-62.
9. Singh HP, Tarray TA (2022) Two - stage stratified partial randomized response  Communications in Statistics - Theory and Methods.
10. Singh HP, Tarray TA (2016) An improved Bar – Lev, Bobovitch and Boukai randomized response model using moments ratios of scrambling variable.  Hacettepe Journal of Mathematics and Statistics 45(2): 593-608.
11. Singh S, Sedory SA (2013) A new randomized response device for sensitive characteristics: an application of the negative hypergeometric distribution. Metron 71: 3-8.
12. Tarray TA, Singh HP (2015) A stratified randomized response model for sensitivity characteristics using negative binomial distribution . Investigacion Operacional 36(3): 268-279.
13. Tarray TA, Singh HP (2016) New procedures of estimating proportion and sensitivity using randomized response in a dichotomous finite population. Journal of Model Applied Statistical Methods 15(1): 635-669.
14. Tarray TA, Ganie ZA (2022) A New Data Gathering Exponential Type Ratio Estimator for the Population Mean. Journal of Scientific Research and Reports 28(10): 148-153.
15. Tarray TA, Ganie ZA, Baziga Y (2019) An improved mathematical model applying practicable algorithms. Journal of Applied Science, Engineering, Technology, and Education 1(2): 114-118.
16. Tarray TA, Ganie ZA and Baziga Y (2021) Stratified Optional Mathematical Model. Renewable Power for Sustainable Growth. Springer 723: pp. 307-313.
17. Warner SL (1965) Randomized Response: A Survey Technique for Eliminating Evasive Answer Bias. J. Amer. Statist. Assoc., 60(309):63-69.