Consider Statistics from Its Mathematical Foundation
Xi Chen*
PharmClint Co. Ardsley, USA
Submission: March 18, 2019; Published: May 01, 2019
*Corresponding author: Xi Chen, PharmClint Co. Ardsley, New York, USA Biostat Biometrics
How to cite this article: Xi Chen. Consider Statistics from Its Mathematical Foundation. Biostat Biometrics Open Acc J. 2019; 9(4): 555767. DOI: 1 10.19080/BBOAJ.2019.09.555767
Abstract
The confidence interval (CI) approach widely used in clinical trial analysis has many serious statistical flaws, if such problems are not well addressed, all statistical conclusions drawn from the clinical trial analysis will be debatable. Although the challenge is completely on a theoretic basis, it touches the foundation of the statistical analysis. Any analysis based on multiple statistical measures will be anything but not the mathematical science.
Keywords: Confidence interval; Distribution; Measure; Model
Abbrevations: SUP: Superiority; NI: Non-Inferiority; SM: Study Medication; AC: Comparator; PDF: Probability Density Function; EQ: Equivalence; MCID: Minimum Clinical Important Difference; INF: Inferiority; MDD: Minimum Detectable Difference; LRT: Likelihood Ratio Test; PMF: Probability Mass Function
Introduction
In socialist China, there is a well known slogan, the practice is the only criterion to test a knowledge. The purpose of this manuscript is not to show it to be true or false, such a slogan is not applicable to certain fields. A typical situation is mathematics, it is a field requiring the abstract logical reasoning, there is no physical model with which the practice can be well performed.
Mathematics is considered to be the most accurate science, any single counterexample is enough to destroy a whole set of theory. To test the correctness of a mathematical theory, practice may not be well defined. A mathematical theorem can be tested against a mathematical axiomatic system. A mathematical axiomatic system is a set of commonly accepted truth which can not be and does not need to be proved.
Statistics is a branch of applied mathematics, it will follow the same pattern as mathematics. For an applied statistician, the theoretic foundation is generally overlooked. But, it has to be crystal clear, without a theoretic foundation, the statistical analysis can be anything but not science. Moreover, if a government agency controlling the regulation does not follow the steps compatible with the theoretic axiomatic system, all the pharmaceutical products went through the clinical trial can be challenged.
In the publication [1], the axiomatic system for statistical analysis has been discussed. People not familiarized with the technical detail may have a difficult time to realize its relationship to the conventional confidence interval (CI) approach in statistical inference. In practice, statistical analysis is generally performed base on approximations, the meaningful counterexample is generally hide behind the rounding error. It is not a mathematical logical reasoning. For example, the Goldbach’s conjecture is almost true may not be a meaningful statement, since a single counterexample may approve the conjecture to be false. Almost is a concept associated with approximation, it is a key difference between mathematics and applied statistical analysis. This manuscript will show the existence of the logical hole in conventional analysis behind the numerical approximation [2].
Conventional CI approach
We consider a noninferiority (NI) trial to compare a study medication (SM) against an active comparator (AC). Assume the cure rate of SM follows a normal approximation
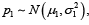
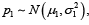
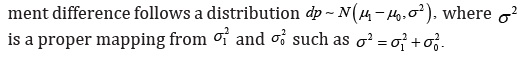
Example under consideration
For a non-inferiority (NI) trial under consideration, it is assumed that the overall rate will be 80%,p= the NI margin is set to be 10%.Δ= The trial will be conducted with two side type I error of 5%,α= and one side type II error control as be 120%.
Sample size estimation
The study hypothesis is set up as,
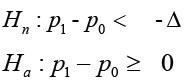
There are three ways to estimate the sample size, corresponding to nH to be true, aH to be true and the combination of the two.
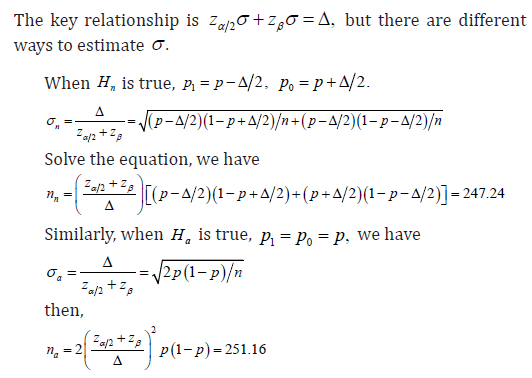
Moreover, it is noted that the type I error was calculated based on the distribution associated with null hypothesis, and the type II error was calculated based on the distribution associated with the alternative hypothesis, from 2,nazzαβσσ+=Δ the sample size cn will be
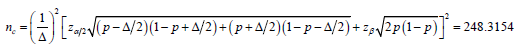
For the safety of the trial, we take the ceiling of (),,nacnnn and choose the largest among the three, we have n=252.
Simulated trial outcome
To find a counterexample, only an extreme case will be enough to show the arguments. We assume that there were 198 subjects in SM arm be cured, and there were 206 subjects in AC
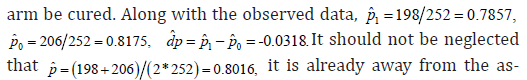
CI analysis
Along with the observed data, the estimated CI is constructed
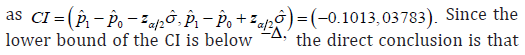
It is noted that the estimation ˆσ is different from either ˆnσ or ˆ,aσ it is calculated as

The challenges to the statistical inference
The above analyses obviously involved some approximations. For example:
i. The mean of the calculated CI is with respect to 10ˆˆ0.03174603,pp−=− not −Δ or 0. If possible
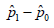
ii. The calculation of ˆσ is with respect to
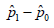
iii. If nH is true, ()()2,fxNσ=−Δ is considered to be the correct model. The threshold for the upper bound of the accept region is 20.0307048,nzασ−Δ+=− it is associated with a measure ().fxdx The estimated CI is based on ()()2ˆˆˆ,,gpNdpσ= with a measure ().gpdp One analysis associated with two measures are problematic.
iv. Bernoulli model is a member of one parameter family, but the normal model belong to the two parameter family. The CI approach depends upon a property of a normal model, the estimation of its mean is independent to the estimation to its variance. When a Bernoulli model is approximated by a normal model, the approximation error is inevitable.

vi. The CI approach is sensitive to the study sample size and the sample size depends upon the initial estimation for ,p any deviation from them may change the trial conclusion. Obviously, the observed ˆp is only available upon the sampling is completed, it is almost for sure that there is a difference between this observed ˆp and the p used in calculate the sample size.
vii. To face the challenges, two important properties are expected, the first is the adaptive property, the conclusion criteria will change along with the parameter changes; the second is the asymptotic property, the trial conclusion will not change along with the increase of the sample size.
Multiple statistical measures
It is shown that the CI approach involved three distributions. They are:
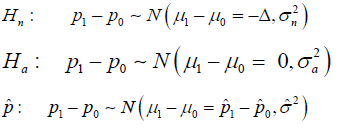
Where nH implies the null to be true, aH implies the alternative to be true, and ˆp implies the estimations during the trial.
As discussed in [1], the involvement of the three distributions in an analysis implies the introduction of three statistical measures, since the measure is defined as (),fxdx where ()fx is the probability density function (PDF) of the random variable. The multiple statistical measures is definitely against the mathematical axiomatic system, it is a flaw which destroys the credibility of the whole project.
Recall the design of the trial, the sample size was calculated under the assumption that nH to be true or aH to be true respectively, but in the estimation, none of them was actually tested. Checking if the calculated CI cover −Δ or 0 could not be considered as
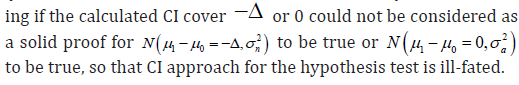
Model based clinical trial design
The hypothesis test based on uniform statistical measure does exist, but it is based on a different setup of the hypothesis.
Study hypothesis setup
Within a model based clinical trial, for either a noninferiority (NI) study or a superiority (SUP) study, the study hypothesis has the same form
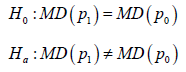
the efficacy of SM or AC. MD is used in both sides implies that both SM and AC are assessed by same type of the distribution. The only difference is the mapping between the trial outcome and the trial conclusions. For each trial, there are three possible outcomes, equivalence (EQ) implies 0H is confirmed, or say aH is rejected. Superiority (SUP) implies aHis confirmed and 10.pp> Inferiority (INF) implies aH is confirmed and 10.pp< Naturally, Noninferiority (NI) implies EQ or SUP conclusion.
The formulation of the model
With Bernoulli model for each subject, the probability mass function (pmf) can be written as
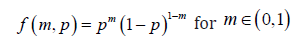
where 1m= represents a cure, and 0m= represents a failure, for n subjects, the likelihood function can be written as

For the specific clinical trial under our consideration, it is known that ()ˆ1982062*2520.80159p=+= and 252.n= It can be shown that the critical ratio is *0.0674556.ε= Since ˆ0.03175*,dpε=< we get a conclusion that EM to be a better model, the NI of SM to AC has been shown.
Moreover, if the statistical MCID 0.05SD= is expected, assume 0.8,p= the table in [1] shows to reach *,SDε< the sample size has to be increased to 471.
Findings from the model based analysis
It has been shown in previous section that when there is a treatment difference of 10ˆˆ3%,pp−≈ the trial conclusion was that SM is inferior to AC by 10%. Although the rejection was near the border line, the 10% treatment difference is far from the actual observation, it was not within the common sense for most people who read the report.
In the model based analysis, the likelihood ratio test (LRT) was applied. According to the Neyman-Pearson lemma, LRT is the uniformly most powerful test among all the hypothesis tests with given type I error control .α It is shown that with same test data, with LRT, the minimum detectable difference (MDD) *0.06947556,ε= the 3% treatment difference is far short than the cutpoint. The LRT showed the noninferiority of SM compared with AC. The model based approach not only changed the trial conclusion, it used the data information in a more efficient way./p>
Logical difference between CI and Model based approaches
Along with the CI approach in statistical analysis, there is an important logical hole which could not be overlooked. I am always cheating is a statement with a logical hole, since there is no criterion for its truth or false. If I am a cheater, this statement tells the truth; if I am not, the statement can only be false.
Similarly, to test a null hypothesis under the assumption of true Hn is also problematic. Using the conventional CI approach to do a hypothesis test, under the assumption of true Hn and reject Hn is ill-fated. For same reason, under the assumption of true Hn and to confirm Hn is also problematic. In fact, under the assumption of true ,Hn the hypothesis test itself is already redundant. But, without the assumption of true ,Hn the so called type I error control lost its foundation. There is only one exception, no matter which one between Hn and aH to be true, the statistical distribution used for statistical inference remains the same, so the assumption itself is redundant. It is noted that the model based analysis used such a distribution, it is the key difference between the CI based analysis and the model based analysis.
The problem of multiple statistical measures can be found in many other types of the clinical trial design. For example, some oncology clinical trial reports claimed both survival rate and risk ratio. In fact, the two statistics came from different statistical models, the survival rate came from the Kaplan-Meier analysis and the risk ratio came from the Cox regression model, they are associated with different statistical measures.
Historic Lessons
In 1897, based on a finding of a physician and an amateur mathematician Goodwin, a method to square a circle has been introduced into a pending bill in Indiana General Assembly [4], it does imply various incorrect value of π the ratio of the circumference of a circle to its diameter. Thanks to Prof. Waldo of Purdue University for his intervention, it has never become a law. The incidence is generally named the Indiana π bill, the direct lesson people learnt was never using law to regulate a scientific truth. In fact, Lindemann did provide a rigorous proof for the impossibility to square a circle with only compass and straightedge, a better approximation of πwas known before that time.
The scientific discovery is an endless process, the model based clinical trial introduced in previous section is a way to define and test non-inferiority based on a unique statistical measure, but it is by no means the only way with such a property. Along with the progress of the mathematical science, it seems to be inappropriate for government agency to regulate the statistical hypothesis test in clinical trial, such as through the guidance for clinical trial.
It is noted that ICH document has also explained the concept of superiority and non-inferiority, but it did not go into the mathematics detail, its explanation is only through the plain English texts. On the other hand, ICH is just a harmonization, or say the statements of the common sense. It is different from the law. In certain rare cases, some documents may contain the technical detail. For example, the international system of units, the description of the units can be very technical. But, it is by no means a law, instead, it can be considered as an axiomatic system. The axiomatic system is the truth, they could not be and do not need to be proved.
The U.S. Constitution has set up the principle of the power separation, the power to interpret the law belong to the judicial branch, the government agency has only the obligation to execute the law. The government agency definitely has the right to express their understanding to the law, but the guidance is no more than an attorney statement, it should not be considered as the law.
On the other hand, in the beginning of the last century, the black body radiation was studied by many researchers. Wilhelm Wien did an extensive work on the issue, and his equation fit the experiment curve very well. The minor difference in the curve was commonly believed to be a random error. He received the 1911 Nobel Prize in physics for his achievement. But, his small mismatch motivated another researcher, Max Planck, to dig into it, and it was the start of the era for quantum mechanics, and he received the same prize in 1918 for his genius idea. The lesson taught us that the small mismatch does not teach us nothing, it told us that the scientific truth may hide behind the small mismatch.
Critics to current guidance
In the past years, FDA has issued a series of statistical guidance for industry, express their understanding regarding non inferiority and superiority [5]. Obviously, they had difficulties to dig into the concepts, the document tried to get into the technical detail without giving an accurate mathematical definition of SUP and NI respectively.
Definition of efficacy measure
For a NI trial, the guidance considered the following hypothesis test,
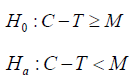
where C is the effect of AC and T is the effect of SM, M is the margin. The problem is that this hypothesis could not be tested along with the CI approach, but the examples showed in the figures are completely on the foundation of the CI approach. More specifically, the theoretical linkage between the hypothesis and the figure is not shown.
For the example given in the figure, in the common sense, the efficacy is measured by the real number system, it is different from the quantum mechanics. So, 0.5 can also be considered as efficacy, not necessarily to be an integer
Margin and MCID
On the other hand, the guidance defined the margin M, either M_1or M_2, in plain English text. But it is short to be an accurate mathematical definition. In the common sense, to express the difference between two random variable, the convenient measurement is its first moment. The lower and upper bound of the CI can never be used to characterize the difference between two random variable.
In the publication [2,3], the concept of the margin (M) has been replaced by the Minimum Clinical Important Difference (MCID), either statistical MCID ()SD or constant MCID ().cD SD are cD are defined with respect to the means of the distribution, not associated with the lower or upper bound of the CI. Within a common sense, a male athlete is taller than a female athlete should be considered as a valid statement. This statement should be understand on average basis, a male gymnastics is almost sure to be shorter than female WNBA basketball player, it will not make the statement nonsense. The concepts of SUP and NI should be understand in similar way.
Test NI and SUP at the same time
The guidance also has a section to discuss testing Non-Inferiority and Superiority in a single trial, but the texts seems applicable to test SUP in a NI trial. A natural question is if it is possible to test the NI property in a SUP trial. In fact, along with CI approach, the distributions associated with NI and SUP hypotheses are different, so the two analyses are associated with different measure. The so called type I error is with respect to the distribution under consideration. In model based analysis, for both NI and SUP trials, the statistical hypothesis has been unified into the same form, and the associated distribution remains unchanged. It effectively avoids such the problem.
Asymptotic and adaptive properties
There are two other important properties a clinical trial methodology should have, but the guidance did not require them. The first is the asymptotic property, and the second is the adaptive property. In a clinical trial, when the sample size reached a certain level, the trial conclusion should not change along with the increase of the sample size. The increase of the sample size can only increase the trial precision, not able to change the trial conclusion. Such a property is named the asymptotic property.
Another property should be required is the adaptive property. When the trial observed data does not meet the pre-assumption of the trial design, for example, the p was assumed to be 80%, but the observed ˆ0.8016.p= The statistical model used for analysis should be changed accordingly, since it has an impact on the trial conclusion. It is shown in [2], the model based analysis has both of the asymptotic and adaptive properties, it is one of the key advantage of model based analysis compared with the CI based analysis.
Conclusion
The purpose of this manuscript is not to blame any one who made mistake in defining and testing superiority and noninferiority. The statistical guidance issued by government agency should not be considered as legislation, it only reflects the current understanding of them to the mathematical truth.
References
- Chen X (2018) Statistical model and clinical trial analysis. Biostat Biometrics Open Acc Journal 8(5): 555750.
- Chen X (2013) A non-inferiority trial design without need for a conventional margin. Journal of Mathematics and System Science 3: 47-54
- Chen X (2013) The generalized clinical trial outcomes. Journal of Mathematics and System Science 3: 167-172.
- Hallerberg A (1977) Indiana’s squared circle. Mathematics Magazine 50: 136-140.
- FDA (2016) Non-Inferiority Clinical Trials to Establish Effectiveness.






























