Statistical Model and Clinical Trial Analysis
Xi Chen*
PharmClint Co. Ardsley, USA
Submission: October 04, 2018;; Published: December 20, 2018
*Corresponding author: Xi Chen, PharmClint Co. Ardsley, New York, USA
How to cite this article: Xi Chen. Statistical Model and Clinical Trial Analysis. Biostat Biometrics Open Acc J. 2018; 8(5): 555750. DOI:10.19080/BBOAJ.2018.08.555750
Abstract
The different setup of the clinical trial goals may lead to different statistical analysis methodologies and different trial conclusions. Some statistical methodologies used in the conventional clinical trial design are against the common acceptable probability axiomatic system. In the sense, the term superiority and non-inferiority are not only misleading, they are even not well established. To clarify these concepts and to find a feasible solution for clinical trial analysis, it is necessary to review the foundation of the statistical analysis and assumptions in common practice.
Keywords: Confidence interval; Distribution; Measure; Model
Abbrevations: SUP: Superiority; NI: Non-Inferiority; SM: Study Medication; AC: Comparator; PDF: Probability Density Function; Str: strict; EQ: Equivalence; MCID: Minimum Clinical Important Difference; Con: Conservative; Agr.: Aggressive; INF: Inferiority; MDD: Minimum Detectable Difference; LRT: Likelihood Ratio Test; PMF: Probability Mass Function
Introduction
The goal of the clinical trial analysis can be setup in different ways, they may lead to different set of statistical analysis methodologies, and even different statistical conclusions. The conventional clinical trial is to determine the superiority (SUP) or non-inferiority (NI) of study medication (SM) against a comparator (AC). This kind of the trial design used the confidence interval (CI) approach, and the trial design depends upon a prespecified SUP or NI margin. For simplicity, it is named CI based trial. A more objective way to present the trial goal is to determine the statistical model characterizing the treatment difference of SM against AC. The trial is named model based trial. The purpose of this manuscript is to investigate the impact of the trial goals on the statistical analysis inference and the conclusions [1].
Within a clinical trial project, if the random sample follows a Bernoulli distribution, the trial is generally named a Bernoulli trial. Although in practice, the statistical models such as the binomial distribution, the Poisson distribution and even the normal approximation are widely used, they are built up on a common Bernoulli foundation. For this reason, the following discussion is applicable to all the statistical setups [2].
Model
Probability axiomatic system
In Kolmogorov’s probability theory (6) the probability P of some event ,E denoted by (),PE is usually defined such that P satisfies the Kolmogorov axioms: Let (Ω,F,P) be a measure space with P(Ω)=1, the (Ω,F,P) is a probability space, with sample space ,Ω event space F and probability measure .
The Kolmogorov axioms can be further divided into the following three axioms: First axiom, P(E)>0 for any .φ≠E⊂Ω Second axiom, P(Ω)=1 Third axiom, any countable sequence of disjoint events 12,,EE satisfies 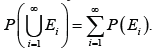
The Kolmogorov axioms led to several implications in the statistical analysis. For any statistical analysis, the sample space (Ω) and the probability measure (P) has to be kept unique and unchanged. Any element in event space (F) has to be properly defined. Any relaxation from these conditions may lead to the conclusion not on the common acceptable foundation, they will be beyond the scope of the statistical analysis.
A map qualified to be a measure
In statistical analysis, a measure on a set is a systematic way to assign a number to each suitable subset of that set. A properly defined probability measure should have the following properties:
I. Non-negativity. For all E in ,Ω P(E)≥0
II. Null empty set. P(φ)=0
III.
Monotonicity. If E1 and E2 are measurable sets with 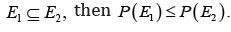
IV.
Subadditivity. For any countable sequence 123,,,EEE of sets nE we have 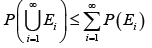
V.
Continuity from below. If 123,,,EEE are measurable sets and nE is a subset of 1nE+ for all ,n then the union of the sets nEn is measurable, and 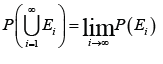
VI.
Continuity from above. If 123,,,EEE are measurable sets and for all ,n 1,nnEnE+⊂ then the intersection of nEnE+⊂> is measurable. Furthermore, if at least one of the nEhas finite measure, then 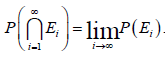
Theorem 1
A properly defined probability measure should be unique.
Proof: Let Ω be decomposed as 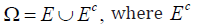 is the complement of .E For a properly defined measure ,P it is known that
is the complement of .E For a properly defined measure ,P it is known that  due to the third axiom. If there is a pair of probability measures, 12,PP≠ exists with
due to the third axiom. If there is a pair of probability measures, 12,PP≠ exists with 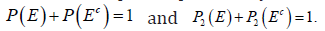 Let E=Ω and ,cEφ= we haveP1(E) = P2( E)=1, it conflicts to the known inequality
Let E=Ω and ,cEφ= we haveP1(E) = P2( E)=1, it conflicts to the known inequality 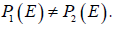
Some additional notes regarding axiomatic system
Within a statistical analysis project, there are some additional points should draw plenty of attentions. First, if a continuous random variable X is considered, along with a probability density function (PDF) f(x), the probability measure P is defined as f(x)dx The uniqueness of the probability measure basically requires f(x) to be unique, it is the key argument of this manuscript. Second, the axiomatic system is a commonly believed truth, it serves as a bible which does not need a proof. Any misunderstanding, expansion or relaxation will lead to theories beyond the discussion foundation. For example, Euclidean geometry follows five axioms, a minor change in the parallel axiom led to a complete different set of the geometric theory named the non Euclidean geometry. The communication between the Euclidean geometricians and non Euclidean geometricians are basically speaking different languages without a convincing translation, the debate needs to clarify which geometry to be the discussion topic, without such a foundation, the discussion is meaningless [3,4].
Definition of superiority and non-inferiority
In a Bernoulli clinical trial, assume the cure rate of SM to be 1p and the cure rate of AC to be 0,p the both arms of SM and AC are assessed by the same statistical model. The concepts of strict (Str.) SUP, NI and equivalence (EQ) are defined as follows:
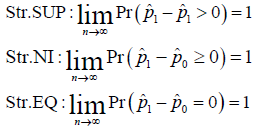
Where the hat represents the estimation. Without specified otherwise, all the estimations are maximum likelihood estimates.
Some additional notes may not be redundant, following (7), a statistical model is a set of probability distributions on the sample space .Ω The same statistical model implies that both SM and AC arms are evaluated with same class of distributions, for example, a Bernoulli distribution with parameter 1p or 0p respectively.
Generalized outcomes
Moreover, as it is shown in (2), along with a constant minimum clinical important difference (MCID), (Dc) the conservative (Con.) and aggressive (Agr.) SUP, EQ and inferiority (INF) are defined as follows:
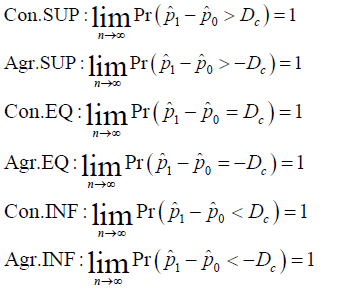
For convenience, the strict outcomes will generally be named as outcomes, the conservative and aggressive outcomes will generally be referred as the generalized outcomes. All of these properties are asymptotic properties. It is necessary to show that when the sample size is beyond a certain level, the statistical conclusion will not change along with the sample size and the trial conduction. Besides, since 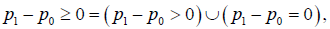 NI can be considered as the union of SUP and EQ. Besides, ,NIINF∪=Ωthe generalized NI can be derived from the generalized SUP and EQ, or from the generalized INF [5].
NI can be considered as the union of SUP and EQ. Besides, ,NIINF∪=Ωthe generalized NI can be derived from the generalized SUP and EQ, or from the generalized INF [5].
Under normal approximation, here is a key point to be mentioned, assuming σ2 is known, the strict outcomes are assessed by a model 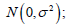 the conservative outcomes are assessed by a model
the conservative outcomes are assessed by a model 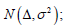 and the aggressive outcomes are assessed by a model
and the aggressive outcomes are assessed by a model 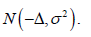
Conventional clinical trial practice
FDA guidance (4) refers to the CI based clinical trial design. Within a Bernoulli trial, assume the cure rate of the study medication (SM) be 1p and the cure rate of the comparator to be 0,p for a NI trial, the study hypothesis is
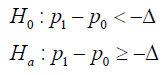
Following the FDA guidance, if 0H is true, SM is inferior to AC by Δ or more; if aH is true, SM is not inferior to AC by .Δ In most cases, the test for a treatment effect corresponds to showing that the lower bound of the two-sided 95% confidence interval (equivalent to the lower bound of a one-sided 97.5% confidence interval) for 10pp− is .−Δ This result shows that the effect of SM is not inferior to AC by .
Carefully review the description of the CI based NI trial, some natural questions may arise. At first, the name of noninferiority implies 100,pp−≥ to show 10pp−≥−Δis in fact a limited inferiority other than the non-inferiority. Secondly, how does the CI approach link with the hypothesis test is not quite clear. It is noted that the 95% confidence interval is formulated as 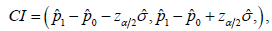 which was assessed by the distribution
which was assessed by the distribution 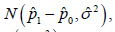 it is different from either distributions
it is different from either distributions 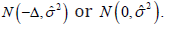
Uniqueness of the probability measure
The CI based trial analysis applied some operations in violation to the axiomatic system. The CI based trial is built upon the foundation of two distinct statistical distributions 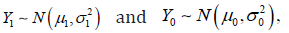 the treatment difference is defined as 10.dYYY=− Not losing the generality, dY follows a normal distribution
the treatment difference is defined as 10.dYYY=− Not losing the generality, dY follows a normal distribution 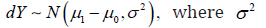 is a proper mapping from
is a proper mapping from 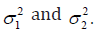
It is easy to see along with a Δ>0, 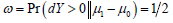 and
and 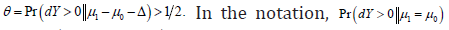 use
use  implies to use
implies to use It should be noted that both ω and θ are not conditional probabilities in traditional sense, they are still unconditional distributions. 0dY> and 0dY≤ are disjoint and
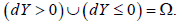 Based on the second and third axioms,
Based on the second and third axioms,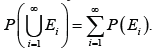 but
but 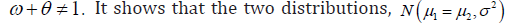 and
and 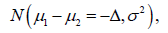 do not meet the requirements to construct a probability space, but they were actively used as constraints in the trial design. More specifically, such a constraint is reflected in the well known relationship of
do not meet the requirements to construct a probability space, but they were actively used as constraints in the trial design. More specifically, such a constraint is reflected in the well known relationship of 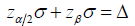 or the similar equation. This equation is widely used to determine the trial sample size, and the arbitrary increase of the trial sample size is not allowed in the current clinical trial practice [6].
or the similar equation. This equation is widely used to determine the trial sample size, and the arbitrary increase of the trial sample size is not allowed in the current clinical trial practice [6].
From the probability point of view, the statistics are not appropriately defined. ω is defined with 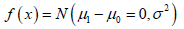 and θ is defined with
and θ is defined with 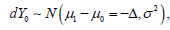 although they are properly defined respectively, they are associated with different statistical measures. Any analysis associated with different measures will be meaningless.
although they are properly defined respectively, they are associated with different statistical measures. Any analysis associated with different measures will be meaningless.
The control of the statistical error
Any CI based clinical trial design is always associated with the type I and type II error control, but the two types of the error control were defined with respect to the different statistical distributions. In a NI trial, the distribution associated with the null hypothesis 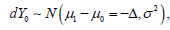 and for the alternative hypothesis, the associated distribution is
and for the alternative hypothesis, the associated distribution is 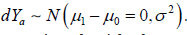 Similarly, in a SUP trial, the distribution associated with the null hypothesis is
Similarly, in a SUP trial, the distribution associated with the null hypothesis is 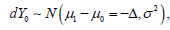 and the distribution associated with the alternative hypothesis is
and the distribution associated with the alternative hypothesis is 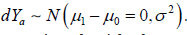
Obviously, the type I and type II error controls are with respect to the different probability measures, and combination of the two type of the errors is against the basic probability axiomatic system. More specifically, for a CI based NI trial, the type I error is defined as 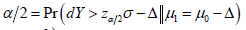 which is assessed by
which is assessed by 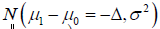 ANd the power is defined as
ANd the power is defined as 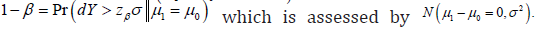 Needless to say, the power equals 1.β− The control of the type I and type II error could not be accurate at the same time. More likely, neither control is accurate.
Needless to say, the power equals 1.β− The control of the type I and type II error could not be accurate at the same time. More likely, neither control is accurate.
The proper definition of the statistical distribution
In a CI based NI trial, define event 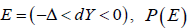 not properly defined. Similarly, for a CI based SUP trial, define event
not properly defined. Similarly, for a CI based SUP trial, define event 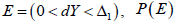 is also not properly defined. The key is that for any ,dYE∈ it is not clear which P is used to evaluate
is also not properly defined. The key is that for any ,dYE∈ it is not clear which P is used to evaluate 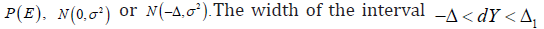 can be controlled through the choice of Δ>0 and Δ>10, but the crucial debate concentrates in this interval.
can be controlled through the choice of Δ>0 and Δ>10, but the crucial debate concentrates in this interval.
The flaw in definition
Parallel to a NI trial, the hypothesis for a SUP trial is set as
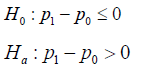
To test the hypothesis, “in most cases, the test for a treatment effect corresponds to showing that the lower bound of the one-sided 97.5% confidence interval” for 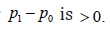
It is noted that it is not enough to provide an accurate definition for superiority. In fact, 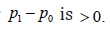 is a logical statement. In logic, a statement is either a meaningful declarative sentence that is either true or false, or that which a true or false declarative sentence asserts. The treatment effect shown through a confidence interval approach does not meet the requirement for an assertion. The width of the CI depends upon the sample size, and the lower bound of the CI less than 0 does not mean that there is no treatment effect. On the other hand, following the FDA convention in testing the NI hypothesis, when the null hypothesis is rejected, the conservative way to make a claim is that the SM is superior to AC by 0. In fact, superior by 0 include the possibility that SM is not superior to AC at all [7].
is a logical statement. In logic, a statement is either a meaningful declarative sentence that is either true or false, or that which a true or false declarative sentence asserts. The treatment effect shown through a confidence interval approach does not meet the requirement for an assertion. The width of the CI depends upon the sample size, and the lower bound of the CI less than 0 does not mean that there is no treatment effect. On the other hand, following the FDA convention in testing the NI hypothesis, when the null hypothesis is rejected, the conservative way to make a claim is that the SM is superior to AC by 0. In fact, superior by 0 include the possibility that SM is not superior to AC at all [7].
A confidence interval provides two pieces of information, a fact and the confidence. The two are correlated, but they are independent. In a NI trial, the low end of the confidence interval above the non-inferiority margin (−Δ) does not provide information of the fact, in the other words, it does not mean that there is no any inferiority. The claimed noninferiority is in fact a limited inferiority. p1-p0>-Δ provides a confidence only to the fact of this limited inferiority. It is a central debating point on the current practice.
Model Based Clinical Trial Design
The model based clinical trial design is summarized in (1) and (2), where (1) discusses the strict outcomes and (2) discusses the generalized outcomes.
Study hypothesis setup
Within a model basend clinical trial, for either a NI study or a SUP study, the study hypothesis has the same form 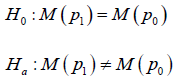
W here M represents the statistical distribution to characterize the efficacy of SM or AC. M is used in both sides implies that both SM and AC are assessed by the same distribution. The only difference is the mapping between the trial outcome and the trial conclusions. For each trial, there are three possible outcomes, EQ implies 0H is confirmed, or say aH is rejected. SUP implies aH is confirmed and 10.pp− INF implies aH is confirmed and 10.pp< Naturally, NI implies EQ or SUP conclusion.
The formulation of the model
We will consider the strict outcomes first. With Bernoulli model for each subject, the probability mass function (p.m.f.) can be written as
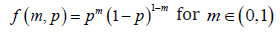
Where m=1 represents a cure, and m=0 represents a failure, for n subjects, the likelihood function can be written as
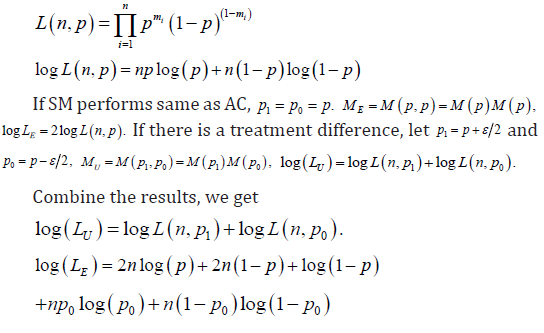
The generalized outcomes
When the generalized outcomes are considered, there are two sets of the trial hypotheses under consideration. Along with a pre-specified ,Dc based on M+ model, the trial hypothesis is

Compared with the strict model, the only difference is the definition of 1p and 0.p When M+ model is considered, 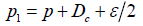 is considered to be the correct model, otherwise, the correct model is .UM Compared with the conventional analysis, the 2χ distribution is the only statistical model involved in the statistical inference, there is no second distribution used.
is considered to be the correct model, otherwise, the correct model is .UM Compared with the conventional analysis, the 2χ distribution is the only statistical model involved in the statistical inference, there is no second distribution used.
The control of the statistical error
The model based clinical trial does not consider the type I and type II statistical errors, since they are defined with different statistical distributions. But, any statistical analysis is always associated with two types of statistical error, the system error and the random error. The conventional clinical trial practice does not distinguish the two. The model based trial (1) introduced two important limitations for the error control, constant MCID ()0Dc≥and statistical MCID ()0.sD> Between the two, Dc controls the system error and sD controls the random error
It is noted that the rejection of the null implies the confirmation of the alternative and vice versa. There are two levels for a trial execution, confirmed or unconfirmed. For a given ,sD if ,sdYD< the trial result is confirmed, otherwise it is unconfirmed. Only the confirmed trial result can be considered as the trial final conclusion.
The choice of Dc has impact on the statistical model used in inference, more specifically, it is related to the mean of the random variable. The choice of sD has only impact on the accuracy of the parameter estimation. The width of the CI has integrated both Dc and sDinto one control, it does not distinguish the system and random errors.
The control of the random error
To decide which model between EM and UM to be the correct model, it needs to get a solution of the following equation.
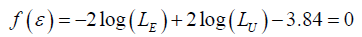
The solution to the equation, *,ε named as the minimum detectable difference (MDD), will be the largest magnitude of ε under which EM is considered to be the correct model. *ε with different p and n are summarized in the Table 1.
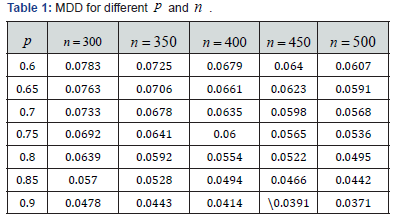
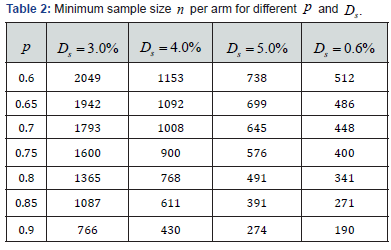
Defined the statistical MCID as ,sD to meet the requirement of *.sDε< the minimum sample size needed for different p and sD are summarized in the Table 2.
Seen from the Table 1, the higher the p and the larger the ,n the smaller the MDD. Also seen from table 2, the lower the p and the lower the ,sD the higher the .n the smaller the MDD. Also seen from Table 2, the lower the p and the lower the ,sD the higher the .n The linkage among ,,spnD and *ε is the key for the adaptive property (1). During the trial design, the actual p could not be accurately predicted. As a safeguard practice, the sample size should be higher than the minimum. Since the algorithm has an asymptotic property, the increase of the sample size will not affect the trial conclusion, it is a key difference of model based trial from the conventional CI based trial.
In the clinical trial practice, the confirmed SUP conclusion requires that 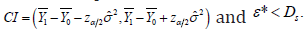 The confirmed conclusion of EQ requires that
The confirmed conclusion of EQ requires that  As discussed before,
As discussed before, 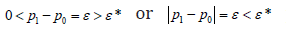 ppεε−=< provides a statement regarding a fact, and *sDε< provides the confidence. A unconfirmed conclusion will not be used as the trial final conclusion, but it provides an important guidance for the trial execution such as the interim analysis.
ppεε−=< provides a statement regarding a fact, and *sDε< provides the confidence. A unconfirmed conclusion will not be used as the trial final conclusion, but it provides an important guidance for the trial execution such as the interim analysis.
Comparison of the two strategies
Interpretation of NI and SUP
For CI based trial, guidance (4) has claimed that the NI is a misnomer, as guaranteeing that the test drug is not any (even a little) less effective than the control can only be demonstrated by showing that the test drug is superior. What noninferiority trials seek to show is that any difference between the two treatments is small enough to allow a conclusion that the new drug has at least some effect or, in many cases, an effect that is not too much smaller than the active control.
The CI based NI trial concentrated on 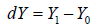 with a model
with a model 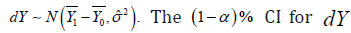 can be written as
can be written as  and the upper bound of CI above 0 will be the criteria to reject the NI null hypothesis, which implies 10.μμ−>−Δ In fact, a positive outcome of the NI trial implies that dY came from a distribution
and the upper bound of CI above 0 will be the criteria to reject the NI null hypothesis, which implies 10.μμ−>−Δ In fact, a positive outcome of the NI trial implies that dY came from a distribution 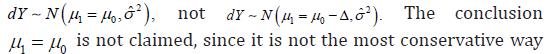 to present the trial result.μ1-μ0≥−Δ is considered to be a conservative conclusion, but it is based on a rejected statistical model. If a statistical model is considered false, any conclusion derived from the statistical model could not be considered as a truth. As previously discussed, a statement regarding a fact does not need to be either conservative or aggressive, it should stay on a neutral viewpoint. In the other words, to characterize a random variable, the mean of the distribution should be used, not the end of the confidence interval.
to present the trial result.μ1-μ0≥−Δ is considered to be a conservative conclusion, but it is based on a rejected statistical model. If a statistical model is considered false, any conclusion derived from the statistical model could not be considered as a truth. As previously discussed, a statement regarding a fact does not need to be either conservative or aggressive, it should stay on a neutral viewpoint. In the other words, to characterize a random variable, the mean of the distribution should be used, not the end of the confidence interval.
The key question the guidance (4) did not answer is how to define “small enough”. For example, with 0.10,Δ= if 0.09dY= can be considered small enough? The guidance is not able to provide a definite answer.
Unification of SUP and NI trials
In CI based trial design, SUP and NI trial are defined on different statistical distributions. Although there is a guidance (3) for the switching from NI to SUP trial, the switching is not strictly on the statistical analysis foundation and the switching from SUP to NI is impossible. In the model based trial design, both SUP and NI trial are on exactly same set of statistical analysis based on the same statistical model, and the difference only exist in the final stage of interpreting the trial result.
Statistical model for inference
There is a significant difference in the choice of the statistical model for inference. In the CI based trial design, there are always two distinct statistical models involved, which automatically introduced two statistical measures in the same analysis. In the model based clinical trial design, no matter SM and AC are same or not, all the statistical inference is based on a single 2χ distribution. All the statistical inference have been unified into the same statistical structure. In a hypothesis test, the alternative hypothesis has to be strictly complementary to the null hypothesis. Then, the rejection of the null hypothesis is considered to be the proof that the alternative hypothesis to be true. If there is a gap between the null hypothesis and alternative hypothesis set up, the foundation of the hypothesis test is destroyed. Return to the CI based NI trial, the success of the trial is to show that 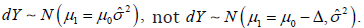 In the other words, type I error control only is not enough to show the trial conclusion, since
In the other words, type I error control only is not enough to show the trial conclusion, since 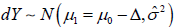 is a rejected model. To show a successful trial conclusion, it is more important to show the type II error control, but the CI based trial generally lack the information in trial conclusion. In contrast, the model based trial design unified the type I and type II error controls, the statistical inference is based on a sole statistical distribution, or say the same model. In the sense, the statistical hypothesis test is more accurate.
is a rejected model. To show a successful trial conclusion, it is more important to show the type II error control, but the CI based trial generally lack the information in trial conclusion. In contrast, the model based trial design unified the type I and type II error controls, the statistical inference is based on a sole statistical distribution, or say the same model. In the sense, the statistical hypothesis test is more accurate.
Confidence of statistical inference
In CI based trial design, the confidence of the parameter estimates were controlled by the width of CI. Since the width of CI is the function of the trial sample size, the change of the sample size has a direct impact on the trial conclusion. On the other hand, the CI based trial design does not make difference between the system error and the random error, and it does not clarify the size of the system error. When the model based trial design is considered, if there is an allowed inferiority specified, it will be controlled by the constant MCID ().Dc It is discussed extensively in (3), which is related to a shifted model.
Asymptotic and adaptive properties
During the discussion of the statistical properties of parameter estimation, the asymptotic and self-adaptive properties of the parameter estimation are important properties to the analysis. The asymptotic property refers to the property that the random error will get smaller along with the increase of the sample size. More importantly, when the sample size is beyond the minimum requirement, the conclusion of the trial will not change along with the increase of the sample size. As discussed in (1), this property can be shown through 
The self-adaptive property refers to the property that the trial conclusion does not depends upon the change in trial parameters. Any clinical trial has to have certain initial trial parameter assumptions, the trial conclusions can be different due to these assumptions. If the trial conclusion is sensitive to these assumptions, the trial conclusion can be challenged. This property is shown through the function of *,ε ,n and ,p it is also discussed in (1). Besides, the likelihood ratio test requires that ˆp has to be the maximum likelihood estimate of ,p it is also shown in (1).
The CI based clinical trial design does not first two properties, so the trial practice adopted some additional limitations not from the statistical analysis principle. For example, the trial sponsor is not allowed to increase the sample size arbitrarily. The first two properties are advantages of the model based clinical trial compared to the CI based clinical trial design methodology.
The foundation of the model based clinical trial
In this manuscript, the importance of the likelihood ratio test is stressed. In the statistical analysis, the Neyman-Pearson lemma, (5), has shown that the likelihood ratio test is the uniformly most powerful statistical test among all the statistical hypothesis test. On the other hand, it is a natural link between the conventional statistical analysis and the model based statistical analysis. There is a school of statisticians concentrated on the model based statistical analysis, such as information theoretical model selection methodologies. These methodologies are built on the same foundations of the statistical axiom systems, but they were developed in different path. For example, the basic philosophy in model selection is to choose a best model out of a large model selection, the best model does not guarantee to be a “good” model, there is no concept on the confidence. It is the reason that the model selection methodology has not been widely used in the clinical trial practice.
To introduce the model selection methodology into the clinical trial analysis, it is necessary to link the model based analysis and the conventional analysis through a bridge. Strictly speaking, the likelihood ratio test and the associated 2χ distribution can only be vaguely called the model based statistical analysis, but it provides a natural common ground for both conventional and the model based analyses. In the other words, before the model based analysis is fully explored, the purpose of this manuscript is to built a bridge to link the two. More general model based clinical trial design methodologies will be introduced in a follow-up manuscript.
Conclusion
With CI based trial design, the NI trial is not able to show the NI in common sense. Similarly, the SUP trial is not able show SUP in common sense. When a SUP is claimed, a natural question is by how much the SM is superior to AC. It will lead to the conservative SUP trial design, since the strict SUP can only show that SM is superior to AC by 0. The key is that the definition of NI and SUP have not been accurately addressed, and its statistical inference implied many approximations in violation to the statistical analysis axiom systems. This manuscript introduced the basic idea of model based clinical trial design through the likelihood ratio test (LRT), but LRT is not the only tool for model based clinical trial design. The important of LRT is not only the ideal statistical properties such as the asymptotic and self-adaptive properties as the manuscript described, as well as the Neyman-Pearson lemma pointed out, it serves a key bridge between the general model based statistical analysis with the conventional statistical analysis. It will serve as a foundation for further discussion.
References
- Chen X (2013) A non-inferiority trial design without need for a conventional margin. Journal of Mathematics and System Science 3: 47-54
- Chen X (2013) The generalized clinical trial outcomes. Journal of Mathematics and System Science 3: 167-172.
- EMA (2000) Points to consider on Switching between superiority and non-inferiority.
- FDA (2016) Non-Inferiority Clinical Trials to Establish Effectiveness.
- Hogg Craig (2004) Introduction to Mathematical Statistics, Pearson Education.
- Kolmogorov AN (1933) Grundbegriffe der Wahrscheinlichkeitrechnung, Ergebnisse Der Mathematik; translated as Foundations of Probability. New York: Chelsea Publishing Company, USA
- McCullagh P (2002) What is a statistical model. The Annals of Statistics 30(5): 1225-1310






























