Research Article

Performance of Partial Least Squares + Linear Discriminant Analysis versus k-Nearest Neighbors for Validation Set Classification of Cancer DNA Microarray Data

Joseph L Hagan¹* and Sudesh K Srivastav²

¹ Department of Pediatrics–Neonatology, Baylor College of Medicine, United States

²School of Public Health and Tropical Medicine, Tulane University, United States

Submission: November 16, 2018; Published: January 04, 2019

*Corresponding author: Joseph L Hagan, ScD. Assistant Professor, Department of Pediatrics–Neonatology, Baylor College of Medicine, Texas Children’s Hospital, United States

How to cite this article: Joseph L H, Sudesh K S. Performance of Partial Least Squares + Linear Discriminant Analysis versus k-Nearest Neighbors for Validation Set Classification of Cancer DNA Microarray Data. Biostat Biometrics Open Acc J. 2019; 9(1): 555752. DOI: 10.19080/BBOAJ.2019.09.555752

Abstract

The purpose of this study is to systematically compare the performance of Partial Least Squares + Linear Discriminant Analysis (PLS+LDA) with k-nearest neighbors (KNN) for validation set classification of cancer DNA microarray data. Nine different cancer microarray datasets were analyzed to obtain the optimal PLS+LDA and KNN classifiers, which were then compared in terms of the misclassification rates in the validation set. Additionally, the Singh prostate cancer dataset was resampled via bootstrapping for simulation studies of the effect of class imbalance and sample size on the two supervised learning methods’ misclassification rates. Across the 9 cancer datasets, PLS+LDA had a significantly lower validation set misclassification rate than KNN after controlling for classifier evaluation method (p=0.034). After controlling for supervised learning method, the estimated validation set misclassification rate of classifiers evaluated via bootstrap sampling was 2.9% higher (p<0.001) than leave-one-out cross-validation (LOOCV), and 1.6% higher than 5-fold cross-validation (p=0.004).

In the simulation study of the effect of class imbalance, the KNN classifiers’ misclassification rate decreased significantly with increasing class imbalance (r = -0.991, p = 0.001) while the misclassification rate of PLS+LDA classifiers was insensitive to class imbalance (r = 0.013, p = 0.984). In the simulation study of the effect of sample size, the misclassification rates of both PLS+LDA (r= - 0.921, p<0.001) and KNN (r= -0.898, p=0.001) declined with increasing sample size, but the PLS+LDA misclassification rate was consistently lower than KNN across the simulated sample sizes (p<0.001). The PLS+LDA supervised learning method is preferred over KNN for classification of cancer DNA microarray data due to a generally lower misclassification rate and less sensitivity to learning set class proportions. Bootstrapping and 5-fold CV are better suited for classifier evaluation and selection than and LOOCV

Keywords: Partial least squares; Linear discriminant analysis; k-nearest neighbors; Cancer DNA microarray data

Abbrevations: PLS+LDA: Partial Least Squares + Linear Discriminant Analysis; KNN: k-Nearest Neighbors; m-fold CV: m-Fold Cross-Validation; LOOCV: Leave-One-Out Cross-Validation; SAM: Significance Analysis of Microarrays; SMOTE: Synthetic Minority Over-Sampling Technique

Introduction

Supervised learning is a broad category of techniques used to develop a classification rule to differentiate the class of observations (tissue samples in this study) when the true class of each observation in the data set is known. The classification rule can then be used to predict the class of a new mystery specimen. Such methods can be employed in any situation for which it is desirable to predict the phenotype of a biological sample given the sample’s gene expression data. These class prediction methods can be used to create gene expression diagnostic classifiers for cancer, which is the application of interest in this study.

For a binary response (e.g., cancerous or normal tissue), the gene expression data obtained from a microarray experiment can be represented as a gn× matrix,X, in which the g rows correspond to genes and the n columns correspond to samples, each of which are known a priori to belong to one of the two classes. The ijx value represents the (transformed and/or normalized) gene expression measurement for the ith gene in the jth sample and a vector, Y , indicates the true class membership of each sample. A classifier is a function that partitions the space of the gene expression profiles into two (for a binary outcome) disjoint and exhaustive subsets so that each of the n samples will be assigned to a predicted class.

In the context of class prediction from microarray gene expression data, traditional statistical methods (e.g., logistic regression) generally do not perform well due to the so called “curse of dimensionality” (Bellman [1]) resulting from the fact that, in microarray studies, there are often fewer than 100 observations (samples) but the number of predictors (genes) represented on a microarray chip is usually several thousand at a minimum. In most microarray studies, from a biological standpoint there will generally be only a relatively small subset of genes that contain meaningful information with regard to the class membership. Thus, for the purposes of class prediction, implementation of supervised classification techniques is usually preceded by feature selection in order to reduce the number of genes used.

Studies of statistical methods for selecting differentially expressed genes have found little overlap between the gene lists obtained from different methods. For example, Jeffery et al. [2] examined ten different feature selection methods and observed only 8% to 21% of genes in common from gene lists produced by these methods. Such a lack of agreement in gene lists is worrisome if the purpose of a study is to identify genes for further investigation (e.g., genes to serve as targets for therapeutic agents, etc.). But when the purpose is to develop an algorithm for class prediction, Shi et al. [3] observed only a minor contribution of feature selection method to prediction performance. The minor role played by choice of feature selection method can be partly explained by the finding (e.g., Boutros et al. [4]) that on the same dataset, good predictive performance can be achieved using different gene lists with very little overlap.

There are many feature selection methods available, four of which will be considered in this study: Student’s t-test for two independent samples, Welch’s t-test, the Wilcoxon rank-sum test (a.k.a., Mann-Whitney U test or the Mann-Whitney-Wilcoxon test), and Significance Analysis of Microarrays (SAM) (Tusher et al. [5]). The gene lists used in this study will be generated from these four methods by ranking genes in terms of their significance based on the test statistics. Five different gene list sizes will be used for class prediction. So as to avoid optimistically biased estimation of the misclassification rates, feature selection will be performed using only data from the training set (a.k.a., learning set), and evaluation will be subsequently performed on the validation set (Ambroise and McLachlan [6]). Note that for datasets with more than two classes, a “one-vs.-rest” scheme, as implemented in the GeneSelection function in Bioconductor’s CMA library, will be used for feature selection. PLS+LDA and KNN are two commonly used supervised learning methods in cancer genetics studies that will be examined in this study.

k-nearest neighbors (KNN)

The class of each sample in the validation set is predicted using information from the k “nearest” samples in the training set. A class prediction is made for a test sample based on a majority vote of its neighbors, with the test sample class being predicted as the class most common among its k nearest neighbors. The number of nearest neighbors, k, is a positive integer which is either specified a priori (Simon et al. [7]), or k can be selected via parameter tuning as discussed below. For binary classification, choosing an odd number for k is desirable in order to avoid voting ties.

The nearest neighbors are the samples in the training set with the gene expression profile most similar to the test sample. That is, the closest k samples from the training set are selected to be those with the smallest distance from the sample whose class is being predicted (Figure 1). There are a number of possible distance measures that can be used (e.g., one minus the correlation coefficient, Mahalanobois distance, or Euclidean distance). Euclidean distance is the distance metric used for the implementation of KNN in this study (classifier = ‘knnCMA’ in the Bioconductor CMA library). For two samples, 1x and 2,x with expression levels measured for each of g genes, the Euclidean distance across all genes can be defined as

To implement the KNN algorithm due to Fix & Hodges [8], in turn for each sample in the validation set:

(i) Find the k closest samples in the learning set, and

(ii) Predict the class of the test sample by choosing the class that is most common among those k neighbors.

In this study KNN will be implemented with the value of k tuned via internal 3-fold cross-validation over the parameter space k = 1, 3 and 5. When the value of k is selected via internal cross-validation, the nearest neighbors algorithm is performed on the learning set only. To begin the internal cross-validation, the samples in the learning set are randomly partitioned into three internal folds, one of which is initially designated as the internal validation set with samples from the other two folds used for the internal learning set. Each of the values of k under consideration is used to construct the classifier and predict the class of each of the samples in the internal validation set. Each of the three internal folds are in turn treated as the internal validation set for a single internal CV iteration. The value of k yielding the lowest misclassification rate in internal cross-validation is then used to construct the KNN classifier for prediction on the original (external) validation set. The predicted class for each validation set sample is then compared to the test sample’s true class so that the misclassification rate can be computed. Note that this whole process represents a single external cross-validation iteration. Then a new learning set / validation set partition is generated and the entire process is repeated for B iterations (B =200 for this study).

Partial least squares + linear discriminant analysis (PLS+LDA)

Partial least squares (PLS) is a dimension reduction technique that finds the “components” (weighted linear combinations of genes) that maximize the covariance with Y (an nn× matrix indicating the class membership of each sample). The PLS regression model is

where the nr× matrix of components (),rg< ,T is a linear combination of the original gene expression matrix, TX (with dimensions ng×), and where P (with dimensions gr×) and Q (with dimensions nr× ) are “loading” matrices of coefficients, with E (having dimensions ng× ) and F (having dimensions nn× ) being matrices of the normal independent identically distributed random errors.

The number of components, ,r is chosen by the analyst. In this study, PLS+LDA will be implemented using either 2 components or 3 components as determined by internal 3-fold cross-validation (as described for KNN above). The matrix of components, T, represents a linear transformation of TX,T=TXW, where W is a gr× matrix of weights. The columns of W and T can be represented by 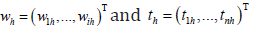respectively for h = 1,…, r with W chosen so as to maximize the squared sample covariance, ˆCov (,)YT, under the condition that the components are uncorrelated (Boulesteix & Strimmer [9]). For PLS+LDA as implemented in this study (classifier = ‘pls_ldaCMA’ in Bioconductor’s CMA library), the nr× matrix of components, T will be used as the predictors in linear discriminant analysis (LDA, described below). Either two or three components (the “ncomp” parameter) will be used with the choice determined via internal CV as described above for KNN.

Let (1)t and (2)t represent the sample mean of the two classes’ PLS components, and let represent the components’ estimated covariance matrices. Fisher’s LDA finds the linear projections of the components that most effectively distinguishes between the classes. The vector JT of PLS components for the jth sample is reduced to a scalar by a linear transformation:

where the v values are component-specific weights chosen to maximize class discrimination of samples in the learning set.

Fisher [10] defined maximal discrimination as the linear combination resulting in the largest ratio of the absolute difference in class means to within class variability. The same v values are used for all n samples. For the vector of weights,, maximal discrimination occurs when . A test sample (j*) from the validation set with the vector components Tj* will be assigned the predicted class 1 if (1)(2)*()/2jtt⋅>⋅+VTV. Otherwise the predicted class will be 2.

Classifier evaluation

Validation is needed to evaluate the accuracy of a classifier’s predictions. In order to avoid overly optimistic assessments of a classifier’s predictive ability, validation should be performed on samples other than those used to construct the classifier. This is accomplished by building the classifier, including any preliminary feature selection, using only information from a training set (a.k.a. learning set) of data, and subsequently evaluating the classifier using a validation set of data comprised of test samples which were not included in the training set. This type of assessment in which a portion of the original dataset is set aside for evaluation purposes is referred to as cross-validation.

In practice, the parameters of a classifier are tuned via cross-validation in the training set. The classifier with the best performance in validation set cross-validation is then “frozen” and used to predict the class of future mystery samples. Although numerous classifier evaluation methods exist, the three used in the present study are bootstrap sampling, m-fold cross-validation (m-fold CV) and leave-one-out cross-validation (LOOCV). The misclassification rate (i.e., the proportion of misclassified samples in the validation set) is the performance measure used in this study to assess the predictive ability of the classifiers.

Bootstrap sampling

From a full dataset composed of n samples, n samples are randomly chosen with replacement for inclusion in the training set. The validation set is comprised of samples which were not chosen for the training set, so the validation set in each bootstrap iteration will have a variable number of samples. For each of the B bootstrap iterations, the classifier is constructed from the training set data and then applied to each sample in the validation set. The misclassification rate is computed as the mean proportion of samples misclassified per iteration, across the B iterations. Stratified bootstrap sampling was used to maintain the same class proportions in the training set of each iteration as the original dataset class proportions. Two-hundred bootstrap iterations were used for analysis of the experimental datasets.

m-Fold cross-validation (m-fold CV)

The n samples in the original full dataset are randomly separated into m non-overlapping groups of equal size. (When nm is not an integer, the number of samples allocated to one or more of the folds will have a sample size difference of one from the other fold(s), in order to have a total of n predictions across the m folds.) Each of the m folds are in turn used as the validation set while the other 1m−folds are combined to form the training set. During the entire m-fold CV procedure, a prediction is made for each of the n samples in the full dataset. An m-fold CV iteration is complete after each of the m folds has been treated as the validation set. Then the next iteration begins with a new random partitioning of the m folds. The misclassification rate is computed as the mean proportion of samples misclassified per iteration. Stratified 5-fold CV was implemented in the present study to maintain the class proportions of the original dataset in each of the m folds. Two-hundred m-fold CV iterations were be used for analysis of the nine experimental datasets.

Leave-one-out cross-validation (LOOCV)

For LOOCV, each of the individual n samples in the full dataset are, one-at-a-time, treated as the validation set, with the remaining 1n− samples used to form the training set. Note that LOOCV is merely a special case of m-fold CV where . mn= Also note that the LOOCV sampling partitions of the training set and validation set are completely deterministic since each individual sample in the dataset is sequentially treated as the validation set, and the remaining samples comprise the training set. On the other hand, the bootstrap samples and the selection of the samples comprising the folds of the 5-fold CV learning and validation sets are randomly generated (not deterministic).

Study objective

This study compares PLS+LDA and KNN classifiers for cancer microarray data and examines the effect of classifier evaluation method. The effects of class imbalance and sample size are also investigated in a simulation study. Characteristics of the classifiers such as the best gene selection method and number of genes used in the optimized classifier are also described.

Methods

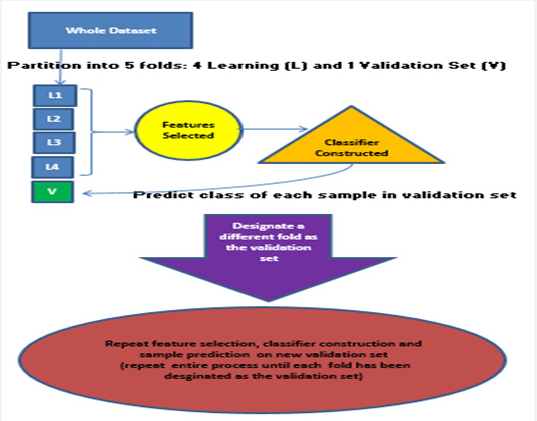
Experimental dataset workflow

The workflow for both supervised learning methods’ classifiers on each experimental dataset is summarized in Table 1 and one 5-fold CV iteration is depicted schematically in Figure 2. The study workflow is designed to provide a comparison of the classifiers by analyzing nine real cancer microarray datasets. Classifiers constructed from the nine experimentally derived publicly available microarray datasets from previously published studies will be evaluated via three classifier evaluation schema (LOOCV, 5-fold CV with 200 iterations and Bootstrap sampling with 200 iterations), using four gene selection methods (the t-test, Welch test, Wilcoxon rank-sum test, and SAM) used to select gene lists of five sizes (20, 50, 100, 200 and 500 genes). Publicly available cancer microarray datasets that had already been pre-processed and normalized were chosen. Table 2 summarizes the nine experimental datasets analyzed and descriptions of these datasets are given in Appendix 1 [11-19].

PLS+LDA: Partial Least Squares + Linear Discriminant Analysis, KNN: k-nearest neighbors, m-fold CV: m-fold cross-validation, LOOCV: leave-one-out cross-validation, SAM: Significance Analysis of Microarrays.

Analysis of experimental data results

A mixed effects linear model with a compound symmetry covariance structure was used to investigate the effect of supervised learning method (KNN versus PLS+LDA) on misclassification rate after controlling for validation method (5-fold CV, LOOCV and bootstrap) while accommodating the repeated misclassification rates arising from the same dataset via different validation methods. Initially a “saturated” regression model was fit as specified below:

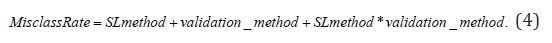
If the supervised learning method-by-validation method interaction term was not significant (α=0.05) then it was removed and the regression model was refit using only the supervised learning method and classifier evaluation method main effects, as specified below:

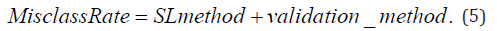
The number of genes selected for KNN vs. PLS+LDA classifiers was compared in a similar way using a mixed effects linear model.

Simulated data methods

Simulation studies were undertaken to examine the effects of sample size and imbalance in the number of samples per class on predictive performance. The simulations were based on the experimental data from the Singh et al. [14] study. The original Singh dataset contained gene expression levels measured on 52 prostate cancer tumor samples and 50 normal prostate tissue samples. For the sake of simplicity, for the simulation studies we considered 100% of the dataset to be 50 cases (instead of 52 cases as were present in the original experimental dataset) and 50 controls in the learning set. For the simulation study investigating the effect of sample size, the proportion of samples from each class in the learning set in the resampled datasets were reduced from 100% to 90%, 80%, 70%, 60%, 50%, 40%, 30%, 20%, and 10% of the original sample size. (In other words, the number of cases in each learning set random sample was 45, 40, 35, 30, 25, 20, 15, 10, and 5.) From the original Singh [14] experimental dataset, a learning set of the desired sample size and class proportion was selected with replacement. Observations that were not selected for the learning set comprised the validation set. Classifiers were trained using the same workflow previously described for the experimental data with 200 total bootstrap iterations performed at each sample size and class proportion examined.

For the simulation study investigating the effect of class imbalance, the Cancer:Control class ratios generated in the bootstrap resampled learning sets were 10%:90%, 20%:80%, 30%:70%, 40%:60%, 50%:50% 60%:40%, 70%:30%, 80%:20% and 90%:10%. For each of the nine class ratios, 200 simulated learning sets were generated and analyzed using the same workflow described above for the experimentally derived datasets.

For each dataset generated with the specified proportion of samples represented by controls for the class imbalance simulation study, the tuned classifier yielding the lowest mean misclassification rate across the 200 simulated datasets among all gene selection methods and gene list sizes was chosen as the classifier to represent the supervised learning method. Similarly, for each dataset of specified size in the sample size simulation study, the tuned classifier yielding the lowest mean misclassification rate across the 200 simulated datasets among all gene selection methods and gene list sizes was chosen. For the class imbalance simulation study, “class imbalance” was defined as the absolute value of the difference between 50% and the percentage of samples represented by cases (i.e., imbalance = |bootstrap sampled proportion cases – 0.5|). The rationale was to examine the effect on supervised learning methods’ misclassification rate as the ratio of cases to controls departed from 50%.

Pearson’s correlation was used to examine the associations of class imbalance and sample size with misclassification rate, separately for PLS+LDA and KNN classifiers. Pearson’s correlation coefficients measuring the associations of class imbalance and sample size with misclassification rate were compared for PLS+LDA versus KNN classifiers via the method for comparing “related dependent” correlation coefficients due to Steiger [20] using the SAS code provided by Looney & Hagan [21]. The correlation coefficients are considered “dependent” because they are computed using the same simulated data. The correlation coefficients are “related” because they share a common variable, namely “class imbalance” in the proportion simulation study, and “sample size” in the sample size simulation study. Correlations of these two simulated parameters with the two supervised learning methods’ misclassification rates are tested for equivalence under the null hypothesis. Additionally, multiple linear regression analysis was used to compare the two supervised learning methods’ misclassification rates after controlling for class imbalance or sample size.

Results

Experimental datasets

When analyzing the experimental dataset misclassification rates initially using a “saturated” mixed effects linear regression model, the interaction between supervised learning method and classifier evaluation method was not significant (p = 0.919) indicating that the relative performance of the two supervised learning methods did not depend on which classifier evaluation method was used. Thus, the interaction term was removed and the regression model was refit using only the main effects of supervised learning method and classifier evaluation method.

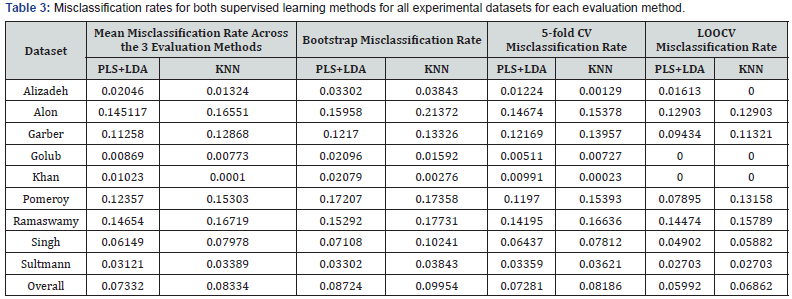
PLS+LDA: Partial Least Squares + Linear Discriminant Analysis, KNN: k-nearest neighbors, m-fold CV: m-fold cross-validation, LOOCV: leave-one-out cross-validation.

Looking across all 9 experimental datasets, after controlling for classifier evaluation method, the estimated validation set misclassification rate of PLS+LDA was 1.0% lower in absolute terms than KNN (p=0.034). The mean misclassification rate across the three evaluation methods was lower for PLS+LDA for six of the 9 cancer datasets. In relative terms, the overall misclassification rate for PLS+LDA was (1-(0.07332/0.08334)) x 100% = 12.0% lower than for KNN (Table 3). Regarding validation method, after controlling for the supervised learning method, LOOCV had an estimated misclassification rate that was 2.9% lower than the bootstrap method (p<0.001), and 5-fold CV had an estimated misclassification rate that was 1.6% lower than the bootstrap method (p=0.004), while the estimated misclassification rate of LOOCV was 1.3% lower than 5-fold CV (p=0.014).

In the optimal classifiers for both supervised learning methods, the t-test was the most commonly used method for selecting differentially expressed genes, and the smallest gene list sizes (number of genes=20) was most commonly used (Appendix 2). The gene list size of optimal classifiers did not differ significantly across the three classifier evaluation methods after controlling for supervised learning method (p=0.775), nor did the gene list size differ between the two supervised learning methods after controlling for classifier evaluation method (p=0.706).

Simulation study

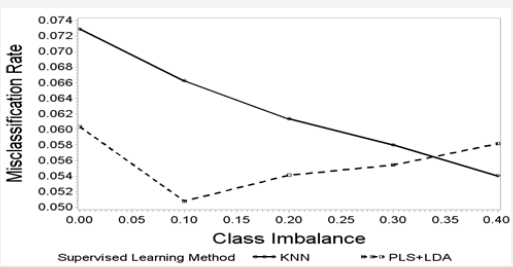
Looking across the simulated class proportions, for KNN classifiers, greater class imbalance was associated with a significantly lower misclassification rate (r = -0.991, p = 0.001) but the misclassification rate of PLS+LDA classifiers was not associated with class imbalance (r = 0.013, p = 0.984). The magnitude of the correlation of the KNN classifier misclassification rate with class imbalance was significantly greater than PLS+LDA classifier (p=0.007). The misclassification rate of KNN classifiers was highest (7.3%) when the classes were balanced and decreased steadily as the class imbalance increased, reaching a minimum misclassification rate of 5.4% at the maximum class imbalance; whereas the misclassification rate of PLS+LDA classifiers varied much less (from 5.1% to 6.0%) and the misclassification rate was not monotonically associated with class imbalance (Figure 3).

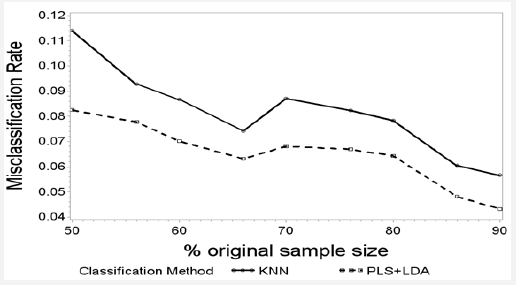
The misclassification rates of both PLS+LDA (r= -0.921, p<0.001) and KNN (r= -0.898, p=0.001) declined steadily with increasing sample size (Figure 4). The misclassification rate of PLS+LDA was consistently lower than the misclassification rate of KNN across all sample sizes, with a predicted misclassification rate that was an estimated 1.7% lower in absolute terms than the misclassification rate of KNN, after controlling for the sample size (p<0.001). For both KNN (r=0.085, p = 0.829) and PLS+LDA (r=0.194, p = 0.617), the number of genes used in the classifier was not significantly associated with the simulated sample size. For both KNN (r= -0.294, p = 0.442) and PLS+LDA (r= -0.546, p = 0.128), the number of genes used was not significantly associated with class imbalance.

Discussion

Overall, PLS+LDA classifiers performed better than KNN classifiers in this study. In the nine experimental cancer datasets, PLS+LDA had a significantly lower validation set misclassification rate than KNN, although this difference did not generalize across every individual cancer dataset. In simulation studies, the PLS+LDA misclassification rate was consistently lower than KNN’s in the presence of reduced sample sizes, and PLS+LDA showed less sensitivity to learning set class proportions. Both methods’ misclassification rates increased as learning set sample size decreased. No differences were observed in gene selection method or gene list sizes of the two supervised leaning methods’ classifiers. A PubMed search (11/3/2018) of “nearest neighbor”, “partial least squares” and “linear discriminant analysis” yielded 6063, 9272 and 4186 publications, respectively, which was reduced to 513, 505 and 837 when these publications were restricted to those sharing the search term “cancer”. So these supervised learning methods are commonly used in cancer research. Using PLS in conjunction with LDA as was done in this study combines two different supervised learning methods. Recently, other adaptations of PLS have been proposed for classification of high dimensional gene expression data. For example, Durif et al. [22] developed “an adaptive version of the sparse PLS for classification, called logit-SPLS, which combines iterative optimization of logistic regression and sparse PLS”. But standard PLS has also been shown to be superior to other common methods for classification of genomic data (Sun et al. [23]).

Regarding classifier evaluation method, LOOCV had a significantly lower validation set misclassification rate than 5-fold CV and bootstrap sampling. Bootstrap sampling is the better choice of evaluation for selecting between classifiers due to the relatively high validation set misclassification rate, thereby providing greater ability to discriminate between the performances of different classifiers. With LOOCV, there were numerous ties between classifiers’ misclassification rates because of the discrete number of predictions made, so LOOCV is not a suitable method of classifier evaluation for the purpose of identifying the optimal classifier.

When the goal is to assess the relative performance of different classifiers, LOOCV is not recommended due to the large potential for ties. As can be seen in in the results presented above, the misclassification rates of PLS+LDA and KNN were tied in 4 of the 9 datasets when evaluated via LOOCV, but no ties occurred for 5-fold CV or bootstrapping. The reason for so many ties is that the misclassification rate computed by LOOCV can be considered a discrete measurement, especially for datasets of small sample size, since the misclassification rate can only take values from 0 to 1 in increments of 1.

A recent systematic study of the evaluation of PLS+LDA classifiers (Rodriguez-Perez et al. [24]) noted that LOOCV is frequently used to evaluate PLS+LDA classifiers in omics research, although bootstrap and m-fold CV are preferred because these methods are not as optimistically biased as LOOCV. Interestingly. Zervakis et al. [25] claim that estimates of error rates obtained by LOOCV are “over-optimistic” but other studies claim that LOOCV provides a nearly unbiased estimate of the prediction error rate (Ambroise and McLachlan [6], Boulesteix et al. [26], Man et al. [27], Aeberhard et al. [28], Hastie et al. [29]). So there is not agreement on the accuracy of the error rate estimation of LOOCV, but its use for classifier selection is discouraged due to the common occurrence of ties in classifiers’ misclassification rates.

Similar to the present study, Jeffery et al. [2] observed a consistent decrease in classification performance when the sample size of learning sets was reduced by randomly removing pre-specified proportions of samples. In another simulation study, Popovicil et al. [30] examined classification performance on breast cancer data using two different resampling methods and came to the conclusion that “genomic predictor accuracy is determined largely by an interplay between sample size and classification difficulty” of the specific endpoint. The current study did not find a statistically significant relationship between simulated sample size or class imbalance with gene list size for either supervised leaning method. But based on trends observed in this study, we expect that a more focused simulation study designed to systematically investigate the association between class imbalance and gene list size could demonstrate a correlation.

In another simulation study that examined the effects of class imbalance and sample size by resampling a breast cancer dataset, consistent with the current study, Blagus and Lusa [31] concluded that LDA was less sensitive to class imbalance than KNN. Although the Blagus and Lusa [31] simulation study was informative, their experimental design confounded associations between sample size and class imbalance because in every instance that the class proportions changed, the sample size also changed, so the most highly imbalanced resampled datasets were also the datasets with the largest sample size. By contrast, the simulation studies presented here manipulated sample size and class imbalance independently, thereby allowing for a separate investigation of the effect of each factor.

A recent review (Haixiang et al. [32]) of statistical methods for supervised learning with class-imbalanced data found under-sampling the majority class and over-sampling the minority class to be two strategies commonly used to deal with imbalanced data. For example, Zheng et al. [33] proposed a variation of the synthetic minority over-sampling technique (SMOTE) that oversamples the minority class by creating a feature space for an artificial sample that is a stochastically weighted average of the feature space of a selected observation in the minority class and a randomly chosen nearest neighbor. Although the method performed well in the Zheng et al. [33] study, Yin & Gai [34] found that “under sampling performs better than oversampling when the dataset is largely imbalanced” in a study using 12 different datasets. Interestingly, a recent study showed that using KNN with LDA significantly improved breast cancer classification performance compared to KNN alone (Joshi and Mehta [35]). Future research to compare the performance of KNN+LDA with PLS+LDA would be interesting.

Conclusion

We recommend PLS+LDA over KNN for classification of cancer DNA microarray data. Compared to KNN, PLS+LDA has a significantly lower validation set misclassification rate, although this did not generalize across every individual cancer dataset. Additionally, the PLS+LDA misclassification rate performs better with small sample sizes and shows less sensitivity than KNN to class proportions.

Acknowledgement

We are grateful to Vladimir Morozov for his assistance with writing the R code to implement the simulation studies.

References

1. Bellman RE (1961) Adaptive Control Processes Princeton University Press, Princeton, NJ, USA.
2. Jeffery IB, Higgins DG, Culhane AC (2006) Comparison and evaluation of methods for generating differentially expressed gene lists from microarray data. BMC Bioinformatics 7: 359.
3. Shi L, Campbell G, Jones WD, Campagne F, Wen Z, et al. (2010) The MicroArray Quality Control (MAQC)-II study of common practices for the development and validation of microarray-based predictive models. Nat Biotechnol 28(8): 827-837.
4. Boutros PC1, Lau SK, Pintilie M, Liu N, Shepherd FA, et al. (2009) Prognostic gene signatures for non-small-cell lung cancer. Proc Natl Acad Sci U S A 106(8): 2824-2828.
5. Tusher VG, Tibshirani R, Chu G (2001) Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci U S A 98: 5116-5121.
6. Ambroise C and McLachlan GJ (2002) Selection bias in gene extraction on the basis of microarray gene-expression data. Proc Natl Acad Sci U S A 99(10): 6562-6566.
7. Simon R (2003) Using DNA Microarrays for Diagnostic and Prognostic Prediction. Expert Review of Molecular Diagnostics 3(5): 587-595.
8. Fix E, Hodges JL (1951) Discriminatory analysis, nonparametric discrimination: Consistency properties Technical Report 4, USAF School of Aviation Medicine, Randolph Field, Texas, USA.
9. Boulesteix AL, Strimmer K (2007) Partial Least Squares: A versatile tool for the analysis of high-dimensional genomic data. Brief Bioinform 8(1): 32-44.
10. Fisher, RA (1936) The use of multiple measurements in taxonomic problems. Annals of Eugenics 7: 179-188.
11. Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, et al. (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci U S A 96(12): 6745-6750.
12. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, et al. (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286(5439): 531-537.
13. Khan J, Wei JS, Ringnér M, Saal LH, Ladanyi M, et al. (2001) Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nature Medicine 7(6): 673-679
14. Singh D, Febbo PG, Ross K, Jackson DG, Manola J, et al. (2002) Gene expression correlates of clinical prostate cancer behavior. Cancer Cell 1(2): 203-209.
15. Sültmann H, von Heydebreck A, Huber W, Kuner R, Buness A, et al. (2005) Gene expression in kidney cancer is associated with novel tumor subtypes, cytogenetic abnormalities and metastasis formation, and patient survival. Clin Cancer Res 11(2 Pt 1): 646-655.
16. Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, et al. (2000) Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 403(6769): 503-511.
17. Garber ME, Troyanskaya OG, Schluens K, et al. (2001) Diversity of gene expression in adenocarcinoma of the lung. PNAS 98(24): 13784-13789.
18. Pomeroy SL, Tamayo P, Gaasenbeek M, Sturla LM, Angelo M, et al. (2002) Prediction of central nervous system embryonal tumor outcome based on gene expression. Nature 415(6870): 436-442.
19. Ramaswamy S, Ross KN, Lander ES, Golub TR (2003) A molecular signature of metastasis in primary solid tumors. Nature Genetics 33(1): 49-54.
20. Steiger JH (1980) Tests for Comparing Elements of a Correlation Matrix. Psychological Bulletin 87: 245-261
21. Looney SW, Hagan J (2015) Analysis of Biomarker Data: A Practical Guide. In: Hoboken(Eds), New Jersey: John Wiley and Sons, Inc. USA.
22. Durif G, Modolo L, Michaelsson J, Mold J, Lambert-Lacroix S, et al. (2018) High dimensional classification with combined adaptive sparse PLS and logistic regression. Bioinformatics 34(3): 485-493.
23. Sun H, Zhang Z, Olassege BS, Xu Z, Zhao Q, Ma P, Wang Q, Pan Y (2018) Application of partial least squares in exploring the genome selection signatures between populations. Heredity Nature.
24. Rodriguez-Perez R, Fernandez L, Santiago M (2018) Overoptimism in cross-validation when using partial least squares-discriminant analysis for omics data: a systematic study. Anal Bioanal Chem 410(23): 5981-5992.
25. Zervakis M, Blazadonakis ME, Tsiliki G, Danilatou V, Tsiknakis M, et al. (2009) Outcome prediction based on microarray analysis: a critical perspective on methods. BMC Bioinformatics 10: 53.
26. Boulesteix AL, Strobl C, Augustin T, Daumer M (2008) Evaluating microarray-based classifiers: an overview. Cancer Inform 6: 77-97.
27. Man MZ, Dyson G, Johnson K, Liao B (2004) Evaluating methods for classifying expression data. J Biopharm Stat 14(4): 1065-84.
28. Aeberhard S, De Vel OY, Coomans D H (2002) New fast algorithms for error rate-based stepwise variable selection in discriminant analysis. SIAM Journal of Scientific Computing 22: 1036-1052.
29. Hastie T, Tibshirani R, Friedman J (2009) The Elements of Statistical Learning: Data Mining, Inference and Prediction, 2nd Edition. Springer, New York, USA
30. Popovici V, Chen W, Gallas BG, Hatzis C, Shi W, et al. (2010) Effect of training-sample size and classification difficulty on the accuracy of genomic predictors. Breast Cancer Res 12(1): R5.
31. Blagus R, Lusa L (2010) Class prediction for high-dimensional class-imbalanced data. BMC Bioinformatics 11: 523.
32. Haixiang G, Li Y, Shang J, Mingyun G, Yuanyue H, et al. (2017) Learning from class-imbalanced data: Review of methods and applications. Expert Systems with Applications 73(1): 220-239.
33. Zheng Z, Cai Y, Li Y (2015) Oversampling method for imbalanced classification. Computing and Informatics 34: 1017-1037.
34. Yin H, Gai K (2015) An empirical study on preprocessing high-dimensional class-imbalanced data for classification. IEEE 17th International Conference on High Performance Computing and Communications 1314-1319.
35. Joshi A, Mehta A (2018) Analysis of k-nearest technique for breast cancer disease classification. International Journal of Recent Scientific Research 9(4): 26126-26130.