Short Communication

Further results on extended additive hazard model

Morteza Raeisi¹* and Gholamhossien Yari²

¹ Department of Statistics, Science, Research Branch Islamic Azad University, Iran

²Department of Mathematics, Iran University of Science and Technology, Iran

Submission: April 14, 2018; Published: October 23, 2018

*Corresponding author: Morteza Raeisi, Department of Statistics, Science, Research Branch Islamic Azad University, Tehran, Iran

How to cite this article: Morteza R, Gholamhossien Y. Further results on extended additive hazard model. Biostat Biometrics Open Acc J. 2018; 8(3): 555738. DOI: 10.19080/BBOAJ.2018.08.555738

Abstract

The time is an important factor for covariate variables in additive and proportional hazard model. According to this idea, Raeisi & Yari [1] introduced an extended additive hazard model and investigated some properties of this model related to reliability analysis. In this paper, we obtain further results for the model with respect to some stochastic orderings and aging properties.

Keywords: Additive hazards model; Stochastic orders; Aging properties

Mathematics Subject Classification (2010): 60E15; 60K10; 62N05

Abbrevations: AHM: Additive Hazard Model; PHM: Proportional Hazard Model; EAHM: Extended Additive Hazard Model

Introduction

One of the main purposes in survival analysis is to investigate the effects of risk factors on disease occurrence or death. When the effect of a factor under study has a multiplicative effect on the baseline hazard function, we have a proportional hazards model and an additive effect leads to an additive hazard model (AHM). Although the proportional hazard model (PHM) is mostly studied in literature sometimes it becomes important to study the AHM as well. The additive hazards model has been initiated by Aalen [2] and Aalen [3]. Nair, et al. [4] suggested a more flexible form. They considered that if *X denotes the lifetime variable in population with HR function *,h then the conditional HR function of (X*|Z=z) is given

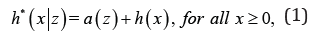
for some positive function ().azDetailed aspects of this model such as stochastic ordering and comparison with respect to many of the aging criteria have been discussed in their work. The identity of (1) aims to model the conditional hazard rate of *X given that Zz= is observed for the covariate variable, using an additive effect function of ,z on the baseline HR. Because the susceptibility to causes of failure at any given amount of the observed value of the covariate random variable Z is different over the time, it is, therefore, natural to consider an additive effect on the baseline HR as a function of both x and .z By this approach, heterogeneity of susceptibility to causes of failure of a device at any observed values of covariate Zover the time during which the device is working, is well-explained in the additive hazards model. According to this approach, Raeisi, et al. [1] introduced an extended additive hazard model (EAHM) as following

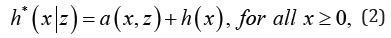
for some positive function (),axzsatisfying 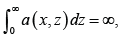for each z≥0. They investigated the model in two parts. First, they concentrated on the distribution theory of the EAHM by giving representations of the model via some reliability measure and by a number of useful illustrative examples. Then, several closure properties of the model with respect to some dependence structures, stochastic orderings and aging properties are investigated and they obtained some preservation properties of the EAHM under some stochastic orderings.

In this paper, in section 2, we present some definitions and basic properties which will be used through the paper. In section 3, we investigate the closure properties of the model with respect to some aging properties. In section 4, we discuss some conclusions.

Preliminaries

In this section, for ease of reference, we present some definitions and basic properties which will be used through the paper. First, we present definitions of some stochastic orders and aging notions. For the stochastic orders we refer to Shaked , et al. [5] and for the aging notions we refer to Lai, et al. [6] and Barlow, et al. [7]. Through this paper X and Y are two nonnegative random variables with distribution functions F and G, survival functions F=1-F and G=1-G density functions f and g and HR functions 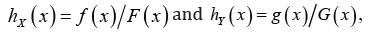,respectively.

Definition 2.1. A random variable X is said to be smaller than Y in the:

I. Likelihood ratio order (denoted as 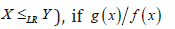is increasing in x≥0.

II. Usual stochastic order (denoted as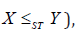if 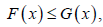for all 0.x

Definition 2.2. The nonnegative random variable X is said to have:

i. Increasing (decreasing) likelihood ratio property [ILR (DLR)], if f is a log-concave (log- convex) function on ()

ii. Increasing [Decreasing] Failure rate (IFR [DFR]) property, if h_x(x)is increasing [decreasing] in x≥0, or equivalently if, F(x))is log-concave [log-convex] for x≥0.

Karlin [8] introduced the concept of Sign-Regular of order 2, which is of great importance in various fields of Mathematics and Statistics with many applications.

Definition 2.3. A nonnegative function β(x,y) is said to be totally positive (reverse regular) of order 2, denoted as TP₂(RR₂)in 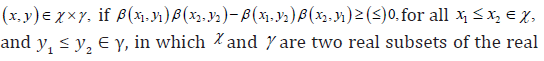line R.

Main Results

As Nair, et al. [4] pointed out, comparison of the different ageing properties of X and X* will often help in the selection of appropriate model and its analysis in a practical situation. In this section, we discuss preservation properties of some aging notions under the transformation *XX→in the EAHM introduced in this paper. Before stating the results, we must state the following useful lemma.

Lemma: Let V≥0 be a random variable with distribution function from the family 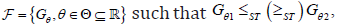for all 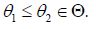Suppose a measurable real function ϕ(θ,v) for which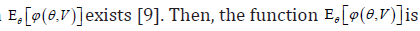

a) Decreasing in ,θ if ϕ(θ,v) is decreasing (increasing) in v and decreasing in θ.

b) Increasing in ,θ if ϕ(θ,v) is increasing (decreasing) in v and increasing in θ.

It is well-known in the literature (see, for example, Shaked, et al. [5]) that the log-convexity property of the density function implies the log-convexity property of the survival function. In other words, the DLR property is stronger than the DFR property. Therefore, it is useful to study conditions under which the DFR property of the baseline variable is translated to the DLR property of the overall variable in the EAHM.

heorem: Let X be DFR, let a(x,y) be decreasing in ,x for all z≥0, and decreasing (increasing) in z,for any x≥0, and let such that it is log-convex in x, for any z≥0. Then X* is DLR.

Proof: In view of Raeisi, et al. [1], the density function of X* is given by

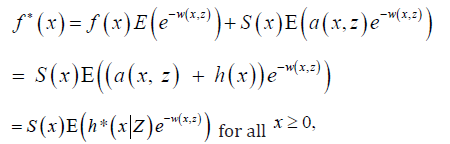
Where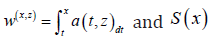 is survival function of .X To get the proof it suffices to prove that 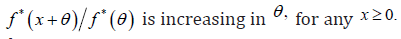First, we can see that

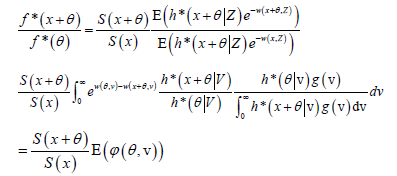
Where 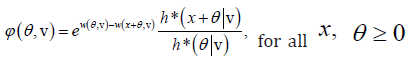and V is a nonnegative random variable with density function g_θ for any θ≥0, given by

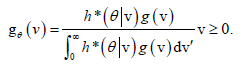
When X is DFR, the ratio 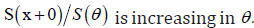Thus, it is enough to show by Lemma 4.1 that E(ϕ(θ,v)) is increasing in θ. Let us observe first that

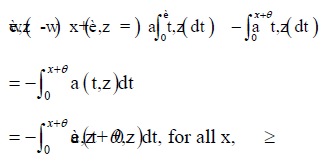
Because, by assumption, (),axzis decreasing in ,x for all 0,z≥ it is therefore clear from above that 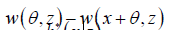is increasing in θ, for all 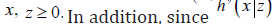is, from assumption, log-convex in ,x for any 0,z≥thus

is increasing in ,θ for each 0.z≥ It now follows that (),vϕθ is increasing in ,θ for all 0.v≥ On the other hand, we can observe that if (),axz is decreasing (increasing) in ,z for all x≥0 and 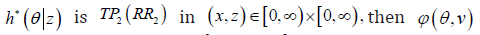is increasing (decreasing) in

Denote by G_θ the distribution function of ,V for any 0.θ≥ Then, it is easy to see that 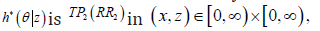if and only if that 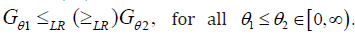Because the LR order implies the ST order (cf. Shaked, et al. [5]), it consequently follows that that 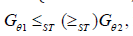for all 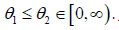An application of Lemma 4.1(ii) completes the proof. For some similar investigation in context of other reliability models we invite the readers to see Theorem 3.6 in Xu, et al. [10].

Conclusion

In this paper, we obtained further properties of some aging notions under the transformation *XX→in the EAHM [11,12]. Similar results can be obtained in the case of the ageing concepts, DMRLHA, NBUC, UBA and UBAE (see Lai & Xie [6] and Barlow & Proschan [7] for definition of these concepts) using the same kind of arguments. EAHM can be used in medical and epidemiological studies. We consider a patient with a prostate cancer disease. The time is an important factor for covariate variables (sex, age, effect of drugs,…) because it can be possible that a new and better drug is found. Hence, hazard rate can be changed.

References

1. Raeisi M, Yari Gh (2016) Some Dependencies, Stochastic Orders and Aging Properties in an Extended Additive Hazards Model. Iranian Journal of Science and Technology. Transactions A: Science DOI: 10.1007/s40995-016-0119-3.
2. Aalen OO (1980) A model for nonparametric regression analysis of counting processes. Lecture Notes in Statistics 2: 1-25.
3. Aalen OO (1989) A linear regression model for the analysis of life times. Stat Med 8(8): 907-925.
4. Nair NU, Sankaran PG (2012) Some results on an additive hazards model. Metrika 75: 389-402.
5. Shaked M, Shanthikumar JG (2007) Stochastic orders. Springer, New York.
6. Lai CD, Xie M (2006) Stochastic ageing and dependence for reliability. Springer, New York.
7. Barlow RE, Proschan F (1981) Statistical Theory of Reliability and Life Testing. Silver Spring, Maryland.
8. Karlin S (1968) Total Positivity. Stanford University Press.
9. Misra N, Van Der Meulen EC (2003) On stochastic properties of m-spacings. Journal of Statistical Planning and Inference 115: 683-697.
10. Xu M, Li X (2008) Negative dependence in frailty models. Journal of Statistical Planning and Inference 138: 1433-1441.
11. Li P, Ling X (2012) The additive hazard mixing models. Acta Mathematicae Applicatae Sinica. English Series 28(1): 139-148.
12. Nelsen RB (2006) An Introduction to Copulas. Springer, New York