Review Article

Further Developments on the T-Transmuted X Family of Distributions

Clement Boateng Ampadu¹* and Girish Babu²

¹31 Carrolton Road, Boston, MA 02132-6303, USA

²Department of Statistics, Government Arts and Science College, India

Submission: April 12, 2018; Published: July 09, 2018

*Corresponding author: Clement Boateng Ampadu, 31 Carrolton Road, Boston, MA 02132-6303, USA; Email: drampadu@hotmail.com

How to cite this article: Clement B A, Girish B. Further Developments on the T-Transmuted X Family of Distributions. Biostat Biometrics Open Acc J. 2018; 7(4): 555720. DOI: 10.19080/BBOAJ.2018.07.555720

Abstract

We review the T-Transmuted Family of Distributions introduced in [1] and propose some further developments of this class of distributions.

Keywords: T-X(W) family of distributions; Transmuted family of distributions; Biological data; Health data; Quadratic rank; Transmutation map; Monotonic; Beta-generated; Random variable; Integral representation; Base distribution; Plethora; Probability distributions; Quantile function

Introduction

Transmuted family of distributions

According to the quadratic rank transmutation map (QRTM) approach in [2], the CDF of the transmuted family of distributions is given by

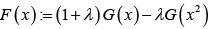
Where −1≤λ≤1 and G(x)c is the CDF of the base distribution. When 0λ= we get the

CDF of the base distribution

Remark 1.1. The PDF of the transmuted family of distributions is obtained by differentiating the CDF above.

A plethora of results discussing properties and applications of this class of distributions have appeared in the literature, and for examples see [3]

T-X(W) family of distributions

This family of distributions is a generalization of the beta-generated family of distributions first proposed by Eugene et.al [4]. In particular, let r(t) be the PDF of the random variable T∈[a,b] ,−∞≤a< b ≤∞ and let ()()WFx be a monotonic and absolutely continuous function of the CDF F(x) of any random variable .X The CDF of a new family of distributions defined by Alzaatreh et.al [5] is given by

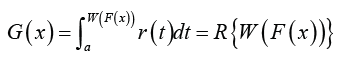
Where R(⋅) is the CDF of the random variable T and a≥0

Remark 1.2. The PDF of the T-X(W) family of distributions is obtained by differentiating the CDF above

Remark 1.3. When we set 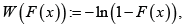then we use the term “T-X Family of Distributions” to describe all sub-classes of the T-X(W) family of distributions induced by the weight function W(x)=−ln(1-x) A description of different weight functions that are appropriate given the support of the random variable T is discussed in [5]. A plethora of results studying properties and application of the T-X(W)family of distributions have appeared in the literature, and the research papers, assuming open access, can be easily obtained on the web via common search engines, like Google, etc.

T-Transmuted X family of distributions

This class of distributions appeared in [1]. In particular the CDF admits the following integral representation for a≥0

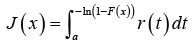
Where r(t) is the PDF of the random variable T and F(x) is the transmuted CDF of the random variable ,X that is,

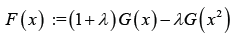
Where −1≤λ≤1 and G(x)c is the CDF of the base distribution.

Remark 1.4. The PDF of the T-Transmuted Xfamily of distributions is obtained by differentiating the CDF above.

Further developments

In this section, inspired by quantile generated probability distributions [6], we propose some new extensions of the T-Transmuted X family of distributions. We give the CDF of these new class of distributions, only in integral form. However, the CDF and PDF can be obtained explicitly by applying Theorem 2.2 and Theorem 2.3, respectively [7].

The q_T X− family of distributions

Definition 2.1. Let V be any function such that the following holds:

I.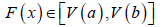

II. F(x) is differentiable and strictly increasing

III. 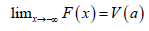and 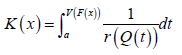then the CDF of the q_T X− family induced by V is given by

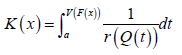
Where 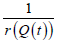is the quantile density function of random variable [],,Tab∈ for ,ab−∞≤<≤∞ and F(x) is the CDF of any random variable X.

Theorem 2.2. The CDF of the q_T X−c family induced by V is given by

K(x)=Q[V(k(x))]

Proof. Follows from the previous definition and noting that

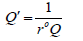
Theorem 2.3. The PDF of the q_T X− family induced by V is given by

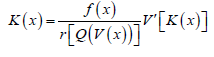
Proof. ,k=K′,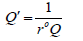F′=f, and K is given by Theorem 2.2

Remark 2.4. When the support of T is [a,∞) where a≥0, we can take V as follows

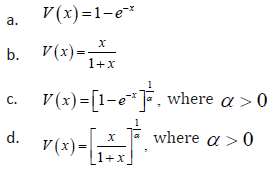
Remark 2.5. When the support of T is (−∞,∞) we can take V as follows

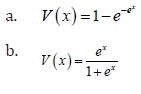
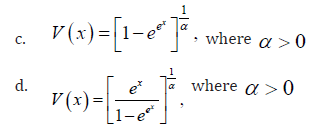
Some q_T transmuted X family of distributions

In what follows we assume the random variable T has PDF r(t) and quantile function Q(t) We also assume the random variable X has transmuted CDF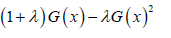

Where −1≤λ≤1 and G(x) is the CDF of the base distribution.

Families of q_T transmuted X distributions of Type I

The CDF has the following integral representation for α>0 and α≥0

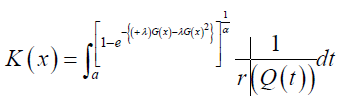
Families of q_T transmuted X distributions of Type II

The CDF has the following integral representation for 0α> and 0α≥

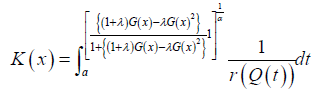
Families of q_T transmuted X distributions of Type III

The CDF has the following integral representation for α>0

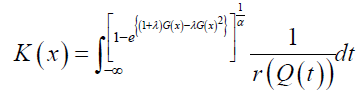
Concluding Remarks

Our hope is that researchers will find these class of distributions practically significant in modeling biological data, health data, etc. We hope the researchers will further develop the properties and applications of these new class of distributions.

References

1. Jayakumar K, Girish Babu M (2017) T-Transmuted X Family of Distributions. Statistica 77: 3
2. Shaw W, Buckley I (2007) The alchemy of probability distributions: beyond Gram-Charlier expansions, and a skew-kurtotic-normal distribution from a rank transmutation map. Research report.
3. Faton Merovci, Ibrahim Elbatal (2014) Transmuted Weibull-geometric distribution and its applications, Scientia Magna 10(1): 68-82
4. Eugene N, Lee C, Famoye F (2002) The beta-normal distribution and its applications. Communications in Statistics-Theory and Methods 31(4): 497-512.
5. Alzaatreh A, Lee C, Famoye F (2013) A new method for generating families of continuous distributions. Metron 71(1): 63-79.
6. Clement Boateng Ampadu (2018) Quantile-generated family of distributions: a new method for generating continuous distributions. Fundamental Journal of Mathematics and Mathematical Sciences 9(1): 13-34.
7. Muhammad S, Robert K, Irene Le (2016) Transmuted Gompertz Distribution: Properties and Estimation. Pak J Statist 32(3): 161-182.