Will P‐Value Triumph over Abuses and Attacks?
Jyotirmoy Sarkar*
Department of Mathematical Sciences, Indiana University‐Purdue University Indianapolis, USA
Submission: March 29, 2018; Published: July 09, 2018
*Corresponding author: Jyotirmoy Sarkar, Department of Mathematical Sciences, Indiana University‐Purdue University Indianapolis, Indianapolis, IN 46202; USA, Tel: 317‐274‐8112; Fax: 317‐274‐3460; Email: jsarkar@iupui.edu
How to cite this article: Jyotirmoy S. Will P-Value Triumph over Abuses and Attacks?. Biostat Biometrics Open Acc J. 2018; 7(4): 555718. DOI: 10.19080/BBOAJ.2018.07.555718
Abstract
The null hypothesis significance testing procedure (NHSTP) was devised to guide scientific researchers decide whether an observed difference between comparative groups is due to chance or if there is a significant effect. However, prolific use of NHSTP by non‐statisticians in many quantitative studies has resulted in widespread misinterpretations, misuses and abuses. We briefly recall a recent ban on p-value and summarize the official statement written by the American Statistical Association (ASA), which explains what p‐value is, what it is not, and how to interpret and use it correctly
Keywords: Test statistic; Type I error; Type II error; Sampling distribution; Point estimate; Standard error; Power; Statistical significance; Multiple testing; Practical significance; Null hypothesis; Chi‐squared test; Alternative hypothesis; P‐value; Probability; Unbiased estimator; Sampling distribution; Random sample; Null distribution; Bayesian point; Willy‐nilly
Abbrevations:NHSTP: Null Hypothesis Significance Testing Procedure; ASA: American Statistical Association; DF: Degrees of Freedom; FDA: Food & Drug Administration; CIs: Confidence Intervals
Introduction
In this review, we present in a non‐statistician’s language the fundamental statistical inferential methodology known as the null hypothesis significance testing procedure (NHSTP). It purports to answer the question: “When we observe some differences between comparative groups, could they have arisen by chance even though there is no real effect, or is there a significant effect?” To guide scientific researchers answer this question, statisticians have devised with extreme care the NHSTP. Specifically, they quantify the weight of evidence in the entire data against the null hypothesis of no effect in one number- p-value; but they do so only after they have followed a long list of safeguards to ensure the proper use of NHSTP.
In Section 2, we describe the genesis of p‐value, its definition, correct interpretation and proper use. In Section 3, we address some widespread misinterpretations of p-valuearising usually out of incomplete knowledge, but sometimes out of deeply held beliefs to the contrary; and we equip the reader to counter such misinterpretations. Next, in Section 4, we mention the pitfalls of misuses and abuses of p-value. In Section 5, we recall a recent drastic action by one journal to ban the use of p-valuein their publications; and we summarize the reactions of academics to the ban. Section 6 presents a summary of the policy statement written by the American Statistical Association (ASA)-a statement that
a. Expounds the principles that declare what p‐value is and is not,
b. Lists approaches that can serve as alternatives to NHSTP and p‐value, and
c. Highlights some features of good statistical (and scientific) practice.
In Section 7, we conclude the paper by answering the question in the title of this paper, and outline what every practicing statistician must do to secure the rightful place of NHSTP and p‐value. Specifically, we should not only report a significant p-value, but also report all related issues such as which model is adopted, what assumptions are made, whether the data support these assumptions, how data are collected, and the list of all hypotheses tested and p‐values computed, including those that are not significant. We must supplement p-valuewith descriptive and graphical summaries of data, interval estimates of parameters; and we must disclose the achieved power of the NHSTP after adjusting for multiple testing, if any.
The proper place of pvalue
In this section, we answer the following questions: Why was the NHSTP developed? What exactly is p-value? How do we use p‐value? How do we interpret p‐value?
Genesis of pvalue
The first known use of p-valuewas in 1770 by Pierre‐Simon Laplace, who studied over half a million births, and concluded that there is an unexplained effect leading to an excess of boys compared to girls [1]. The concept of p‐value was formally introduced as a methodology by Karl Pearson [2] in the context of Pearson’s chi‐squared test designed to decide whether the observed difference between sets of categorical data can be attributed to chance alone. The method became known as NHSTP. Thereafter, Ronald Fisher popularized the NHSTP in a wide range of contexts in the 1920’s and 1930’s in his books [3,4]. Ever since its inception, statisticians have debated about its proper use and interpretation. See the list of references in [5].
Definition of p-value
p-value(also known as the observed significance) is the probability under a specified model that, when the null hypothesis () H0 holds, one would obtain a data (or, after summarization, a test statistic value) that is equal to or more extreme (in the direction of the alternative hypothesis) than the already observed value. In short, we may write
p-value=Pr(test statistic would be equal to or more extreme than observed | H0 is true )
Note that the alternative hypothesis plays an important role in the computation of p‐value by dictating the direction of “more extreme” values of the test statistic. According as the alternative hypothesis is left‐sided, right‐sided or two‐sided, the p-valueis the probability, under the sampling distribution of the test statistic when H0 holds, of the left tail, right tail or two tails combined.
Use of p-valueand choice of α
p-valueanswers the question: “Based on repeated independent samples of the same size, what proportion of time are we going to see a test statistic equal to or more extreme than the one we have already observed in the current sample, if indeed H0 holds true?” If this probability ()p-value is small, our sample must be extreme or incompatible with respect to H0 ; and if this probability is large, our sample is compatible with H0 . Therefore, we use the universal decision rule:
"Reject H0 if p-value<=α ,and do not reject H0 if if p-value>α
For example, a p-valueof .02 signifies that if H0 is true and if all other assumptions for NHSTP are valid, then there is a 2% chance of obtaining a result at least as extreme as the one observed. This p‐value being smaller than the standard choice of .05α= (we say more about this choice is the next paragraph), the scientist rejects 0.HLikewise, a p‐value of .32 signifies that if H0 is true and if all assumptions are valid, then there is a 32% chance of obtaining a result at least as extreme as the one observed. This p-valueis not so small, indicating that the data is compatible with H0 , and the scientist must not reject 0.
But how does one choose the threshold α Indeed, αdenotes the probability of type I error (false rejection of a true H0 ); it is called the (nominal) level of significance of the test; and it is a risk we are willing to take while applying the NHSTP. Furthermore, the test statistic itself is so chosen that it minimizes the probability of type II error (failure to reject a wrong H0 when a particular alternative hypothesis holds), denoted byβ. Equivalently, a preferred test is the one that maximizes the power1,β− which is the probability of rejecting H0 when a particular alternative hypothesis holds. By choosing the sample size sufficiently large, one can ensure that the probability of type II error, when the effect size is a specified practically important amount, is also reasonably low (or, the power is sufficiently high). However, as the adage says, “There aren’t no such thing as a free lunch.” For any fixed sample size, as one sets αlower, one simultaneously makes βlarger! Therefore, the threshold α ought to depend on the relative costs of making the two types of error. (For example, in medicine the rationale is that it is better to tell a healthy patient “we may have found something-let’s test further,” than to tell a diseased patient “all is well.” On the contrary, in criminology it is preferable to release a guilty person than to convict an innocent person.) Nevertheless, in practice, in an overwhelming number of cases, regardless of the sample size, αis taken to be .05. There is nothing sacrosanct about .05; but it continues to prevail, perhaps because Fisher proposed 1 in 20 as a reasonable threshold, even though he further commented that the threshold could as well be 1 in 50, or 1 in 100.
Interpretation of pvalue
Other than falling on one side of the threshold α or the other-leading to a decision to reject H0 or not-the actual p‐value also quantifies the weight of evidence against either the H0 or the underlying assumptions-the smaller the p-value, the stronger the evidence. However, a low p-valueis just one piece of the evidence against H0 . The totality of evidence must include a discloser of the model adopted, assumptions made and verified, method of data collection, descriptive and graphical summaries of data, interval estimates of parameters, all hypotheses tested and p-value computed, including non‐significant p-value. The next section dispels some common misinterpretations of p-value.
Misinterpretations of p‐value and how to dispel them
Over the years, p-valuehas become like a litmus test for establishing statistical significance (or departure from H0 ) in almost all quantitative disciplines such as biology, chemistry, clinical trials, criminology,economics, education, engineering, finance, marketing research, medicine, physics, political science,psychology, and social science. Unfortunately, in the hands of otherwise well‐meaning scientists who arestatistically untrained, p‐value has been often misinterpreted and misused. Many resources, includinginternet sites and even some textbooks, give wrong interpretations of p‐value causing unsuspecting readers to fall prey to misusing p-value-so much so that it has been a matter of considerable controversy. In 2014, statistician and science writer Regina Nuzzo [6]: “The p-valuewas never meant to be used the way it’s used today.
We won’t make an exhaustive list of possible misinterpretations and misuses of p-value. Instead, we mention only the two most common misinterpretations. The second most common misinterpretation is that p-valueis the probability that one will mistakenly reject a true H0. With this misinterpretation, when p-valueis small the misuser is lulled to believe that, the chance of making an error being small, it is highly likely he is not making an error by rejecting H0 . A p-valueof .005, for example, is misinterpreted to mean that there is only a 1/2% chance of making an error if he rejects H0 . Consequently, he comfortably rejects H0 , thinking that there is nothing else to worry about. Similarly, a p-value of .32 is misinterpreted to mean that there is a 32% chance (a high risk) of making an error if he rejects H0 ; therefore, he is better off not rejecting H0 . To guard against this misinterpretation one must realize that the probability of mistakenly rejecting a true H0 is actually .
Sellkeet al. [7] have estimated the actual error rates associated with different p-value, under some assumptions; thereby they have created a tool that makes p-valuemore easily interpreted. The most common misinterpretation of p-valueemerges from some people mistakenly thinking that it is theconditional probability that the null hypothesis is true, given the data (or given the test statistic); that is, they think p-value is Pr(H0 is true|data)is truedata,H But this is wrong! The widespread misuse of statistical significance (that is, “0.05”pvalue<=?) to claim a scientific finding (or an implied truth) causes considerable distortion of thescientific process. A p-valueof .002, for example, does not mean that there is only a .2% chance that H0 is true, nor does it mean that one has proved H0 is false. Similarly, a p-valueof .73 does not mean that there is a 73%chance that H0 is true. Dispelling this most common misinterpretation will require a lot more work for us. Wewill explain in the next four paragraphs below why such an interpretation is wrong.
What is the root cause of this most common misinterpretation of p-value? There is no single answer to thisquestion. But based on experience, we think it is because of a lack of understanding of the sampling distribution of the test statistic. Let us, therefore, elaborate on the concept of sampling distribution, and then relate p-valueto the sampling distribution of the test statistic when H0 holds (the so‐called null distribution).Imagine that different teams of scientists will go out, collect data independently, and compute the teststatistics. When they are done, their computed values of the test statistic will differ. Such a variation is aninherent nature of any random variable (and the test statistic is a random variable). A display of all suchvalues of the test statistic obtained by different teams of scientists gives the sampling distribution of the teststatistic. For example, the one‐sample t-statistic is a standardized version of the sample mean X, which is a point estimator of the parameter of interest-the population mean .μThe center of the sampling distributionof the sample mean equals the population mean, and hence we say that Xis an unbiased estimator of.μAn estimate of the standard deviation of the sampling distribution of Xis called its standard error, and it is given by S/n, where Sis the sample standard deviation and nis the sample size. The t-statistic
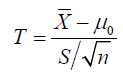
measures by how many standard errors the point estimatorXdiffers from the population mean0μspecified by the null hypothesis0.H when H0 holds, the sampling distribution of thestatistic,t−based on a random sample from a normally distributed population, is the so‐called t‐distribution with()1n−degrees of freedom(DF). Its density function, like that of the standard normal density, is symmetric and unimodal around zero;but its peak is less tall and its tails are thicker than the corresponding parts of the standard normal densitywhen the DF is small. Moreover, the t‐density approaches the normal density as the DF increases. Therefore, when H0 holds true, most scientists would obtain a t-statistic (in absolute value) closer to zero; but somewould obtain values in the tails because of randomness in the data! Similar explanation exists for the nulldistribution of any test statistic.In practice, a scientist obtains only one sample and hence only one value of the test statistic. How can thescientist determine whether the observed value of the test statistic is near the center of the null distribution,or in its tails? We need a measure of incompatibility with H0 and compatibility with the alternative hypothesis; and p-valueis that measure. P-valueis the proportion of scientific teams who would get, if H0 were true, a test statistic value equal to or more extreme (or more towards the alternative hypothesis) thanthe value this particular scientist obtained. Thus,p-valuequantifies the evidence in the data (or in the test statistic) against H0 and in favor of the alternative hypothesis—the smaller the p‐value, the stronger theevidence; and as such, it guides the scientist make a judicious choice: Reject H0 if ;p-value<=α and do not reject H0 if .p-value>α
Having made that choice-to reject H0 or not to reject H0 -the scientist is either right or wrong; but there isno way for anyone to determine whether the scientist’s decision is right or wrong, or even to assign aprobability that the decision is right! In other words, no one can computePr(H0 is true|data)is truedata,Hat least not in the framework of NHSTP, since there is nothing random about H0 being true or false; the randomness is onlyin the sampling of the data.On the other hand, if one takes a Bayesian point of view, one begins with a prior knowledge of Pr(H0 is true|data)is true;Hand then one updates that knowledge to a posterior after collecting data (or after computing the teststatistic). Berger & Delampady [8] exhibit dramatic conflicts between the Bayesian posterior probabilityPr(H0 is true|data)is truedata,Hand the frequentist.p-valuesome people mistakenly presume the twoconcepts are the same!
Pitfalls of misusing and abusing p-value
Here are some pitfalls of a foolhardy application of NHSTP without exercising proper checks and balances. Having found a statistically significant effect p-value<=.05 some scientists rush to publish their findings,often neglecting to check the power of the NHSTP and to verify whether the underlying assumptions arejustified. This is a misuse of the NHSTP. On the other hand, when they find no significance p-value<=.05,they assume reporting such findings will be in vain. In fact, many journals suffer from publication bias forthey publish only statistically significant results; and they decline to publish non‐significant results or resultsthat reproduce a previous finding, arguing that the latter two are not novel in appeal. Regrettably, publishedsignificance turns out to be spurious all too often; and other scientific teams cannot reproduce it.
Some researchers conclude that they have “discovered” significance simply because they have satisfied the bar "p-value<=.05."However, they may have done so by cherry picking promising findings, a practice alsoknown as data dredging, significance chasing and p‐hacking. This is an abuse of the NHSTP. Willy‐nillyapplication of multiple testing based on the same data (for example, doing post hoc pairwise comparisonsafter an analysis of variance) without adjusting the test‐wise probability of type I error inflates the overallprobability of type I error. In such multiple testing scenarios, individual p‐values are misleading, unless the test‐wise αis adjusted downwards to catch the highly statistically significant results. In addition, a givenstudy maybe sufficiently powered to detect a certain effect size when only one test is to be made; but it maylack sufficient power to detect the same effect size if several tests are to be performed.To prevent abuse of NHSTP, post hoc discovery of an effect, which was not initially planned for, is not anacceptable method of establishing a scientific truth; at best, it can serve as a basis for designing a follow‐upresearch study. This is why a pharmaceutical company must provide to the U. S. Food & Drug Administration (FDA) a detailed protocol before a clinical trial is carried out. If the data fail to reject the null hypothesisproposed in the protocol, but they point to some other new finding, the FDA will not accept such a finding.The company must conduct another clinical trial to establish their claim.
Furthermore, a small p-value, by itself, does not indicate the importance of a finding. We give three examples:A drug can have a statistically significant effect on patients’ blood cholesterol levels without having anytherapeutic effect. A vitamin may have a statistically significant increase on average life expectancy; but theestimated one‐day extension of life expectancy is hardly of any practical significance. In a designedexperiment involving many factors, some higher order interactions may turn out to be statistically significant;but a simpler model, which assumes such higher order interactions are mere noises, may fit the data quiteadequately.In 2005, John Ioannidis [9]: “It is misleading to emphasize the statistically significant findings of anysingle team. What matters is the totality of the evidence.” What also matters is the totality of the choices madeby the scientist-the number of hypotheses explored during the study, all data collection decisions, allstatistical analyses conducted, and allp-valuecomputed.
A ban on p‐value and reactions to the ban
In March 2015, editors David Trafimow and Michael Marks of Basic and Applied Social Psychology took an unprecedented, drastic decision to ban the use of p‐value, as well as confidence intervals (CIs), in theirjournal [10]. Instead, BASP requires strong descriptive statistics, including effect sizes, and encourage thepresentation of frequency or distributional data when feasible, and also encourage the use of larger samplesizes (although they stop short of requiring particular sample sizes). They argue, “The NHSTP has dominatedpsychology for decades; we hope that by instituting the first NHSTP ban, we demonstrate that psychologydoes not need the crutch of the NHSTP, and that other journals follow suit.” Although, the controversy has been looming since 1960 [11], the BASP ban on p-valueshocked statisticians and created quite a fuss among researchers. The Royal Statistical Society solicited letters fromacademics to express how they felt about the ban. These letters all tell a similar story- p-valueare prone to misuse and misinterpretation; and we need to be more careful about how we design and interpret the resultsof our experiment; but we must not throw out the entire NHSTP.
Within two months of the BASP ban onthree British psychologists wrote [12]: “CIs offer an asyet undeveloped but potentially very valuable tool for psychologists to interpret their data.” They point outthat the reason for the original development of NHSTP (along with CIs of effect sizes) was to guideresearchers how they should act in the future based on whether they found a real effect or not. Whatguidelines should researchers follow to make such fundamental decisions if CIs and NHSTP are banned?Furthermore, while supporting BASP’s recommendation for large sample sizes to increase the precision of theestimates, they argue that reporting that precision through CIs should be required, rather than forbidden.The ban was so radical that for the first time in its 175 years of existence, the American Statistical Association(ASA) Board took position on a specific matter of statistical practice, and developed a policy statement on p-valueand statistical significance. A team of over two dozen prominent statisticians took nearly a year tocreate this policy statement. With this statement, the ASA hopes to shed light on an aspect of Statistics that istoo often misunderstood and misused in the broader research community, and to open a fresh discussion anddraw renewed and vigorous attention to changing the practice of science with regards to the use of statisticalinference. The full ASA statement is found in [5]. Below we give only a brief summary.
Summary of the ASA Statement
The ASA statement begins with the definition of p-valueas we already gave in Subsection 2.2 above.Then it proposes six principles that can improve the conduct or interpretation of quantitative science; next, itmentions some other approaches as alternatives to p-valueand NHSTP; and finally, it concludes with a list oftraits of a good statistical practice. For the readers’ benefit, we summarize them below.
Principles
I. P‐values can indicate how incompatible the data are with a specified statistical model. The smaller
II. the p-value, the greater the statistical incompatibility of the data with the null hypothesis, if the
III. underlying assumptions used to calculate p-valuehold.
IV. P‐values do not measure the probability that the studied hypothesis is true, or the probability that
V. the data were produced by random chance alone.
VI. Scientific conclusions and policy decisions should not be based only on whether a p-valuepasses a
VII. specific threshold. Even though pragmatic considerations often require “yes‐no” decisions, this does
VIII. not mean that p-valuealone can ensure that a decision is correct or incorrect.
IX. 4.Proper inference requires full reporting and transparency. Whenever a researcher chooses what to present based on statistical results, valid interpretation of those results is severely compromised if the reader is not informed of the choice and its basis.
X. A p-valuedoes not measure the size of an effect or the importance of a result. Any effect, however tiny, can produce a small p-valueif the sample size or measurement precision is high enough, and large effects may produce big p-valueif the sample size is small or measurements are imprecise.Also, identical estimated effects will have different p‐values if the precision of the estimates differs.
XI. By itself, a p-valuedoes not provide a good measure of evidence regarding a model or hypothesis. A p-valuewithout context or other evidence provides limited information. Data analysis should not end with the calculation of a p-valuewhen other approaches are appropriate and feasible.
Other approaches
Approaches other than p‐value and NHSTP include methods that emphasize estimation over testing, such asconfidence, credibility, or prediction intervals; Bayesian methods; alternative measures of evidence such aslikelihood ratios or Bayes factors; and decision‐theoretic modeling and false discovery rates. All thesemeasures and approaches rely on further assumptions; but they may more directly address the size of aneffect (and its associated uncertainty), or declare that the hypothesis is tenable.
Features of good statistical practice
Good statistical practice, as an essential component of good scientific practice, emphasizes principles of goodstudy design and conduct, a variety of numerical and graphical summaries of data, understanding of thephenomenon under study, interpretation of results in context, complete reporting and proper logical andquantitative understanding of what data summaries mean. No single index should substitute for scientificreasoning.
Summary and Conclusion
The concept of NHSTP and p-valuewas designed to answer the question: “When we observe some differencesin the comparative groups, could they have arisen by chance even though there is no real effect, or is there asignificant effect?” It was meant to guide the researcher how to proceed in future: To continue to subscribe tothe null hypothesis of no effect, or to switch allegiance and subscribe to the alternative hypothesis ofsignificant effect. Whatever the recommended decision, the scientist must acknowledge the potential forcommitting one type of error or the other, even though they held the probabilities of committing such errorsbelow reasonable bounds. The NHSTP was not meant to establish the truth one way or another, nor is itsupposed to substitute for the scientific task of explaining why the effect is there or not there. Therefore, p-valuedeserves neither super‐glorification nor outright denouncement.
We are optimistic that the answer to the question in the title of this paper is affirmative. When proper safeguards are taken to apply the NHSTP correctly, p-valueperforms its designated task just fine. Therefore,banning its use by one journal will not cause its demise. However, to let p-value secure its rightful place, firstwe must carefully ensure the following:
a. The sample size is large enough;
b. The sample is random; and
c. There is no bias.
Then we must disclose all choices made during formulation of hypotheses based on experts’scientific judgment about their plausibility and results of similar studies. Next, we must choose appropriateexperimental design to collect relevant data. Finally, we must report a comprehensive set of inferentialstatistics, including supporting evidence for all assumptions. In case of multiple testing, we must adjust thetest‐wise error rates to control the overall probability of type I error and to correctly identify which p-valueis statistically significant. When the statistician’s work is over, we must let the scientific experts wrestle withthe scientific justifications of the statistical findings. Onward with the responsible use of NHSTP!
Acknowledgement
I sincerely thank my colleagues and students who reviewed an earlier draft, offered many valuablesuggestions and generously contributed some illustrative examples leading to an improved version.
References
- Stigler Stephen M (1986) The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press, USA.
- Pearson Karl (1900) On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophical Magazine, 50(302): 157-175.
- Fisher Ronald (1925) Statistical Methods for Research Workers. Edinburgh: Oliver & Boyd, UK.
- Fisher Ronald (1971) The Design of Experiments (9th edn). Macmillan.
- Wasserstein R L, Lazar NA (2016) The ASA’s statement on p‐values: context, process, and purpose. The American Statistician 70(2): 129- 133.
- Nuzzo R (2014) Scientific method: Statistical errors. Nature 506(7478): 150-152.
- Sellke T, Bayarri MJ, Berger J (2001) Calibration of p values for testing precise null hypotheses. The American Statistician 55(1): 62-71.
- Berger JO, Delampady M (1987) Testing precise hypotheses. Statistical Science 2: 317-335.
- Ioannidis JPA (2005) Why most published research findings are false. PLoS Med 2(8): e124.
- Trafimow D, Marks M (2015) Editorial. Basic and Applied Social Psychology 37(1): 1-2.
- Krantz David (1999) The null hypothesis testing controversy in psychology. Journal of the American Statistical Association 94(448): 1372-1391.
- Morris Peter, Fritz C, Smith G (2015) Letter to the Editor: In defense of inferential statistics. The Psychologist 28(5): 338-339.






























