Mini Review

A Note on Optimal Partial Triallel Cross Designs

Anshula Pandey¹, Addisu Jember² and MK Sharma¹*

¹Department of Statistics, Sunandan Divatia School of Science NMIMS, India

²Addis Ababa University, Addis Ababa, Ethiopia

Submission: March 26, 2018; Published: July 09, 2018

*Corresponding author: Anshula Pandey, Department of Statistics, Sunandan Divatia School of Science NMIMS, Mumbai, India; Email: mk_subash@yahoo.co.in

How to cite this article: Anshula P, Addisu J, MK Sharma. A Note on Optimal Partial Triallel Cross Designs. Biostat Biometrics Open Acc J. 2018; 7(4): 555717. DOI: 10.19080/BBOAJ.2018.07.555717

Summary

Two simple alternative methods of construction of optimal partial triallel cross designs (unblocked and blocked) for p>3 lines are proposed by using transversal and parallel transversals of a Latin square of order p, where p is a prime or power of a prime. Sharma et al. [1] and Sharma & Fanta [2] also constructed these designs by using two mutually orthogonal Latin squares but we constructed these designs only taking one Latin square. Therefore our methods are simple in comparison to their methods. These designs are found to be optimal in the sense of Kiefer [3] and Das & Gupta [4].

Keywords: Partial triallel cross; Transversal; Parallel transversals; Mutually Othogonal; Latin Squares; Mating design; Cross designs; Mating designs; Randomized complete; Homogeneous blocks; Unblocked designs; Optimal block; Three-way hybrids; Half–parents; Triplet; Offspring; Directrix; cyclically mod; Parallel transversals

Abbrevations:CRD: Completely Randomized Design; RCB: Randomized Complete Block; PTC: Partial Triallel Crosses; BIB: Balanced Incomplete Block; GPBIBD: Generalized Partially Balanced Incomplete Block Designs

Introduction

Triallel crosses form an important class of mating designs, which are used for studying the genetic properties of a set of inbred lines in plant breeding experiments. For p inbred lines, the number of different crosses for a complete triallel experiment is 3^pC₃=p(p-1)(p-2)/2 of the type (iXj)k.i≠j≠k=0,1,2,…,p−1 Rawlings & Cockerham [5] were the first to introduce mating designs for triallel crosses. Triallel cross experiments are generally conducted using a completely randomized design (CRD) or a randomized complete block (RCB) design as environmental design involving 33 pCcrosses. Even with a moderate number of parents, say 10,p=in a triallel cross experiment; the number of crosses becomes unmanageable to be accommodated in homogeneous blocks. For such situations, Hinkelmann [6] developed partial triallel crosses (PTC) involving only a sample of all possible crosses by establishing a correspondence between PTC and generalized partially balanced incomplete block designs (GPBIBD). Ponnuswamy & Srinivasan [7] and Subbrayan [8] obtained PTC using a class of balanced incomplete block (BIB) designs. Dharmlingum [9] also constructed PTC using Trojan squares. Actually Trojan squares are MOLS. Other research workers who contributed in this area are Arora & Aggarwal [10,11], Ceranka et al. [12]. More details on triallel cross experiments can be found in Hinkelmann [13] and Narain [14].

Das & Gupta [4] constructed block designs for triallel crosses by using nested balanced block design with parameters v=p,b₁,b₂,k₁,k₂=3 Their method yields designs which are universally optimal in D (),,,pbkthe class of connected block designs for triallel crosses in p lines with b blocks each of size k such that the total number of experimental units are 33.pC< Sharma et al. [1] and Sharma and Fanta [2] also constructed optimal block and unblocked designs for PTC using two mutually orthogonal Latin squares together. We, in this paper, are proposing unblocked and blocked designs for triallel cross experiments by using transversal and parallel transversal of a Latin square. Our methods are different from Sharma et al. [1] and Sharma & Fanta [2] methods. These designs are found to be optimal in the sense of Kiefer [14] and Das & Gupta [4].

Definition

Definition 2.1: The triallel cross (T.C.) has been defined by Rawlings & Cockerham [5] as a set of all possible three-way hybrids among a group of (inbred) lines. Given three lines ,ij and ,kthere are distinct triallel crosses, namely (iXj)k,(jXk)i and (iXk)j involving these three lines. Thus given a set of plines, the TC will consist of a set of [p(p-1)(p-2)/2]distinct three way crosses. Each line will occur in r_H= (p-1)(p-2) three-way crosses as a half –parents and in r_F= (p-1)(p-2) three way crosses as a parent. Similarly, each pair of lines will occur in r_d=(p-2) three-way crosses both of them as half-parents and r_s=(p-2) three way crosses with one of them as half-parent and other as a parent.

Definition 2.2: Hinkelmann [6] proposed the definition of PTC as given below:

Suppose we have plines which are denoted by i=1,2,...,p A three way cross is then represented by a triplet (iXj)k where (iXj) stands for an offspring of the single cross .(iXj) We shall call i and j half-parents and kfull-parent. The crosses (iXj)k,(jXi)k,k(iXj) and k(JXi)are considered to be identical in three way crosses. Then PTC can be defined as follows:

A set of matings is said to be a PTC if it satisfies the following conditions:

Each line occurs exactly Hr times as half-parent and Frtimes as full parent.

Each cross (i×j)kccurs either once or not at all.

The total number of crosses is p r_F and r_H=2 .r_F Let ,r_Fhsub>=2.

Construction of partial triallel cross

Method 1: The first method of construction of PTC mating design is based on transversal (directrix) of Latin square of order ,p where pis a prime or power of prime. Start with a Latin square of order p and border the columns and the rows of square with elements of the transversal (directrix) (where transversal or directrix of a Latin square of order p in a set of p cells each row, column and symbol is represented exactly once in the set; see Hedayal & Seiden [15]. Each cell together with the border elements give a triplet of the type (i×j)×k where i≠j≠k=0,1,……,p−1 in the upper and lower triangular and triplet of the type (i×j)×k where i=j=k=0,1……p−1 in the diagonal of the mating design. Now deleting the triplet appearing in the diagonal of the mating design we get a mating design for PTC experiment which satisfy the condition of PTC. The method is illustrative below with example.

Example 1: Consider the following Latin square of order 5 transversal bracketed.

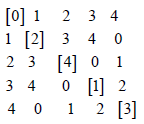
Now we border the columns and rows of the above Latin square by the bracketed elements of the transversal. We get the following arrangement.

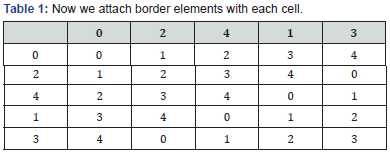
Now we attach border elements with each cell (Table 1). Then we get the following design

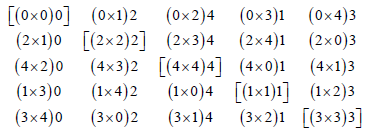
Now deleting the bracketed cells, we get following unblocked design d1 for PTC in which

i. Each line occurs r_H=(8) lines as half parent and r_F=(4) lines as full parent.

ii. Each triple cross (i×j)k either once or not at all in d₁.

iii. We denote the unblocked design as d₁εD(p,n)with plines and nexperimental units.

Design d₁

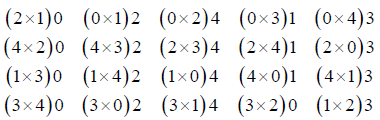
From the above mating design, we can derive block design for PTC. Consider the triplet of any column of the above mating designs as initial blocks and then developing row-wise cyclically mod (5) these blocks, we get block design for PTC. We denote this design d₂εD(p,n) with p=5,b=4 and k=5./p>

Consider the first column triplets as 4 initial blocks and then developing cyclically mod (5), we get the following block design for PTC, which satisfy the condition of PTC.

Design d₂

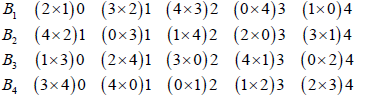
Example 2: Now consider the following Latin square of order 5 transversal bracketed.

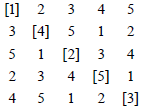
Following the procedure of example 1, we get following unblocked mating design d₃εD(p,n) for PTC with p=5 and n=20 experimental units.

Design d₃

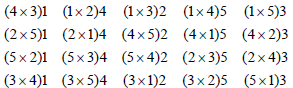
By observing the above design we find that every triple cross occurs two times in the design. Hence this design is different from the design given in example 1. Again by taking triplets of any column as initial blocks and developing each triplet cyclically row-wise mod (5) we obtain block design 4dwith parameters 5,p= 4b=and 5k=in which each triple cross is also replicated two times in the design.

Design d₄

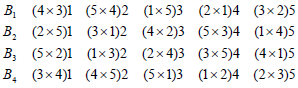
We see that unblocked design d₁ is different from unblocked design d₃ and blocked design d₂ is different from blocked design d₄ Thus we get two different (unblocked and blocked) designs by using transversal of two Latin squares of order 5 which are mutually orthogonal.

a) Remark 1: It is impossible to construct PTC from Latin square of order 6 because the Latin square of order 6 does not contain distinct elements in the transversal (directrix).

b) Remark 2: we know that when pis a prime or power of a prime then there exist p-1 or pⁿ-1 mutually orthogonal Latin squares. Out of p-1 or pⁿ-1 m.o.l.s., we can use only transversals of p-2or pⁿ-2 atin squares for the construction of mating designs for PTC because transversal of only one Latin square does not contain distinct elements.

c) Remark 3: Out of p-2or pⁿ-2 Latin squares only one Latin square will give mating design for PTC in which every triple cross occurs two times in unblocked and blocked designs.

Method 2: Two transversals in a Latin square of order pare called parallel if they have no element in common. Suppose we have identified such parallel transversals in a Latin square and border the columns and rows of a Latin square with the elements of parallel transversals for example if the parallel transversal element ijabelong to thi row and thjcolumn then this element will border the thi row and thjcolumn of the Latin square. Thus we get triallel cross mating design with the difference that triplet of the type (i×j)×k where i=j=k=0,1……p−1 occurs on the positions of parallel transversal elements and triplet of the type (i×j)×k where i≠j≠k=0,1,……,p−1 occurs below and upper positions of parallel transversals.

Now deleting the triplet appearing at the parallel transversal positions in the triallel cross mating design we get a mating design 5dfor PTC experiment which satisfy the condition of PTC. The method is illustrative below with example.

Example 3: Consider the following 5×5 Latin square with two parallel transversals with square bracketed:

Now we border the columns and rows of the above Latin square by the bracketed elements of the parallel transversals following the rule given in method 2. We get the following arrangement.

Now we attach border elements with each cell. Then we get the following triallel cross mating design

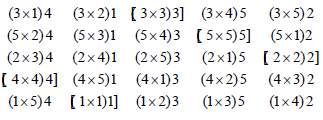
Now deleting the bracketed cells, we get following unblocked design d5 for PTC in which

Each line occurs (8)Hr= lines as half parent and r_F=(4) lines as full parent

Each triple cross (i×j)k either once or not at all in d⁵

Design d₅

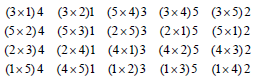
From the above mating design, we can derive blocked mating design for PTC. Consider any column of the above mating designs as initial blocks and then developing these blocks cyclically row wise mod(5), we get blocked mating design 6dfor PTC with parameters 5,p= 4b= and 5k

Design d₆

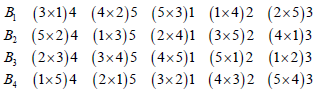
Sharma et al. [1] and Sharma & Fanta [2] constructed these designs by using two M.OL.S. of order p together, where p is a prime or prime power but our method needs only one Latin square.

d) Remark 4: When we take parallel transversals out of p-2 or pⁿsup>-2 Latin squares only one Latin squares will give mating design for PTC in which every triple cross occurs two times in unblocked and blocked designs.

References

1. Sharma MK, Asedewoin A, Misganaw B (2011) Optimal partial triallel cross designs. MASA 6: 1-8.
2. Sharma, M.K. and Fanta, S. (2012). Optimal partial triallel crosses. Jour Indian Society of Ag Statistics 66(2): 1-6.
3. Kiefer J (1975) Construction and optimality of generalized Youden designs, in a survey of Statistical Design and Linear Models. In: Srivastava JN (Eds.), Amesterdam: North Hollond, Netherlands, pp. 33-53.
4. Das A, Gupta S (1997) Optimal block designs for triallel cross experiments. Commu Stat-theory and Methods 26(7): 1767-1777.
5. Rawlings JO, Cockerham CC (1962) Triallel analysis. Crop Sci 2: 228-231.
6. Hinkelmann K (1965) Partial triallel crosses. Sankhya A 27: 173-196.
7. Ponnuswami, K.N. and Srinivasan,M.R. (1991). Construction of partial triallel crosses (PTC) using a class of balanced incomplete block designs (BIBD). Commu Stat-Theory and Methods A20: 3315-3323.
8. Subbarayan A (1992) On the applications of pure cyclic triple system for plant breeding experiments. Jour of Applied Stat 19(4): 489-500.
9. Dharmalingam M (2002) Construction of Partial Triallel Crosses based on Trojan square design. Jour of Applied Stat 29(5): 695-702.
10. Arora BS, Aggarwal KR (1984) Confounded triallel experiments and their applications. Sankhya B 46(1): 54-63.
11. Arora BS, Aggarwal KR (1989) Triallel experiments with reciprocal effects. Jour Ind Soc Agril Stat 41: 91-103.
12. Ceranka B, Chudzik H, Dobek A, Kielczewska H (1990) Estimation of parameters for triallel crosses compared in block designs. Statist Appl 2: 27-35
13. Hinkelmann K (1975) A Survey of Statistical Design and Linear Models. Amsterdam, North Hollond, Netherlands, Pp. 243-269.
14. Narain P (1990) Statistical Genetics. Wiley Eastern Limited, New Delhi, India.
15. Hedayat AS, Seiden E (1974) On the theory and application of sum composition of latin squares and orthogonal latin squares. Pacific J Math 54: 85-112.