Biostatistics and Biometrics Open Access Journal

Review Article

Relationship for Quotient Moments of Ordered Random Variables from Exponentiated Pareto Distribution

Devendra Kumar*

Department of Statistics, Central University of Haryana, India

Submission: November 14, 2017; Published: May 22, 2018

*Corresponding author: Devendra Kumar, Department of Statistics, Central University of Haryana, India; Email: devendrastats@gmail.com

How to cite this article: Devendra Kumar. Relationship for Quotient Moments of Ordered Random Variables from Exponentiated Pareto Distribution. Biostat Biometrics Open Acc J. 2018; 6(5): 555698.DOI:10.19080/BBOAJ.2018.06.555698

Abstract

In this paper, we have established several new explicit expressions and recurrence relations satisfied by the quotient moments and conditional quotient moments of dual generalized order statistics from Exponentiated Pareto distribution, to enable one to evaluate the single and product moments of all order in simple recursive manner. The results for order statistics and record values are deduced from the relations derived. Further, recurrence relation for conditional quotient moments of dual generalized order statistics we obtain a characterization of exponentiated Pareto distribution.

Keywords: Dual generalized order statistics; Order statistics; Record values; Exponentiated Pareto distribution; Quotient moments; Recurrence relations; Conditional expectation; Characterization; Statistics; Reliability theory; Random variables; Probability density; Relations quotient; Continuous distribution; Explicit expressions; Recurrence relations; Recursive manner; Dual generalized; Pfeifer records; Framework; Cumulative distribution

Abbreviations: PDF: Probability Density Function; CDF: Cumulative Distribution Function; EP: Exponentiated Pareto

Introduction

The concept of generalized order statistics (^gos) was introduced by Kamps [1] as a general framework for models of ordered random variables. Moreover, many other models of ordered random variables, such as, order statistics, -th upper record values, upper record values, progressively Type II censoring order statistics, Pfeifer records and sequential order statistics are seen to be particular cases of These models can be effectively applied, e.g., in reliability theory. However, random variables that are decreasingly ordered cannot be integrated into this framework. Consequently, this model is inappropriate to study, e.g. reversed ordered order statistic and lower record values models. Burkschat et al. [2] introduced the concept of dual generalized order statistics (dgos). The dgos models enable us to study decreasingly ordered random variables like reversed order statistics, lower k-record values and lower Pfeirfer records, through a common approach below:

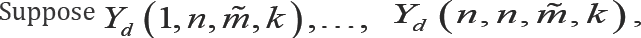
(k ≥ 1,m is a real number), are n dgos from an absolutely continuous cumulative distribution function (cdf) F (y) with probability density function (pdf) f (y), if their joint pdf is of the form

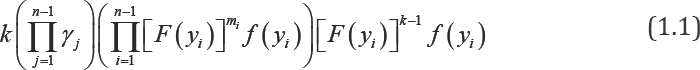
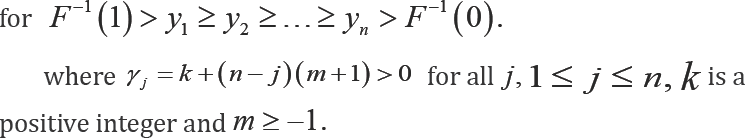
where 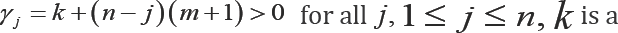isa positive integer and m ≥ — 1.

For convenience, let us define Y ( r, n, m, k) = 0. It can be seen that for 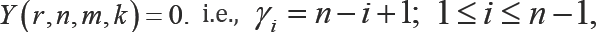we obtain the joint pdf of the ordinary order statistics. In the similar manner, choosing the parameters appropriately, some other models such as k^th lower record values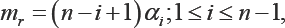 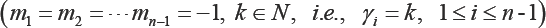sequential order statistic 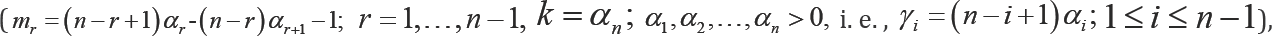order statistics with non-integral sample size 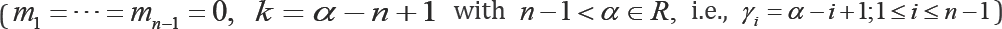[3,4] , Pfeifer's record values 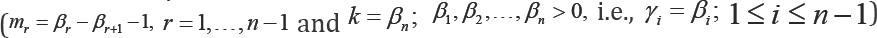and progressively type-II right censored order statistics 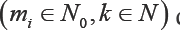can be obtained [5].

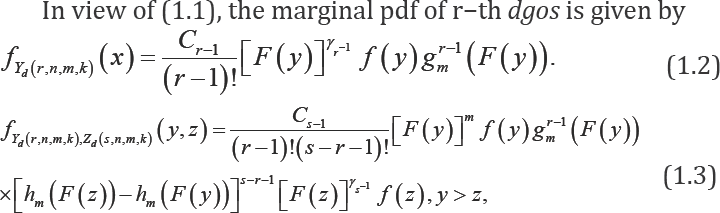
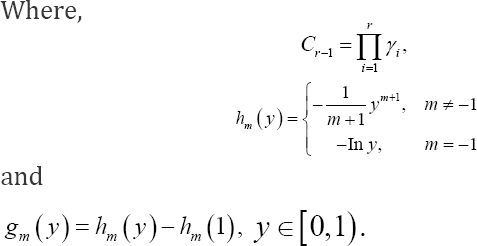
Several authors like Pawlas & Szynal [6], Ahsanullah [7], Mbah & Ahsanullah [8], Khan & Kumar [9,10], Kumar [11,12], Kumar [13] have done some work on dgos.

The exponentiated pareto distribution

The remaining ofthe article is organized as follows. In Section 2, the cdf and pdf of exponentiated Pareto distribution are explained along with some graphs at some particular values of parameters. In Section 3, we derive the relations for quotient moments of exponentiated Pareto distribution. We obtained relations for conditional quotient moments of from this distribution in Section 4. In last section of the paper we prove a characterization result on this distribution based on recurrence relation for conditional quotient moment of the dgos.

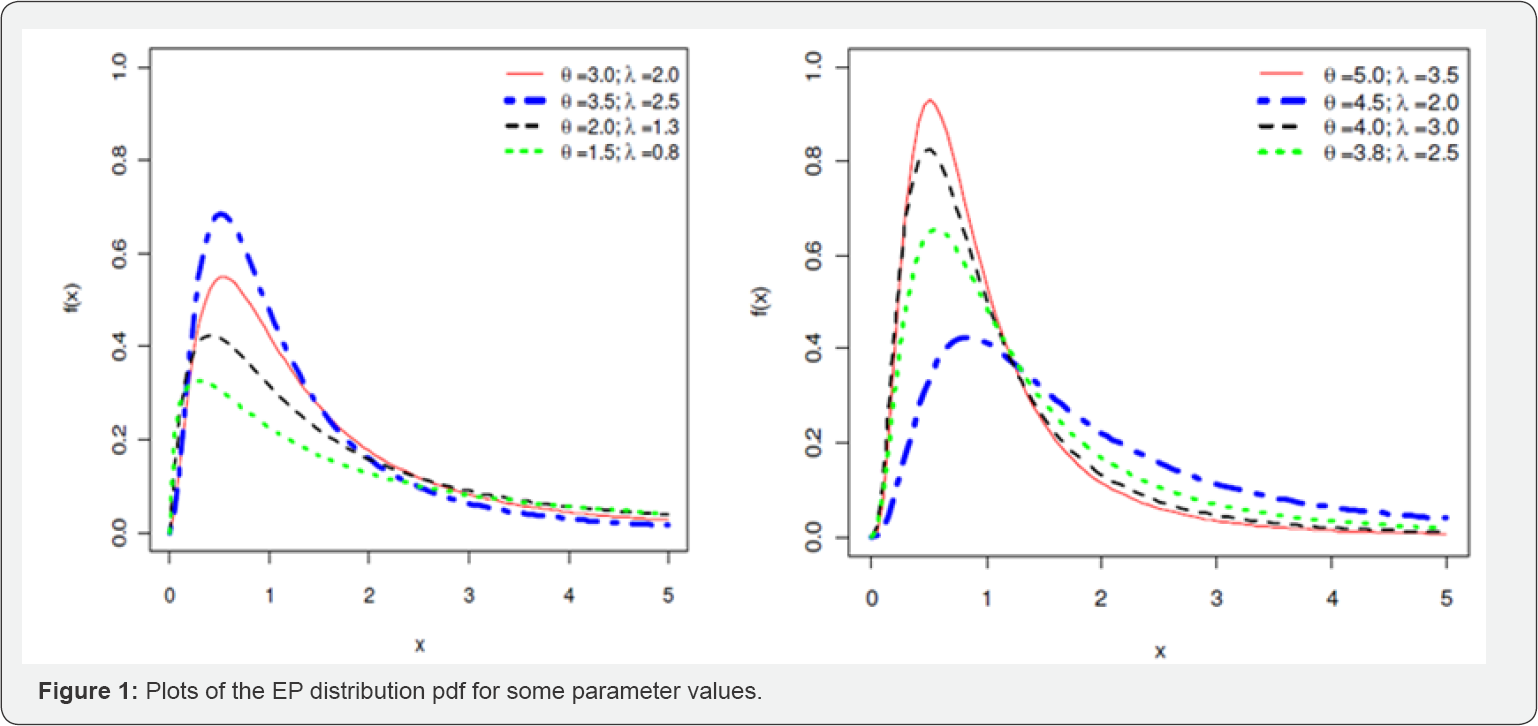
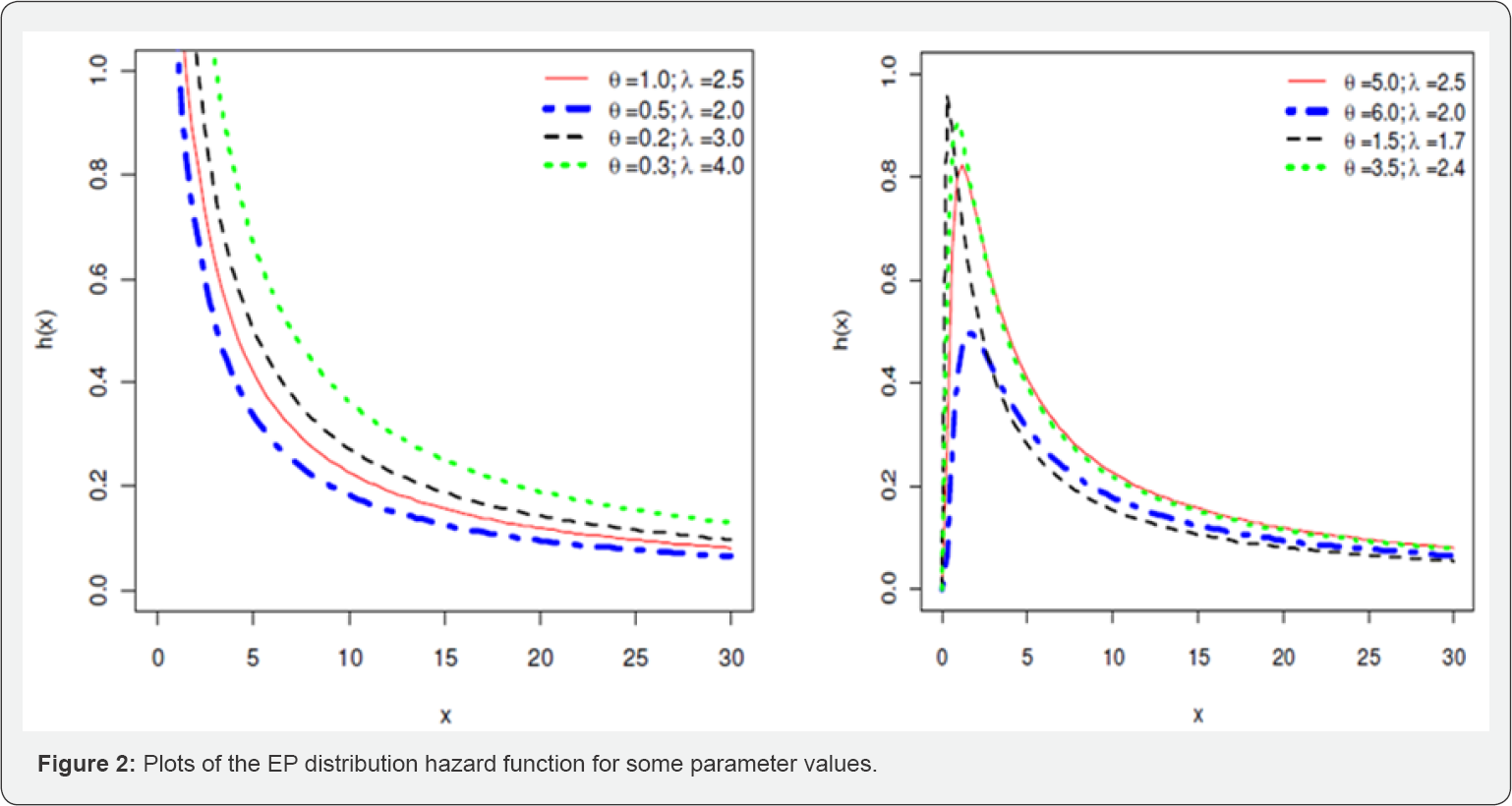
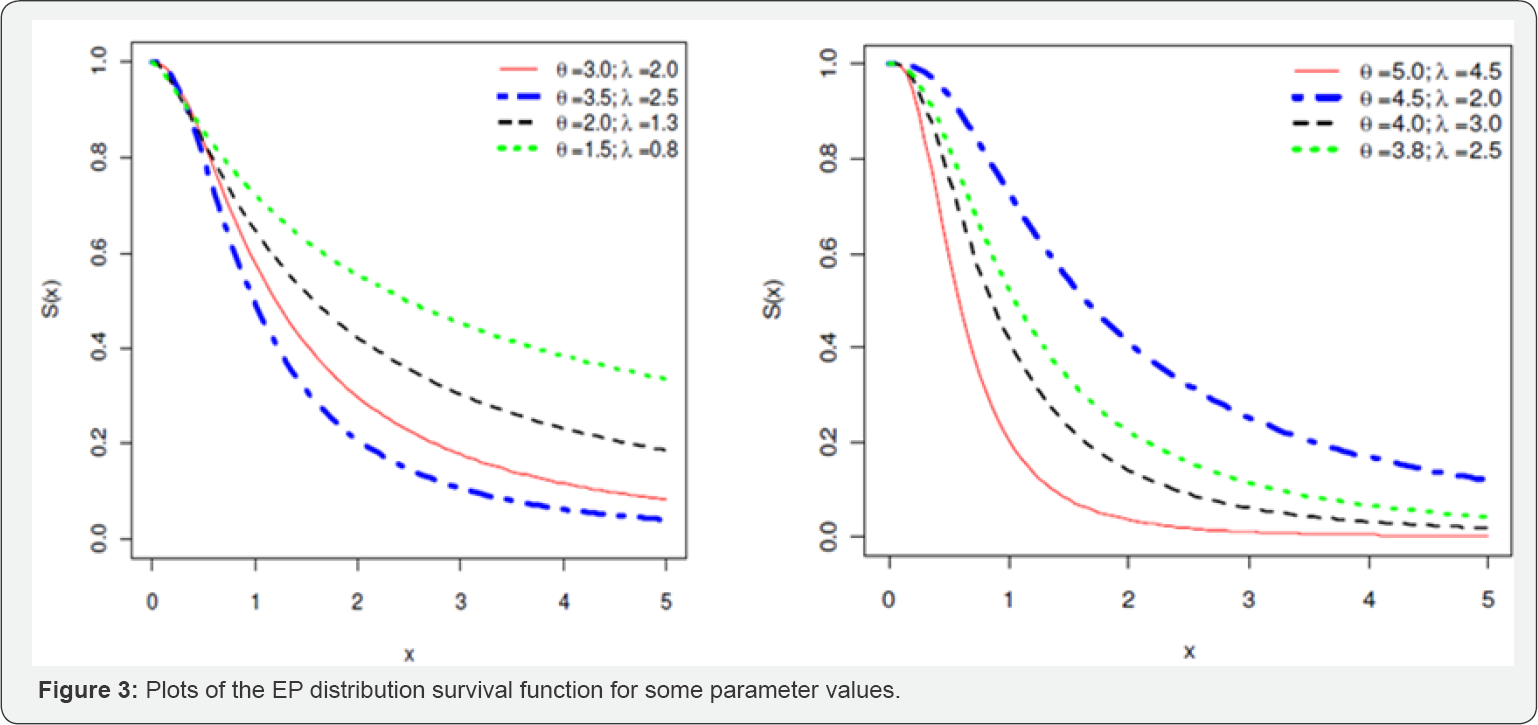
The remaining ofthe article is organized as follows. In Section 2, the cdf and pdf of exponentiated Pareto distribution are explained along with some graphs at some particular values of parameters. In Section 3, we derive the relations for quotient moments of expThe exponentiated Pareto (EP) distribution was first introduced in the literature by Gupta et al. [14]. The probability density function (pdf) is given by

One can observe from equation (1.1) and (1.2) that the characterizing differential equation for EP distribution is given by

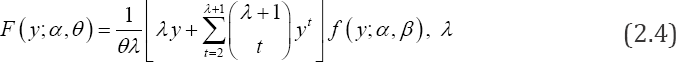
Where θ and λ are two shape parameters. When 0 = 1 the above distribution corresponds to the standard Pareto distribution of second kind [15] (Figure 1-3).

Relations for quotient moments of dgos

Lemma 3.1: For distribution as given in (2.1) and non-negative integers α, β, τ

Proof: From (3.2), we have

By setting in (3.4) and simplifying the resultant expression, we obtain the relation in (3.1).

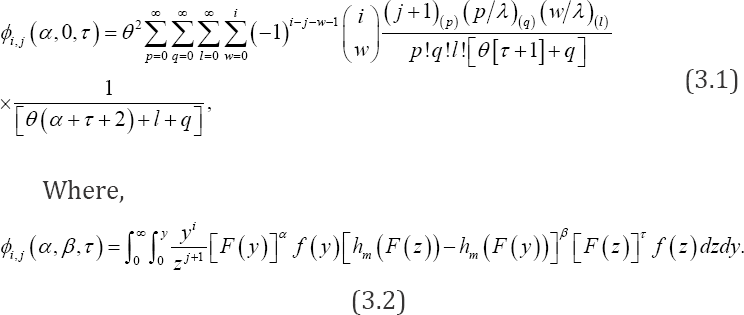
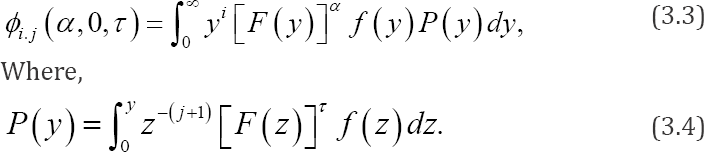
Lemma 3.2: For the distribution as given in (2.1) and any nonnegative integers and

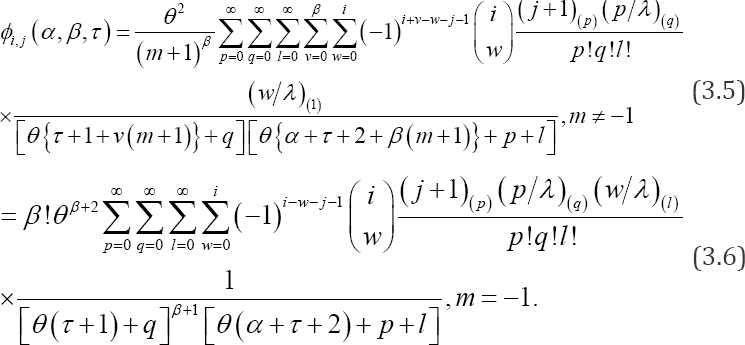
Proof: On using Lemma 3.1, we establish the result given in (3.5).

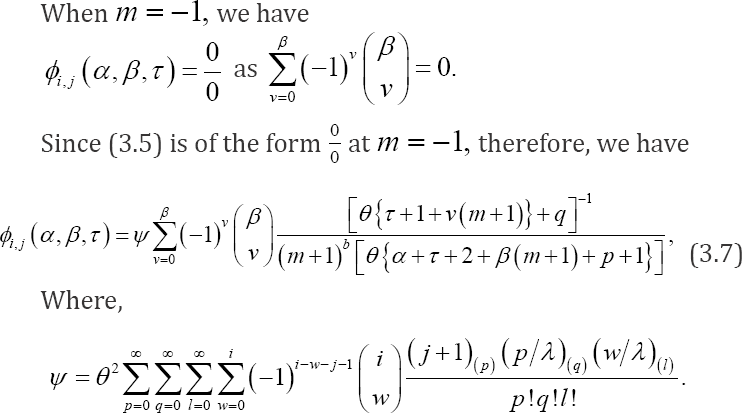
Proof The proof can be established on the lines of Lemma 3.2.

Remark 3.1: Under the assumption of Theorem 3.1 with m = 0, k = 1 we shall deduced the relations quotient moments of ordinary order statistics of the EP distribution.

Remark 3.2: Putting k = 0, m = —1 in Theorem 3.1 we obtain the relations for quotient moments of lower record values for EP distribution.

Integrating L (y) by parts and using (2.4) and substituting the resultant expression in (3.11), we get the result given in (3.10).

Remark 3.3: Under the assumptions of Theorem 3.2, with m = 0, k = we shall deduce the recurrence relations for quotient moments of ordinary order statistics from the EP distribution.

Remark 3.4: Putting k = 0, m = — 1 in theorem 3.2, we obtain the recurrence relations for quotient moments of lower record of the EP distribution.

Relations for quotient conditional expectation

Theorem 4.1: For the distribution given in (2.1) and for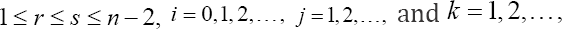

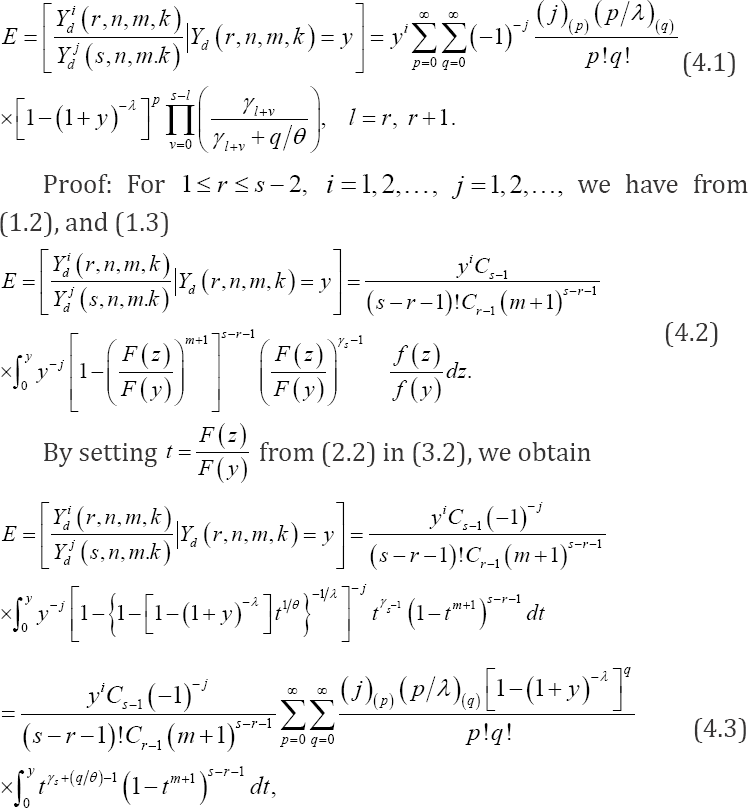
Again by setting w = t^m+ in (4.3) and simplifying the resultant expression, we get relation in (4.1).

Remark 4.1: Under the assumptions of Theorem 4.1, with m = 0, k = 1 we shall deduce the relations for conditional quotient moments of ordinary order statistics from the EP distribution.

Remark 4.2: Putting k = 0, m = _—1 in theorem 4.1, we obtain the relations for conditional quotient moment of lower record of the EP Pareto distribution.

Theorem 4.2: For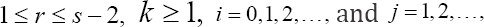

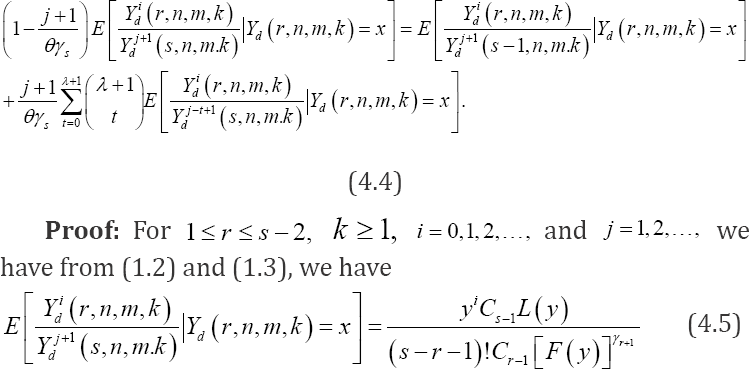
Substituting the value of L (y) from (3.12) in (4.5) and simplifying the resultant expression we get the relation in (4.4).

Remark 4.3: Under the assumptions of Theorem 4.2, with m = 0, k = 1 we shall deduced the recurrence relations for conditional quotient moments of ordinary order statistics from the EP distribution.

Remark 4.4: Putting k = 0, m = _—1 in theorem 4.2, we obtain the recurrence relations for conditional quotient moments of ower record of the EP Pareto distribution.

Characterization

Theorem 5.1: Let Y be a non-negative random variable having an absolutely continuous distribution function F (y) with F (0) = 0 and 0 < F (y) < 1 for all X > 0, then