Application of Penalized Mixed Model in Identification of Genes in Yeast Cell-Cycle Gene Expression Datas
Mojtaba Ganjali1,3* and Taban Baghfalaki2,3
1Department of Statistics, Shahid Beheshti University, Iran
2Department of Statistics, Tarbiat Modares University, Iran
3School of Biological Science, Institute for Research in Fundamental Sciences (IPM), Iran
Submission: January 23, 2018; Published: April 18, 2018
*Corresponding author: Mojtaba Ganjali, Department of Statistics, Faculty of Mathematical Sciences, Shahid Beheshti University, Tehran, Iran, Email: m-ganjali@sbu.ac.ir
How to cite this article: Mojtaba G, Taban B. Application of Penalized Mixed Model in Identification of Genes in Yeast Cell-Cycle Gene Expression Data. Biostat Biometrics Open Acc J. 2018; 6(2): 555682. DOI: 10.19080/BBOAJ.2018.06.555682.
Abstract
High-dimensional time-course gene expression data refer to time course data with a large number of covariates. In this status, variable selection is a popular approach for selecting important variables. In this paper, we review penalized likelihood mixed effects model for variable selection in high-dimensional time-course data. Then, the approach is used for variable selection in yeast cell-cycle gene expression data
Keywords: Gene expression data; Mixed effects model; Penalty function; Penalized likelihood; Time-course data
Introduction
Linear mixed effects models have been used in a variety of study to analyze data with between-subject dependence [1]. For example, in analyzing longitudinal data, clustered data, repeated measurements and spatial statistics mixed effects models are often used. In this structure, the linear predictor contains a Gaussian zero-mean latent variable in addition to fixed effects. This latent variable is called random effects and this kind of models which contain fixed and random effects are called mixed effects models. These models are usually used for analyzing correlated outcomes in studies with small number of explanatory variables. But, the use of this model becomes a major problem in a high-dimensional dimensional setting or when the purpose of the study is variable selection. When the number of fixed and random variables increases, because of complexity of mixed effects model, the inference about the model become challenging. Therefore, the selection of fixed or random effects is a key problem in this status. There are many traditional approaches for variable selection. For example, AIC, conditional AIC, BIC, Bayesian variable selection and so on [2-5]. Most of these approaches are based on computing a chosen criterion and finding a subset of variables as the best subset based on the chosen criterion. Among these approaches conditional AIC [6] and Bayesian variable selection are commonly used for variable selection in mixed effects model. Another approach which proposed for variable selection in mixed effect models is the use of penalized likelihood approach. Although the use of penalized likelihood for the high-dimensional regression model (when n ^ p ), which is famous to regularized regression method, is traditionally proposed [7,8]. But, nowadays the use of penalized likelihood for variable selection in mixed effects models is a popular approach [9-12]. In this paper, we review the ordinary penalized likelihood approach for variable selection in mixed effects model. Then, we use the approach for variable selection with lasso penalty for variable selection in yeast cell-cycle gene expression data set. This paper is organized as follows: in the next section penalized likelihood function for variable selection in mixed effects model is reviewed. The variable selection is given for yeast cell-cycle gene expression data in Section 3. The last Section includes some conclusions.
Penalized likelihood function for mixed effects model
In mixed effects model penalized likelihood function is usually used for both fixed and random effects. In the following, after introducing the notation used in this paper, at first penalized likelihood for fixed effects and then that for random effects are discussed.
Notation
Let there be N individuals in the study. Let yij, i = 1,..., N, j = 1,..., n be the response variable for the ith individual such that ith the individual has ni repeated measurements. Also, let xjj and zij be p x1 and q X1 vector of covariates. Also, we define n = ∑i=1nni to be the number of all observed responses in the study. In a matrix notation, we define yt =( yn, y yH), , x, =(x,1,..., xm_)' and Z, = (za,..., zn). In linear mixed effects model, the model can be written as follows:
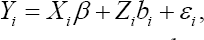
Where, β is a p x1 vector of regression coefficients,b, is a q x1 vector of random effects with b,~ Nq (0, D), ^ =(^1,...,^,) and ej ~N(0,ff2). Also, and b(i = 1,2,...,N) are independent. In a matrix notation, let y,b,e and X be matrices which obtained by stacking vectors of y,,b,s and X, respectively. Also, let Z = diag (Z1,..., ZN) and mA = dmg (D,..., D ) be a block-diagonal matrix. Then, the linear mixed effects model can be rewritten as
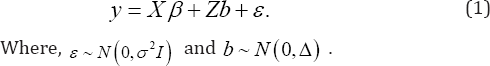
Selection of important fixed effects
The likelihood of marginal model (1) can be expressed as
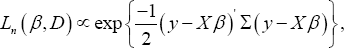
Where, dependence on sample size n is considered by adding the index n to L(.,.), also, 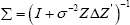 . To select the important covariates, the use of the following penalized log- likelihood function is used:
. To select the important covariates, the use of the following penalized log- likelihood function is used:
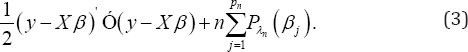
Where, P (.) is a penalty function with regularized parameter X In this notation, for showing dependence on sample size n the index n is used for X. Maximizing (2) is equivalent to minimizing
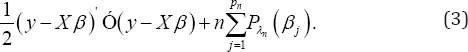
As mentioned before, Z depends on the unknown covariance matrix A and
Identifying important random effects
As mentioned by Fan & Li [12], the number of random effects q may be increased with sample size n so its dependency on n can be written by qn. The estimation and therefore identifying of random effects are different from fixed effects.One of the most famous approaches in estimating random effects is the empirical Bayes approach [14]. But, this approach is not useful for selecting random effects. In the following, we review the proposed method of Fan & Li [12] for identifying important random effects. Consider Ox = i-x(xx)‘x and a nx(n-p) matrix A such that AA = Ox. Let w= Ay, given the density function of w is given by
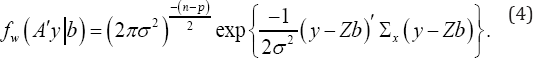
This conditional probability is independent of the fixed effects P and A As mentioned before b ~ N(0, A). Let A be the Moore-Penrose generalized inverse of A Then, a group variable selection strategy is needed to identify true random effects. For this purpose, consider the following regularization problem:
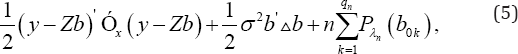
Where PX (.) is the penalty function with regularization parameter 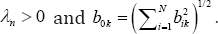 . Also, based on Theorem 2 of Fan & Li [12] the identified random effects is close to oracle estimator.
. Also, based on Theorem 2 of Fan & Li [12] the identified random effects is close to oracle estimator.
Tuning parameters selection
Different penalty function to achieve the purpose of variable selection in mixed effects models is proposed [10-17]. Some of the penalty function for variable selection in mixed effects models are lasso penalty function: 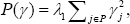 ridge penalty function:
ridge penalty function: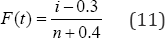 and elastic net penalty function:
and elastic net penalty function:
 In this paper, we use lasso penalty function and available lmmlasso in R for variable selection in time-course gene expression data [18]. One of the important stages in the used of the penalized likelihood function is the selection of the tuning parameter. The above-mentioned penalty function has some tuning parameter ( λ1,andλ2 ). A popular approach for selecting tuning parameter is based on some criteria such as AIC and BIC. In this framework, the selected tuning parameter is that with minimal AIC or BIC.
In this paper, we use lasso penalty function and available lmmlasso in R for variable selection in time-course gene expression data [18]. One of the important stages in the used of the penalized likelihood function is the selection of the tuning parameter. The above-mentioned penalty function has some tuning parameter ( λ1,andλ2 ). A popular approach for selecting tuning parameter is based on some criteria such as AIC and BIC. In this framework, the selected tuning parameter is that with minimal AIC or BIC.
Yeast cell-cycle gene expression data
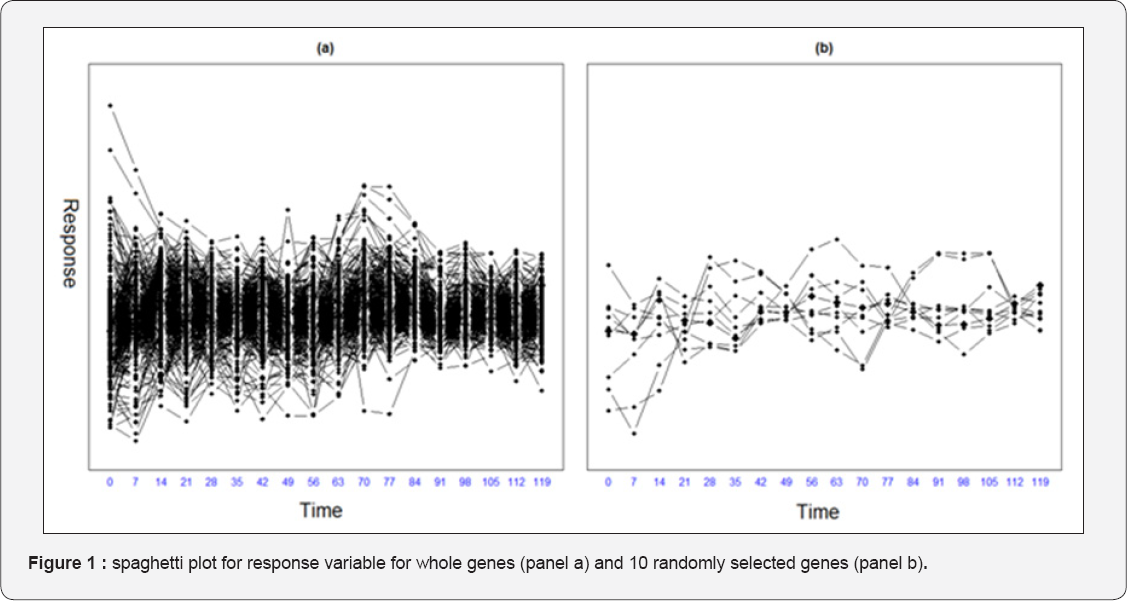
In this section, we use yeast cell-cycle gene expression data which collected in yeast cell cycle analysis project by Spellman et al. [19]. The goal of the project is to identify all genes whose mRNA levels are regulated by the cell cycle. The experiment recorded genome-wide mRNA levels for 6178 yeast ORFs at 7-minute intervals for 119 minutes which covers two cell- cycle periods for a total of 18 time points. Transcription factors (TFs) have an important role in gene expression regulation. Transcription factors are proteins involved in the process of converting, or transcribing, DNA into RNA. Transcription factors include a wide number of proteins, excluding RNA polymerase, which initiate and regulate the transcription of genes. We have extracted the cell cycle gene expression data of 542 genes from an α -factor based experiment. Each response variable corresponds to mRNA levels measured at every 7 minutes during 119 minutes (a total of 18 measurements). Also, we consider the ChIP-chip of the above-mentioned 106 TFs as explanatory variables. More information about this data set can be found in [20]. Figure 1 presents spaghetti plot for whole genes (panel penalized mixed model with 106 TFs as fixed effects with a random intercept and a random slop for time. Table 1 shows the 26 important covariates which selected using penalized likelihood mixed model by lasso penalty function. The tuning parameter is selected as \ = 3. Also, none of the random effects

Conclusion
In this paper, we review variable selection in mixed effects model using penalized likelihood approach. In this framework, we discussed how one can select fixed effects, random effects and tuning parameter. Also, in this paper, we consider lasso penalty function, also, we analyze a high-dimensional time course yeast gene expression data, where from 106 TFs, 26 of them were selected by the model to be important.
References
- Laird NM, Ware JH (1982) Random-effects models for longitudinal data. Biometrics 38(4): 963-974.
- Akaike H (1973) Information theory and an extension of the maximum likelihood principle. Selected Papers of Hirotugu Akaike 199-213.
- Liang H, Wu H, Zou G (2008) A note on conditional AIC for linear mixed-effects models. Biometrika 95(3): 773-778.
- Schwarz G (1978) Estimating the dimension of a model. The annals of statistics 6(2): 461-464.
- Chen Z, Dunson DB (2003) Random effects selection in linear mixed models. Biometrics 59(4): 762-769.
- Vaida F, Blanchard S (2005) Conditional Akaike information for mixed effects models. Biometrika 92: 351-370.
- Tibshirani R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1: 267-288.
- Zou H, Hastie T (2005) Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67(2): 301-320.
- Fan J, Li R (2001) Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American statistical Association 96(456): 1348-1360.
- Bondell HD, Krishna A, Ghosh SK (2010) Joint Variable Selection for Fixed and Random Effects in Linear Mixed Effects Models. Biometrics 66(4): 1069-1077.
- Ibrahim JG, Zhu H, Garcia RI, Guo R (2011) Fixed and Random Effects Selection in Mixed Effects Models. Biometrics 67: 495-503.
- Fan Y, Li R (2012) Variable selection in linear mixed effects models. Annals of statistics 40(4): 2043.
- Zou H (2006) The adaptive lasso and its oracle properties. Journal of the American statistical association 101(476): 1418-1429.
- Verbeeke G, Molenberghs G (2000) Linear Mixed Models for Longitudinal Data. Springer, New York, USA.
- Schelldorfer J, Bühlmann P, VAN S (2011) Estimation for High-Dimensional Linear Mixed-Effects Models Using l_1-Penalization. Scandinavian Journal of Statistics 38(2): 197-214.
- Hui FK, Muller S, Welsh AH (2017) Joint selection in mixed models using regularized PQL. Journal of the American Statistical Association 112(519): 1323-1333.
- Groll A (2011) glmmLasso: Variable selection for generalized linear mixed models by L1-penalized estimation. R package version 1(1).
- Schelldorfer J (2011) lmmlasso: Linear mixed-effects models with Lasso. R package version 0.1-2.
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, et al. (1998) Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell 9(12): 3273-3297.
- http://artax.karlin.mff.cuni.cz/r-help/library/spls/html/yeast.html






























