Improved EBLUPs in Mixed-Effects Regression Models
Sam W1, Peijin X2, Ching RY1 and Kelly HZ1
1Pfizer Inc., New York, USA
2Hershey, PA, New York, USA
Submission: October 23, 2017; Published:January 22, 2018
*Corresponding author: Sam Weerahandi, Pfizer Inc., New York, USA, Tel: 1-908-938-0927; Email: sweeraha@hotmail.com
How to cite this article: Sam W, Peijin X, Ching RY and Kelly HZ. Improved EBLUPs in Mixed-Effects Regression Models. Biostat Biometrics Open Acc J. 2018; 4(5): 555641. DOI: 10.19080/BBOAJ.2018.04.555641
Abstract
Mixed models are now heavily employed in business analysis, studies of public health, and in clinical research. However, widely used MLE based methods, the ML and the REML, for making inferences about the Best Linear Unbiased Predictor (BLUP) suffers from a number of drawbacks such as the non-convergence and lack of accuracy with small number of factor levels in a group structure. The BLUP in mixed models is a function of the variance components, which are typically estimated by MLE based method. Unfortunately, when the among group variance is small compared to the error variance, MLE either fails to provide any BLUPs or provides equal BLUPs for each level of a factor. Ironically this is exactly the situation where BLUP is considered most important. Therefore, the primary purpose of this paper is to overcome such drawbacks by developing a simple method for the widely used Mixed Models in a regression setting with a number of group structures among other covariates.
A simulated performance comparison is provided to show how the proposed method completely overcome the drawback while providing superior estimates in terms of MSEs.
Keywords: Variance components; Best linear unbiased predictor; Generalized inference; REML
Abbreviations: BLUP: Best Linear Unbiased Predictor; LSE: Least Squares Estimator; REML: Restricted Maximum Likelihood; ML: Maximum Likelihood; HB: Hierarchical Bayes; EB: Empirical Bayes; GE: Generalized Estimator; MC: Monte Carlo Simulation; MSE: Mean Squared Error; MCMC: Markov-Chain Monte-Carlo
Introduction
Lately mixed models are heavily used in a variety of applications, particularly in clinical research and in business analytics. For example, in multi-regional clinical trials with multiple doses, researchers usually compare the dose-response relationship for an efficacy or safety endpoint among the participating sites. Even if the parameter of dose-response is truly positive across all sites, we may still get negative estimates by chance in some regions due to small sample sizes. Such glitches occur due to small sample size, small number of factor levels, and large noise in data (making variance ratios small), precisely the situation Henderson [1] introduced the notion of the BLUP when he encountered such issues in animal breeding research. Another class of applications is analysis of promotional tactics, advanced analysts now use the BLUP (Best Linear Unbiased Predictor) more than the LSE (Least Squares Estimator).
In fact, the BLUP has become the most widely used statistical technique among business and market analysts in Corporate America using advanced statistical techniques. This is because the BLUP provides more reliable estimates (rather predictors) compared to the LSE, when one needs to quantify the impact of a promotional tactic by a number of customer segments or markets (e.g. DMAs), as it takes advantage of data from all markets as opposed to individual market's data that the LSE tends to depend upon. When one gets unrealistic estimates in above applications one can alleviate the issues with the same data when the problem is formulated in a mixed model setting by treating group effects as random effects distributed around the overall effect. For further discussion of underlying notions and the benefits of the BLUP in mixed models, the reader is referred to Searle et al. [2] & Robinson [3].
The main advantage of the BLUP over the LSE of classical regression is the greater accuracy of the former when inferences are made on a number of levels of a factor (e.g. markets, patient groups, and treatments) when the sample size is small or when the data are noisy. Due to this reason, mixed-effects models are now widely used in business and marketing analytics. In clinical research, they are heavily used in analyses of repeated measures [4-6].
Issues with existing estimation methods
The BLUP is essentially a weighted average of the mean effects of individual levels of a factor of interest and the overall effect of the factor, a shrinkage estimate. The weights of such shrinkage estimates is a function of variance components, which needs to be estimated. When the variance components are estimated by a certain method the result is referred to as estimated BLUP or empirical BLUP, and denoted as EBLUP. Widely used EBLUPs are the ML (maximum Likelihood) and the REML (restricted maximum likelihood) available form most statistical software packages.
The ML and the REML, suffer from a serious drawback, namely, for a fraction of possible values of the sample space, some of the variance component estimates obtained by such methods could become zero (or negative unless truncated), a highly undesirable feature. When running into this glitch, software tools such as SAS (e.g., the SAS procedure "proc mixed") or R (e.g., the R package "lme"), either complaint about non-convergence or produce variance components that are practically equal to zero. Rather than addressing the reality, some authors try to argue that such non-convergence occur due to zero variance components! In our simulation we will demonstrate that this happens when the among group variance is small relative to the error variance. When a variance competent representing the among group variance of a certain factor, EBLUPs of all levels of that factor become equal, a highly undesirable property. Even if they yield positive variance components and there is no convergence issue, the MLE based methods tend to be less accurate, say in terms of the MSE performance when the among group variance is small compared to the error variance, as shown by Yu et al in ANOVA type models.
Resolving the issues
So, the primary purpose of this article is to develop an estimation method that does not suffer form the problem of zero variance components that MLE based methods often run into. For the balanced ANOVA case, Yu et al. [7] proposed a method that does not suffer from that drawback. In this paper we will extend their method for any number of groups structures in a regression setting. While the Bayesian approach also can assure positive variance estimates, the proposed approach does not require one to specify prior distributions or deal with hyperparameters.
By taking the Bayesian approach, One may also avoid such issues by taking the empirical Bayes (EB) and Hierarchical Bayes (HB) approaches, as studied by Ghosh & Rao [8]. The reader is referred respectively to Harville [9], and Datta and Ghosh [10] for details about EB and HB, as they cover much of the prior work taking the Bayesian approach to the problem. Ghosh and Rao [8] and Rao [11] studied these EBLUPs along with a number of other EBLUPs in the area of small area estimation and reported that EB and HB tend to perform better than other EBLUPs available in the literature, and so in our performance comparison in Section 4 we will compare the EBLUP proposed in this article against EB and HB as well. As Ghosh & Rao [8] correctly pointed out, small area models are special cases of the general linear mixed model involving fixed and random effects, and so in this study we will take the latter approach, which is now widely employed.
The BLUP in Regression Setting
Consider a regression in a mixed model setting with a number of group structures. In this article we confine our attention to the variance structure that is the most widely used by practitioners and the default setting in all widely used statistical software packages. To be more precise, consider the mixed model with J sets of random effects
y=Xβ+Z1u1+Z2u2,---,+ZJuJ+ϵ, (1)
Where, X is an Nxk matrix formed by a set of covariates corresponding to k fixed effects â,Zj are N X kj. matrices formed by covariates corresponding to random effects uj of jth factor with ki levels, ϵ∼N (0,σe2 )and Uj ∼N (0,σe2 ) , and j = 1, ..., J are assumed to be distributed independently. In formulating the model, the vector of fixed effects β should include the overall mean effect of each of the factors, which we denote as μi, j =1 ... J The problem of primary importance in most practical applications, described in the introduction, is the estimation of the BLUPs, èi=ìi +E(Ui| y) = ìi + ũi,J=1 Of course, the model can be written in familiar compact form as
y=Xβ+Zu+ ϵ, (2)
Where, Z = (Z1, .... ,ZJ) and U= (u1, .... ,uj). Henderson [1] provided the formula to the BLUP of random effects and the BLUE to the fixed effects when the variances are known. Robinson [3] showed that various derivations available in the literature all lead to Henderson's formulas
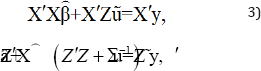
Where, Σ= Var (u). In our problem, which is also the default in statistical software packages,
Σ = diag (ρ1I1, ρ2I2, ..., ρJIJ), where ρj= ρj2 /ρe2. The equations in (3) can be solved explicitly for 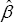 and û. It is evident from (2)
and û. It is evident from (2) 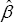 that should be the GLSE
that should be the GLSE
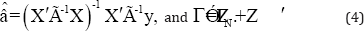
Indeed, Henderson et al. [12] showed that the solution of (3) for is the GLSE. Then, we can easily obtain the explicit solution for the random effects as
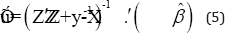
Estimating the BLUPs
In practice, however the variance components are unknown, and needs to be estimated. They are easily estimated by the REML or the ML methods. The issue however, is that the variance ratios required in applying above formula become 0 for a fraction of possible values of the sample space, as practitioners frequently encounter, when the error variance is large compared to the factor variance, exactly the situation for which BLUPs are useful in the first place. Now consider the problem of avoiding the above drawback of MLE based methods so that BLUPs of levels of any factor will not degenerate at overall factor effect for any set of data. For the case, Weerahandi [13] used distributional results derived by Wald (1974) in point estimation of the factor variance and Gamage et al. [14] used the results in developing prediction intervals for the BLUP. Now, in order to derive an appropriate distributional result in point estimation of variance components for any a number of factors by taking Yu et al. [7] approach, let us derive the distribution of , the LSE (the Least squares Estimator, as opposed to the Henderson's predictor ) of , regardless of the value of by taking Wald (1974) type argument.
Distributional results
To develop necessary distributional results to tackle a particular variance component of interest, in a setting which is somewhat more general than required here, consider the mixed effects model
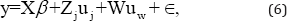
Where all terms are as defined as before, except that we allow the covariance matrix of the random effects vector uw to be distributed as uw˜N(0,∧). As in Seely and El- Bassiounni (1983), we allow ∧ to be a completely arbitrary covariance matrix, except that it has a positive definite submatrix, whereas the random effects of particular interest is distributed as úiI (0 2ij ) independently of uw. To take the approach similar to that used by Wald (1947) to derive necessary distributional results, let us momentarily treat and as fixed effects, an assumption that we will drop later. Here we need distributional results in a form somewhat different form that developed by Seely and El-Bassiounni (1983).
To carry out the alternative derivation, first of all, it should be pointed out that the LSE formula used by computer algorithms of statistical software is not the familiar one given in texts books,
but rather the one based on QR the decomposition, which is fool-proof in that the matrix of comparatives does not necessarily have to have full rank. In our application the matrix of covariates
is 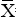 = (X,Zj W) and the LSE formula used by computer
algorithms is not (
= (X,Zj W) and the LSE formula used by computer
algorithms is not (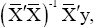 but rather a formula based on the QR decomposition. The decomposition starts with the
partition
but rather a formula based on the QR decomposition. The decomposition starts with the
partition 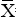 =QR=(Q1Q2)(R1,0) with orthogonal matrices Qs and upper triangular matrices ,Rs and 0 is a РxР matrix of to start with, where Р is the number of columns of .
=QR=(Q1Q2)(R1,0) with orthogonal matrices Qs and upper triangular matrices ,Rs and 0 is a РxР matrix of to start with, where Р is the number of columns of .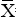 When
When 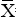 is not of full rank, algorithm drops columns of R1 corresponding to zero vectors Q1 and is re-adjusted. Then, in terms of final Q and R terms, the formula underlying the LSE algorithm is (R1')-1Q1'y, where R1 is a q x q matrix and Q1 is an ,Nxq and q=rank(
is not of full rank, algorithm drops columns of R1 corresponding to zero vectors Q1 and is re-adjusted. Then, in terms of final Q and R terms, the formula underlying the LSE algorithm is (R1')-1Q1'y, where R1 is a q x q matrix and Q1 is an ,Nxq and q=rank(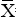 ) The residual of the regression is given by e=Q'2'Q2y.
) The residual of the regression is given by e=Q'2'Q2y.
For notational convenience, and to use text book formulas, let, 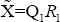 a full-rank sub-matrix
a full-rank sub-matrix 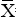 , something a user can get after observing a computer output even if he/she runs the regression blindly. Let be the vector of random
corrsponding to final LSEs
, something a user can get after observing a computer output even if he/she runs the regression blindly. Let be the vector of random
corrsponding to final LSEs
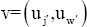
I. Lemma 1
The distribution of the LSE of uj when run in an ordinary linear regression setting is given by
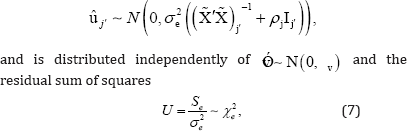
Where, uj, is the a jx1 sub-vector of ûj corresponding to the non-na LSE estimates, ρ=σj2/σe2 ,aj = rank(Zj), and
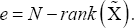
II. Proof
Consider the ordinary regression of y on Ẋ=c(X,Z,W) if us were fixed effects. Then, using Waldˇ¦s argument with milder regularity conditions, Seely and El-Bassiounni (1983) showed that the unconditional as well as the conditional distribution of the error sum of squares given is given by
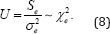
Moreover, from the theory of regression it also follows that the unconditional as well as the conditional distribution of

Along with (7), It should be emphasized that S (ρ) is
computed only with a j LSEs that the QR algorithm yielded. In this computer age there is no real need of special methods to compute matrix inverses such as the above, but obviously we
can increase the accuracy by diagonalizing the 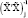 -1 matrix by means of an orthogonal matrix, say p, so that the sum of squares
-1 matrix by means of an orthogonal matrix, say p, so that the sum of squares
term S(ρ) can be further reduced to
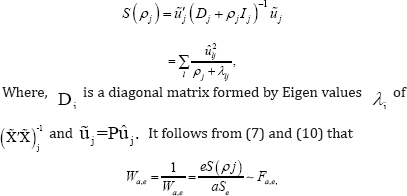
Where, α = Aj. As in Yu et al. (2014) we can avoid negative variance components by defining Generalized Estimators such
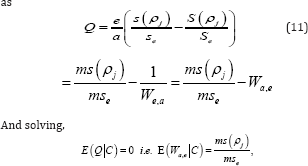
where upper case quantities denotes random quantities and lower case quantities stand for there values at observed samples, and C is a condition to assure that solution of (11) for ρj is positive for all possible sample points. They also showed that the condition is met when Wa,e >mse/,ms0(equivalently ,Wa,e >mse/,ms0,wherems0=ms(0)Hence, as in Yu et al. (2014), we can obtain a generalized estimator (GE) that does not suffer from the above mentioned drawback as follows:
o Generate large number of random numbers from W ˜Fa,e.
o Discard the random numbers that do not meet the condition W < ms0mse
o Find the conditional expectation EC = E (W|C) based on the W Samples meeting the condition.
o Estimate ρj
as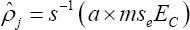
o By using a root finding algorithm to solve the equation s (ρj)a x mseEc
o Estimate the BLUP by applying (5) equation with 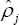 in place of ρj
in place of ρj
It should be emphasized that the merit of a statistical procedure should be judged by it performance compared with available competitors, and not by the nature of the notions, methods used, or the popularity of the author who introduced such notions. Therefore, in Section 4 we will demonstrate the superiority of the EBLUPs proposed via a simulation study.
The BLUP in unbalanced one-way ANOVA
The purpose of this section is to provide explicit formulas for the EBLUPs in unbalanced ANOVA, which is a particular case of special interest. To do so, consider the simplest unbalanced random-effects model,
Yi,j = μ + τj+ ϵi,j, i=1,2, ,...,k and j = 1,2,...,ni
Where, μ is a fixed effect; τj is a random effect distributed τj ˜N(0,σ2τ);ϵi,j N(0,σ2e)k is the number levels of a factor, and ni > is the number of observations from subjects in
group i. Let 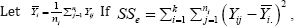 then
then  Define a set of weights as wi = i (ρ) = ni/i + niρi where
ρ = σ2τ/σ2e is the ratio of the two variance components. To give specific formula for the BLUP and the EBLUP in the ANOVA case, define
Define a set of weights as wi = i (ρ) = ni/i + niρi where
ρ = σ2τ/σ2e is the ratio of the two variance components. To give specific formula for the BLUP and the EBLUP in the ANOVA case, define
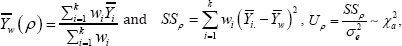
Where, α = k -1 In the ANOVA problem the desired BLUP for group 1 has the simple form
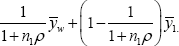
Since the variance ratio is typically unknown, consider the problem of finding an EBLUP while assuring the positivity of the weight θ = 1/ (1 + ni ρ). In the ANOVA problem, since we have a simple formula for the weight playing the shrinkage role in the BLUP, we can treat θ as the parameter of interest. Taking the approach in the previous section, we can use the distributional result,
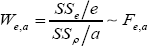
To obtain the appropriate generalized estimator. Since we need to estimate p in such a way that the estimator of 0 will close to being an unbiased, we can obtain the counterpart of Yu
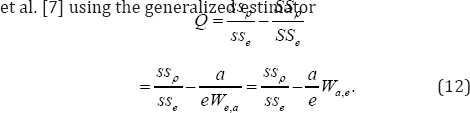
As in Yu et al. [7], the appropriate estimator of the parameter θ can be derived by taking the unconditional expectation of the Q. Since the observed value of Q is 0, the corresponding generalized estimator (GE) for θ is obtained by equating its expected value to θ, and then solving the equation for β as Weerahandi [13] suggested. The estimators of θ and ρ are obtained in this manner are
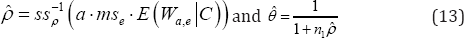
Where, C is a condition suggested by the known properties of the parameters and ssp-1. is the inverse function of .sspNoting that when ρ=0, SSp reduces to the simple unweighted among group sum of squares, as Yu et al. [7], we can assure the positivity of the ρ parameter and non-negative weights appearing in the BLUP formula by taking the condition of C to be We,a ≥ w, where w = mse msa where mse = ss e/e and msa = ssa/a. The e ei a at superiority of the resulting estimator will be demonstrated in Section 4 via a simulation study.
Illustration and simulation results
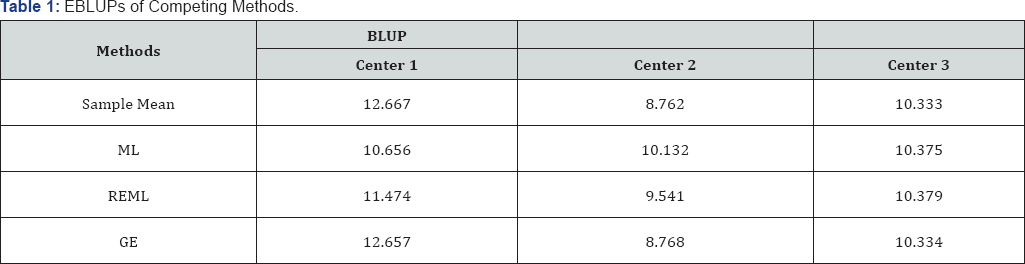
Dental Caries example in one-way layout: We illustrate our proposed method using an example in dental research, with publicly available data. Before we undertake a simulation study in the next section the purpose here is to show the difference in estimates in a qualitative manner. The example is based on the data from Stokes et al. [15] involving 3 treatments. The full data set from 69 female children from 3 centers may be found in Stokes et al. [15] SAS manual (http://ftp.sas.com/samples/ A55320). The purpose is to show the difference in competing estimates that indicates a drawback of MLE based methods. This real data example involves three treatments, including stannous fluoride (SF; n1 = 22), acid phosphate fluoride (ACT; n2 = 27), and distilled water (W;n3 = 20). The numbers of decayed, missing, or filled teeth (i.e., DMFT) are examined before vs. after respective treatments. The post DMFT assessments are analyzed as the response variable and the treatment comprising fixed effects, and centers comprising random effects. Notice that, despite the fair amount of variation in the sample means, the ML has shrunk the estimates too much to yield EBLUPs, which are practically equal.
This is a repercussion of the underlying asymptotic method yielding the among center variance to be almost zero, It should be mentioned that in some applications the variance estimator given by the ML becomes exactly zero for a fraction of possible sample points. In regional trial this amounts to concluding that efficacy of a treatment by region are all equal despite genetic differences and patient population in different regions, when it is in fact an artifact of an assumption underlying the ML, namely the assumption that the number of levels of the factor under study is large. The REML estimates are slightly better than those by the ML estimation method, but in this example where there is only 2 degrees of freedom to perform inferences on the factor variance, it has also relied upon the three data points too much. The shrinkage given by the GE is rather small, thus not depending on the unreliable factor variance estimate. Yet one may argue, which one is better or more reliable. Therefore, next we perform more extensive simulations, which can shed further light on true performance of competing methods, and to show that GE is superior in all scenarios we studied.
Simulation studies
The purpose of this section is to conduct a Monte Carlo simulation (MC) study to establish that not only the proposed estimator GE overcome the zero variance estimation problem of MLE based methods, but also it is superior in terms of the MSE performance. The study is carried out by generating simulated data from exact assumed distribution, and then computing the Mean Squared Error (MSE) for group 1 (as an example) in the repeated sampling (MC=1000 iterations). We assume two sets of unbalanced mixed models. The first study involves an one-way layout with unequal sample sizes {5’l0,l0,l5}. The second study involves a regression model with number of groups ranging from 3 to 10, which covers typical applications.
One-way layout setting
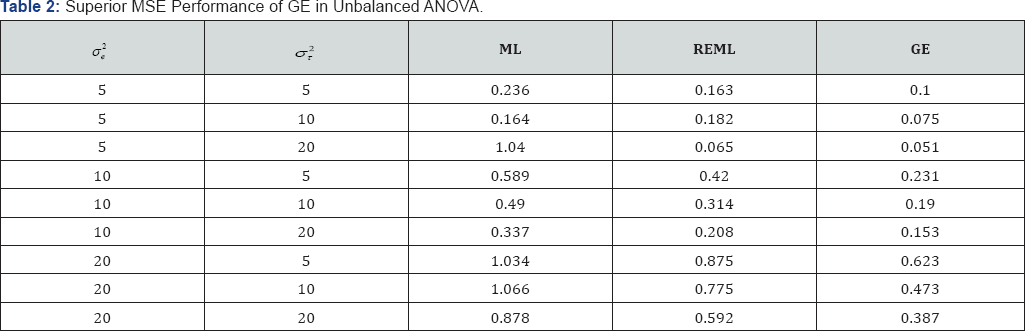
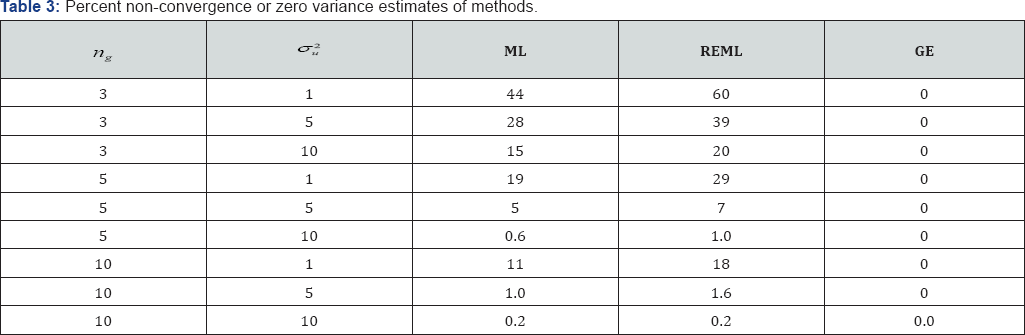
The MSEs of competing methods are calculated when the error variance vary around the factor variance. The value of the parameter, μ does not drive the MSE performance, but in our study it was set at 10. Table 1 below shows the values of the two sets of variances considered along with the MSE of the BLUP of first group estimated by each method. It is evident from Table 2 that the MSE performance of GE is substantially better than that of the ML and the REML. The ML has the worst MSE performance, and the GE is the best in all cases.
In our simulation study of the regression case, we considered 3; 5, and 10 groups. Since we can hardly learn anything new from regression models involving number of factors, a regression model with one group structure is considered. Since the issue with asymptotic methods underlying the MLE based methods is the number of groups rather than the sample size from each group n, it is set at 10. Since the ratio between the factor variance and the error variance mainly drive the issue of 0 variance with MLE based methods, σ2 was fixed at 20 and σ2 at typical values in applications where the BLUP is preferred over the LSE. Here we used the MSE of competing methods to evaluate the performance of each methods as the factor variance vary in a practical range of BLUP applications. The value of the intercept of the regression does not impact the MSE performance, but in our study it was set at 100, and a continuous covariate is include and set at random normal numbers generated with mean 0 and variance 0.05.
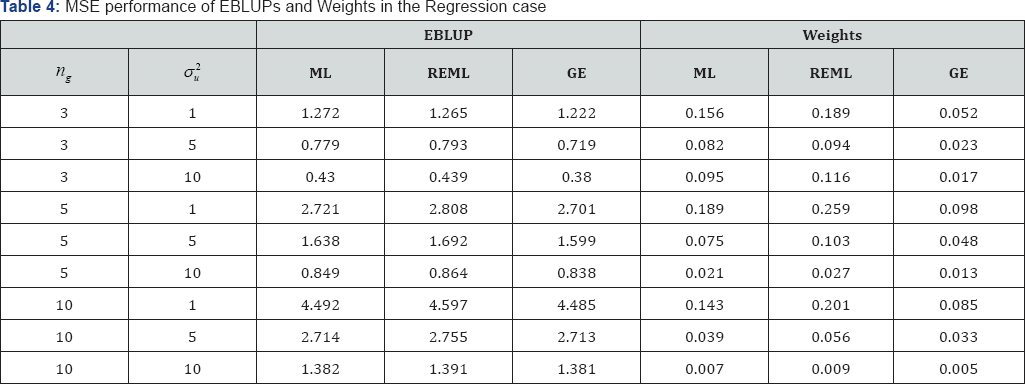
Occurrences of zero variance estimation are also studied. Table 3 below shows the percent zero variances yielded by each method, and Table 4 shows the values of the MSE by each method It is evident from Table 3 that, when among group variance is small compared to the error variance, MLE based methods have serious issues due to yielding zero variance components thus leading to equal EBLUPs for all factor levels, where as the GE method has completely overcome the drawback. Again, Table 4 shows that the MSE performance of GE based EBLUP is better than that of ML and REML. As before the ML tend to have the worst MSE performance, whereas GE is the best in all cases. Especially when the likelihood function get maximized at negative values of the variance component, ML and REML simply truncates the estimated variance to zero. Moreover, unlike in ANOVA, MSE performance of EBUPs can vary depending on the covariates of the regression model. Therefore, also reported in Table 4 is the MSE performance of estimated values of a weight, defined as
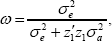
Where, σ2a is the factor variance and z1 is the vector of covariates corresponding to the group 1. The weight ω is closely related to the extent of shrinkage given by competing methods, compared the actual shrinkage of the EBLUP
Performance comparison in small area estimation
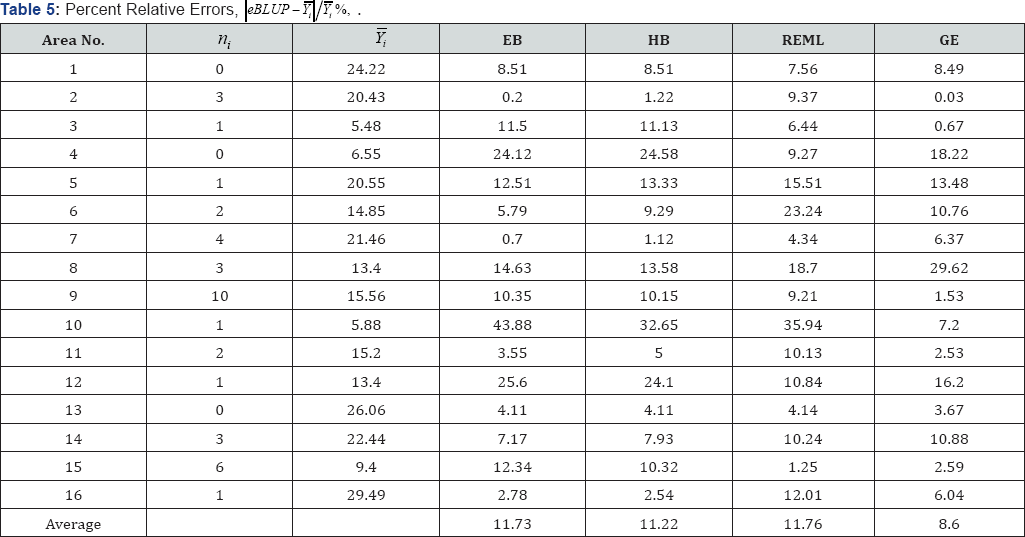
The purpose of this section is to study the performance of EBLUPs discussed by Ghosh and Rao [8] and Rao [11] in the application of small area estimation. In their study, the empirical Bayes (EB) estimator suggested by Harville [9] and Hierarchical Bayes (HB) estimator of the BLUP suggested by Datta & Ghosh [10] were found to outperform other competitors in the area of small area estimation, and so here we only study the performance of the EB and the HB compared with the GE and the REML, which were found to perform better than the ML in our study above. We used the same data set that Ghosh & Rao [8] reported and used the same diffuse prior of Datta & Ghosh [10]. The findings of the study are reported in Table 5. Denoted by ni is the sample size of area i, and Ȳi s the observed response mean of area i. The performance of each EBLUP is judged by its capability to predict mean response based on the values of the covariates reported in Ghosh & Rao [8]. Table 5 shows relative absolute errors, the absolute deviations of the predicted values from the response means, and the performance of each is judged by its average for all areas. It is evident from the table that the GE derived in this article has outperformed all competing estimators. As Ghosh & Rao [8] also reported, the EB and the HB has a slight advantage over the REML.
Concluding Remarks
At a time when, mixed models have become highly popular in a variety of applications ranging from market analysis to clinical research, we have considered a problem of immense importance, namely the problem of obtaining more accurate EBLUPs than those provided by likelihood based methods. For a wide array of applications consisting of small samples or few groups, as well as large samples with high variability, we have provided a class of estimators that are substantially superior to the ML and the REML in terms of the convergence without zero variances and the MSE performance. In this article we have derived superior estimators for the cases of unbalanced one-way layout and regression mixed models involving any number of random effects with compound symmetric covariance structures. It is useful to extend such results to more complicated mixed models and other widely used covariance structures, and so further research in this direction is encouraged. For balanced ANOVA models, Weerahandi & Ananda [16] obtained further improvements than the type of estimators considered in this article and Bayesian estimators with non-informative priors. Extending their results to unbalanced cases is a non-trivial task, and also requires further research [17-19].
One may avoid drawbacks of the ML and the REML by taking the Bayesian approach. But in taking the Bayesian approach, one has to specify prior distributions and hyper-parameters. Moreover, in Bayesian estimation using such algorithms as MCMC (Markov-Chain Monte-Carlo) could be time-consuming and could yield estimates which are highly sensitive to the choice of the family of priors and the choice of hyper-parameters, especially when there are a large number of model parameters. The approach proposed in this article does not suffer from such drawbacks. Moreover, the EBLUP proposed in this article, namely the GE, was also found to be better than Bayesian estimators EB and HB requiring no proper priors. Further research is also necessary to obtain more powerful tests of hypotheses of BLUPs than those available in the literature. By taking the generalized approach, Gamage et al. [14] obtained prediction intervals for BLUPs, which are superior to the MLE based methods in terms of intended coverage. The coverage of such prediction intervals may still be improved upon by taking advantage of the knowledge of the parameter space of the variance ratios, as proposed in this article.
Acknowledgment
The authors would like to thank Professor Charles McCulloch for checking the Lemma of the paper to see if there are any obvious errors.
References
- Henderson CR (1975) Best linear unbiased estimation and prediction under a selection model, Biometrics 31(2): 423-447.
- Searle SR, Casella G, McCulloch CE (2006) Variance Components Wiley, Hoboken, New Jersey
- Robinson GK (1991) That BLUP is a good thing: the Estimation of random effects. Statistical Science 6(1): 15-32.
- Gurka MJ, Edwards LJ, Muller KE (2011) Avoiding bias in mixed model inference for fixed effects. Stats Med 30(22): 2696-2707.
- Littell RC, Pendergast J, Natarajan R (2000) Modeling covariance structure in the analysis of repeated measures data. Stat Med 19(13): 1793-1819
- Frison L, Pocock SJ (1992) Repeated measures in clinical trials: analysis using mean summary statistics and its implications for design. Stat Med 11(13): 1685-1704.?
- Yu CR, Zou K, Carlsson M, Weerahandi S (2015) Generalized estimation of the treatment effects in mixed-Effects models: A Comparison with ML and REML. Communications in Statistics (S&C) 44(3): 694-704.
- Ghosh M, Rao JNK (1994) Small area estimation: An appraisal. Statistical Science 9(1): 55-93.
- Harville DA (1990) BLUP and beyond. Advances in Statistical Methods in for genetic Improvement of Livestock 18: 236-239.
- Datta GS, Ghosh M (1991) Bayesian prediction in linear models: Applications to small area estimation, Annals of Statistics 19(4): 17481770.
- Rao JNK (2003) Small Area Estimation. Wiley, Hoboken, New Jersey
- Henderson CR, Kempthorne O, Searle SR, Krosigk CN (1959) Estimation of environmental and genetic trends from records subject to culling, Biometrics 13: 192-218.
- Weerahandi S (2012) Generalized point estimation, Communications in Statistics (T&M) 41(22): 4069-4095.
- Gamage J, Mathew T, Weerahandi S (2013) Generalized prediction intervals for BLUPs in mixed models. Journal of Multivariate Analysis 220: 226-233.
- Stokes ME, David CS, Koch GG (1995) Categorical Data Analysis using the SAS System. SAS Institute: Cary, NC.
- Weerahandi S, Ananda M (2015) Improving the estimates of BLUPs of mixed-effects models. Metrika 78(6): 647-662.
- Borrell LN, Talih M (2011) A Symmetrized Theil index measure of health desparities: An example using dental caries in U.S. children and adolescents. Stat Med 30(3): 277-290.
- Tsui K, Weerahandi S (1989) Generalized p-values in significance testing of hypotheses in the presence of nuisance parameters. Journal of the American Statistical Association 84: 602-607.
- Weerahandi S (2004) Generalized Inference in Repeated Measures: Exact Methods in MANOVA and Mixed Models. Wiley, Hoboken, New Jersey.






























