Dike Chukwudi Henry

doi:10.19080/ASM.2019.03.555603

Case Report

Empirical Approach of Leading the Academic Advising Process in Higher Education

Saeed Hameed Aldulaimi*

¹College of Administrative Sciences, Applied Science University (ASU), Bahrain

Submission: December 12, 2018; Published: January 03, 2019

*Corresponding author: Saeed Hameed Aldulaimi, College of Administrative Sciences, Applied Science University (ASU), Bahrain

How to cite this article: Saeed Hameed Aldulaimi. Empirical Approach of Leading the Academic Advising Process in Higher Education. Ann Soc Sci Manage Stud. 2019; 2(4): 555603. DOI: 10.19080/ASM.2019.03.555603

Abstract

Network effect and systemic properties of financial systems have become an increasingly useful tool in accessing financial stability, predicting failures as well as making vital policies. This work theoretically accesses behavioral qualities of the standard Eisenberg & Noe [1] model as it attempts to capture systems involving systemic risk. This work observes the algorithm proposed and help provide clarification as on its ability to model financial systems facing danger of systemic risk.

Mini Review

In context of financial systems and their workings, definitions of systemic risk as well as financial contagion seems relatively vague and easily interchanged with one another. However, Zigrand [2] provides a valuable definition where he identifies systemic risk as the probability of an adverse event leading to a breakdown of an otherwise functioning system. At its core level, systemic risk is caused by systemic events and these events are such that their effect is in greater magnitude to a financial systems performance as the original event would have suggested. Hence, while contagion captures spillover effects of an exogenous shock to a node on another connected node, systemic risk examines a more extreme case where the bank the shock originates from feel some residue having been, to some degree, neutralised by other interconnected nodes. Therefore, a lot of financial systems researchers including Eisenberg and Noe, Demange, Zigrand [1-3] as well as Henry [4] all attach the concept of systemic risk to Feedback loops. And the idea of loop suggests cyclical obligations (Figure 1).

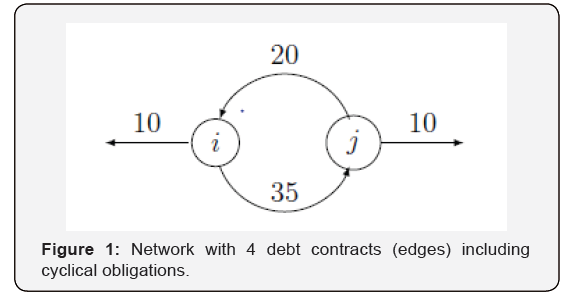
To elaborate, assume an economy consisting of n banks. Say we have a bank in∈, then a feedback loop is where an action of bank i on the system n yields, through the system, a greater than 1 impact on the bank i. For example, if a bank i falls short on its debt obligation due to exogenous events by $1 and all other banks in the system falls short endogenously, if bank i then falls short at the end by an amount greater than $1, then it means that the difference over $1 represents the endogenous default from bank icoming from bank i’s original default of $1. Hence an effect from a default loop.

Eisenberg and Noe [1] attempts to model this as is explained in the introductory section where they speak of the desire to model system of Cyclical Interdependence leading to cyclical defaults and hence feedback loops. However, the algorithm established which attempts to solve for the clearing system shows otherwise and to explain how, we begin with a sub issue.

Consider the Statement

“It is clear since there are only n-nodes, this process must terminate at n-iterations”. This is used in explaining the number of iterations it takes the fictitious default algorithm in Eisenberg and Noe [1] to clear. The set n captures the full number of banks in the economy. Now within this economy could also exist banks without any nominal obligation know as Sink Nodes. Banks such as this exists in the network because it is a pure creditor one or more banks in the system. Let us denote all non-sink nodes as N and all sink nodes as the subset S so that {} 1,,,,.nNS=…… Then the fictitious default algorithm should at most clear at N- iterations as opposed to n iterations. This is because sink nodes have no obligations and thus, amount to which they receive does not affect any other banks ability to pay.

Also, looking at the threshold where the process must terminate at N-iterations [1], it is easy to think iterations running above N-iterations, what then does this imply? The simple answer would be cyclical defaults feedback loops. To illustrate, let ei denote the exogenous cash value of a bank i, cfidenote its total assets and iπ its payment value. From gure 1, say ei = 10 and e j = 12. The payment system is denoted by the equations below;

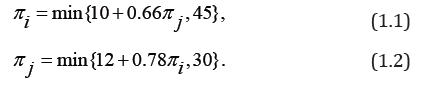
Since there are only two indebted banks, the algorithm is supposed to clear at 2-iterations. But let us take the first iteration so that π j in the bracket equals 30 and πi= 45. cfi = 30 whiles cf j = 47. Hence πi = 30 while π j = 30. Because bank i owes 45, it defaults exogenously by a total amount of 15. This is referred to as firstwave default. In the second iteration πi now updates it obligation to what it can afford which is 30 so that, π j in the bracket is still equals 30 and πi = 30. This implies cfi = 30 while cf j ≈33. Based on the new liability, the payment is now πi = 30 and πi = 30 neither defaults and thus the termination ends at 2- iterations and the payment here marks the clearing payment.

Assume the same scenario except e j = 5 so that the equation 1:2 becomes π j = min{5 + 0.78π1,30}. while all other characteristics stays the same. At the first iteration so that π j in the bracket equals 30 and πi = 45. cfi = 30 whiles cf j = 40. Hence πi = 30 while π j = 30. Because bank i owes 45, it defaults exogenously by a total amount of 15. In the second iteration πi now updates it obligation to what it can afford which is 30 so that, j in the bracket is still equals 30 and πi = 30. This implies cfi = 30 while cf j = 28:3. With the adjusted liability, bank j now defaults by a total of 1:7. We then update bank j ’s liability to 28:3 so that at the third iteration, π j in the bracket equals 28:3 and πi = 30. This means that cfi = 28:8 while cf j = 28:3. Since bank i’s adjusted liability up to this point is 30, it then defaults by 2:2 while bank j doesn’t at this stage.

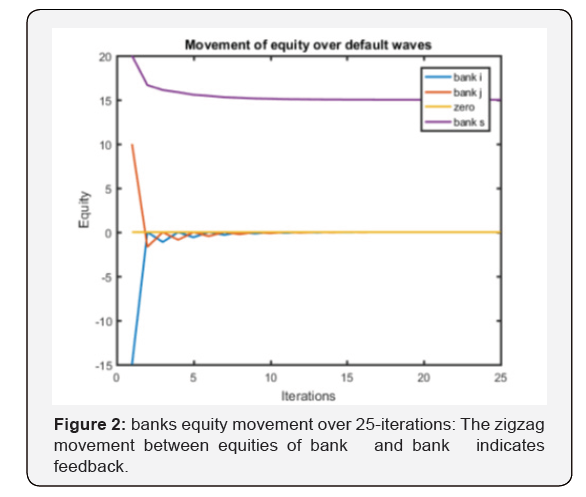
This iteration continues till each end up paying an amount approximately πi = 27:7 and π j = 26:5. Observe that in this second instance, the iterations clears at a number greater than 2. This is because if a bank i can default endogenously from its own exogenous de-fault, then the cycle has to re-account for the new default. This goes in a loop but in so far as a sink-node exists, amount of feedback decays rapidly as each loop is completed.

This is shown clearly in (Figure 2) where we see that towards 10-iterations, equity converges and thus payment is approximately determined at that point. However, the iteration runs if it can bring all defaulting banks equity to an absolute zero. This then depends on many other factors quite trivial to discuss. What is of interest is that the ability for such iterations to run much above its limit hence characterises a broken system where defaults lead to a full breakdown thus, fitting standard perception of systemic risk as opposed to default cascades/contagion.

In summary, cyclical interdependence raises possibility for systemic risk and systemic risk through networks with cyclical obligations is captured through default feedback loops. With these loops, the ctitious default algorithm runs much over the iterations equal to the number of paying rms as this time, payment is determined at the point residues from payments (equity) converges to zero.