- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Prediction of The Behavior for Polymer Blends Using Thermodynamic Model
Khalid Farhod Chasib1 and Basma Mohammed Kadhim2*
1Petroleum & Gas Engineering Department, University of Thi Qar, Iraq
2Industrial Water Department, Thi Qar, Iraq
Submission: October 14, 2019; Published : November 05, 2019
*Corresponding author: Basma Mohammed Kadhim, Industrial Water Department, Thi Qar, Iraq Recent Adv.
How to cite this article: Khalid Farhod Chasib, Basma Mohammed Kadhim. Prediction of The Behavior for Polymer Blends Using Thermodynamic Model. Recent Adv Petrochem Sci. 2018; 6(5): 555699. DOI: 10.19080/RAPSCI.2019.06.555699
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Abstract
Two polymer blends were prepared. The first one was Poly methyl methacrylate (PMMA) and Poly vinyl acetate (PVAc), and the second was Poly vinyl chloride (PVC) and Polystyrene (PS). The first blend prepared by mixing two polymers (PMMA, PVAc) with co-solvent (Chloroform) at different weight percentages (0/100, 20/80, 40/60, 50/50, 60/40,80/20,100/0). The second blend prepared by mixing two polymers (PVC, PS) with co-solvent N, N dimethylacetamide (DMAC) at different weight percentages (0/100,20/80,40/60,50/50,60/40,80/20,100/0). Two processes were used for preparation; dissolution process was used at a room temperature (25oC) and (1atm.) pressure using co-solvent. Viscosity test was performed for stock solutions (1%wt/v=1g/dL) and other concentrations (0.75, 0.6, 0.5, 0.4, 0.3 g/dL (, these concentrations are obtained by dilution of stock solution. The obtained data were collected and substituted accordance to equations (Huggins Equation) and certain criteria ( Interaction parameters ΔB , μ ) to identify the miscibility (or compatibility).To get polymer blends in solid state, The same procedure to prepare the stock solution of diluted solutions followed but the stock solutions of polymer blends were at concentration (10%wt/v) for all different compositions and then followed solvent casting ( evaporation then drying) . the solid-state samples were taken to hold tests of DSC and FTIR.
The aim of the present work was to study the thermodynamic behavior of polymer blend via determination of miscibility. Miscibility (or immiscibility) tests are performed in three techniques: viscometry method, DSC analyzer and FTIR to test polymer blend in solid state. It was found from the viscosity method that for first blend (PMMA/PVAc), the interaction parameters (ΔB, μ) are positive for all compositions therefore the system is miscible whilst the second system (PVC/PS) is immiscible where the interaction parameters (ΔB, μ) are negative. Differential scanning colarimetry (DSC) analyzer gave thermogram curves revealing one glass transition temperature for PMMA/PVAc blends except at (20/80) composition, this indicates that the system is miscible except at (20/80) composition. But, PVC/PS blends showed two glass transition temperature, so the system is immiscible. FTIR analysis for PMMA/ PVAc blends depicted a weak interaction between the two polymers and solvent due to the miscibility establishment, whilst for PVC/PS blends, there was no interaction between two polymers to establish the miscibility, this indicates immiscible system. Calculations of Flory –Huggins interaction parameter for two systems was performed and the results pointed to miscible blend for PMMA/PVAc blends and immiscible blend for PVC/PS blends. So, there is a good agreement between the experimental results and calculations of interaction parameter based on Flory – Huggins theory.
Keywords: Polymer blends Flory –Huggins interaction parameter Miscibility DSC Gas constant Hydrogen bonding Critical solution temperatures Dipole-dipole interaction Ionic interaction Resembling crystallization
Abbrevations: PVC: Poly Vinyl Chloride; PS: Polystyrene; PMMA: Poly Methyl Methacrylate; DMAC: Dimethylacetamide; DSC: Differential Scanning Calorimetry
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Introduction and Theoretical Framework
Polymeric materials find growing applications in various fields of everyday life because they offer a wide range of application relevant properties. Blending of polymers is a technological way for providing materials with full set of desired specific properties at the lowest price, e.g. a combination of strength and toughness, strength and solvent resistance, etc. Blending also benefits the manufacturer by offering improved processability, product uniformity, quick formulation changes, plant flexibility and high productivity. Polymer blends have received much attention since blending is a simple, effective approach to develop new materials exhibiting combinations of properties that cannot be obtained by individual polymers. Miscibility between two components is governed by the thermodynamics represented by the Gibbs free energy of mixing (G mix = Hmix - TSmix). The mixtures are miscible when the value of Gmix is negative, i.e., low value of Hmix and high value of S mix. Immiscibility is a rule in polymer blends because both the Hmix and the Smix are unfavorable. The Smix is unfavorable because there are few molecules of large molecular weight per unit volume. The Hmix is also unfavorable because the van der Waals dispersion force is always positive. However, when the specific interactions such as hydrogen bonding, dipole-dipole interaction, or ionic interaction are established, the miscibility between two polymer mixtures can be achieved [1].
If two polymers are mixed, the most frequent result is a system that exhibits a complete phase separation due to the repulsive interaction between the components (i.e. the chemical incompatibility between the polymers). Complete miscibility in a mixture of two polymers requires that the following condition is fulfilled:
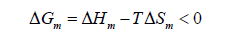
Where ΔGm, ΔHm, and ΔSm are the Gibb’s free energy, the enthalpy and entropy of mixing at temperature T, respectively. The most important characteristic of a polymer blend of two (or more) polymers is the phase behavior. Polymer blends (like low molecular weight solvents) can exhibit miscibility or phase separation and various levels of mixing in between the extremes (e.g., partial miscibility).
For a stable one-phase system, criteria for phase stability of binary mixtures of composition ∮ at fixed temperature T and pressure p are:
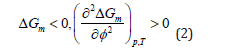
Miscible polymer blend is a polymer blend which is homogeneous down to the molecular level and associated with the negative value of the free energy of mixing and the domain size is comparable to the dimensions of the macromolecular statistical segment. The value of TΔSm is always positive since there is an increase in the entropy on mixing. Therefore, the sign of ΔGm always depends on the value of the enthalpy of mixing ΔHm. The polymer pairs mix to form a single phase only if the entropic contribution to free energy exceeds the enthalpic contribution, i.e.,
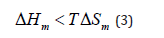
For most polymer blends the miscibility increases with increasing the pressure. The effect depends on the magnitude of the heat of mixing ΔHm. For ΔH m < 0 the miscibility is enhanced by compression, whereas for those with ΔH m > 0 it is reduced. For low molecular weight materials, increasing temperature generally leads to increasing miscibility as the TSm term increases, thus driving Gm to more negative values. For higher molecular weight components, the TSm term is small and other factors (such as non-combinatorial entropy contributions and temperature dependent Hm values) can dominate and lead to the reverse behavior, namely, decreasing miscibility with increasing temperature [2].
Consider two polymers having glass transition temperatures g T 1 and g T 2 and respective molar enthalpies H1 and H2. The molar enthalpy of a mixture of the two polymers is:
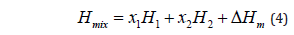
Where xi represents the mole fraction of polymer i in the blend and ⧍Hm is the excess enthalpy of mixing.
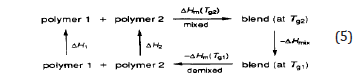
The thermodynamic cycle for the mixing process is represented by Eq 5, where H1, H2, and Hmix are the changes of enthalpies when the temperature is increased from g T l to g T 2 at constant pressure for polymer 1, polymer 2, and their blend, respectively. Hm( g T 1) and Hm( g T 2) are the excess enthalpies of mixing at g T l and g T 2. Solving Eq 5 for Hmix yields
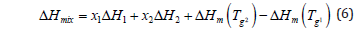
The enthalpy changes corresponding to heating the individual components and the mixture from g T 1 to g T 2 are [3]:
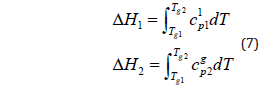
Knowledge of the glass transition temperatures ( gs T ) as function of composition reflects miscibility (or lack of it) and is decisive for virtually all properties of polymer-based materials. Immiscible polymers (not an infrequent case) clearly demonstrate two g T values for the respective pure components that are independent of composition. The glass transition temperature ( g T ) reflects the molecular rearrangement rate in supercooled liquid and thus is one of the most important factors among the many transitions and relaxations in polymers. Measurement of g T is one of the easiest determinations of whether they are miscible or immiscible in polymer mixtures. A single g T between individual two polymers appear for miscible blends whereas two Tgs are shown for immiscible blends. When g T of miscible polymer blends shows the linear relationship against the polymer composition, the value of g T is adequately expressed by the widely used Fox equation.

where w1 and w2 are the weight fractions of components 1 and 2 with g T 1 and g T 2, respectively. This equation is also used to predict the g T of copolymers.
The change in the glass transition temperature produced by blending polymer 1 and the polymer 2 can be described by equation 9 which provide a configurational entropy [3]. theory for the glass transitions of binary polymer blends. From this model, we can predict g T for the polymer blends with various compositions.
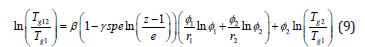
where Tg1 and Tg12 are the Tgs of the pure polymer 1 and of the blend of polymer 1 and polymer 2, respectively. ∮1 and ∮2 are the volume fractions of components 1 and 2, respectively. z is the lattice coordination number. Ὑspe is a proportionality constant representing the specific interaction such as hydrogen bonding, dipole-dipole interaction, or ionic interaction between two polymers, and ( ) 1 1 / . , u pp u pp β = zR M ΔC RM andΔC are the gas constant, the molecular [4]. weight of the repeat unit, and the isobaric specific heat of polymer 1, respectively [4].
A schematic phase diagram is shown in (Figure 1). There are three regions of different degree of miscibility:
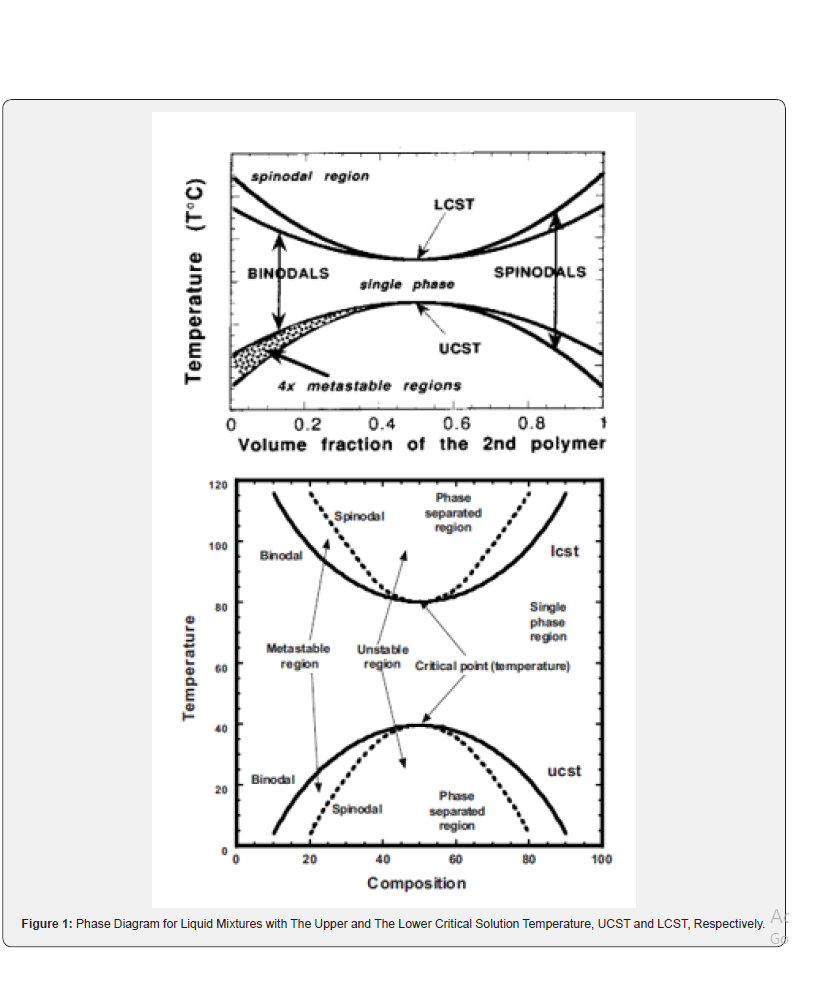
a) The single-phase miscible region between the two binodals,
b) The four fragmented metastable regions between binodals and spinodals, and
The diagram also shows two critical solution temperatures, the lower, LCST (at higher temperature), and the upper, UCST (at lower temperature). The phase diagram with two critical points is a rule for mixtures of low molar mass components, whereas the polymer blends usually show either LCST (most) or UCST [5].
The binodals (Figure 1). separate miscible (one-phase) and metastable region, the spinodals separate metastable and twophase region. The thermodynamic conditions for phase separations are given by:
A schematic phase diagram is shown in (Figure 1). There are three regions of different degree of miscibility:
A schematic phase diagram is shown in (Figure 1). There are three regions of different degree of miscibility:
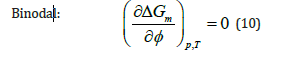
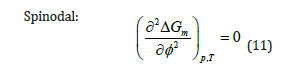
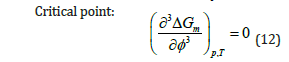
The experimental phase diagrams are often not symmetrical, unless the molecular weights of the components are similar, and in the case of large differences in molecular weights, they can be highly non-symmetric. With phase separation, the binodal defines the composition of the component 1 rich phase and component 2 rich phase (Figure 2). The tie line noting temperature T2 between the binodal points can be employed to determine the relative amounts of each phase. The tie line is illustrated in (Figure 3). The volume fraction of component 1 rich phase, ∮1r, and component 2 rich phase, ∮2r, can be determined from the expression, with ∮ representing the overall composition of the component noted in (Figure 3).
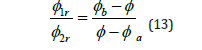
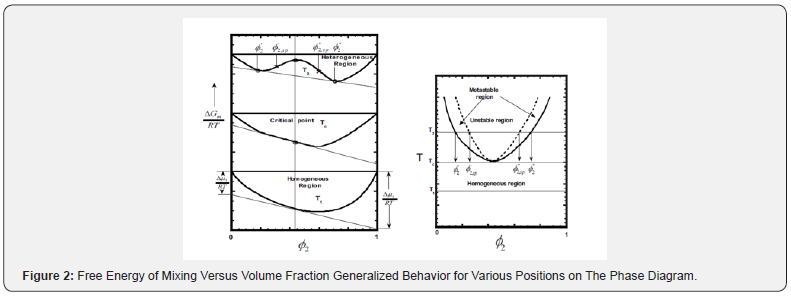
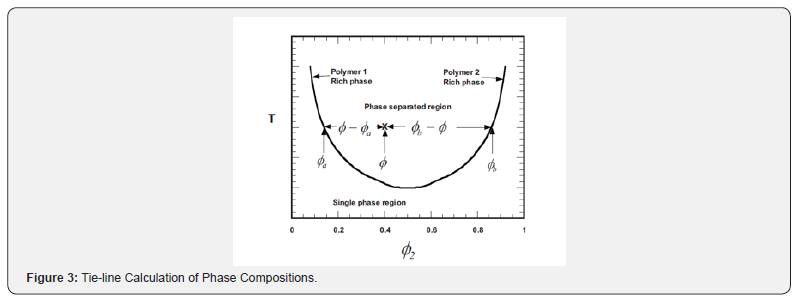
Highly miscible polymers exhibit single phase behavior over the entire temperature-volume fraction space available for experimental verification. If ucst or lcst behavior exists, it cannot be determined. At low temperatures, the ucst cannot be determined due to the glassy state restricting molecular motion (phase separation); and at higher temperatures, polymer degradation occurs before phase separation can be observed. With highly immiscible polymer blends, the phase diagram is virtually all in the twophase region with the binodal curves virtually overlapping the y axis at 0 and 1.0 volume fraction.
The phase separation takes place when a single-phase system suffers a change of either composition, temperature or pressure that forces it to enter either the metastable or the spinodal region. When the system enters from single-phase region into the metastable region, the phase separation occurs by the mechanism resembling crystallization – slow nucleation followed by growth of the phase separated domains. By contrast, when the system is forced to jump from a single-phase into the spinodal region of immiscibility the phases separate spontaneously by a mechanism called spinodal decomposition [6].
Starting point for most of the theoretical interpretations of polymer solutions and blends is the Flory-Huggins lattice theory. It is basically an extension of the concept of regular solutions on polymer solutions. Thus the model restrictions are no change of volume during mixing (incompressible model), the entropy of mixing is entirely given by the number of rearrangements during mixing (combinatorial entropy) and the enthalpy of mixing is caused by interactions of different segments after the dissolution of interactions of the same type of segments. It is a mean-field model, i.e. only average interactions are taken into consideration. The main problem was to find an expression for the entropy of mixing because it was found experimentally that polymer solutions show significant deviations from values expected for ideal solutions. Assuming a rigid cubic lattice model, this problem was independently solved for polymer solutions by Huggins & Flory [3].
The lattice theory for the enthalpy of mixing in polymer solutions, developed by Flory and Huggins, can be formally applied to polymer mixtures, which provides a rough estimation of the miscibility of the polymers. Assuming random mixing of two polymers and ΔVm = 0 yields the well-known expression for the combinatorial entropy of mixing ΔSm of the Flory-Huggins theory:
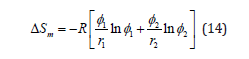
Where i is the volume fraction of the component i and ri is the number of polymer segments, R is the gas constant. It can be seen that the entropy of mixing decreases with increasing molar mass (ri is proportional to the degree of polymerization) and vanishes for infinite molar masses. Applying the concept of regular solutions and assuming all pair interactions in the framework of a mean-field theory yields for the enthalpy of mixing ΔHm:
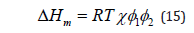
For binary systems the Flory-Huggins equation can be expressed in the following form:
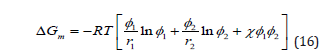
where χ is the so-called Flory-Huggins binary interaction parameter. R is the universal gas constant, and T is the absolute temperature. The first two terms of the right-hand side in Equation 16 are related to the entropy of mixing and the third term is originally assigned to the enthalpy of mixing.
For polymers having infinite molar mass (i.e. ri is infinite) the entropic contribution is very small, and the miscibility or immiscibility of the system mainly depends on the value of the enthalpy of mixing (Equation 15). Miscibility can only be achieved when χ is negative.
The term ‘parameter’ is widely used to describe χ but it is definitively better characterized by the term ‘function’, because χ depends on such quantities as temperature, concentration, pressure, molar mass, molar mass distribution and even on model parameters as the coordination number of the lattice and segment length.
For polymers, the miscibility can only be achieved when χ < cr χ . The χ parameter at the critical point cr χ can be obtained from the definition of the critical point (Figure 1) and Equation 16 as follows:
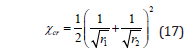
where ri is the number of polymer segments (which is proportional to the degree of polymerization).
It should be mentioned that the Equations 16 and 17 are based on the assumption that χ is not a function of composition, cr χ is only a function of the molar masses [7].
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Statement of The Problem
The factors affecting the miscibility of polymer blends will be examined experimentally and predicted thermodynamically. The miscibility and dynamics of phase separation will be investigated experimentally for different polymer blends concentrations to determine both the binodal and the spinodal curves. The relationship between the binodal curve and the phase transition, such as melting and glass transitions, will be studied to discuss the compatibility of blend system including solid component. The glass transition temperature will be experimentally determined and predicted thermodynamically to establish polymer miscibility.
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Purpose of The Study
The miscibility of the blends through glass transition temperature g T analysis by DSC will be evaluated. g T will be correlated with a measure of the intermolecular interactions, such asthe Flory-Huggins interaction parameter, χ . The effect of blend ratios on the mechanical properties and the probability [8]. to creating compatible system for the polymer blend will be studied. Methods of polymer blends preparation, and the best methods for detecting miscibility will be studied. The thermodynamic relationships will be applied to determine the free energy of mixing, heat of mixing, the binodal and spinodal curves, the critical points and thus the phase behavior [9]. Phase behavior and phase separation kinetics of polymer solutions will be investigated experimentally. The miscibility and dynamics of phase separation will be investigated in solutions of different polymer concentrations to determine both the binodal and the spinodal
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Review of The Literature
The kinetics of phase separation in “polymer + solvent” systems is of continuing interest. The phase separation in polymer solutions can be induced by changes in the temperature, the solvent (concentration or composition) or the pressure. Binder et al [8,9] studied the kinetics of spinodal decomposition of polystyrene solutions in cyclohexane induced by a temperature jump into the unstable region. Phase separation process was monitored by time- and angle-resolved light scattering at ambient pressures Berghmans et al, [10] recently carried out a numerical study of temperature-induced phase separation kinetics of polymer solutions subjected to a linear spatial temperature gradient. Their results showed that anisotropic structures and morphologies can be induced by a gradient temperature jump. In addition to temperature quench, phase separation can also be induced by exposing the solution to a nonsolvent vapor as antisolvent. Binder K [11] reported the kinetics of phase separation in a polymer solution (poly sulfone in N-methyl-2-pyrrolidinone) film induced by a nonsolvent vapor, water. The data were analyzed based on Cahn-Hilliard linear theory in the initial stages of phase separation.
Much attention has been paid to the phase behavior of polymers in compressed fluids at high pressures Guenet JM [12-14]. However, these have mostly focused on the liquid-liquid (L-L) phase boundary, with limited data on the solid-fluid (S-F) boundary. For crystallizable polymer-solvents systems, it is possible to observe the S-F boundary as well as L-L phase boundary in a phase diagram Farhod [14-17].
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Question and/ or Hypotheses
It is reasonable to believe that the changes of thermal enthalpy are caused by the occurrence of phase separation during annealing. Therefore, the phenomenon is indicative of the occurrence of phase separation Khalid FC [18-20]. The changes of thermal properties of blends composed of polymer can provide information about the occurrence of phase separation, and thermal analysis can be used to determine the phase boundary of such blends. The specific interactions such as hydrogen bonding, dipole-dipole interaction, or ionic interaction between two polymers reduce the overall entropy
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Method and Procedures
The binary blends will be made by mixing solutions (approximately 3% w/w) of each polymer in 98% formic acid. The solutions will be stirred for 2h at ambient temperature. The films for DSC and FTIR measurements will be prepared by casting the polymer solutions into shallow soda-glass dishes and allowing the solvent to evaporate slowly. The thin films will be dried at 60oC and placed under vacuum at 70-80oC for at least 3 days to constant weight. Blend compositions will be 80/20, 60/40, 50/50, 40/60 and 20/80 by weight.
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Sampling
Differential scanning calorimetry (DSC)
DSC measurements will be performed on a DuPont 910 DSC Differential Scanning Calorimeter equipped with a Thermal Analysis Data System (TA-2000). The samples will be first heated from room temperature to 250oC and maintained for 2 minutes, and then the samples will be quenched cooled to 0oC to prevent crystallization before thermograms will be taken. The scanning rate was 10oC /min. In the isothermal crystallization experiments blends samples of 9-11 mg will be used KF Chasib [21]. Starting at room temperature, the samples will be rapidly heated to melting temperature to remove any previous crystallinity. The samples will be held for 6h at a certain crystallization temperature (TC = 50, 100 and 150oC), and then will be heated to 250oC at a rate of 10oC /min under dry nitrogen atmosphere.
Fourier transform infrared spectroscopy (FTIR)
The FTIR spectra will be collected on dry thin film polymer blend samples using a UNICAM (Mattson 5000) spectrophotometer by sandwiching the film samples between two KBr disks. All of the films will be sufficiently thin to be within a range where the Beer-Lambert law is obeyed. Films will be annealed at 50, 100, and 150oC for 6h, then 32 scans will be made for each TC at a resolution of 8 cm 1.
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Instrumentation
The most common method to establish polymer miscibility is Differential Scanning Calorimetry (DSC), with which determination of the glass transition temperature ( g T ) IR spectroscopy has proved to be an excellent tool to study the hydrogen-bonding behavior in polymer blends. If the blend is immiscible, the absorption spectrum of the blend will be the sum of those for the components. If the blend is miscible because of the specific interactions, then differences will be noted in the spectrum of the blend relative to the sum of those for the components. The FTIR investigation of a miscible blend will not only reveal the presence of such an interaction, but will provide information on which groups are involved
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Data Collection and Analysis
Several approaches based on kinetic or thermodynamic features of the glass transition phenomenon will be proposed toprovide a theoretic foundation for the equations currently used to predict the compositional dependence of the g T of blends of miscible polymers Information on the experimental details and any special procedures used for preparation of the mixtures (temperature of mixing, type of solvent, drying processes, etc) can be found in the original references [1-7]. The experimental data analyzed will be obtained using conventional DSC and FTIR.
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Limitation and Delimitation
a) The most important factor leading to miscibility in low molecular weight materials is the combinatorial entropy contribution which is very large compared to high molecular weight polymers. This contribution is the reason that solvent-solvent mixtures offer a much broader range of miscibility than polymer-solvent combinations. The range of miscible combinations involving polymer-polymer mixtures is even much smaller.
b) The Flory-Huggins approach is not directly capable of predicting lcst behavior unless a temperature dependent 12 value exhibiting increasing values (negative to positive) with increasing temperature is employed.
c) The Flory-Huggins lattice model theory is an incompressible model that does not allow for the compressibility effects on the system thermodynamics.
d) For high molecular weight polymers, is negligibly small and the sign of Gm, is dominated by Hm. In general, , is negative only if there are specific associative interactions between the two polymers. Therefore, the formation of miscible polymer blends depends on the occurrence of exothermic interactions such as hydrogen bonding, dipoledipole interactions, acid-base interactions, or transition metal complexation.
e) The thermodynamic functions, entropy, enthalpy, and volume are continuous at but the first derivatives of these functions undergo discontinuities at In principle, any of these thermodynamic functions could be used to derive the relation for the compositional variation of but, in practice, the dependence of these variables on composition is not usually known. As a result, approximations of the thermodynamic functions are usually used.
f) The value of χ12 for any polymer blend is usually small and representative of the overall interaction of two different polymer molecules.
g) Many polymer pairs are not only immiscible but also incompatible, Compatibility arises from thermodynamic interaction between the blend constituents, which is a function of their physical and chemical structure
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
Significance of the Study
a) Blending of friendly environmental polymers with synthetic polymers has proven to be a suitable tool toproduce novel materials with combined characteristics in having both improved application properties and low-cost advantages in material performance.
b) Polymer blend represents very important field in processing of new materials, which has better properties in comparison with the net polymers. They are significant also from ecological and economical viewpoint..
c) The relationship between the binodal curve and the phase transitions, such as melting and glass transitions, become important to discuss the compatibility of binary blend system including solid component.
d) Considerable interest in the study of polymer blends because of their importance in academic and technical aspects. Particularly, much attention has been paid to miscibility and phase behavior in polymer blends
e) Glass transition temperature g T values are useful indeed for a variety of purposes. Particularly needed are
T values as a function of composition for binary polymer blends; they tell us whether the blends are miscible, semimiscible (called compatible) or not miscible at all.
- Review Article
- Abstract
- Introduction and Theoretical Framework
- Statement of The Problem
- Purpose of The Study
- Review of The Literature
- Question and/ or Hypotheses
- Method and Procedures
- Sampling
- Instrumentation
- Data Collection and Analysis
- Limitation and Delimitation
- Significance of the Study
- References
References
- D R Paul, S Newman (1978) Polymer Blends Vol I, II.
- O Olasbisi, L M Robeson, M Shaw (1979) Polymer-Polymer Miscibility.
- Merfeld G D, Paul D R (2000) Polymer blends: formulation. Vel1, John Wiley, sons, Inc, USA.
- Ioannis, M Kalogeras, Witold Brostow (2009) Glass Transition Temperatures in Binary Polymer Blends. Journal of Polymer Science: Part B: Polymer Physics 47(80–95).
- Szydlowski J, Rebelo L P, Van Hook W A (1992) A new apparatus for the detection of phase equilibria in polymer solvent systems by light scattering. Review of Scientific Instruments 63(2): 1717.
- Koningsveld R, Stockmayer W H (2001) Polymer phase diagrams: a textbook. Oxford University Press.
- Cahn J W (1959) Free energy of a nonuniform system II Thermodynamic basis. J Chem Phys 30: 1121.
- Binder K, Billottet C, Mirold P (1978) Theory of spinodal decomposition in solid and liquid binary-mixtures. Z Phys B 30: 183.
- Cahn J W (1965) Phase separation by spinodal decomposition in isotropic system. J Chem Phys 42: 93.
- Berghmans H, Deberdt F (1994) Phase behavior and structure formation in solutions of vinyl polymers. Phil Trans R Soc Lond A 348: 117.
- Binder K, Fratzl P (2001) Phase transformations in materials. Weinheim Wiley-VCH.
- Guenet J M (2007) Polymer-solvent molecular compounds. Amsterdam Elsevier.
- Henderson I C, Clarke N (2004) Two-Step Phase Separation in Polymer Blends. Macromolecules 37(5): 1952.
- Kirby C F, Mchugh M A (1999) Phase behavior of polymers in supercritical fluid solvents. Chem Rev 99: 565.
- Farhod Chasib K (2013) Extraction of phenolic pollutants (phenol and p-chlorophenol) from industrial wastewater. Journal of Chemical & Engineering Data 58(6): 1549-1564.
- Al Jiboury, K F C (2013) Adsorption of phenol from industrial wastewater using commercial powdered activated carbon. Journal of Selcuk University Natural and Applied Science 114-123.
- Chasib K F (2017) Extraction of Kerogen from Oil Shale using Mixed Reversible Ionic Liquids. The Eighth Jordan International Chemical Engineering Conference, p. 1,2.
- Khalid F C (2018) Experimental Measurement and Thermodynamic Modelling of Vapor-Liquid Equilibria Correlations for Prediction Azeotropic Behavior and Fitting Multicomponent Mixtures Data. Progress Petrochem Sci 1(2).
- Khalid F C (2018) Study the Vapor-Liquid Equilibrium and Excess Volume for the Binary Mixtures of Aqueous Solutions of Two Industrial Petroleum Solvents and Aromatic Hydrocarbon. Recent Adv Petrochem Sci 5(4).
- Khalid F C, Srikanth K P (2017) An Investigation on the Feasibility of Simulating the Distillation Curves and ASTM Distillation Temperature, International Journal of Oil, Gas and Coal Engineering 5(5): 80-89.
- K F Chasib (2013) Study on the effect of adding co-solvent (n-alkoxyethanol) to sulfolane on the toluene extraction, Scientia Iranica. Transaction C, Chemistry and Chemical Engineering 20: 1899-1911.






























