Review Article

Horizontal Well Economic Models Considering Reservoir Anisotrophy and Production Decline

Shedid A Shedid* and Roshdy K Shalaby

American University in Cairo (AUC), Egypt

Submission: September 10, 2019;Published: October 16, 2019

*Corresponding author: Shedid A Shedid, American University in Cairo (AUC), Cairo, Egypt

How to cite this article: Shedid A Shedid, Roshdy K Shalaby. Horizontal Well Economic Models Considering Reservoir Anisotrophy and Production Decline . Recent Adv Petrochem Sci. 2018; 6(4): 555693. DOI: 10.19080/RAPSCI.2019.06.555693

Abstract

There is a dramatic upsurge in the number of horizontal wells being drilled after they have proven to be cost effective in recovering hydrocarbon. Therefore, the determination of optimal horizontal well length with consideration of reservoir anisotropy and economic conditions is imperative for better application in anisotropic reservoirs. The purpose of this study is to develop of economic models combining reservoir properties and economic variables capable of determine the optimal horizontal drain-hole length. The newly developed models are capable of predict the optimal horizontal well length taking into consideration reservoir anisotropy, production decline model, and economic variables. These models correlate net present value (NPV) with exponential, harmonic and hyperbolic decline and are used to investigate the effects of reservoir anisotropy, oil price and discount rate on proposed horizontal well length. The results indicated that the reservoir anisotropy and production decline mode have a real impact on optimal horizontal length. Generally, the increase of reservoir anisotropic condition decreases the NPV of horizontal wells. The oil price and discount rate are also influential factors in economic feasibility of optimal length of horizontal well drilled. The application of the new economic models which consider anisotropic condition combined with economic net present value provides an effective tool(s) for making accurate decisions about application and profitability of horizontal wells. It also helps reservoir simulation studies.

Keywords: Horizontal wells Economic models Optimum wellbore length Production decline Vertical wells Reservoir system Gas flow Single-phase Well anisotropy Reservoir matrix Harmonic decline NVP Multiphase flow stimulators

Introduction and Literature Review

Horizontal wells have offered superior productivity by more penetration of the discrete compartments in complex reservoirs and providing real help in reducing water and gas coning. Field applications and research studies showed that horizontal wells offer several advantages such as; increase of contact area with the reservoir, delay coning problems of gas/water, ideal to intersect fractures for fractured reservoirs, minimize the sand production problems, maximize condensate recovery, drilling through thin reservoirs, and optimize the development of marginal oil fields [1-5]. Drilling cost of a horizontal well is much more expensive than that one of a vertical well because of required technology and equipment. Therefore, it is important to maximize the economic efficiency of horizontal wells by drilling the optimal drain-hole length. Good questions need to be answered: how an optimal horizontal length could be determined and be made economically feasible with consideration of reservoir rock properties and production decline. Reservoir engineers and geoscientists gained better understanding of lateral and vertical variations of permeability between existing vertical wells. This helped them for better planning and application of horizontal wells. The optimization process of horizontal well productivity requires consideration of spectrum of variables affecting the dynamic flow in heterogeneousand anisotropic reservoirs plus variation of pressure drop of the entire well and reservoir systems. In addition, economic analysis has to consider net present values, oil, price, discount rate…etc. [6]. developed an economic model for calculating the cost, return on investment and discounted net present value over the production life of a naturally fractured reservoir by horizontal wells.

The study did not consider the reservoir anisotropy in reservoir matrix and other reservoir/fracture characteristics [7]. categorized the previous work for horizontal wells into three types including (1) models for wells that are infinitely conductive and thus are not influenced by pressure drop in the well, (2) models where the reservoir is represented by an analytical model for single-phase flow, and (3) general models that couple multiphase flow simulators with wells. This study developed a semi-analytical well-model to quantify the effects of both single-phase oil and two-phase oil/gas flow pressure loss in the horizontal well on the overall well performance. The study did not corporate the economic effects of the involved parameters and ignored anisotropic effect [8]. indicated that horizontal well technology is costly and developed a simplified economic analysis of horizontal wells to conclude that the oil price has the greatest effect on the net present value (NPV) at a specific well length followed by productiontaxes and operating costs. The study did not answer the question about optimal horizontal well length [9].

Hu proposed two economic models correlating change of net present value with horizontal section. The first model was developed for vertical and horizontal sections of a well and the second model considered horizontal wells without vertical section, as (d NPV/L) and (d NPV/dL), respectively. This study proposed that the 3,711 ft and 4,670 ft were the optimal lengths for the two models, respectively. The proposed models [9]. were based only on cost and did not consider any reservoir properties and flow aspects. Orodu et al. [10]. developed a holistic approach for inflow and vertical lift performance and optimized the horizontal well length by considering net present value, vertical well pressure drops and diameter of drain hole. The study concluded that horizontal length of 4,000 ft is an optimal horizontal well length considering variable capital and operating costs. The study did not provide a model combing both reservoir and economic conditions. Dosunmu & Osisanya [11]. developed a simplified probabilistic economic model based on an elliptical drainage area but without consideration the effect of anisotropic condition of producing formations. This study assumed single-phase, incompressible oil, isothermal condition, and homogeneous reservoir with directional change in permeability. The study concluded that the optimal length for horizontal well was 5,000ft

Production decline curve analysis (DCA) using real production data has been used successfully for predicting well performance and life. The DCA technique is based on empirical decline models having good justifications. Three DCA models have been developed and used as (1) exponential decline (constant fractional decline), (2) harmonic decline, and (3) hyperbolic decline. Identification a representative decline model can be achieved by plotting the real production data versus time using a semi-log scale. If the plot of log (q) versus time (t) shows a straight line the decline data, follow an exponential decline model. If the plot of q versus Np shows a straight line an exponential decline model should be adopted. If the plot of log (q) versus log (t) shows a straight line, the decline data follow a harmonic decline model. If the plot of Np versus log (q) shows a straight line, the harmonic decline model should be used. If no straight line is seen in the above-listed plots, the hyperbolic decline model may be verified by plotting the relative decline rate. The objective of this study is to develop three economic models for exponential, harmonic and hyperbolic decline modes with consideration of formation anisotropy, oil price and discount rate for the determination of the optimal horizontal well length.

Development of Economic Models for Optimal Horizontal Well Length

An optimal horizontal well length should maximize the net present value (NPV) and also consider variable reservoir properties. The newly-developed models below are based on the following assumptions (1) steady-state flow of an ideal fluid, single- phase, isothermal condition, and homogeneous reservoir (2)isotropic reservoir rocks (constant directional permeability but different in horizontal and vertical directions), and (3) the pressure drop in the wellbore is very small compared to the drawdown in the reservoir, as recommended by Penmatcha et al. [7]. The total cost for drilling a horizontal well (C_w) involves cost of drilling the vertical section (C_v) and cost of drilling the horizontal section (Ch_s). The total cost can be considered to be the sum of the two costs such as; C_w, = C_v + Ch_s. Vertical well section cost (C_v) includes tangible costs such as; moving, casing/wellhead and cementing, drill bits, drilling mud and chemicals, and cased hole logging costs plus daily operating costs such as; daily rig cost, overhead, supplies, living and transportation. The cost of horizontal section (Ch_s) depends mainly on time plus all parameters required for the vertical section. In addition, drilling cost of horizontal section also includes costs for directional drilling, surveying equipment and well logging services, special rental equipment and professional supervision.

The variable cost for a single horizontal well (Ch_s) was proposed by Ruddy and Hills and given below:

Where

L= Length of the vertical well, ft

Cvf= Average footage cost of vertical drilling, $/ft

Cv= Total average cost of the vertical section, $

Cc= Cost associated for drilling the turning radius section (curve), $

Cd= Cost of daily operating rate, $/day

Chs= Cost for a single horizontal well, $

Cw= Total average cost of horizontal well, $

t= Time required to drill the horizontal interval, days

The time (t) is estimated by applying a least-square regression analysis of the straight-line relationship between the horizontal length (x-axis) and the inverse of the daily drilling progress, 1/ROP (hr./ft (y-axis). The optimization of horizontal well length requires calculation of the net-present-value (NPV), which is defined as follows:

Where

ΔN_p = incremental oil production, stb

C_o = cost per barrel of oil, $

C_w= cost of drilling and completion of the well, $

p = oil price per barrel ($40, $50, $60)

i = discount rate, %/year

n = number of years

The incremental gain of oil production from a horizontal well is given as:

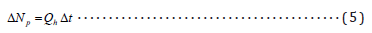
Where

Q_h= Steady State Horizontal Production Rate, stb/day

Δt = Incremental Time, Year

Substituting incremental oil production (ΔNp) from equation 5 into equation 4 yields;

The above model, equation 6, correlates the NPV and horizontal well flow rate.

Horizontal well economic model based on exponential decline

Several models have been developed to calculate horizontal well production with consideration of well anisotropy; such as Giger et al. equation (1984), which is presented below;

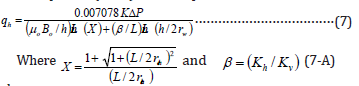
ß = anisotropic factor, μo = viscosity of the oil, cp rw = radius of the wellbore, ft, h = formation thickness, ft L = horizontal well length, ft, Kv = vertical permeability, md Bo = oil volume factor, bbl/stb, K = permeability of the formation, md

K_h = horizontal permeability, md, r_eh- = equivalent radius of horizontal well, ft

In practice, the following form of exponential decline from horizontal well is used:

Where q_i is the production rate at time (t) = 0 and b_e is an empirical constant to be determined based on production data. The decline constant (b_e) can simply be estimated as decline rate (d) for harmonic mode as described [12]. as below;

Rearranging equation 8-A provides the following form of exponential decline, which is used for calculating the incremental cumulative production (ΔNp) as expressed as below:

To convert the Np in the above, -equation, equation 8-B, to stock tank barrel (stb) it should be multiplied by 365 days.Inserting cumulative produced oil (ΔN_p) of exponential decline, equation 8-B, into the net present value equation, equation 4, yields the following equation;

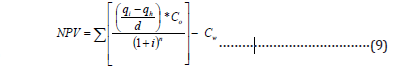
Substituting Giger’s equation for horizontal flow rate (q_h), equation 7, into the NPV equation, equation 9, results in a new economic model considering the reservoir anisotropy and other well characteristics. This horizontal well economic model is capable to predict the net present value (NPV) for exponential decline under different reservoir anisotropic conditions.

Horizontal well economic model based on harmonic decline

In practice, the same procedure of Giger equation is applied in calculating the flow rates for different lengths and different anisotropy. Also, the same economical parameters are used as for the exponential case. However, the difference comes in the equations below:

Actually, equation 10 is used for both the harmonic and hyperbolic decline models. However, they are different from each other in the value of the decline constant b. For the harmonic case, the commonly used value of constant b is equal to one (b = 1.0). Therefore, the harmonic decline equation above, equation 10, can be reduced to the form below:

Where d_i is annual decline rate of production. The cumulative produced oil for harmonic decline is given by the following equation:

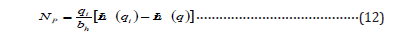
Where q_i is the horizontal well production rate at time (t) = 0, b_his a harmonic empirical constant and its value can determine as the slope of the straight line in the plot of log (q) versus log (t).

Where di is annual decline rate of production. The cumulative produced oil for harmonic decline is given by the following equation:

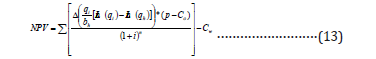
Substituting Giger’s equation for horizontal flow (q_h) into equation 13 results in the new economic model. This model correlates the reservoir anisotropy with the NPV under harmonic decline of production

Horizontal well economic model based on hyperbolic decline

The following form of hyperbolic decline, equation 10, is used for calculating the cumulative production (N_p):

As discussed, the harmonic case, that the same equation 10 is used for the two cases, however, in the hyperbolic decline constant (b) is not equal to zero or one. The following form of hyperbolic decline is used for calculating the cumulative production (N_p):

Where qi is the initial production rate at t = 0, b is an empirical constant to be determined based on production data. The hyperbolic decline constants a and b can be estimated from a plot of log (q) versus time (t).

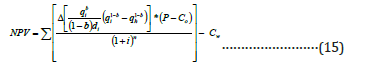
Substituting Giger equation for horizontal flow (qh) into the above-equation, equation 15, results in the new economic model. This model, equation 15, represents a new tool capable to predict the NPV as a function of reservoir anisotropic condition (K_h/K_v) under hyperbolic decline.

Result and Discussion

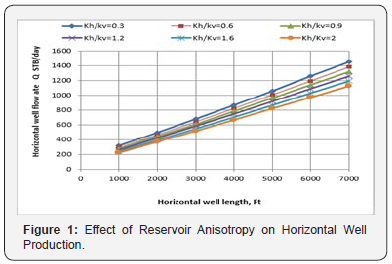
To indicate the effect of reservoir anisotropic conditions, horizontal well production rate is calculated for different rock anisotropy using Giger’s equation, as shown in Figure 1. This figure reveals an important effect of anisotropy and shows that increase of reservoir anisotropy between horizontal and vertical permeability (K_h /_v) decreases the oil production. This Figure 1 also indicates that the effect of reservoir anisotropy increases as the horizontal well length increases. The newly developed economic models consider different oil prices, discount rate, reservoir anisotropic conditions, and production decline modes of hyperbolic, harmonic and exponential. The results of these models will be used as guidance for selection of the optimal well length with the highest NPV. Table 1 lists the fluid properties used and economic constants applied. The horizontal flow rates are calculated and then those amounts of barrels are converted to revenue using three different oil prices of 40, 50 and 60$ US. Then the capital expenditure and the operating costs are deducted. The capital expenditure is represented in the cost of drilling the horizontal well, while the other costs represent the operating costs and taxes. Using the generated profit of each along the 8 years; the NPV was calculated for different oil production decline models.

Effect of reservoir anisotropy on nvp under different decline modes

The newly developed economic models are used to calculate the net present value (NPV) for different horizontal well lengths from 1,000 to 7,000ft and under different reservoir anisotropic conditions. The results are graphically presented for exponential, harmonic and hyperbolic decline modes in Figures 2a-2c. respectively. The goal of the study is to determine the optimum welllength with consideration of reservoir anisotropy for different production decline models. The above-figures 2a-2c. reveal that the optimum horizontal well length (which provides the maximum NPV) is 6,000 ft for exponential decline and 5,000 ft for other decline modes, respectively. This optimal length is determined to be 6,000ft for exponential decline and 5,000ft for harmonic and hyperbolic decline modes and under different reservoir anisotropic conditions. It is important to note that for all of the above three cases the net present value of horizontal wells decreases as the reservoir anisotropy increases.

Effect of oil price on NVP under different decline modes

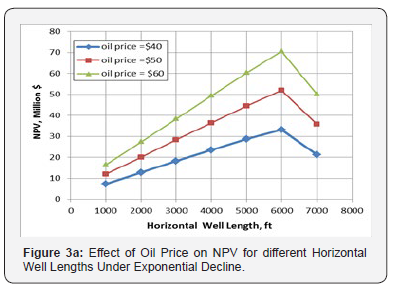
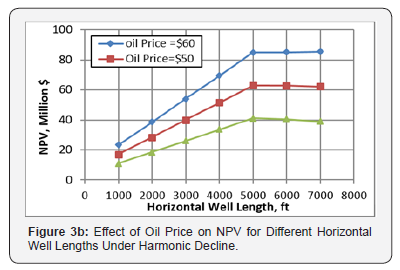
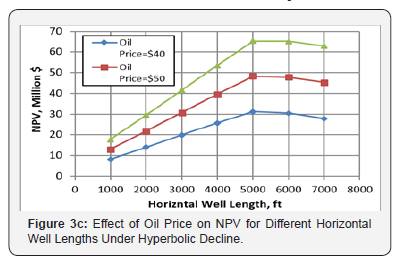
The effect of oil price on NPV of horizontal wells is investigated under different production decline modes of exponential, harmonic and hyperbolic. The attained results are depicted in figures 3a-3c. below. Figure 3a reveals that the increase of oil price increases the profitability of horizontal wells and the optimum length providing the maximum NPV is at 6,000ft for exponential decline model of production. Figures 3b & 3c indicate that the optimum well length is at 5,000 ft for both harmonic and hyperbolic decline models for different oil prices. The three figures above, figures 3a-3c. indicate that the maximum NPV of horizontal wells depends on the production decline model. Therefore, determination of the optimum horizontal well length has to consider the production decline mode of the reservoir under development.

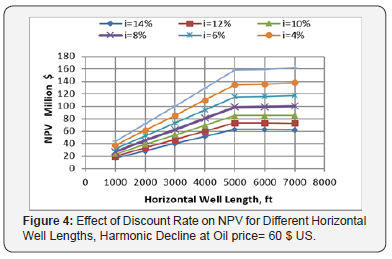
Effect of discount rate on selected horizontal well length

Discount rate is an important economic parameter affecting applications of horizontal wells. The harmonic decline model and an oil price of 60$ US are used to study the effect of different discount rate on the NPV of horizontal wells. The calculated results are presented in figure 4 below. The increase of discount rate decreases the NPV of horizontal wells, as depicted in figure 4. At constant proportions figure 4 also indicates that the optimal horizontal length is at 5,000ft and it is independent on the discount rate.

Comparison of different production decline models

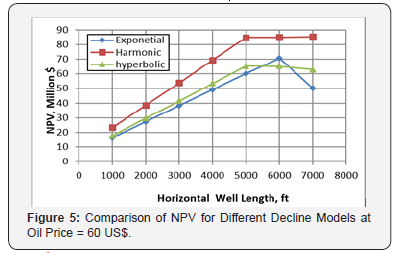
An oil price of 60$ US is used with constant discount rate and reservoir properties to compare the results of exponential, harmonic and hyperbolic decline models. The results of the calculated NPV are graphically presented versus horizontal well length in figure 5 below. at oil price = 60$ US. Figure 5 reveals that the maximum NPV for horizontal wells depends upon the production decline model representing the reservoir. It can be concluded that both harmonic and hyperbolic models calculate the optimum well length to be 5,000ft while the exponential models provide another optimum horizontal length of 6,000ft.

Conclusion

Determination of optimal horizontal well length requires consideration of reservoir anisotropy and economic variables for a feasibly economic hydrocarbon recovery. The following pertinent conclusions of this study are summarized below:

a) Reservoir anisotropy has a paramount effect on the production of horizontal wells. In general, the increase of reservoir anisotropy (K_h/K_v) decreases the oil production and its effect increases as the horizontal well length increases.

b) New economic models have been developed for horizontal wells. These models correlate the reservoir behavior of anisotropy and production decline mode with the economic variables of oil price and discount rate.

c) The optimal drain-hole length of horizontal wells depends upon the production decline model representing the reservoir. This optimal length has been determined to be 5,000ft for harmonic and hyperbolic decline models and 6,000 ft for the exponential one.

d) The increase of oil price increases the profitability of horizontal wells while the increase of discount rate decreases it.

Acknowledgement

This work is conducted as a part of a funded research project supported by the American University in Cairo (AUC) under the contract agreement # SE-PENG-FY 17-RG (2)-2016. The authors would like to express their grateful appreciation to the AUC management for funding this project and encouragement for publication.

References

1. Giger FM, Reiss LH, AP (1984) The Reservoir Engineering Aspects of Horizontal Drilling. SPE paper 13024-MS, SPE Annual Technical Conference and Exhibition, Houston, Texas, USA.
2. Shedid A E, Osisanya S, Tiab J (1996) A Simple Productivity Equation for Horizontal Wells Based on Drainage Area Concept. SPE Paper- 35713, the SPE Western Regional Meeting, Anchorage Alaska.
3. Joshi S D (1998) Augmentation of well productivity with slant and horizontal wells. Journal of Petroleum Technology 40(6): 729-739.
4. Shedid SA, Zikri AY (2001) Sensitivity Analysis of Horizontal Well Productivity under Steady-State Conditions. Paper SPE-72121-MS, the SPE Asia Pacific Improved Oil Recovery Conference, Kuala Lumpur, Malaysia.
5. Birchenko VM, Usnich AV, Davies DR (2010) Impact of frictional pressure losses along the completion on well performance. Journal of Petroleum Science and Engineering, 73(3-4): 204-213.
6. Guo G, Evans R D (1993) An Economic Model for Assessing the Feasibility of Exploiting Naturally Fractured Reservoirs by Horizontal Well Technology. Paper SPE 26676-MS, the SPE Annual Technical Conference and Exhibition, Houston, Texas.
7. Penmatcha VR, Arbabi S, Aziz K (1997) Effects of pressure drop in horizontal wells and optimum well length. Paper SPE 37494-MS, SPE Production Operations Symposium, Oklahoma City, Oklahoma.
8. Osisanya SO (1997) Economic Analysis of Horizontal Wells. Paper SPE 37495-MS, the SPE Production Operations Symposium, Oklahoma City, Oklahoma.
9. Hu Y (2011) Study on the Design of Optimal Horizontal Section Length of Horizontal Wells. ijbss 2(1).
10. Orodu O D, Fadiaro, AA, Enebeli EE (2012) Realistic Optimization of Well Length for Horizontal Drilling. Brazilian Journal of Petroleum and Gas. 6(2): 53-65.
11. Dosunmu I, Osisanya S (2015) An Economic Approach to Horizontal Well Length Optimization. SPE-177866-MS, Abu Dhabi International Petroleum Exhibition and Conference, UAE.
12. Guo B, Lyons W, Galambos A (2007) Petroleum Production Engineering, A Computer- Assisted Approach. Elsevier Science & Technology Books (1^st edt).