petrochemical science journal | Juniper Publishers

Quantum-Chemical Modeling of the Non-Linear Graphenes from 7, 9,10 Hexagons in the Framework of the Molecular ModelMethod of Mndo

Babkin VA¹*, Andreev DS², Ignatov AV¹, Bakholdin II¹, Titova ES³, Rakhimov AI³, Rakhimova NA³, Fedunov RG⁴, Lebedev NG⁴ and Zaikov GE¹

¹Department of Chemical Sciences, Volgograd State Technical University, Russia

²Department Mathematical and Natural Sciences, Volgograd State Technical University, Russia

³Department of Organic Chemistry, Volgograd State of Technical University, Russia

⁴Department of Theoretical physics and wave processes, Volgograd State of Technical University, Russia

Submission: July 01, 2017; Published: September 25, 2017

*Corresponding author: Babkin VA, Department of Chemical Sciences, Volgograd State Technical University, Russia, Email: Babkin_v.a@mail.ru

How to cite this article: Babkin VA, Andreev DS, Ignatov AV, Bakholdin II, Titova ES3, et al . Quantum-Chemical Modeling of the Non-Linear Graphenes from 7, 9, 10 Hexagons in the Framework of the Molecular ModelMethod of Mndo. Recent Adv Petrochem Sci. 2017;3(3): 555611. DOI:10.19080/RAPSCI.2017.03.555611

Abstract

The quantum-chemical calculation of the non-linear graphene molecules from 7, 9 and 10 hexagons by the MNDO method with optimization of geometry for all parameters by the standard gradient method within the framework of the molecular nonlinear graphene model was performed for the first time. The optimized geometric and electronic structure of these compounds is obtained. The acid strength (pKa = 33) of the studied graphenes is theoretically estimated. The molecules of 7, 9 and 10 hexagons belong to the class of very weak acids (pKa> 14). It is shown that an increase in the number of hexagons reduces the Harte energy of the studied graphenes.

Keywords: Quantum-chemical calculation; MNDO method; Grapheme molecules of 7, 9 and 10 hexagons; Acid strength

Introduction

Quantum-chemical calculations of the nonlinear graphenes from 5-6 hexagons within the framework of the molecular model by the MNDO method for the first time were performed with optimization of geometry for all parameters in [1]. In order to obtain new regularities and, in particular, the energies of the highest occupied molecular orbital energy (E_HOMO), the energy of the lowest unoccupied molecular orbital energy (E_LUMO) of the studied graphenes, depending on the hexagons under research, it is reasonable to continue these calculations for 7-10 and so on hexagons, which will allow us to estimate their electronic conductivity. In connection with this, the goal of the present paper is the quantum-chemical calculation of the nonlinear graphenes from 7-10 hexagons within the framework of the molecular model.

Methodical Part

The MNDO method, which reproduces the energy characteristics of molecules fairly well [2], was chosen for the quantum-chemical calculation of the non-linear graphenes from 7, 9 and 10 hexagons (it is impossible to build a model from 8 hexagons that is adequate to graphene) within the framework of the molecular graphene model.

Optimization of the geometry of the models was carried out in all parameters by the standard gradient method built into Firefly [3], which is partly based on the GAMESS source code [4], in the approximation of the isolated molecules in the gas phase. The acid strength of the studied molecules was estimated using the formula pKa = 42.11 - 147.18qmax^H+ [5] (where qmax^H+ is the maximum charge on the hydrogen atom, pKa is the universal acidity index). The program MacMolPlt [6] was used to visualize the model of the molecules. These graphenes are shown schematically in Figure1.

Results of Calculations

The optimized geometric and electronic structure, total energy (E0) and electron energy (E_EL), the highest occupied molecular orbital energy (E_HOMO), the lowest unoccupied molecular orbital energy (E_LUMO) and the Harte energy (EH) as a criterion for the electronic conductivity of the molecules of the researched graphenes, obtained by the MNDO method, are shown in Figure 1-4 and Table 1-4. Using the formula pKa = 42.11 - 147.18 qmax^H+ [5] (qmax^H+ = +0.06 - the maximum charge on the hydrogen atom, the same for all three models pKa is the universal acidity index, see Table 1-3, we find the value of the acid force pKa, Equal to 33. In addition, Table 4 shows, that the addition of three hexogons to the polycyclic hydrocarbon reduces the Hartree energy from 681 kJ/mol to 583 kJ/mol ,or from 7.1 eV to 6 eV [7].

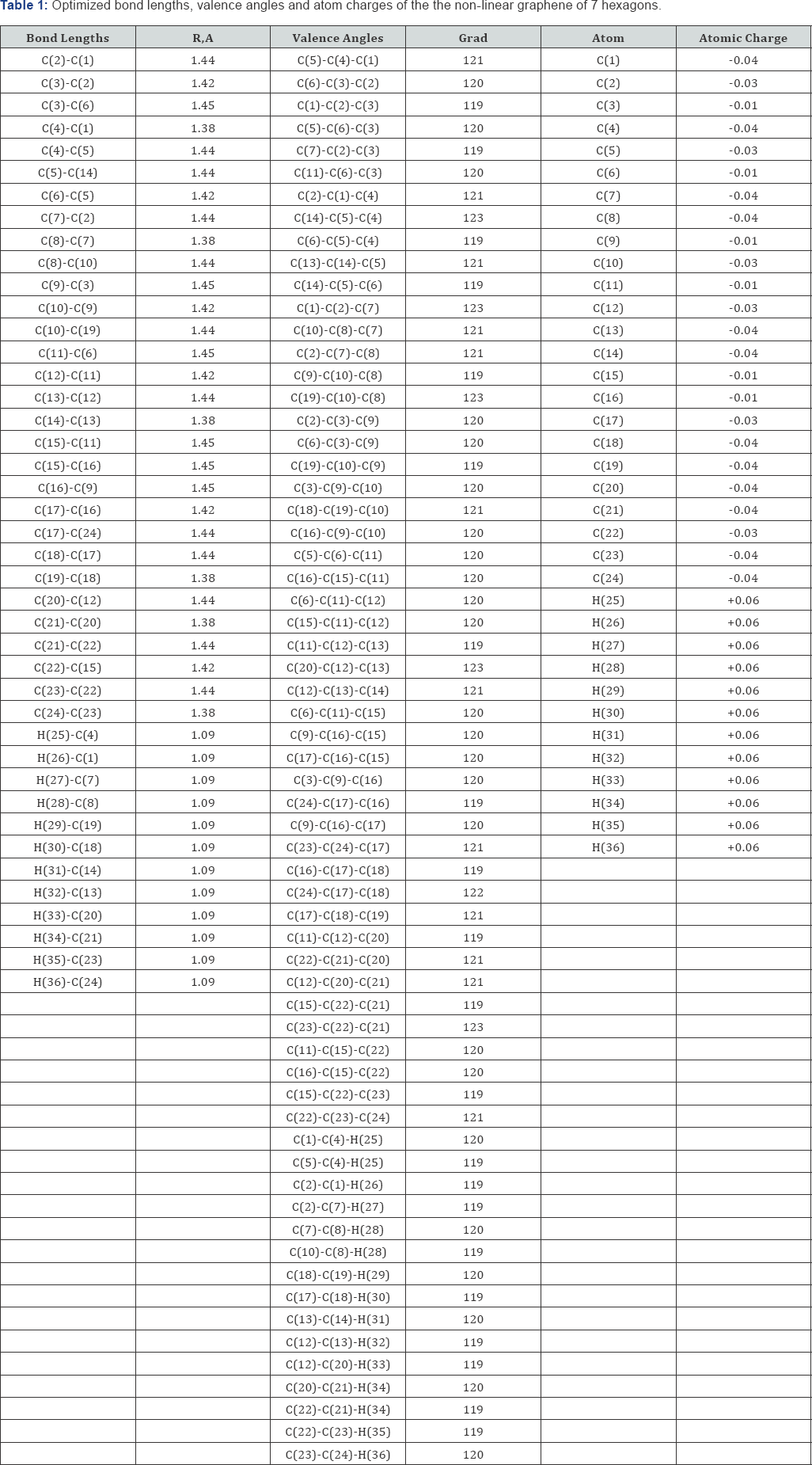
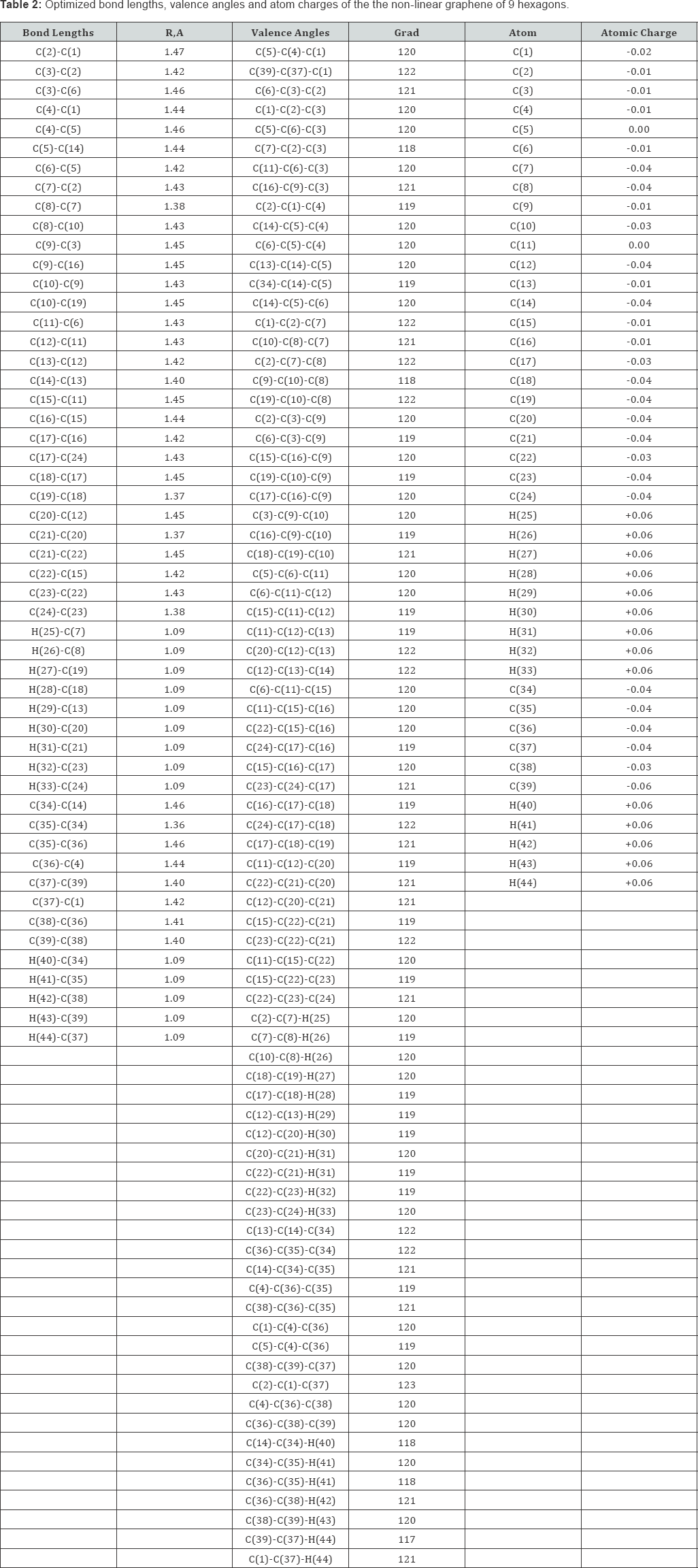
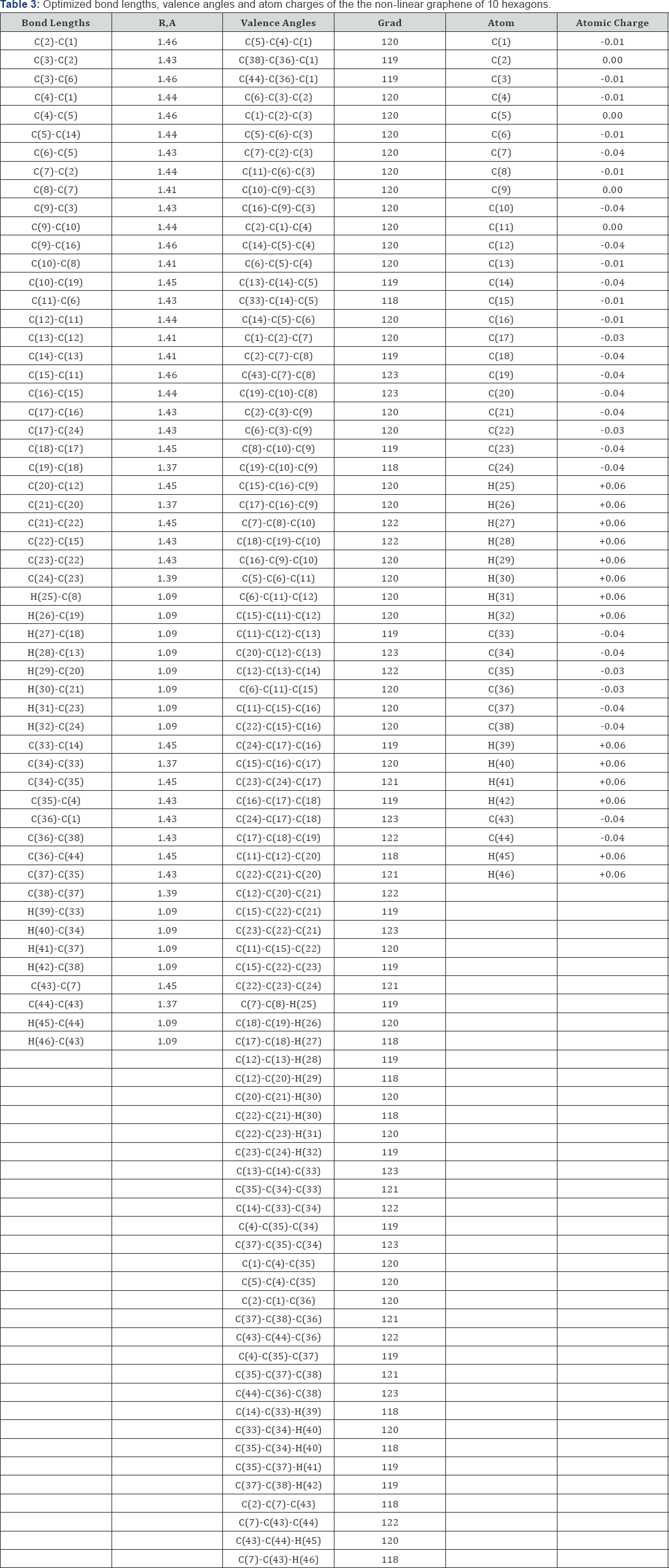
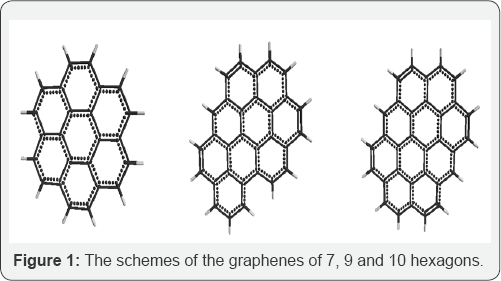
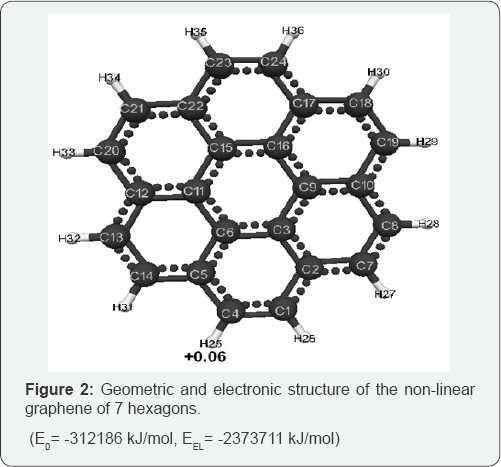
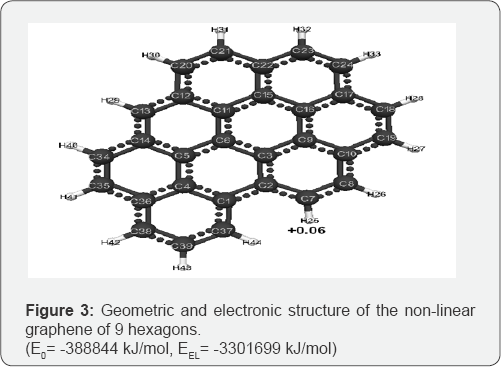
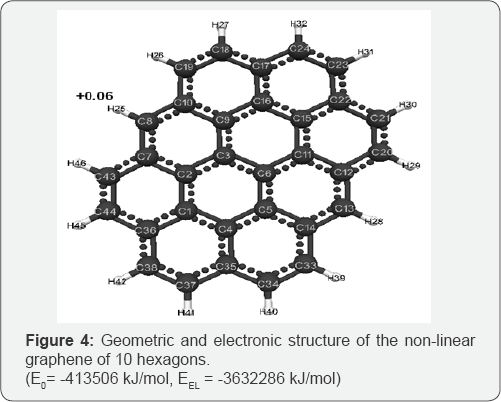
Conclusion

Thus, we performed the quantum-chemical calculation of molecules of non-linear graphenes consisting of 7, 9 and 10 hexagons by the MNDO method for the first time. Their optimized geometric and electronic structure is obtained. The acid strength of these graphenes is theoretically estimated: pKa = 33. It is established that the molecules of 7, 9 and 10 hexagons belong to the class of very weak acids (pKa>14). An increase in the number of hexagons in nonlinear graphenes reduces the Hartree energy, which coincides with the trend noted in [1].