Wu Jianwei; Wei Hai; Lao Zhenhai; Liang Guobao; Lin Bo

doi:10.19080/RAEJ.2025.06.555682

Graphical Matching Design for Suspension Systems Considering Multiple Conditions and Indexes in the Time-Frequency Domain

Wu Jianwei, Wei Hai, Lao Zhenhai, Liang Guobao and Lin Bo*

Institute of new Technology, Guangxi Liugong Machinery Co., Ltd., Liuzhou 545007, China

Submission:December 16, 2024;Published:January 08, 2025

*Corresponding author:Lin Bo, Institute of new Technology, Guangxi Liugong Machinery Co., Ltd., Liuzhou 545007, China Email Address: linbo@liugong.com

How to cite this article: Wu J, Wei Hai, Lao Z, Liang G, Lin B. Graphical Matching Design for Suspension Systems Considering Multiple Conditions and Indexes in the Time-Frequency Domain. Robot Autom Eng J. 2025; 6(3): 555682.DOI: 10.19080/RAEJ.2025.06.555682

Abstract

In the vehicle suspension systems and dynamics, suspension parameters play a crucial role in determining ride comfort and handling stability. The effectiveness of suspension matching requires a comprehensive analysis of multiple performance indexes across various operating conditions. For suspension designs with significant load variations between empty and full loads, it is essential to develop a balanced design process that accounts for sprung mass vibration, suspension travel, suspension frequency, road conditions, driving speed, and tire dynamic load. Such a comprehensive approach is necessary to meet all performance indexes and minimize the extensive parameter tuning and experimental validation typically needed beyond traditional frequency-domain selection methods. This paper addresses these challenges by developing a multi-condition Simulink parametric simulation model specifically for suspension systems with substantial load variation. The model incorporates diverse road conditions and driving speeds and defines multiple performance indicators for suspension matching. Furthermore, it integrates an iterative process that transitions from frequency-domain preliminary selection to time-domain optimized adjustment. This approach results in a generalized, graphical methodology for suspension system matching. Building on this foundation, the paper presents a detailed matching process along with case studies to illustrate the application of the proposed methodology. This work provides a systematic framework and selection basis for the design and optimization of vehicle suspension systems, offering valuable guidance for achieving optimal suspension performance.

Keywords: Suspension system; Parameter matching; Empty and full loads; Damping coefficients for tension and compression; Graphical matching design

Introduction

In the realm of vehicle dynamics and suspension systems engineering, the suspension system, composed of tires, springs, dampers, and linkages, serves as the pivotal interface mediating the vehicle’s interaction with the road. Its design is critical, profoundly affecting ride comfort, handling, road possibility, and fatigue durability, thereby making it an indispensable component of vehicular systems [1-2]. Crafting a robust suspension design necessitates a meticulous balance among several factors, including dynamic vehicle response, road surface irregularities, vehicle load variations, driving speed fluctuations, tire dynamic loads, and suspension travel requirements. The task presents itself as a complex multi-objective optimization challenge, where enhancing ride comfort may compromise handling, and vice versa. Thus, achieving an equilibrium among these diverse conditions and performance indexes remains a considerable challenge in suspension design.

With the evolution of computational technologies and simulation methodologies, Computer-Aided Design (CAD) and vehicle dynamics modeling have advanced significantly. These innovations allow for the exploration of nonlinear suspension characteristics across varied road conditions, speeds, and parameters, facilitating comprehensive performance evaluations during the design phase. This technological leverage not only boosts design efficiency but also enhances performance compatibility [3]. For instance, David Mantilla et al. [4] employed a parameter-driven ANSYS APDL with multibody dynamics to ascertain optimal suspension stiffness and damping under various loads. Lu et al. [5] developed a multibody dynamics model for a leaf-spring suspension system, optimizing ride comfort through time-domain road profile reconstruction, and derived ideal suspension parameters. Chen et al. [6] proposed a modeling method integrating nonlinear mathematical models with traditional vibration models, utilizing a coupling of nonlinear dynamics and hierarchical optimization to improve suspension accuracy and effectiveness. Shen et al. [7] introduced an innovative Inerter-Spring-Damper (ISD) suspension structure, integrating an inerter with a conventional dynamic damper, with simulations confirming its enhanced performance. Zhao et al. [8] optimized front suspension parameters for large mining dump trucks, exploring the vehicle’s handling and ride comfort. Xiong Ke et al. [9] devised a nine-degree-of-freedom model for heavy-duty vehicles to optimize ride comfort, identifying optimal stiffness and damping parameters. Pazooki et al. [10] proposed the use of nonlinear dampers designed with the Energy Balance Method (EBM), further elevating vehicle ride performance. Fernandes et al. [11] demonstrated that asymmetric damping and geometric nonlinearity in suspension models improve ride comfort. Song Yong et al. [12] introduced a bionic suspension structure to enhance the ride smoothness of commercial vehicles with significant changes in sprung mass.

Research has spawned numerous computer-simulated suspension design methods, innovative suspension architecture propositions, and explorations into nonlinear stiffness and damping. Nonetheless, many methodologies sidestep the vehicle’s design integration phase, zeroing in on performance optimization tasks such as developing multibody dynamic models. Traditional frequency-domain approaches can be overly simplistic, neglecting the nuanced matching process for different tensile and compressive damping coefficients. As a result, current suspension parameter matching during the design phase frequently depends on engineer experience and later-stage test calibrations based on empirical frequency-domain methodologies [13-15]. Despite these advances, empirical determinations often govern suspension design, particularly regarding the ratio of tension-compression damping. These values, although effective, lack a standardized comprehensive performance evaluation metric. Particularly in cases with marked load differences, a harmonized design process considering suspension travel, frequency, road conditions, speed, and tire dynamics is indispensable. Without such a process, fulfilling all suspension performance indexes proves daunting, often requiring extensive experimental validation. In mismatched parameters for suspension systems, subsequent improvements and adjustments demand considerable labor and costs.

To address these challenges, this paper proposes a parameterized Simulink simulation model tailored for suspension systems with significant load variations. The model considers various driving conditions and speeds and defines comprehensive suspension performance indexes. By adopting a systematic iterative process transitioning from empirical frequency-domain selections to time-domain optimizations for the parameter matching, we formulate a generalized, graphical methodology for suspension design matching. The efficacy of this approach with a detailed matching process and case study are illustrated for elucidating the variation patterns of suspension parameters, thereby providing a foundational selection framework for vehicle suspension design.

Suspension system

Quarter vehicle model

(Figure 1) shows a quarter vehicle model [16]. Considering the quarter vehicle model with different damping coefficients, the dynamic equations can be expressed as

where m_u and m_s denote the unsprung mass and sprung mass, respectively. z_r,z_u and z_s are the vertical displacement of road surface, unsprung mass, and sprung mass, respectively. kt and ct are the stiffness and damping of tire, respectively. c_sc and c_st represent the compression damping coefficient and tensile damping coefficient of the suspension, respectively. k_s represents the stiffness of the suspension, and sign (·) is a symbolic function.

When the damping coefficients of tension and compression are equal (i.e. c_s=c_st=c_sc), the frequency domain analysis can be used, which can be linearized into the following dynamic equation

According to the complex modal theory of mechanical vibration systems [17], the natural frequency and damping ratio of a quarter of the vehicle model can be obtained. Here are a few common terms for linear suspension systems:
• The partial frequency of the suspension refers to the natural frequency of a single-degree-of-freedom vibrational system when the unsprung mass is fixed. It can be calculated as

• The partial damping ratio of the suspension refers to the damping ratio of a single-degree-of-freedom vibrational system when the unsprung mass is fixed. It can be calculated as

• The suspension frequency and damping ratio refer to the counterpart concerning the natural frequency and damping ratio of the sprung mass, as calculated using the complex modal theory in equation (3).

Random road surface model

The nonlinear differential equations (1) and (2) typically use filtered white noise to construct random road surface excitations, with the following formulas [18-19]

where G_q(n₀) is pavement unevenness coefficient, and the value of that of Chinese national standard C-grade pavement is 256×10^-6 m³. f₀ is the lower cut-off frequency and f₀ = 0.0628 Hz. V is the velocity of vehicle with unit m/s. w(t) is white Gaussian noise with power spectrum 1. n₀ is the frequency index, and n₀ = 0.1 m^-1.

By changing the driving speed and road level, random excitation inputs for different road surfaces can be obtained. To evaluate the comprehensive performance of various road suspension systems, common grades of road surfaces can be combined. (Figure 2) shows the simulated roughness curves of A-grade, B-grade, C-grade, and D-grade hybrid road surfaces at a vehicle speed of V=35 km/h, where 0~30 s, 30-60 s, 60-90 s, and 90-120 s are A-level road surface, B-class road surface, C-grade road surface, and D-grade road surface, respectively.

Parametric simulation model with multi-conditions

(Figure 3) shows the parametric simulation model with multi-conditions based on Simulink. This model consists of four modules: road surface module, dynamics module, display module, and performance index module. Among them, the road surface module contains five pavement models, namely random road, single pulse pavement, sine pavement, continuous pulse pavement, hybrid random and pulse road, and hybrid random road. Dynamics model of the suspension can be constructed by (Equations 1-2).

Performance evaluation indexes

Usually, the main performance indexes for evaluating suspension systems include sprung mass acceleration, tire dynamic load and suspension dynamic stroke [16]. However, for vehicle systems with significant changes in empty and full loads, the suspension stroke varies greatly. To meet the comprehensive requirements of maneuverability and comfort, shock absorbers with different damping coefficients for tension and compression are usually designed, which makes these traditional indexes unable to meet the practical design requirements. In response to this, the performance indexes of the maximum and minimum deformations are added, and the traditional indexes under empty and full loads are distinguished.

Sprung mass acceleration

When significant variations between empty and fully loads exist in the vehicle system, sprung acceleration is divided into unloaded sprung mass acceleration and fully loaded sprung acceleration. They are denoted by a_sE and a_sF, respectively. For random road surfaces, the performance indexes are primarily evaluated using the Root Mean Square (RMS) value, defined as Index1 and Index2:

where a_sE(t) and a_sF (t) denote the accelerations of the unsprung mass under the empty and full loads, respectively. The smaller the RMS value of the sprung mass acceleration, the less vibration is transmitted to the vehicle body.

Tire dynamic load coefficient

Tire dynamic load coefficient denotes the ratio of the tire dynamic load to the static load. For random road surfaces, it is evaluated using its RMS value to assess the suspension’s ground performance. In practice, the tire dynamic load coefficient is often higher for unloaded conditions than for fully loaded conditions. The tire dynamic load coefficient under the empty load is thus defined as Index3:

where z_uE(t) and Δ_t denote the displacement of the unsprung mass and the static deformation of the tire under the empty load, respectively. When the tire load coefficient exceeds 1, the tire will lose contact with the ground. Hence, a smaller index is preferable, indicating lower tire dynamic load and less road damage.

Minimum and maximum suspension deformations

Considering the static equilibrium position, the relative displacement between the sprung and unsprung masses represents the absolute deformation of the suspension. The maximum relative displacement indicates the minimum suspension deformation, which typically occurs under unloaded conditions; the minimum relative displacement indicates maximum suspension deformation, usually occurring under fully loaded conditions. Therefore, the minimum and maximum deformations can be expressed as

where z_sE(t) and z_sE(t) represent the displacements of the sprung mass under the empty and full loads, z_uF(t) denote the displacements of the unsprung mass under full load, and e Δ and f Δ represent the static deformations of the suspension under the empty and full loads, respectively.

It can be seen that if the minimum deformation is greater than 0, the suspension experiences an extension effect, losing its support function. Similarly, if the maximum suspension deformation exceeds the allowable structural limit, the stop block will be impacted in the suspension system, severely affecting ride comfort and durability. Therefore, Index4 needs to be less than 0, and Index5 needs to be greater than the negative maximum suspension deformation. (Figure 4) shows the deformation curves of a vehicle suspension system with suspension stiffness.

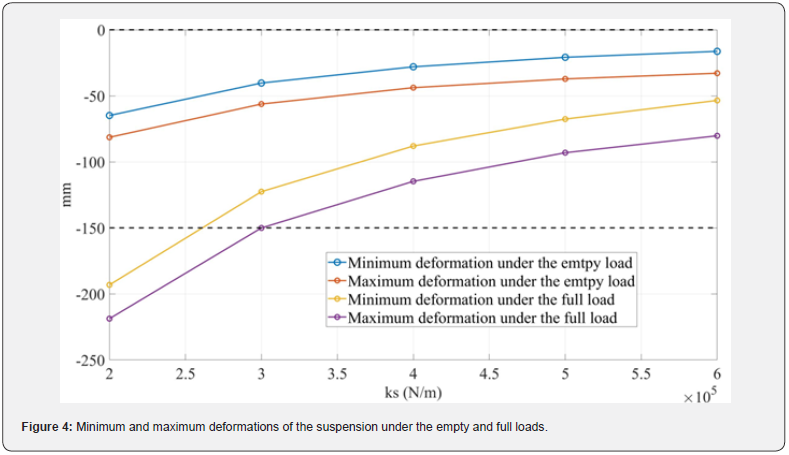
Suspension workspace

Suspension workspace refers to the displacement between the sprung and unsprung masses, disregarding the static equilibrium position of the suspension. For random road surfaces, the performance is primarily evaluated using the RMS value, represented by Index6 and Index7:

Design process of matching suspension

The optimal matching design of a suspension system is crucial for vehicle dynamics. Its objective is to obtain the minimum sprung mass acceleration under the requirements of suspension travel and tire dynamic load, when vehicles with various speeds diver on different road surfaces. The three most important parameters characterizing suspension performance are suspension stiffness, tension damping coefficient, and compression damping coefficient.

Initial selection of stiffness and damping

For truck front suspensions, the desired frequency under full load is generally between 1.5 and 2.1 Hz, while for rear suspensions, it is between 1.7 and 2.17 Hz; the damping ratio requirement is between 0.1748 and 0.4136, which lies within the range for optimal comfort and safety [20-21].

Considering the sprung mass m_sF under the full load, the initially selected stiffness and selected damping coefficient can be expressed as

where f and ζ are the partial frequency and damping ratio for the suspension system, respectively.

For vehicles with significant variation between empty and full load, an empirical value of 1.8 Hz and 0.4136 is used as the initial selection for fully loaded suspension frequency and damping ratio.

Optimization of the stiffness

Based on the initial stiffness selection, the parametric Simulink model of mixed road surfaces is used to analyze the variation patterns of different indexes under various stiffness conditions, optimizing for the best overall performance result. The obtained optimal stiffness is denoted as k_opt . The set of stiffness variation coefficients is defined as

Optimization of the damping coefficient

Based on the optimal stiffness k_opt,the parametric Simulink model of mixed road surfaces is used to analyze the variation patterns of different indexes under various damping coefficients, optimizing for the best overall performance result, denoted as c_opt. The values of the damping variation coefficients are defined as

Optimization of the ratio of tension-compression damping

Based on the optimal stiffness k_opt, and damping c_opt, the parametric Simulink model of mixed road surfaces is used to analyze the variation patterns of indexes concerning the tensioncompression ratio. By combining graphical curve results, the optimal ratio achieving the best comprehensive performance is obtained, denoted as r_opt. The values of the tension-compression damping ratio coefficients are defined as

Design case of matching suspension

Suspension system dynamics parameters

With reference to similar vehicle products and according to the tire testing parameters provided by the supplier, the suspension system dynamics parameters and design requirements shown in are given in (Table 1). The purpose of suspension matching is to obtain the optimal suspension stiffness and tension-compression damping coefficients under the requirements of suspension space, tire dynamic load and sprung mass acceleration.

Initial selection of stiffness and damping

According to the design process of matching suspension in section 3, the initial stiffness and damping coefficient can be obtained as follows: k=537 N/mm, c= 39.3N·s/mm.

Optimization of the stiffness

The initial stiffness value is multiplied by an element of the set given in Equation (16), yielding various curves of suspension performance indexes as stiffness varies by using the parametric Simulink model of mixed road surfaces, as shown in (Figure 5). Specifically, Figure 5 (a-e) and (g-h) display the curves of these indexes as stiffness changes, while Figure 5 (f) and (i) show the variations in suspension frequency and damping ratio with respect to stiffness.

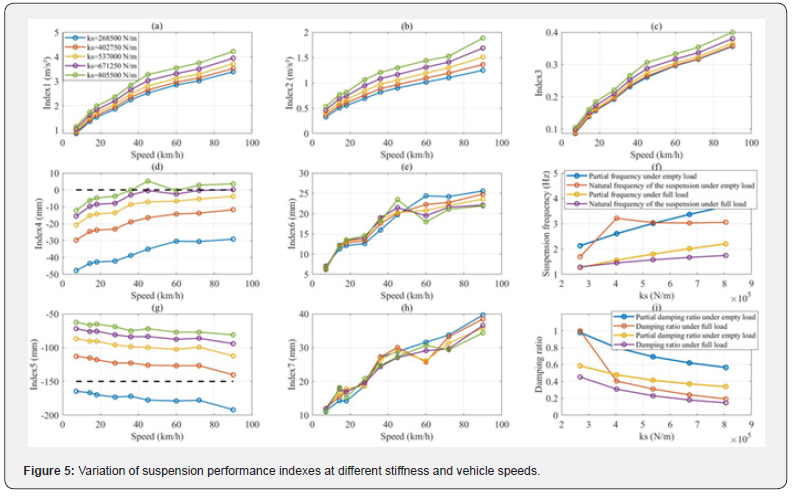
In (Figure 5), Index1 and Index2 are the RMS values of unsprung mass acceleration under the empty and full loads, respectively; Index3 is the tire dynamic load coefficient under the empty load; Index4 and Index5 are the minimum and maximum suspension deformations, respectively; Index6 and Index7 are the RMS values of Suspension workspace under the empty and full loads, respectively.

According to (Figure 5), it can be observed that:
1. Index1, Index2 and Index3 increase with increasing stiffness, as shown in Figure 5 (a-c). Therefore, for these indexes, a lower suspension stiffness is favorable.
2. Index6 and Index7 decrease with increasing stiffness, as shown in Figure 5 (e) and (h). It indicates that for these two indexes, higher suspension stiffness is beneficial.
3. Considering the suspension travel design requirements, the minimum deformation of the suspension should exceed -150 mm, and the maximum deformation of suspension should be less than 0. According to Figure 5 (d) and (g), the permissible stiffness range can be approximately determined as greater than 380 and less than 660 N/mm.

To obtain the minimum Index1, Index2 and Index3, k_s=400 N/mm is a better choice under the requirements of suspension travel design and dynamic deformation. It is determined from Figure 5 (f) and (i) that the partial frequencies of the suspension system under the empty and full loads are about 2.61 and 1.56 Hz, respectively; the partial damping ratio is approximately 0.478 and 0.799, respectively.

It is noted that the minimum and maximum deformations of the suspension at maximum vehicle speed are shown in Figure 5 (d) and (g), which are extreme values that typically do not occur.

Optimization of the damping coefficient

After determining k_s=400 N/mm, the initial damping coefficient is multiplied by an element of the set given in given in Equation (17), yielding various curves of suspension performance indexes as damping coefficients varies by using the parametric Simulink model of mixed road surfaces, as shown in (Figure 6). Specifically, Figure 6 (a-e) and (g-h) display the curves of these indexes as damping coefficients, while Figure 6 (f) and (i) show the variations in suspension frequency and damping ratio with respect to damping coefficients.

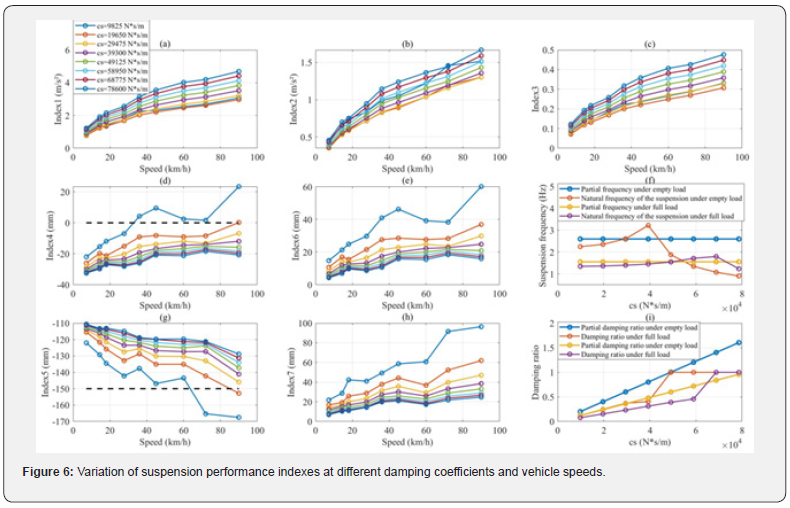
According to (Figure 6), it can be observed that:
1) Index1, Index2 and Index3 increase with increasing damping coefficient, as shown in Figure 6 (a-c). Therefore, a lower suspension damping coefficient is favorable for these indexes.
2) Index6 and Index7 decrease with increasing damping coefficient, as shown in Figure 6 (e) and (h). It indicates that for these two indexes, higher suspension damping coefficient is beneficial.
3) Considering the suspension travel design requirements, the minimum deformation of the suspension should exceed -150 mm, and the maximum deformation of suspension should be less than 0. According to Figure 6 (d) and (g), the permissible damping range is determined to be greater than 19.65 N/mm.

To obtain the minimum Index1, Index2 and Index3, c_s=27 N·s/mm is a better choice under the requirements of suspension travel design and dynamic deformation. It is determined from Figure 6 (f) and (i) that: the partial frequencies of the suspension system under the empty and full loads are about 2.60 and 1.55 Hz, respectively; the partial damping ratio is approximately 0.320 and 0.550, respectively.

Optimization of the ratio of tension-compression damping

After determining k_s=400 N/mm and c_s=27 N·s/mm, the ratio can be changed by an element of the set given in Equation (18), yielding various curves of suspension performance indexes as ratio of tension-compression damping varies by using the parametric Simulink model of mixed road surfaces, as shown in (Figure 7). Specifically, Figure 7 (a-e) and (g-h) display the curves of these indexes as ratio of tension-compression damping, while Figure 7 (f) and (i) show the variations in suspension frequency and damping ratio with respect to ratio of tension-compression damping.

According to (Figure 7), it can be observed that:
1) Index1, Index2 and Index3 are little affected by the ratio of the tension-compression damping, as shown in Figure 7 (a-c). With the ratio of tension-compression damping, they increase slightly.
2) Index6 and Index7 signally decrease with increasing the ratio of the tension-compression damping, as shown in Figure 7 (e) and (h). It indicates that for these two indexes, the higher the ratio of the tension-compression damping is beneficial.
3) Considering the suspension travel design requirements, the minimum deformation of the suspension should be greater than -150 mm, and the maximum deformation of suspension should be less than 0. According to Figure 7 (d) and (g),the permissible ratio range of the tension-compression damping is determined to be less than 1.5.

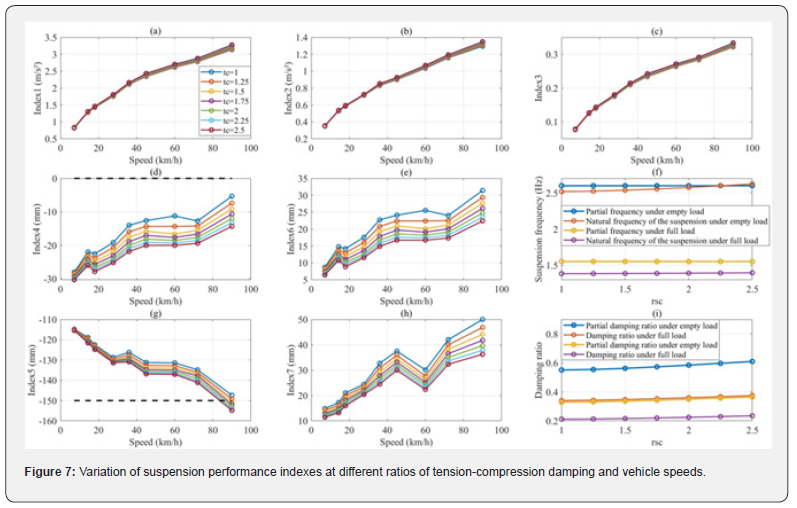
To obtain the minimum Index1, Index2 and Index3, rtc=1.5 is a better choice under the requirements of suspension travel design and dynamic deformation. Therefore, the optimal tension and compression damping coefficients are 33.07 and 22.05 N·s/mm, respectively. At this point, it is determined from Figure 7 (f) and (i) that the partial frequencies of the suspension system under the empty and full loads are about 2.60 and 1.55 Hz, respectively; the partial damping ratio is approximately 0.33 and 0.56, respectively.

Conclusion

1. A graphical method for suspension performance evaluation and parameter matching analysis is proposed. Based on the initial empirical selection of stiffness and damping, a parametric Simulink model for multi-criteria analysis with hybrid road surfaces is established. By varying parameter coefficients, simulation results of various suspension performance indexes under different vehicle speeds and operating conditions are obtained. This approach facilitates the graphical display of performance indexes and suspension performance evaluation, providing a comprehensive basis for matching suspension parameters.
2. The method overcomes the limitations of matching parameters in the empirical frequency-domain by developing an iterative optimization strategy. It combines the advantages of the qualitative selections in the frequency domain and the quantitative evaluations in the time domain. An iterative matching process is presented, progressing from initially selected stiffness and damping coefficients to optimally refined stiffness, damping coefficients, and further to the optimal ratio of the tensioncompression damping, which achieves the optimal comprehensive performance of suspension systems.
3. A method for the matching analysis of the tensioncompression damping coefficients is presented. This study defines the ratio of tension-compression damping and, in conjunction with the optimized damping coefficient, investigates the variation patterns of various performance indexes, establishing a quantitative evaluation basis for different ratios of tensioncompression damping.