Research Article

Mechanical Analysis of Head Impact

Mahmoud Razzaghi*

MRT Research Centre, USA

Submission: December 10, 2018; Published: March 25, 2019

*Corresponding author: Mahmoud Razzaghi, MRT Research, 27862 Manor Hill Rd, Laguna Niguel, CA 92676, USA

How to cite this article: Mahmoud Razzaghi. Mechanical Analysis of Head Impact. Open Access J Neurol Neurosurg. 2019; 10(3): 555787. DOI: 10.19080/OAJNN.2019.10.555787.

Abstract

Objective: To analyze the acceleration of the brain in direct head impact and find the areas of brain most vulnerable to concussion (MTBI).

Method: First, the modes of head and brain acceleration are analyzed. Then, formulas are derived to find the values and effects of rotational accelerations and forces acting on the brain. Comparison is made between modes of acceleration.

Results: With a direct impact, the head will mainly undergo rotational acceleration in the form of spin and whiplash. The highest radial and tangential force and damage occur in the middle of the brain in head spin, and the base of the brain in whiplash. Under equal impact moment, maximum spin radial force is about 3 times that of whiplash while maximum spin and whiplash tangential forces are nearly equal.

Conclusion: Concussion symptoms related to brain function in the middle and base of the brain can be attributed to rotational effects of head impact. Brain is more vulnerable to spin than whiplash. Usually, both spin and whiplash are present together.

Keywords: Concussion; MTBI; Brain Trauma; Head Impact

Introduction

The dynamics of inertial head impact and its interaction with brain is highly complex and a matter of continuing research and debate [1-6]. Finite Element Analysis of head impacts and their relation to Mild Traumatic Brain Injury (MTBI) have been performed using anatomic brain models. This paper provides a high-level perspective on the head movement and the resulting forces on the brain due to a direct blunt impact. A simplified model is used to derive closed form formulas and find forces acting on the brain and the expected areas prone to injury.

Materials & Methods

First, the modes of head and brain acceleration are analyzed. Then, formulas are derived to find the values and effects of rotational accelerations and forces acting on the brain. Comparison is made between modes of acceleration. The head is attached to the body with rotational joints. Therefore, upon a direct blunt impact, it gains rotational acceleration in the form of spin around the neck axis (Figure 1), and whiplash (Figure 2), through rotation around head pivot joint and bending of the neck. If the impact force passes through the neck axis or head pivot joint, there will be no spinning of the head. The force will only rotate the head in whiplash mode both around the head pivot joint and through the bending of the neck in the plane of the force and neck axis [1-5].

A force passing through the center of gravity of a free body does not rotate it. However, due to the anatomy of head and neck, a force passing through the center of gravity of the head has lever age relative to the head pivot joint and rotates the head. As the head spins around the neck axis, it pushes against the brain cortex at the impact site. This produces a pressure wave which propagates through the soft brain resulting in spinning of the brain. Spinning of the brain creates a centrifugal force within its body. The cells farther from its center of rotation pull out with higher centrifugal force. These differential pulls add up to a maximum around the axis of rotation and cause radial tension on brain tissues that may strain and damage them. In whiplash, the whole brain rotates with maximum linear speed at the top of the brain and minimum linear speed at the base of the brain. As a result, the varying centrifugal forces in the brain cause tension in the brain with maximum value at its base [6-10].

The angular acceleration of the head causes change in both direction and value of rotational velocity. The change in direction of velocity is responsible for radial or centrifugal acceleration. The change in the value of velocity is responsible for tangential acceleration. In a similar way as explained for radial acceleration, the tangential acceleration causes shear forces within the brain which is a maximum at the center of rotation of the brain. According to the above analysis, assuming the brain as a continuum medium with uniform density and strength, we should expect brain damage due to impact to occur generally in the cortex, middle, and base of the brain.

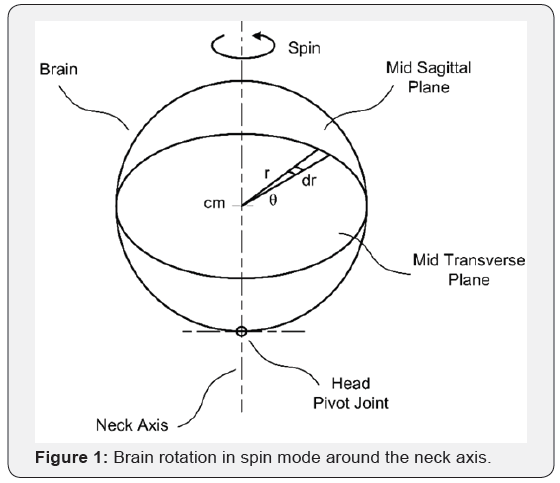
In spinning, the brain rotates around an axis approximately at its center of mass. The plane of spin and related accelerations and forces is a transverse plane. When the head is upright, the spin plane is horizontal.

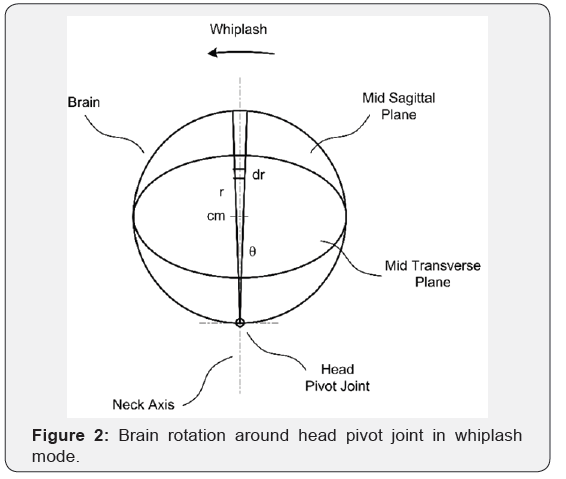
In whiplash, the whole brain rotates around an axis outside of the brain and below the skull. The whiplash accelerations and forces are in a plane perpendicular to the transverse plane. When the head is upright, the whiplash plane is vertical. In a simplified model, the brain is considered as a continuum sphere with radius R, uniform density ρ, and mass M. The spinning mass moment of inertia Is of the brain about an axis through the center of mass is

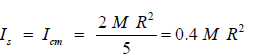
where cm denotes center of mass.

According to Steiner parallel axis theorem, head moment of inertia has the smallest value relative to head pivot joint as compared to lower neck joints. Head pivot joint system has also lower muscle stiffness than the rest of the neck. Therefore, head rotation in whiplash is mainly around the bottom of the skull or head pivot joint especially during the primary acceleration. Using Steiner parallel axis theorem, the mass moment of inertia of the brain around an axis through the head pivot joint and perpendicular to the neck axis in whiplash mode I_w is

Therefore, the moment of inertia of the brain in whiplash is 3.5 times that of spin. The brain accelerates more easily in spin compared to whiplash mode.

The relation between impact moment or torque and the head acceleration is

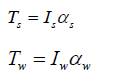
where , T_s , α_s , T_w and α_w denote spin and whiplash torque and angular acceleration respectively. For equal impact torque we will have

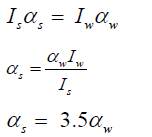
As a result, the spin rotational acceleration of the head or brain would be 3.5 times that of whiplash. With equal impact torque and time period after the impact, the spin rotational speed of the brain ω_s would also be 3.5 times that of the whiplash ω_w.

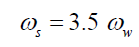
The angular acceleration of the head causes changes in both direction and value of rotational velocity. The change in direction of velocity is responsible for radial or centrifugal acceleration. The change in the value of velocity is responsible for tangential acceleration. In fact, it is the tangential acceleration component of head rotation that is measured with sensors aligned with the skull [9,10].

The centrifugal force is defined by the formula

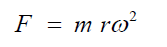
where m, r, and ω are mass, radius of rotation and angular speed of rotation respectively. The centrifugal force is zero at the center and maximum at the extremity of rotation, which causes radial tension within the soft deformable brain. Therefore, maximum radial tension or pull on brain cells occurs at the center of the brain in spin mode and bottom of the brain in whiplash mode.

Consider a slice of the brain in the mid transverse plane with a thickness of t and an angle of θ radians extending from the center of rotation to the periphery of the brain as in Figure 1. The mass m of an element of the slice between radii r and r+ dr is

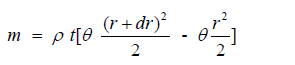
where dr is an infinitesimal change in radius.

Expanding (r + dr)² and ignoring negligible second power of

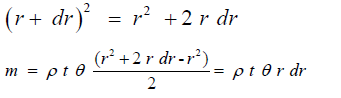
For spin mode, the radial centrifugal forces on the slice elements add up to a maximum F_rsmax at the center of rotation of the slice

Similarly, referring to Figure 2 the maximum whiplash force F_rsmax is in the whiplash plane at the respective center of rotation as

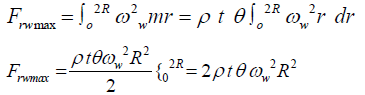
Comparing spin and whiplash forces

F_rsmax = 3F_rsmax

Therefore, under equal conditions of impact torque or moment, maximum radial force and stress in spin mode are 3 times those of whiplash.

The weight of the brain is negligible compared to the inertial impact forces and is ignored in the calculations.

The tangential acceleration is

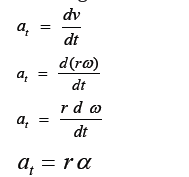
The tangential acceleration increases with radius, which causes shear stress and strain within the brain with maximum values around the center of rotation and mid transverse plane, or mid brain

The tangential accelerations a_ts in spin and a_tw in whiplash are

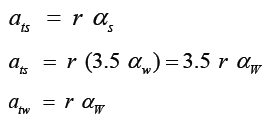
Comparing the two accelerations

a_ts = 3.5a_tw

So, both radial and tangential accelerations in spin mode are 3.5 times those of whiplash. The overall accelerations have the same ratio as shown below

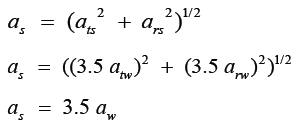
The impact subjects the brain to a radial force and a tangential force, both increasing with distance from the axis of rotation. Therefore, the maximum overall forces from the bulk of the brain are exerted around its center of rotation in the mid transverse plane.

For a slice of the brain at the mid transverse plane with thickness t and an angle θ radians extending from the center of rotation to the periphery of the brain, Figure 1, the maximum tangential force in spin mode F_tsmax is

For a similar slice of the brain in the whiplash plane, Figure 2, the maximum tangential force in whiplash mode F_twmax is

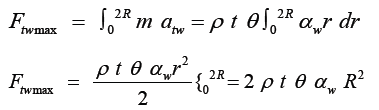
Comparing the spin and whiplash tangential forces

F_twmax = 1.14F_tsmax

Therefore, maximum tangential forces in whiplash and spin are nearly equal.

Results

With a direct impact, the head will mainly undergo rotational acceleration in the form of spin and whiplash. The highest radial and tangential force and damage occur in the middle of the brain in head spin, and the base of the brain in whiplash. Under equal impact moment, maximum spin radial force is about 3 times that of whiplash while maximum spin and whiplash tangential forces are nearly equal.

Discussion

Many concussion symptoms are related to trauma in the middle and base of the brain. The tissues in these areas are cushioned by the surrounding brain mass against any incoming pressure wave in linear acceleration. But in rotation, according to the present analysis, the same brain mass exerts maximum shear and tensile stress on these tissues. A good example of concussion due to head rotation is the devastating effect of hook punch in boxing. There has been a debate on whether linear or rotational acceleration cause brain trauma [3, 11-15]. Pure linear acceleration of the bulk of the brain is a rare occasion. Two specific conditions are when the face or back of the head hits a surface parallel to the frontal plane. Evidently, any form of trauma can happen depending on the severity of the impact.

In most cases, the apparent linear acceleration is actually the tangential acceleration component of the head rotation. An exclusive correlation cannot be established between concussion and merely a single form of acceleration as all forms of acceleration correlate with the impact energy. Therefore, other aspects should be taken into account. Brain deforms little under pressure. Therefore, translational pressure gradients produce much smaller strains compared to tension and shear of rotational accelerations. If rotation of head is prevented, it will be hard to cause traumatic unconsciousness [11, 13].

According to finite element analysis of concussive cases in NFL, concussion occurs after the primary momentum transfer [6,7]. This suggests that during this time the effect of rotational acceleration has reached the middle and base of the brain and affected those areas. An increase in neck strength and stiffness reduces the risk of concussion [6], which means a stiffer neck reduces head rotation and indicates that rotation causes the concussion. Experiments on head whiplash in primates have shown that rotation and contact at impact site equally share the effects of brain trauma [14].

Conclusion

Based on the presented head and brain model the following conclusions can be made Rotational acceleration is responsible for local trauma in the middle and base of the brain. In other words, concussion symptoms related to brain function in these areas can be attributed to rotational effects of head impact.

Brain areas most vulnerable to concussion in spin are

a. The cortex due to transfer of forces between the brain and the skull.

b. Middle of the brain due to radial tension and tangential shear.

Brain areas most vulnerable to concussion in whiplash are

a. The cortex due to transfer of forces between the brain and the skull.

b. The base of the brain due to radial tension and tangential shear.

Under equal impact moment, maximum spin radial force is about 3 times that of whiplash, while maximum spin and whiplash tangential forces are nearly equal. Generally, brain is more vulnerable to spin than whiplash. Usually, both spin and whiplash are present together with a combination of the above effects.

Since the Steiner parallel axis theorem for moment of inertia applies to any shape, the results of the model also apply to a realistic brain shape.

Practical Implications

The present brain modeling and analysis of head impact have the following implications:

· Provide insight into cause effect relation between head impact and concussion.

· Clarify why most concussion symptoms are related to functional members in the middle and base of the brain although they are cushioned by the brain mass.

· Confirm the experimental studies suggesting rotational acceleration as the main cause of MTBI in contrast to linear acceleration.

References

1. Blaine Hoshizaki, Andrew Post, Marshall Kendall, Clara Karton, Susan Brien (2013) The Relationship between Head Impact Characteristics and Brain Trauma. Neurol Neurophysiol 5:1.
2. Meaney DF, Smith DH (2011) Biomechanics of concussion. Clin Sports Med 30(1): 19-31.
3. Young L, Rule GT, Bocchieri RT, Walilko TJ, Burns JM, et al. (2015) When physics meets biology: low and high-velocity penetration, blunt impact, and blast injuries to the brain, Front in Neurol 6:89.
4. Hardy WN, Khalil TB, King AI (1994) Literature review of head injury biomechanics. Int J Impact Eng 15(4):561-586.
5. Post A, Hoshizaki TB (2012) Mechanisms of brain impact injuries and their prediction: a review. Trauma 14(4): 327-349.
6. Casson IR, Pellman EJ, Viano DC (2008) Concussion in the national football league: an overview for neurologists. Neurol Clin 26 (1): 217- 241.
7. Viano DC, Casson IR, Pellman EJ, Zhang L, King AI, et al. (2005) Concussion in professional football: brain responses by finite element analysis: part 9. Neurosurgery 57(5): 891-916.
8. Franklyn M, Fildes B, Zhang L, Yang K, Sparke L, et al. (2005) Analysis of finite element models for head injury investigation: reconstruction of four real-world impacts. Stapp Car Crash J 49:1-32.
9. Crisco JJ, Chu JJ, Greenwald RM (2004) An algorithm for estimating acceleration magnitude and impact location using multiple nonorthogonal single-axis accelerometers. J Biomech Eng 126(6): 849-854.
10. Manoogian, Sarah J (2005) Analysis of linear head accelerations from collegiate football impacts. Master of Science thesis.
11. Ommaya AK, Gennarelli TA (1974) Cerebral concussion and traumatic unconsciousness, Correlation of experimental and clinical observations of blunt head injuries. Brain 97(4): 633-654.
12. King, Albert I, Yang, King H, Zhang, et al. (2003) Is head injury caused by linear or angular acceleration? IRCOBI Conference, Lisbon.
13. Svein Kleiven (2013) why most traumatic brain injuries are not caused by linear acceleration but skull fractures are. Front Bioeng Biotechnol 1: 15.
14. Ommaya AK, Hirsch AE (1971) Tolerances for cerebral concussion from head impact and whiplash in primates. J Biomech 4 (1): 13-21.
15. James Michio Clark, Andrew Post, Thomas Blaine Hoshizaki, et al. (2015) Determining the relationship between Linear and rotational acceleration and MPS for different magnitudes of classified brain injury risk in ice hockey, IRCOBI Conference.