Open Access Ophthalmology Journal

Mini Review

Free-Form Lenses: Why My Patient is Not Wearing My Prescription?

Eva Chamorro*, Jose Alonso, Jose Miguel Cleva and Daniel Crespo

Indizen Optical Technologies SL, Spain

Submission: February 07, 2017; Published: February 27, 2017

*Corresponding author: Eva Chamorro, Wearers Trial Department, Indizen Optical Technologies SL, Santa Engracia, 6-1. 28010 Madrid, Spain, Tel: ; Email: evachamorro@iot.es

How to cite this article: Eva C, Jose A, Jose M C, Daniel C. Free-Form Lenses: Why My Patient is Not Wearing My Prescription?. JOJ Ophthal. 2017; 2(1): 555577. DOI: 10.19080/JOJO.2017.02.555576

Abstract

It is common for patients to return for a revised consultation and on checking the lenses with the lensometer it can be observed that the power of the lenses differs to that prescribed in the original visual examination. Did the eye care practitioner (ECP) change the prescription? At other times, when checking the quality of a single-vision (SV) lens from the central area to the periphery the power of the lens changes dramatically. Is there any problem in the manufacturing process? The reason why the lenses have been manufactured with a power different than the one prescribed is a consequence of the correction of oblique aberrations in free-form lenses. In this paper a short review is presented about how the ophthalmic industry has evolved to improve the visual performance of the user by creating customized lenses according to the characteristics of each patient.

Keywords: Oblique aberrations; Free-form lenses; Base curve; User compensation

Abbreviations: ECP: Eye Care Practitioner; PAL: Progressive Addition Lenses; SV: Single-Vision

Introduction

Ophthalmic lenses compensate for refractive errors, but also produce aberrations. Seidel [1], in 1955 described 5 types of monochromatic aberrations affecting standard imaging systems as cameras, telescopes and microscopes: spherical aberration, coma, curvature of field, distortion and oblique astigmatism [1]. However, an ophthalmic lens has particular properties that require a slightly different approach. Instead of being used at full field, the ophthalmic lens is scanned by the eye behind it. For any gaze direction, only a small portion of the lens is used to create the foveal image. This portion approximately has the size of the pupil and it is located at the point where the visual axis crosses the lens. The consequence is that Seidel aberrations affect lens performance differently to the way they would do in standard imaging systems. In particular, curvature of field and oblique astigmatism produce the joint oblique aberrations, causing the lens to deliver a different than expected power when viewing through the lens at oblique directions. Oblique aberrations appear when rays of light from an object go through the lens at an oblique angle, for example, when a patient is looking away from the optical center using the peripheral area of the lens or when the lenses are not fitted completely perpendicularly to the viewing direction of the patient. In these situations, the lens is effectively providing a prescription with incorrect values of sphere, cylinder and axis, causing blurry vision and loss of visual field.

Conventional production of lenses is based on the usage of a small number of different molded blanks with specific power characteristics on the frontal surface of the lens and generating the wearer’s prescription on the back side by shaping a sphere or torus. Using molded blanks with spherical geometry, it is possible to either reduce the astigmatic or the spherical component of the oblique aberration by selection of the best-form base curve (which is the name we use for the frontal surface) according to Tscherning’s theory. In other words, given the lens refractive index and the user prescription, there is a value for the dioptric power of the frontal surface of the lens that minimizes the oblique aberrations. For example, according to Tscherning’s theory, a lens with a prescription of +2D should be produced with a base curve of 7.50D in order to minimize oblique astigmatism [2,3].

However, in practice, this selection of base curve has some limitations. First, the recommended base curve, according to Tscherning’s theory, is too curved and leads to thicker and heavier lenses and, in consequence, less ergonomic glasses with a worse aesthetic appearance. Secondly, the best form lenses require labs to keep a wide stock of molded blanks with base curves adapted for each prescription which increases the cost of the manufacturing process. In order to avoid some of the limitations of spherical base curves, it is possible to use a spherical base curves that allow the production of flatter and thinner lenses with an acceptable reduction of oblique aberrations. However, there are still important limitations because the conventional production does not allow different asphericity levels as required by the prescription. In addition, lens tilting by pantoscopic or wrapping angles as well as grinded prisms by decentration is not recommended in aspheric lenses. So, the use of aspherical molded blanks is basically helpful in improving the aesthetics of the lens.

In recent years, the way in which the lenses are manufactured has changed significantly through the introduction of free-form technology. In comparison with the conventional manufacturing processes that only allow the generation of a sphere or torus on the back surface of the lens, free-form technology allows the production of arbitrary surfaces. So, the combination of spherical molded blanks with a back surface produced point by point allows a much better compensation of the oblique aberrations. Further, it is possible to compensate the oblique aberrations according to the tilt of the lens. In other words, it is possible to optimize the lens for all gazes, according to the visual requirements of each patient and the specification of the frame shape and tilts, that is, to provide a full customization of the lens design. Thanks to sophisticated optical design software, it is possible to calculate the unwanted sphere and cylinder power errors (oblique aberrations) that decrease the visual quality for patients. 0ptimization algorithms will optimize the back lens surface to compensate for oblique aberrations taking into consideration all the factors involved: lens refractive index, prescription, base curve, frame characteristics and the position of wear of each patient (interpupilary distance, fitting height, back vertex distance, pantoscopic angle, wrapping angle or near working distance). The result is a user-compensated lens (SV, bifocal or PAL) with an individual back surface customized for the wearing position of each patient.

So, how does a customized lens perform when measured in a lensometer? It is important to note that the lensometer measures the power of ray beams perpendicular to the back surface of the lens. This classic configuration matches the power perceived by the user only for central vision and when the lens is fitted with no tilts. Due to the compensation of oblique aberrations for all gaze directions, the lens may present varying local differences in power in relation to the original prescription. When checking the lens with the lensometer, powers can be altered at the reference points: the optical center for SV lenses or the distance and near reference points for PALs. In addition, in the case of SV lenses, where constant power values over the whole lens would be expected according to the conventional manufacturing process, we can measure significant power differences at different points on the lens. However, it is important to consider that these variations of power ensure that the patient has the best prescription when looking through the different areas of the lens, improving the visual, even in its peripheral areas.

Discussion

The effect of oblique aberrations and their compensation in the user’s visual performance can be analyzed from a theoretical point of view or by wearer trials that evaluate the satisfaction rates of the final user. A theoretical analysis can be done by modelling both the lens-eye and the lens-lensometer systems by means of exact ray tracing. A dense grid of points is created on the lens and the power at each point computed for both systems. The results can be compared by the use of sphere and cylinder maps showing the power measured by the lensometer and the power perceived by the user. For example, in Figure 1 a theoretical comparative analysis is presented of a user compensated SV free-form lens and the corresponding conventional SV lens.

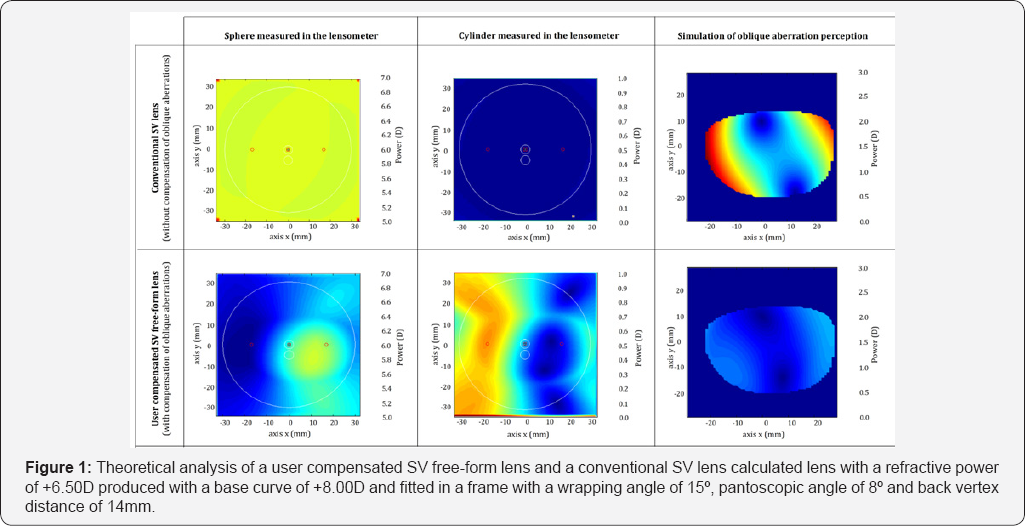
The lens has a refractive power of +6.50D, produced with a base curve of +8.00D and fitted in a frame with a wrapping angle of 15°, pantoscopic angle of 8° and back vertex distance of 14mm. As expected, the lensometer power of the conventional lens is constant (both sphere and cylinder) all over the surface of the lens. However, the cylinder of the user perceived power grows above 2 D at both the nasal and temporal sides as a consequence of the strong oblique aberrations produced by this combination of power, base curve and tilts. The area without significant aberration is reduced to two points in the central area of the lens. On the other hand, for a free-form SV lens compensated according to the individual personalization data of the patient, the spherical and cylinder power change point by point all over the surface of the lens. Measured power in the optical center is +6.42sph, -0.29cyl x 114°. However, the aberration perceived by the user is largely reduced, providing a much wider and clear field of view and thus, more comfort. We should stress here that “user-perceived power” does not mean a subjective perception of optical power, but the actual vergence of the light beams entering the eye for any gaze direction when the lens is positioned “as worn”. So any user-perceived power different than the actual prescription will automatically yield a reduction of visual acuity.

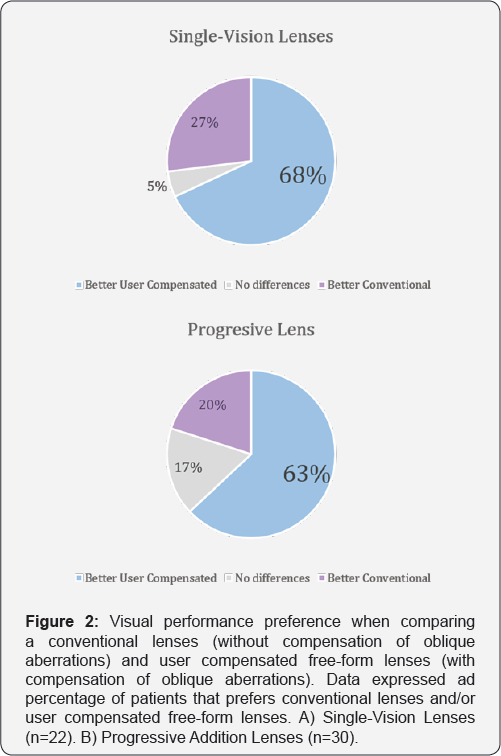
In addition to the theoretical analysis of the user perception, different randomized double-masked wearer trials have been carried out by our research group in order to compare the visual performance of conventional lenses (without compensation of oblique aberrations) and user compensated free-form lenses (with compensation of oblique aberrations). The performance of user compensated SV lenses was tested in 22 subjects aged between18 and 40 years. Refractive errors were between +4.00 and -8.00D with astigmatism lower than 2.00D. Patients were asked to wear 2 different pairs of glasses over a period of time and select their preferred choice. Tested lenses were: 1) A conventional sphero cylindrical SV lens using a standard base curve selection and 2) a free-form SV customized for each patient and produced with the flatter possible base curve. Results showed a clear preference for free-form lenses: 68% of patients selected free form SV lenses, 27% selected the conventional SV lens and 5% of the patients did not perceived differences between both designs [4].

Secondly, the satisfaction of user compensated PAL was tested in 30 presbyopic individuals aged between 45 and 65 years with refractive errors between +4.00 and -6.00D with astigmatism lower than 2.50D. Patients wore 2 PAL designs developed ad-hoc for the study with the same power distribution but different optimization methods for the compensation of oblique aberrations as follows: A) Lens optimized with a merit function that tries to match lensometer power to the prescription and B) Lens optimized according to the user personal parameters with a merit function that tries to match user-perceived power to the prescription. After using each design for 7 days, patients were asked to select their preferred design. Results showed that 63% of subjects preferred the user compensated lens, 20% preferred the conventional lens and 17% did not perceived differences, indicating a clear preference for user compensated lenses [5,6] (FIgure 2).

Conclusion

New manufacturing technologies of lenses have allowed new calculation methods that compute and compensate the unwanted sphere and cylinder power errors (oblique aberrations) that decrease the visual quality of the patients. Consequently, the measured power in the lensometer of user compensated lenses varies at each point of the lens and can be significantly different to the original prescription. Theoretical and clinical analyses have demonstrated the efficacy of the compensation of the oblique aberrations to improve the visual quality and satisfaction of patients.