Research Article

Modeling and Simulation of a High Strength and High-Temperature Resistant Composite Structure Material for In-Space Optical Mining Applications

Hadarou Sare and Dongmei Dong*

Department of Material Sciences and Engineering, Rowan University, Glassboro, USA

Submitted: January 02, 2024; Published: February 13, 2024

*Corresponding author: Dongmei Dong, Department of Material Sciences and Engineering, Rowan University, Glassboro, USA

How to cite this article: Hadarou Sare and Dongmei Dong*. Modeling and Simulation of a High Strength and High-Temperature Resistant Composite Structure Material for In-Space Optical Mining Applications. JOJ Material Sci. 2024; 8(3): 555738. DOI:10.19080/JOJMS.2024.08.555738

Abstract

In this paper, the modeling and simulations of a high-strength and high-temperature resistant composite structure material for in-space optical mining (asteroid mining) are investigated. The investigation consists of:

a) investigation of the mechanical performance (high strength) of a composite structure material for in-space optical mining

b) investigation of the thermal performance (high-temperature resistant) of a composite structure material for in-space optical mining. COMSOL, a finite element analysis software is used to model and simulate the composite structure material. As part of the mechanical investigation, three different methods are used to model the composite structure: Layerwise theory, Equivalent Single Layer (ESL) theory, and a multiple model method. Modal and frequency-response analyses are performed for the specified loading and the multiple model method is compared with the traditional layerwise and ESL theory in terms of performance and accuracy in the results, including through-thickness stress distribution.

As part of the thermal investigation, a virtual experiment is set up in COMSOL where the composite structure material is heated up by a laser that moves radially in and out over time while the composite material itself rotates on its stage. Modeling the incident heat flux from the laser as a spatially distributed heat source on the surface, the transient thermal response of the material is obtained. The peak, average, and minimum temperatures during the heating process are computed, as well as the temperature variations across the material.

The originality and contributions of this work are listed as follows:

a) novel material development for in-space optical mining application. This work introduces a new composite material with exceptional high-strength and high-temperature resistance tailored specifically for in-space optical mining. The formulation of this material could involve innovative combinations of polymers, ceramics, or other advanced materials.

b) integration of composite material with optical mining systems. This work shows the development of simulation models that integrate composite material into the overall optical mining system. This includes considering the interaction of the material with mining tools, energy sources, and other components to optimize the entire mining process.

c) thermal management solutions for the optical mining environment. This work shows innovative solutions for thermal management in high-temperature environments encountered during optical mining. This involves simulations that demonstrate how the material effectively dissipates heat or resists thermal degradation, ensuring the durability and longevity of mining equipment. d) understanding the behaviors of materials in the space environment. Specific focus on the unique challenges posed by the space environment, such as micro gravity and vacuum conditions. This work contributes to understanding how the material behaves in these conditions and how it can withstand or adapt to the challenges of space mining.

e) evaluation of the material’s contribution to resource efficiency and sustainability in space operations. This includes considerations of recycling, re usability, and reduced reliance on Earth-based resources for space missions.

f) contribution to interdisciplinary insights. This work will lead to collaboration between researchers from various disciplines, including materials science, aerospace engineering, optics, and mining engineering. The interdisciplinary approach can provide comprehensive insights into the challenges and opportunities associated with in-space optical mining, vii) contribution to future space exploration. The work contributes to the broader field of space exploration by providing solutions for resource extraction and utilization in space, which is crucial for sustainable and long-term human presence beyond Earth.

The findings of this work can be relevant for in-space optical mining (asteroid mining).

Keywords: Modeling; Simulation; Strength; Composite material; Mechanical properties; Thermal properties; Asteroid mining; Space, Stress; Multiple model method; Layerwise theory; ESL theory; Finite element analysis; Heat, Thermal insulation; Temperature

Introduction

Due to the valuable resources asteroids contain, the exploration of asteroids for future mining purposes has received considerable attention [1-3]. For these missions, one needs to consider

a) the spacecraft rendezvous and maneuver phase, during which one needs accurate control of the spacecraft dynamics, when this spacecraft is being navigated in the vicinity of the asteroid that is being captured.

b) asteroid capturing phase.

c) optical mining phase.

Even though rendezvous mission and docking, spacecraft rendezvous and proximity maneuvering [4,5], and spacecraft guidance in rendezvous missions [6] have been studied quite extensively in the literature, asteroid mining without excavation (optical mining) has not received much attention. To address this gap, the primary goal of this paper is to study the modeling and simulations of a high-strength and high-temperature resistant composite structure material for in-space optical mining (asteroid mining). In other words, this paper consists of

a) an investigation of the mechanical performance (high strength) of a composite structure material for in-space optical mining

b) an investigation of the thermal performance (hightemperature resistant) of a composite structure material for inspace optical mining. COMSOL, a finite element analysis software is used to model and simulate the material.

The objective of the mechanical performance investigation is to figure out the best combinations of materials suitable to be used for in-space asteroid mining (optical mining). For this paper, we only show the modeling and simulations of a composite structure material made up of Nomex (outer layer), Kevlar (supporting layer), and Aerogel (core layer).

It is important to mention that multiple combinations made up of the following were modeled and simulated in COMSOL: Nomex, Kevlar, Aerogel, Carbon epoxy, Glass vinylester, Kapton, PVC foam, Polyethylene Terephthalate (PET), Polyamide (Nylon), Polyimide, Aluminized mylar, PTFE (Teflon), Polypropylene, Silica aerogel, High-temperature fabrics, Carbon/carbon composite. Based on the listed materials, the combination of Nonex/Kevlar/ Aerogel stands out as the best combination to be considered as a high-strength composite structure material for in-space optical mining.

The objective of the thermal investigation is to figure out if the selected composite structure material (material made up of Nomex/Kevlar/Aerogel) based on the mechanical performance investigation is suitable to be used for optical mining (asteroid mining). For the thermal performance investigation, a virtual experiment is set up in COMSOL where the material made up of Nomex, Kevlar, and aerogel is heated up by a laser that moves radially in and out over time while the composite material itself rotates on its stage.

First, for the Mechanical investigation, the model compares three commonly used methods [7] for the analysis:

a) An equivalent single layer theory, using first-order shear deformation theory (ESLFSDT).

b) a layerwise elasticity theory.

c) a multiple model method.

The ESL theory [7] reduces a 3D continuum to an equivalent 2D description, thereby reducing the size and computational time involved in solving a problem. The first-order shear deformation theory (FSDT) is implemented in the Layered Linear Elastic Material model in the Shell interface. The layerwise elasticity theory [7] is implemented in the Layered Shell interface. The theory considers a composite as a 3D continuum, giving a more accurate resolution of stresses and strains, particularly in the through-thickness direction.

The ESL and layerwise theories each have advantages and disadvantages, in terms of solution accuracy and solution time, for different types of problems. By judiciously combining the use of the two theories in a single model, it is possible to obtain high accuracy results, at a low computational cost. The approach of combining the theories in this way is called a multiple model method, or a global-local analysis.

Second, for the Thermal investigation, the composite material designed and simulated (mechanical properties simulations) is heated up by a laser that moves radially in and out over time while the composite material itself rotates on its stage. The transient thermal response of the composite material is obtained by modeling obtained by modeling the incident heat flux from the laser as a spatially distributed heat source on the surface. The average, maximum, and minimum temperatures, as well as the peak temperature difference across the composite material, are stored at every calculation step. The temperature distribution across the entire composite material is stored at a specified number of output time steps. The originality and contributions of this work are listed as follows:

a) Novel Material Development for in-space optical mining application. This work introduces a new composite material with exceptional high-strength and high-temperature resistance tailored specifically for in-space optical mining. The formulation of this material could involve innovative combinations of polymers, ceramics, or other advanced materials.

b) Integration of composite material with Optical Mining Systems. This work shows the development of simulation models that integrate composite material into the overall optical mining system. This includes considering the interaction of the material with mining tools, energy sources, and other components to optimize the entire mining process.

c) Thermal Management Solutions for the optical mining environment. This work shows innovative solutions for thermal management in high-temperature environments encountered during optical mining. This involves simulations that demonstrate how the material effectively dissipates heat or resists thermal degradation, ensuring the durability and longevity of mining equipment.

d) understanding the behaviors of materials in the Space Environment. Specific focus on the unique challenges posed by the space environment, such as micro-gravity and vacuum conditions. This work contributes to understanding how the material behaves in these conditions and how it can withstand or adapt to the challenges of space mining.

e) Evaluation of the material’s contribution to resource efficiency and sustainability in space operations. This includes considerations of recycling, re-usability, and reduced reliance on Earth-based resources for space missions.

f ) vi) contribution to Interdisciplinary Insights. This work will lead to collaboration between researchers from various disciplines, including materials science, aerospace engineering, optics, and mining engineering. The interdisciplinary approach can provide comprehensive insights into the challenges and opportunities associated with in-space optical mining.

g) Contribution to Future Space Exploration. The work contributes to the broader field of space exploration by providing solutions for resource extraction and utilization in space, which is crucial for sustainable and long-term human presence beyond Earth.

Results from the mechanical and thermal investigations show that the composite structure material made up of Nomex, Kevlar, and Aerogel can be used as high Strength and high-temperature resistant composite structure material for in-space optical mining applications. The rest of this paper is organized as follows. In Section II, the model developments for both the mechanical and thermal investigations are discussed. In Section III, the equations and parameters for both the mechanical and thermal investigations are detailed. Following that, in Section IV, the results obtained for both the mechanical and thermal investigations are presented and discussed. Finally, concluding remarks are collected together in the last section.

Model Development

Model Definition for the Mechanical Investigation

In this model, we perform an eigenfrequency analysis and a frequency-domain analysis of a composite structure material made up of Nomex (outer layer), Kevlar (reinforcement layer), and Aerogel (core layer), using the three modeling approaches discussed previously:

a) Equivalent single layer theory

b) Layerwise theory

c) Multiple model method, in which the ESL and layerwise theories are combined in the through-thickness direction of the composite material.

Geometry and boundary conditions: The geometry of the composite material made up of Nomex/Kevlar/Aerogel is shown in figure 1 below while the through-thickness view of the material is shown in figure 2 below.

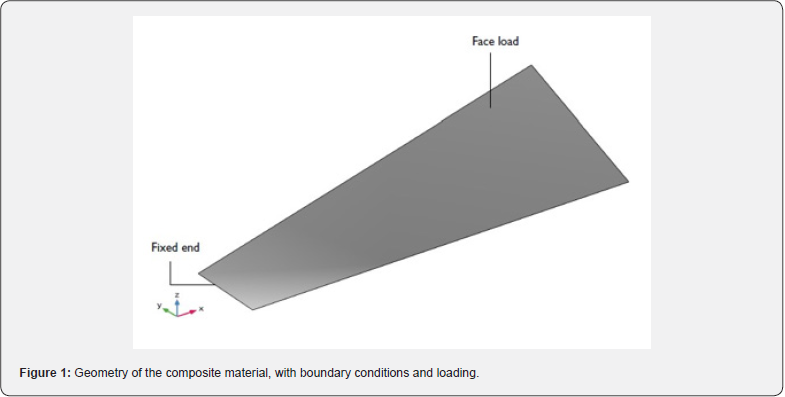
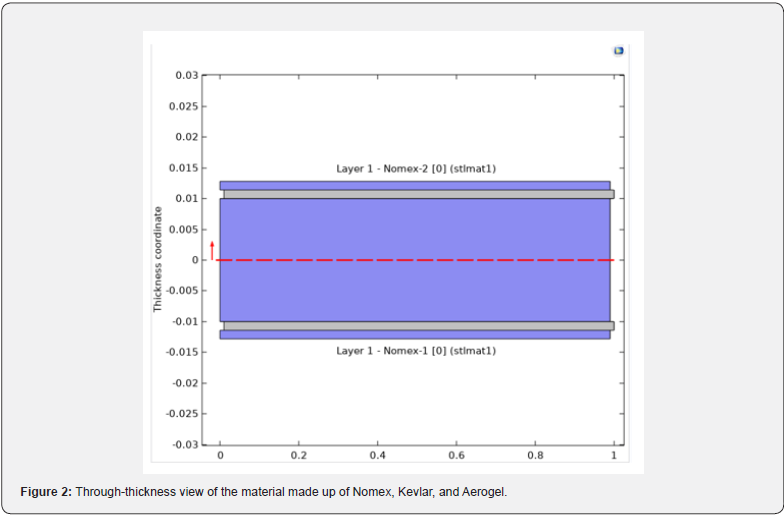
The boundary conditions and loading are:

a) The short end of the composite structure material is fixed.

b) A load is pressure excitation applied on the face of the composite material. The load is entered as a normal component of the boundary load using the expression [7]

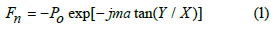
In the above equations, Po is the magnitude of the force Fn, Po is the constant amplitude of the force, j is the Imaginary unit, atan(Y, X) is the Arc tangent function with two arguments, representing the angle whose tangent is the quotient Y and X. Using the magnitude of Po = 104Pa and azimuth mode number m = 3, the excitation frequency is 10Hz.

Material Properties: The composite material is a structure consisting of three different

material types: Nomex (outer layer), Kevlar (reinforcement layer), and Aerogel (core layer).

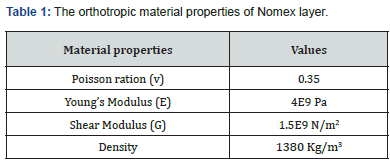
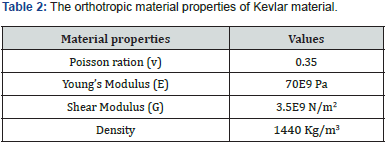
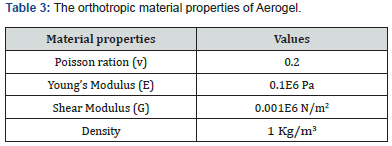
The outer layer of the structure is a single Nomex layer with a thickness of 1.0mm, oriented at 0 degrees to the principal axis. The density of the layer is 1380 kg/m3. The orthotropic material properties are given in table 1 below [8-14]. The next layer of the structure is a Kevlar material with a thickness of 1.0mm, orientated at 0 degrees to the principal axis. The density of the layer is 1440 kg/m3. The orthotropic material properties are given in table 2 below [8-14]. The core material of the structure is an Aerogel of thickness 0.75mm. The density of the layer is 1 kg/m3. The orthotropic material properties are given in table 3 below [8- 14].

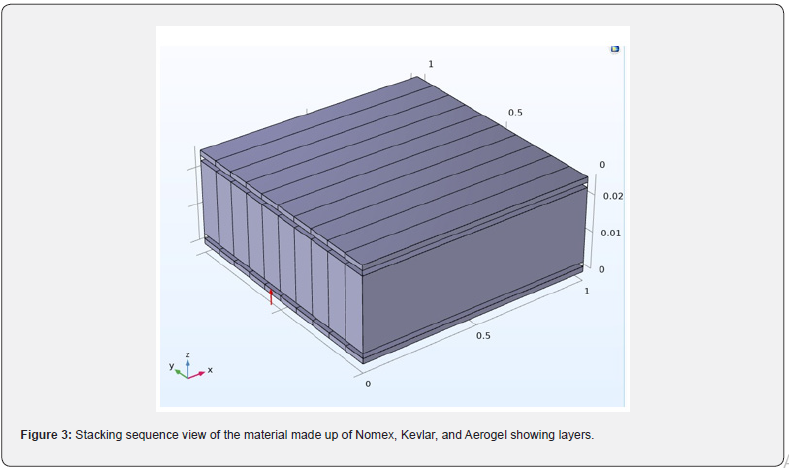
The stacking sequence for the material showing the orientation of each layer (Nomex, Kevlar, and Aerogel), from bottom to top is shown in the figure 3 below.

Finite Element Mesh: The composite material modeled with the Layered Shell is discretized

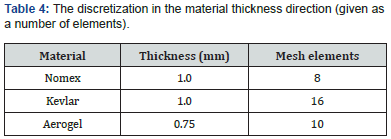
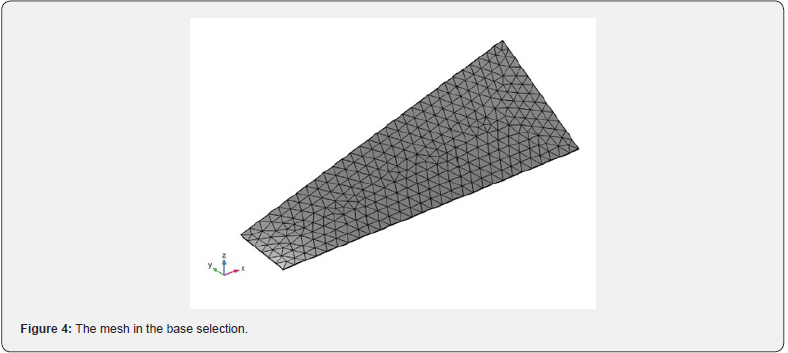
at two levels. The in- plane discretization is done in a standard fashion in the Mesh node in the Model Builder tree. The out-ofplane (thickness) discretization is controlled in the Layered Material node. A triangular mesh is used in the plane, as shown in figure 4. The discretization in the material thickness direction (given as a number of elements) is shown in table 4 below.

Model Definition for the Thermal Investigation

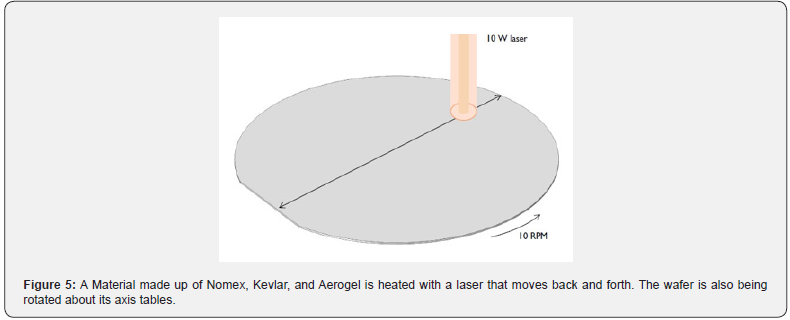
A 2-inch composite material made up of Nomex, Kevlar, and Aerogel, as shown in figure 5, is heated for one minute by a 10 W laser that moves back and forth, while the composite material rotates on its stage. This 2-inch material is from the material modeled and simulated in the mechanical investigation part in sections II-A) above.

Assuming good thermal insulation from the environment, the only source of heat loss is from the top surface via radiation to the processing chamber walls, which are assumed to be at a fixed temperature of 20°C [11-12,14]. The laser beam heat source is modeled as a heat source moving across the surface of the spinning material. To model the rotation of the material, we used the Moving Mesh-Rotating Domain feature in COMSOL software. We use a Waveform function and a set of variables to define the Gaussian distribution of the laser heat load around the focal point, as it moves back and forth across the spinning structure (material). In the results visualization of the temperature profile across the composite material, the results can be visualized in either the spatial frame or the material frame, representing the point of view of an outside observer or an observer moving with the rotation of the composite material, respectively.

The emissivity of the surface of the composite material is approximately 0.8. At the operating wavelength of the laser, it is assumed that absorptivity equals emissivity. The heat load due to the laser is thus multiplied by the emissivity. Assuming also that the laser is operating at a wavelength at which the composite material is opaque, no light is passing through the composite material. Therefore, all of the laser heat is deposited at the surface of the material. The composite material is meshed using a triangular swept mesh. Swept meshing allows for only a single thin element through the thickness and still maintains a reasonable element size in the plane. Also, the solver’s relative tolerance is slightly lowered to better capture the effect of the moving heat load. A finer mesh and tighter solver tolerances would give slightly more accurate predictions of the peak temperature, but predictions of average and minimum temperature would not be greatly affected.

Equations And Parameters

Equations and Parameters for the Mechanical Investigation

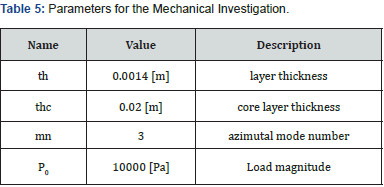
Global Definition Parameters: The thickness for both the Nomex and Kevlar layers is 0.0014 meters while the thickness for the Aerogel (core) is 0.02 meters. Three azimuthal mode numbers are considered and the load magnitude considered is 10000 Pascal. The parameters are summarized in the table below (Table 5).

Equations and Parameters considered for the Multiple Model Method: For the multiple

model method, the eigenfrequency analysis and the frequency domain analysis of the material are performed using the following equations. These equations apply to the linear elastic model of the designed material.

First, for the multiple model method, the equations for eigenfrequency analysis are as follows [7].

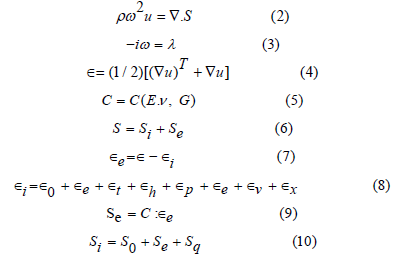
In the above equations, E is the Young’s modulus from the material, ν is the Poisson ratio from the material, G is the shear modulus from the material, and ρ is the density from the material, u is the displacement field, ω is the angular frequency, ∇ is a Del operator representing the gradient, S is the Stress tensor, λ is the Eigenvalue, ϵ is the strain, C is the Elasticity matrix, S is the Total stress, Si is the Initial stress, Se is the Stress due to elastic deformation, ϵe is the Effective strain, ϵi is the Initial strain, ϵ0 + ϵe + ϵt + ϵh + ϵp + ϵc + ϵv + ϵx are Different components of strain, ϵe is the Effective strain, Se is the Stress due to elastic deformation, Sq is the Stress due to plastic (inelastic) deformation.

The top face load equations for both the top and the bottom faces are defined as [7]

where the force FA for both x and y axis are defined to be both 0 N/m2 and the force FA for the z-axis is defined as below

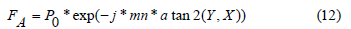
In the above equations, S is the Stress tensor, n is the Unit normal vector to a surface, · is the Dot product, P0 is the Constant amplitude of the force, j is the Imaginary unit, arctan2(Y, X) is the Arc-tangent function with two arguments, representing the angle whose tangent is the quotient of the two specified numbers.

Second, for the multiple model method, the equations for frequency domain analysis are as follows [7].

Second, for the multiple model method, the equations for frequency domain analysis are as follows [7].

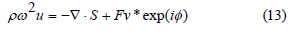
All other equations used in the case of eigenfrequency analysis are applied to the frequency domain analysis case. All other conditions, forces, and constraints used in the case of eigenfrequency analysis are also applied to the frequency domain analysis case. In the above equation, Fν is the Constant amplitude of the external force in the volume, i is the Imaginary unit, ϕ is the Phase angle.

Equations and Parameters considered for both the ESL and Layerwise Theory Methods:

For both the ESL and the layerwise theory methods, the eigenfrequency analysis and the frequency domain analysis of the material are performed using the following equations. These equations apply to the linear elastic model of the designed material.

First, for both the ESL and the layerwise theory method, the only equation for eigenfrequency analysis that changes from the multiple model method is as follows [7].

All other equations (eigenfrequency analysis equations) used in the Multiple Model Method case apply to this case. All other conditions, forces, and constraints used in the Multiple Model Method case also apply to this case. Second, for both the ESL and the layerwise theory method, the only equation for eigenfrequency analysis that changes from the multiple model method is as follows [7].

All other equations (eigenfrequency analysis equations) used in the Multiple Model Method case apply to this case. All other conditions, forces, and constraints used in the Multiple Model Method case also apply to this case.

Equations and Parameters for the Thermal Investigation

Global Definition Parameters: The Nomex/Kevlar/ Aerogel material designed and

considered for the thermal simulation part has the following parameters:

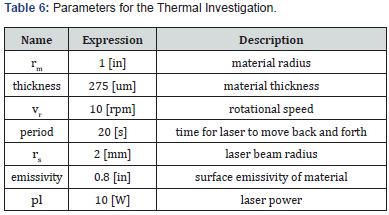
a) the radius of the material is 0.0254 m (1 in).

b) the thickness of the material is 2.75E-4m.

c) the material rotates at a speed of 10 radii per minutes (10 rpm).

d) the time for the laser to move back and fourth is is 20 seconds.

e) the radius for the laser beam is 0.002 meters.

f) the surface emissivity of the material is 0.8.

g) the power for the laser is 10 watts.

The global parameters defined in COMSOL are shown in the table below (Table 6).

Variable Parameters and equations: Assuming that xf is the x location of the laser focal point

and yf is the y location of the laser focal point, the distance from the focal point (rf) and the Gaussian profile of the laser heat flux Flux are defined as follow

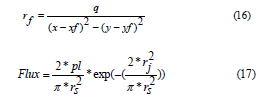
In the above equation, rf is the Distance from the focal point, x is the x-coordinate in the space, y is the y-coordinate in the space, Flux is the Laser heat flux, pl is the Laser power, rs is the Spot size parameter.

Equations and Parameters for Nomex/Kevlar/Aerogel material: From the properties of

each materials defined previously, the following equations could be used to calculate the properties of the combined Nomex/ Kevlar/Aerogel material.

The density could be calculated using the following equation

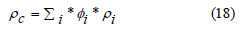
where ϕi is the volume fraction of the material i, ρi is the density of the material i, and ρc is the density of the combined Nomex/Kevlar/Aerogel material.

The Young’s modulus could be calculated using the following equation

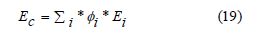
where ϕi is the volume fraction of the material i, Ei is the Young’s modulus of the material i, and Ec is the Young’s modulus of the combined Nomex/Kevlar/Aerogel material.

The Poisson ratio could be calculated using the following equation

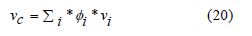
where ϕi is the volume fraction of the material i, νi is the Poisson ratio of the material i, and νc is the Poisson ratio of the combined Nomex/Kevlar/Aerogel material.

The shear modulus could be calculated using the following equation

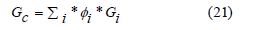
where ϕi is the volume fraction of the material i, Gi is the shear modulus of the material i, and Gc is the shear modulus of the combined Nomex/Kevlar/Aerogel material. Assuming that the volume fraction of the material i is ϕi = 1/3, the properties for the Nomex/Kevlar/Aerogel are summary in the table below (Table 7).

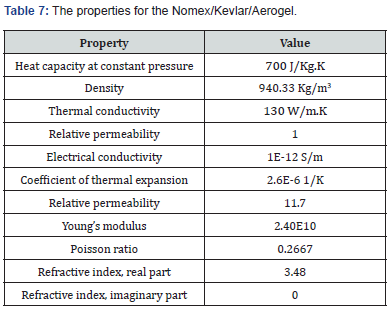
Heat transfer equations and Parameters for Nomex/Kevlar/ Aerogel material: Assuming

that ρ is the density from the material and the Cp is the heat capacity at constant pressure from the material, the timedependent heat equation can be derived from the law of the conservation of energy, seen below in Equation 27:

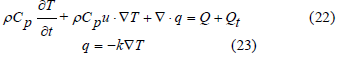
is conducted through the material. The right-hand side of the equation Q + Qt represents any internal or external heat sources that contribute to the overall heat balance in the system.

The thermal insulation equation is formulated as seen below

In the above equation, the term −n · q represents the dot product of the vector n and the vector q. The heat flux equation is established as below

Where

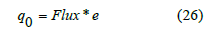
e is the emissivity. The surface-to-ambient radiation equation is formulated as seen below

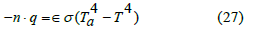
In the above equation, Ta is the temperature of the ambient temperature, ϵ is the surface emissivity, σ is the Stefan-Boltzmann constant, which is a physical constant that relates the intensity of thermal radiation to the temperature of an object.

Simulation and Results

Results for the Mechanical Investigation

The layerwise theory uses three-dimensional kinematics and can predict stresses and strains with high accuracy. The results from using this theory are therefore used as a benchmark. The results from using the ESL theory and the multiple model method are compared with the layerwise theory predictions.

Eigenfrequency Analysis: The first six eigenmodes, using the multiple model method, are

shown in figure 6. The eigenmodes using the layerwise and ESL theories are essentially indistinguishable from the multiple model method eigenmodes, and they are therefore not shown here. However, the computed eigenfrequencies differ between the different modeling approaches. The corresponding six eigenfrequencies are shown in table 8 below for each method.

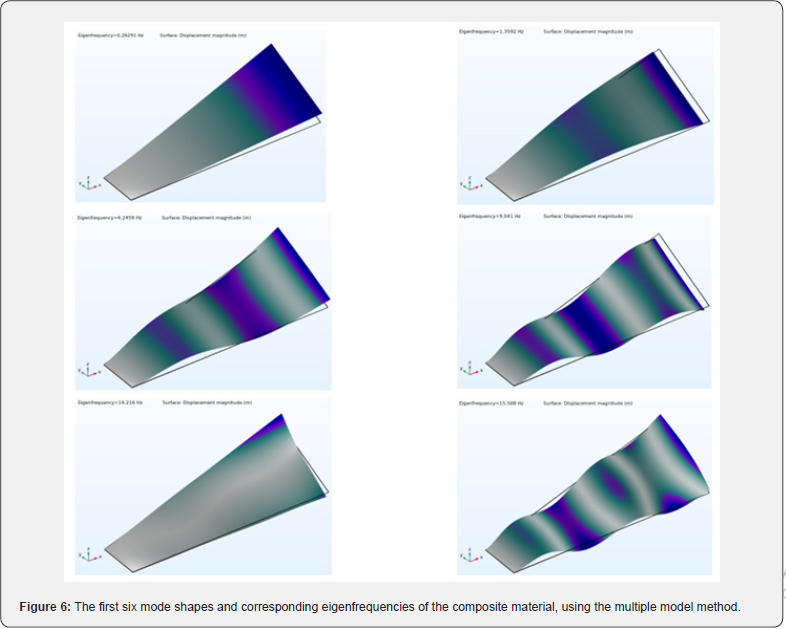
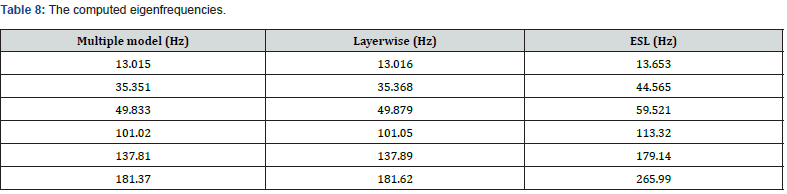
From the above table 8, it can be seen that the computationally less expensive predictions from the multiple model method are in very close agreement with the layerwise values. Predictions using the ESL theory deviate, likely because while the ESL theory is computationally inexpensive, it is less accurate for thick to moderately thick shells. This underscores the computational merit of a multiple-model method, in which thicker parts of a composite material structure are modeled using a layerwise theory, and thinner parts are modeled using the ESL theory.

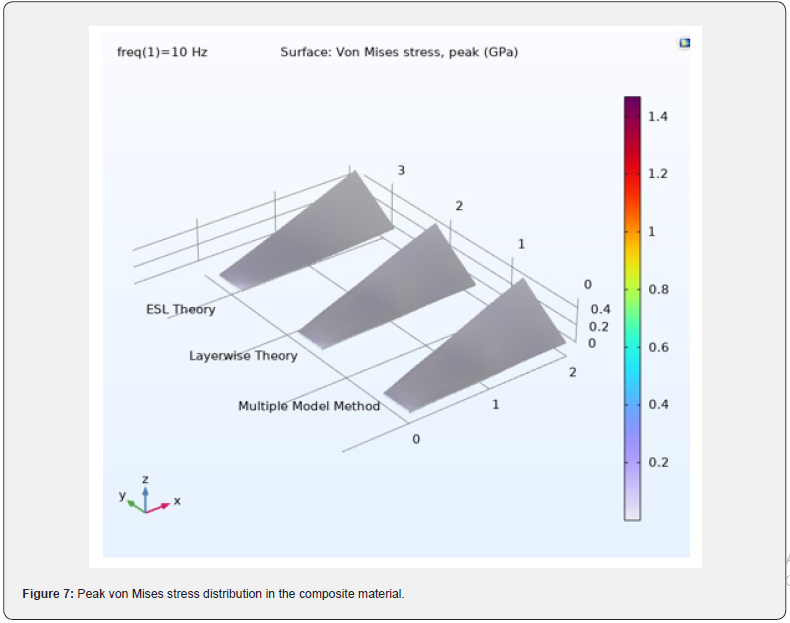
Frequency Domain Analysis: The von Mises peak stress distribution for each modeling

approach is presented in figure 7.

The figure shows that the stress response from the multiple model method closely matches the layerwise case, both in distribution and in peak value. The figure also shows that the stress distribution using the ESL theory differs slightly.

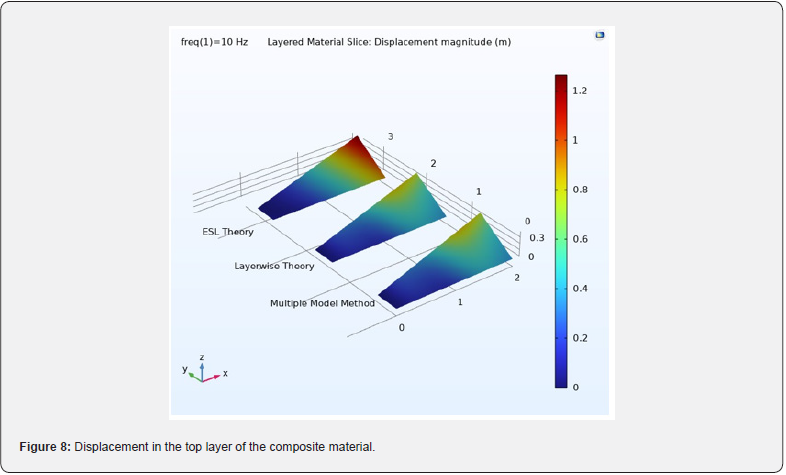
The frequency-domain results in terms of displacements are presented in figure 8 for each modeling approach. Again, the multiple model method approach produces results that are in close agreement with the results from the layerwise theory, while the ESL theory fails to accurately predict the displacement distribution and peak value. The distribution of peak von Mises stress in the through-thickness direction at a particular location is also investigated in this work. The results using the multiple model method and the layerwise theory are in close agreement, while the ESL theory produces different results. This is expected, as the ESL theory is incapable of accurately computing inter-laminar shear stresses in thick composites.

Results for the Thermal Investigation

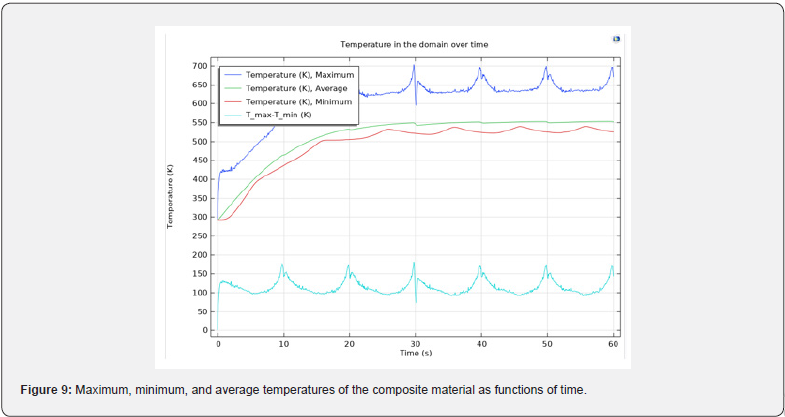
Figure 9 shows the probe plots of the maximum, minimum, and average temperatures of the composite material designed. Figure 10 shows the probe plot of the difference between the maximum and minimum temperatures. The temperature distribution across the composite material is plotted in figures 11 & 12.

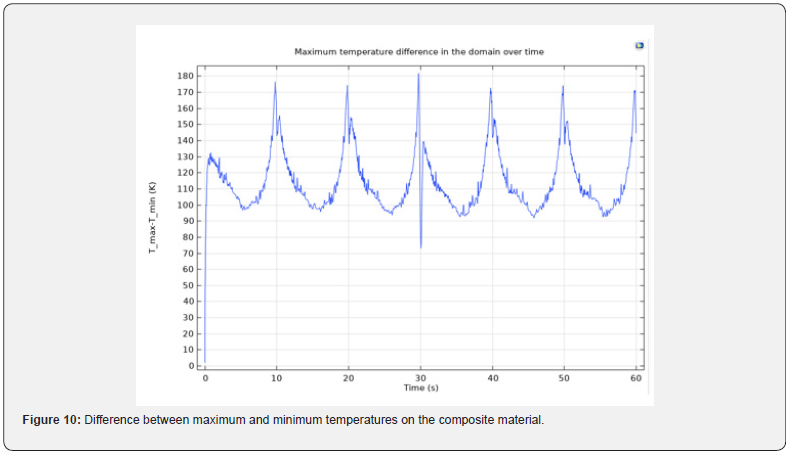
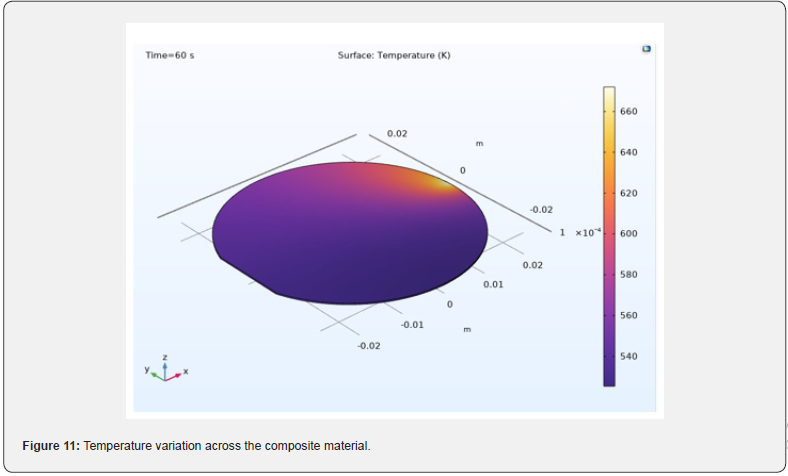
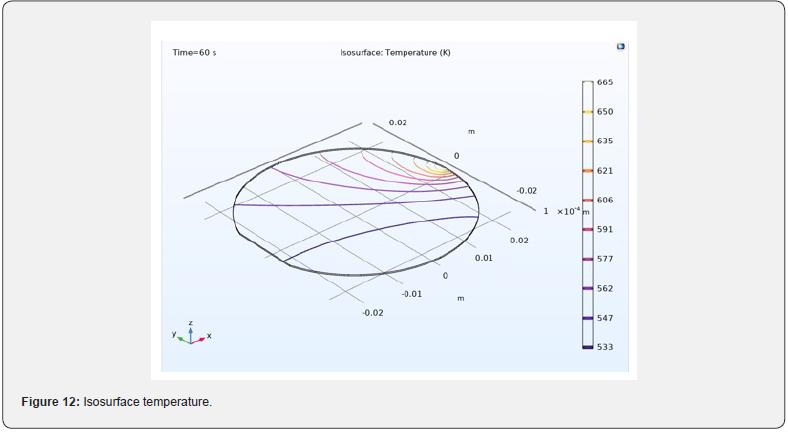
The heating profile does introduce some significant temperature variations, because the laser deposits the same amount of heat over a larger total swept area when it is focused on the outside of the composite material. An interesting modification to this example would be to investigate alternative heating profiles for smoother heating.

Conclusion

This paper simulates the mechanical and thermal performances of a designed and modeled material made up of Nomex (outer layer), Kevlar (supporting layer), and aerogel (core layer). First, this work demonstrates the modeling of a composite structure material made up of Nomex, Kevlar, and Aerogel materials. Three different methods are used to model the composite structure: Layerwise theory, Equivalent Single Layer (ESL) theory, and a multiple model method. Modal and frequencyresponse analyses are performed for the specified loading and the multiple model method is compared with the traditional layerwise and ESL theory in terms of performance and accuracy in the results, including through-thickness stress distribution. It is shown that the layerwise theory is accurate but computationally expensive. In contrast, the ESL theory is computationally less expensive but unable to capture the accuracy through thickness and the overall stress distribution. The multiple model method seems like the best choice in terms of accuracy and performance for modeling the composite structures.

After comparing the mechanical simulations results for different combinations performed in COMSOL, it appeared that the combination Nomex (outer layer), Kevlar (supporting layer), and Aerogel (core layer) is the best combination to be used as high-strength Composite Material for in-space Optical Mining Application.

Second, the material made up of Nomex, Kevlar, and Aerogel modeled and simulated to determine its strength (mechanical strength) is heated up by a laser that moves radially in and out over time, while the material itself rotates on its stage. Modeling the incident heat flux from the laser as a spatially distributed heat source on the surface, the transient thermal response of the material is obtained. The peak, average, and minimum temperatures during the heating process are computed, as well as the temperature variations across the material.

The thermodynamics simulation results showed that the material made up of Nomex/Kevlar/Aerogel is suitable to be used as a High-Temperature Resistant composite material for in-space optical mining applications. In sum, it appears from the mechanical and thermal performance simulations that the material made up of Nomex (outer layer), Kevlar (reinforcement layer), and Aerogel (core layer) is suitable to be used as high-strength and hightemperature resistant composite material for in-space optical mining applications (asteroid mining).

References

1. Brophy JR, Friedman L (2012) Returning an entire near-Earth asteroid in support of human exploration beyond low-Earth orbit,” IAF Global Exploration Conference, Washington, DC.
2. Tsuda Y, Yoshikawa M, Abe M, Minamino H, Nakazawa S (2013) System Design of the Hayabusa–2 Asteroid Sample Return Mission to 1999JU3. Acta Astronautica 91: 356-362.
3. Harris A, Barucci M, Cano J, Fitzsimmons A, Fulchignoni M, et al. (2013) The European Union Funded NEOSHIELD Project: A global Approach to Near-Earth Object Impact Threat Mitigation. Acta Astronautica 90(1): 80-84.
4. Singh L, Bortolami S, Page L (2010) Optimal guidance and thruster control in orbital approach and rendezvous for docking using model predictive control. AIAA Guidance, Navigation, and Control Conference and Exhibit, AIAA Paper 2010-7754, Toronto, Canada p. 1–15.
5. Holzinger M, DiMatteo J, Schwartz J, Milam M (2008) Passively safe receding horizon control for satellite proximity operations. 47^th IEEE Conference on Decision and Control, Cancun, Mexico pp. 3433-3440.
6. Di Cairano S, Park H, Kolmanovsky I (2012) Model Predictive Control Approach for Guidance of Spacecraft Ren- dezvous and Proximity Maneuvering. International Journal of Robust and Nonlinear Control 22(12): 1398-1427.
7. Reddy JN (2004) Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. Second Edition, CRC Press.
8. Grujicic M, Hariharan A, Pandurangan B, Yen CF, Cheeseman BA, et al. (2021) Fiber-Level Modeling of Dynamics Strength of Kevlar^® KM2 Ballistic Fabric. ASM International 21: 1107-1119.
9. Sharma P, Priyanka P, Mali HS, Dixit A (2020) Geometric modeling and finite element analysis of Kevlar monolithic and carbon-Kevlar hybrid woven fabric unit cell. Materials Today: Proceedings 26(2): 766-774.
10. Yadar MK, Kumar BB, Stephen DS, Vikas G, Swetha J (2022) Structural Analysis of Kevlar-49 Fiber Reinforcement Composite Material Using FEM. International Research Journal of Engineering and Technology (IRJET) 9(3).
11. Algahtani A (2016) Manufacturing of High Strength Kevlar Fibers.
12. Mather RR (2011) Chemistry of Textile Fibres. Chapter 6 High-Performance Fibres, Royal Society of Chemistry.
13. Paul M (2016) Kevlar, the super-tough fibre used to make bullet-proof vests, University of Bristol, UK.
14. Woodford C (2016) Kevlar.