Research Article

Room and Low-Temperature Ultrasonic Properties of Tellurite Glasses

Raouf El-Mallawany^1*, Amin Abd El Moniem² and M S Gafaar³

¹Department of Physics, Menoufia University, Egypt

²Department of Physics, Zagazig University, Egypt

³Department of Ultrasonic, National Institute of Standards, Egypt

Submitted: January 16, 2024; Published: January 29, 2024

*Corresponding author: Raouf El-Mallawany, Department of Physics, Menoufia University, Egypt

How to cite this article: Raouf El-Mallawany, Amin Abd El Moniem, M S Gafaar. Room and Low-Temperature Ultrasonic Properties of Tellurite Glasses. JOJ Material Sci. 2024; 8(3): 555737. DOI:10.19080/JOJMS.2024.08.555737

Abstract

The motivation of the present is to analyze theoretically room temperature bulk modulus and low-temperature ultrasonic attenuation coefficient in the glass system (1-x)TeO₂-xV₂O₅, x= 20, 25, 30, 35, 40 mol %. The bond compression (BC) and Makishima-Mackenzie (MM) models were used to interpret room-temperature bulk modulus. Correlation between room temperature bulk modulus and compositional parameters has also been achieved. The main parameters used were average cross-link density, number of network bonds per unit volume, and average atomic ring size. Analyses of low-temperature (300-150 K) ultrasonic attenuation at 2, 4, 5, and 6 MHz were achieved by calculating: potential energy, centers of energy loss, elongation, and contraction of the two-well potential. Also, the deformation potential is found to be sensitive to the variations of the modifier content. The analysis revealed a sensitive effect of variation of modifier contents for elongation or contraction of the dual-well potential. The number of centers of energy loss is related to the elastic moduli as a function of the modifier content.

Keywords: Glasses: Tellurite; Room Temperature; Elastic Moduli; Low Temperature; Ultrasonic Attenuation

Introduction

Advanced glass materials or ‘functional glasses’ are new glasses used for new technological purposes. New tellurite glasses containing transition metal oxides (TMO), or rare earth oxides (REO) have been prepared by the melt quenching technique and have an interesting physical property [1-14]. The elastic and other properties of glasses are of great importance. An extensive number of publications on the measurement of elastic properties of glasses, by using the ultrasonic non-destructive pulse-echo technique have been achieved [4,5]. The investigation of the elastic properties of glasses as a function of composition is very informative about the structure of glasses and they are directly related to the interatomic potentials [6,10, 11].

The objective of the present work is to analyze and correlate between room temperature elastic moduli [15] and low-temperature ultrasonic attenuation [16] for the semiconducting tellurite glasses in the form (1-x) TeO₂-xV₂O₅, where x = 20, 25, 30, 35, and 40 mole %.

Analysis and Discussions

Physical and Elastic Properties

Table 1 collected the selected room temperature values of density, molar volume, bulk modus, and Poisson's ratio of the investigated binary TeO₂-V₂O₅ glasses [15]. The molar volume was deduced from the density measurement and the chemical composition. A gradual decrease in density is observed as TeO₂ is replaced by V₂O₅. At first sight, the variation of density with composition is well understandable from the variation of density of the oxide constituents. The respective densities of TeO₂ and V₂O₅ are 5.670 and 3.357 g/cm³. The molar volume was found to be 31 cm³/mole for the base TeO₂ glass and increases from 33.48 cm³/mole in 80TeO₂–20V₂O₅ glass sample to 39.88 cm³/mole in 60TeO₂–40V₂O₅ glass sample. This may be due to the fact that the volume occupied by a V₂O₅ (54.18 cm³/mol) is larger than that of the TeO₂ (28.15 cm³/mol). In addition, the increase of V₂O₅ and expense of TeO₂ increases the oxygen ions in the glass network by a factor of 5/2, which increases the oxygen density from 4.679 x 1028 m^-3 in 80TeO₂–20V₂O₅ glass sample to 4.838 x 1028 m^-3 in 60TeO₂–40V₂O₅ glass sample (Table 1). The increase in the excess molar volume (where is the crystalline molar volume) supports this discussion and confirms the amorphous nature of the samples investigated.

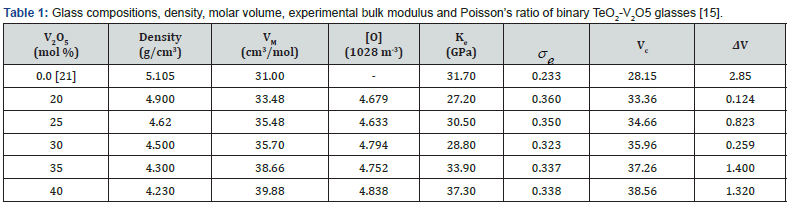
As density decreases, then there is an increase in glass molar volume, with a corresponding decrease in glass compactness or atomic packing density and elastic moduli. It has been proposed the following equation, which correlates experimental bulk modulus (K_e) with molar volume of the glass (V_M) [17,18],

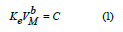
The constant C and power b have values depend strongly on the type of glass and its composition. The last equation suggests that a decrease in molar volume should lead to an increase in bulk modulus. Unfortunately, this is not true for the present TeO₂–V₂O₅ glasses. It is clear from Table 1 that the, by increasing vanadium oxide content from 20 to 40 mol%, the bulk modulus increased from 27.2 to 37.30 GPa and Poisson’s ratio decreased from 0.360 to 0.338. The relation between bulk modulus and molar volume reveals a forward proportionality as shown in figure 1. The least-square linear regressions performed on In K_e and V_M yields the following semi-empirical relationship,

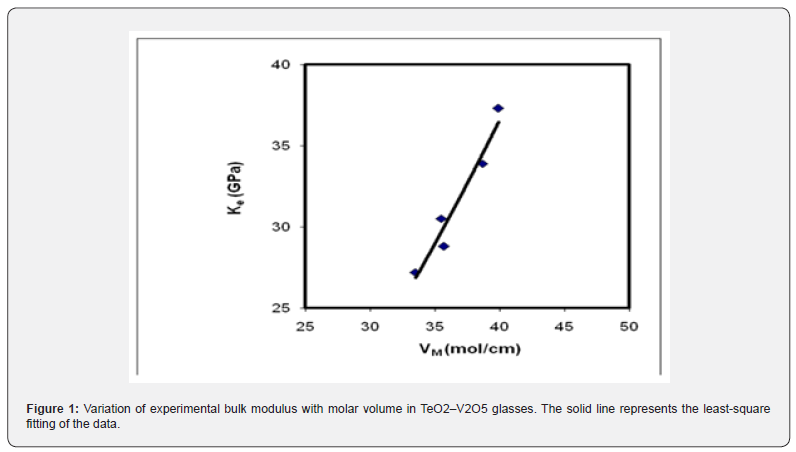
with R² = 0.946, b=-1.75 and C = 0.057. This suggests that the best fitting of the semi-empirical formula (7) to the data of these glasses was achieved at a negative value of b. These b and C values are completely different from those reported previously for V₂O₅–P₂O₅ glasses [19] or BaF₂–TeO₂ glasses [20]. In V₂O₅-contained tellurite glasses, vanadium ions can be found in either four-fold coordinated (VO₄ tetrahedron), or five-fold coordinated (VO₅ trigonal bipyramid) structural units [15,16,21,22]. Thus, the forward proportionality between molar volume and bulk modulus of TeO₂–V₂O₅ glasses may be associated with either, the network modification, or, the difference between the molar volumes of each component oxide. Previous ultrasonic and IR studies on pure tellurite and binary vanadium tellurite glasses [15,16,21,22] concluded that:

a) The network of pure TeO₂ glass is composed of TeO₄ tetragonal bipyramids and Te–O–Te linkages,

b) The addition of V₂O₅, beyond 20 mol% V₂O₅ in TeO₂–V₂O₅ glasses, changed the continuous tellurite network to continuous vanadate network. This resulted in the formation of VO₄ and VO₅ structural units in addition to TeO₄ tetragonal bipyramids and TeO₃ trigonal pyramids. Each VO₄ or VO₅ structural units has one V=O double bonds. These basic structural units are connected to each other through Te–O–Te, Te–O–V and V–O–V linkages.

c) The Te–O bonds (bond length = 1.98 Å) in TeO₂ are longer than V–O bonds (bond length = 1.83 Å) in V₂O₅ [15].

In the light of the above, the increase in bulk modulus with increasing V2O5 can be explained in two ways as follows:

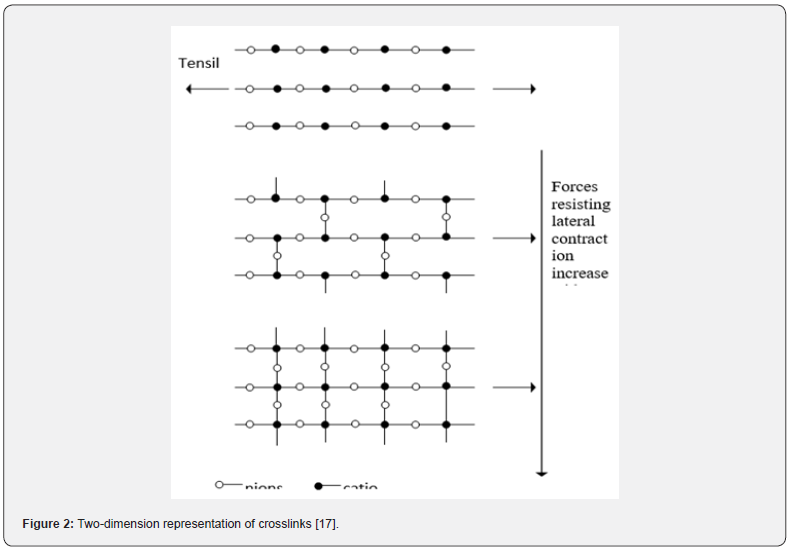
a) The formation of VO₄ and /or VO₅ structural units confirms the former role of vanadium ions. This is expected to close-packing and cross-linking the structure of the prepared TeO₂–V₂O₅ It has been found that, the substitution of TeO₂ by V₂O₅ from 20 to 40 mol % changed the average cross-link density from 2.33 to 2.57 [15] and the total packing density from 0.5639 to 0.5782 [23]. This stiffens the glass network as evidenced by the increase of the bulk modulus with increasing V₂O₅ content.

b) Each Te–O–V linkage is composed of Te–O and V–O bonds, which are considered to be two springs connected in series. Under a constant longitudinal stress, most of the longitudinal strain will appear in the weaker bond. According to our earlier studies, the first-order stretching force constants were 216 N/m for Te–O bonds and 277 N/m for V–O bonds [15]. This means that Te–O bonds are longer and weaker than V–O bonds [15, 22]. Consequently, under a constant longitudinal stress, most of the total longitudinal strain will appear in the weaker Te–O bonds. Thus, the addition of V₂O₅ and the expense of TeO₂ are expected to decrease the produced total strain. As a result the longitudinal modulus and consequently all other elastic moduli

Values for the theoretical bulk modulus (K_bc), Poisson’s ratio (σ_bc), and ring diameter (ℓ) were calculated according to the bond compression model and ring deformation models [24-27] by using the next relations:

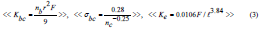
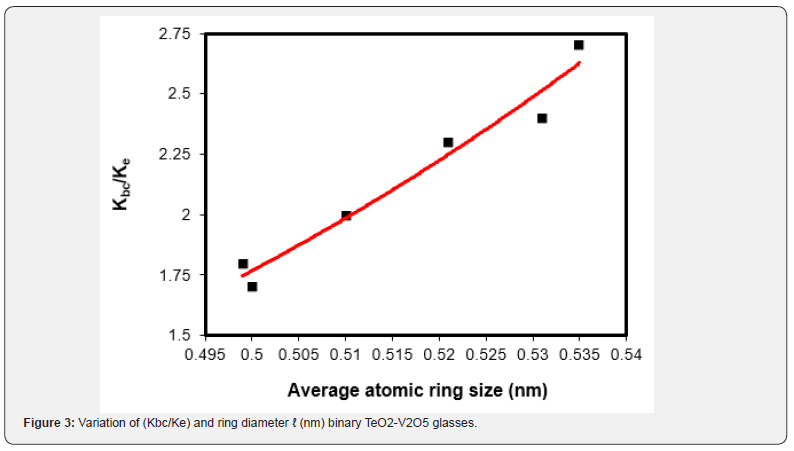
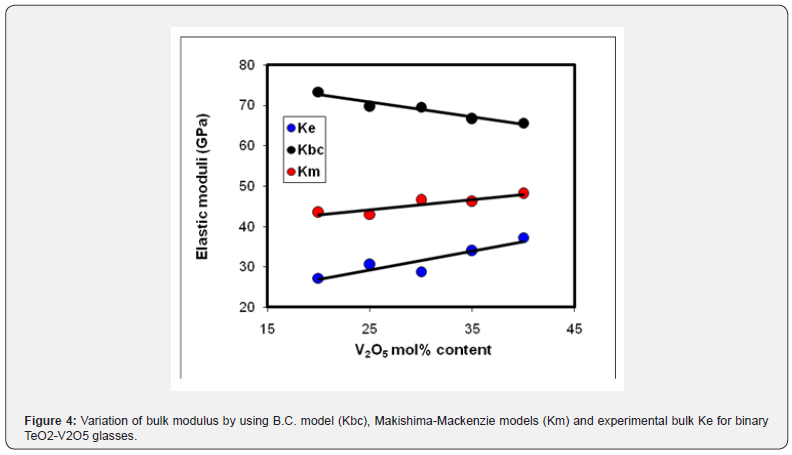
Where, n_b is the number of network bonds per unit volume, r is the cation-anion bond length =1.99 nm for TeO₂ and 0.183 nm for V₂O₅ [15,21], F is the average first-order stretching force constant = 216 N/m for TeO₂ and 277 N/m for V₂O₅, respectively [15,21], and is the average crosslink density. The calculated K_bc and σ_bc values are given in table 2. As can be seen from this table K_bc decreased from 73.3 to 65.6 GPa as the V₂O₅ increased from 20 to 40 mol%. These values are higher than the experimentally measured bulk modulus K_e. Also, the number of bonds per unit volume n_b decreased from 7.56 ×10²⁸ to 6.65×10²⁸ m^-3 in the same composition range. Theoretically, the decrease in the experimental Poisson’s ratio with an increase in V₂O₅ content is attributed to increasing the average cross-link density. The crosslink density is shown in figure 2. In the present case, the average crosslink density increased from 2.33 to 2.57. As a result, the calculated Poisson ratio σ_bc decreased from 0.227 to 0.221. Besides the above, the (K_bc) ratio decreased from 2.7 to 1.7. When (K_bc/K_e) is ≈ 1 this means that the interaction between neighboring bonds is neglected [24-27]. On the other hand, (K_bc/K_e) > 1 and less than 3, indicates a relatively open three-dimensional network [24]. Such conclusion of open three-dimensional network since the cross-link density values were found to increase indicates the change in the continuous tellurite network to continuous vanadate network with higher coordination number that will act to increase the average cross-link density. In the present case, all TeO₂-V₂O₅ glasses have (K_bc/K_e) values greater than 1, which are attributed to the open 3D structure [24-27]. The average atomic ring size ℓ values, which have been calculated from Eq.3, changed from 5.00 nm for pure TeO₂ glass [21] to 0.535 nm for 80TeO₂-20V₂O₅ glass sample and 0.499 nm for 40TeO₂-60V₂O₅ glass sample. The increase in (K_bc/K_e) ratio is attributed to the higher the atomic ring size ℓ (nm) as shown in figure 3. If the experimental bulk modulus K_bc<K_e, compression requires much less energy than that is that required for pure compression of network bonds.

Makishima-Mackenzie's model [28,29] was used for more interpretation of the elastic moduli according to the following equations:

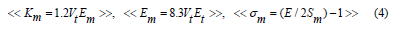
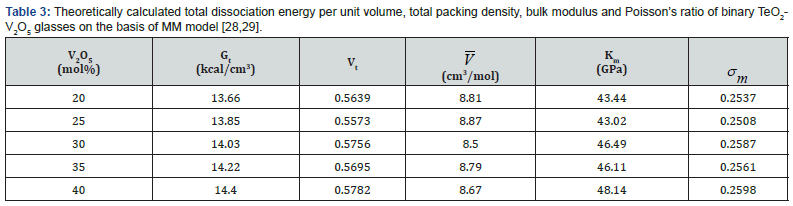
The packing density, V_t for the used oxides, TeO₂, V₂O₃; 14.7, 35.4 (cm³/mol) and dissociation energy, G_t; 54 and 69.5 (kJ/cm³) [30], respectively. The calculated elastic moduli according to (MM) are shown in table 3. Moreover, figure 4 shows the experimental bulk modulus, calculated bulk modulus according to the bond compression model and Makishima-Mackenzie's model. The calculated dissociation energy per unit volume Gt increased from 13.66 to 14.40 (kcal/cm³). Also, the mean atomic volume V decreased from 8.81 to 8.67 (cm³/mole). Moreover, both bulk modules K_m and Poisson’s ratio σ_m increased from 43.44 to 48.14 GPa and from 0.2537 to 0.2598, respectively.

Ultrasonic Attenuation

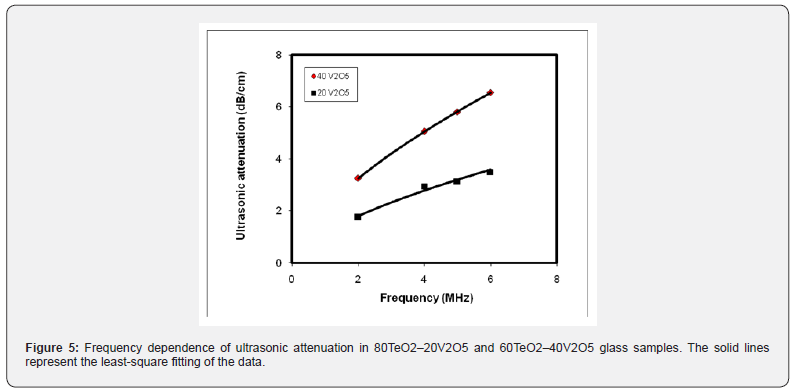
The frequency dependence of room temperature ultrasonic attenuation is shown in figure 5 for 80TeO₂–20V₂O₅ and 60TeO₂–40V₂O₅ glass samples. The increase in ultrasonic attenuation with increasing the frequency was fitted by a linear relation . This behavior is reasonable and agrees well with Abd El-Moneim's approaches [17,18,22].

The central force model [24-27] suggested oscillations of the light atoms in the glass structure in asymmetric two-well potential. These atoms are considered oxygen atoms. These atoms aim to surpass the wall elevation (activation energy). This aim is a result of the effect of ultrasonic energy on these atoms. The ultrasonic energy increases as the frequency (f) of these waves increase with the increment of the temperature as shown in table 4 and table 5. The increment of the ultrasonic energy formed extra oscillating oxygen atoms in a potential well. Therefore, the transmission of ultrasonic waves into the amorphous structure changes the equilibrium of the vibrating oxygen atom around the bottom of the well. This procedure created an energy change (ΔE) between the minima of the well. This energy shift can be presented by the deformation potential (D). The last parameter means the energy motion of the relaxing states in a strain field, so, it presents the interaction between ultrasonic waves within the asymmetric dual-well potential. The central force model [24-27] suggested an equation that represents the internal friction (Q^-1) of a set of oxygen atoms/volume (n) proceeding in comparable dual-well potential with a wall height E_h. When , the ultrasonic attenuation is maximum, and in this case, there is a distribution of both the activation energies and the relaxation times and will be

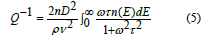
The oxygen atoms per unit volume (n) or the centers of energy loss can be taken as a summation of the probable activation energies as

The parameter n(E) can be described in terms of the ultrasonic velocity (v) the angular frequency (ω) and the density (ρ) [27] as

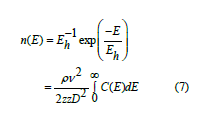
Where zz is a constant and the 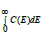is the total number of centers of energy loss. The last parameter can be deduced from α − T relation. The quantitative exploration of the central-force model [24-27] revealed that

There is a predictable oscillation of oxygen atoms well with atomic limits,

Such a well had single minima corresponds to the equilibrium of oscillated oxygen atoms,

These minima agree with small O oscillations. The minima will flatted at higher anharmonic oscillations,

The energy of the transmitted ultrasonic wave (longitudinal or shear) disfigured the well,

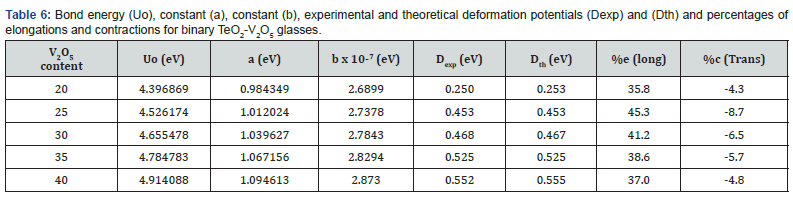
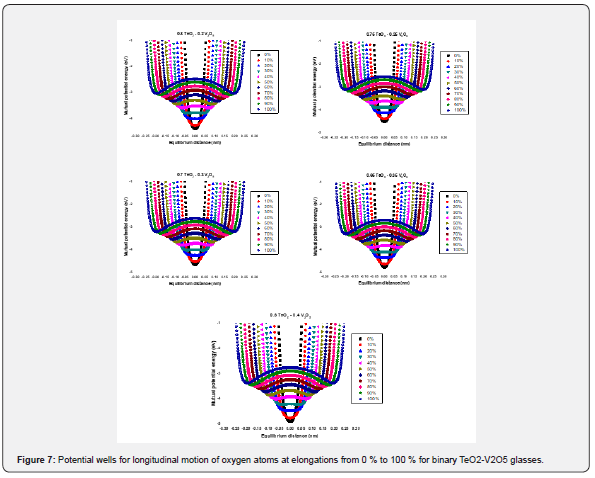
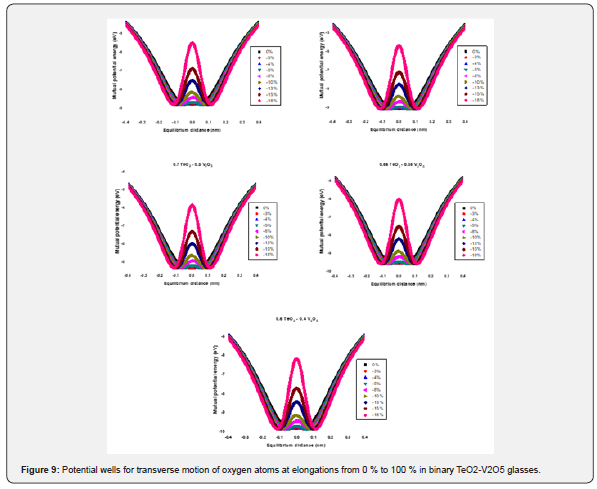
The well had a potential energy U and an elongation e based on the longitudinal or shear oscillations of O atoms as shown in the next equation,

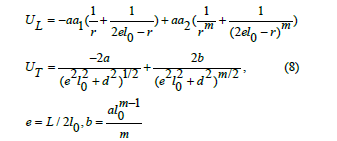
where aa₁ and aa₂ are constants, m takes values from 6-12, L is the cation-cation distance and l₀ expressed bond length in a definite glass structure. The term U/2 is a suitable expression for the potential energy U and in this case, characterized the alternate potential energy anion and cation (regarded as a heavier atom) as shown in figure 6.

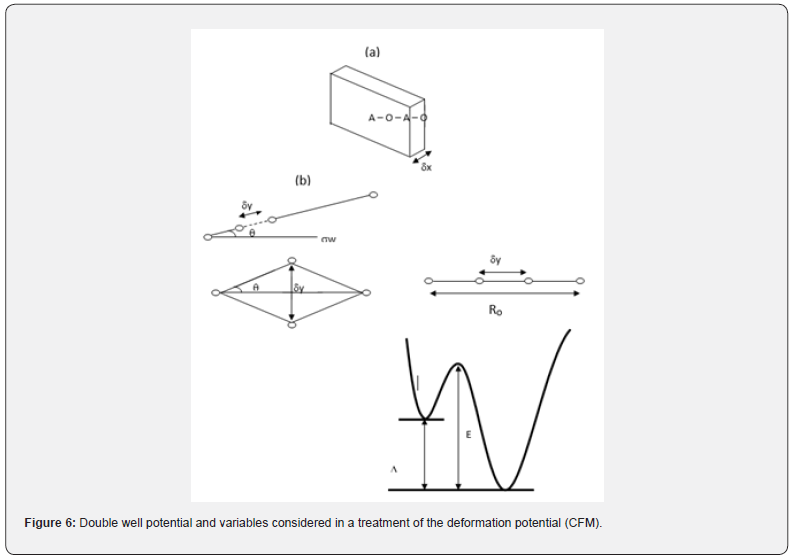
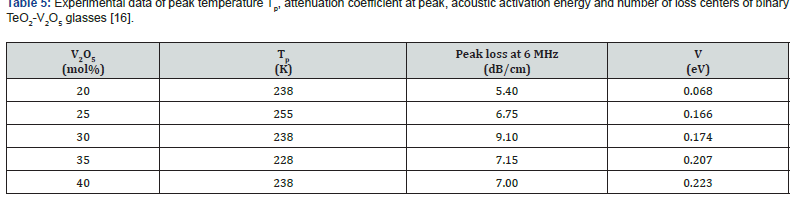
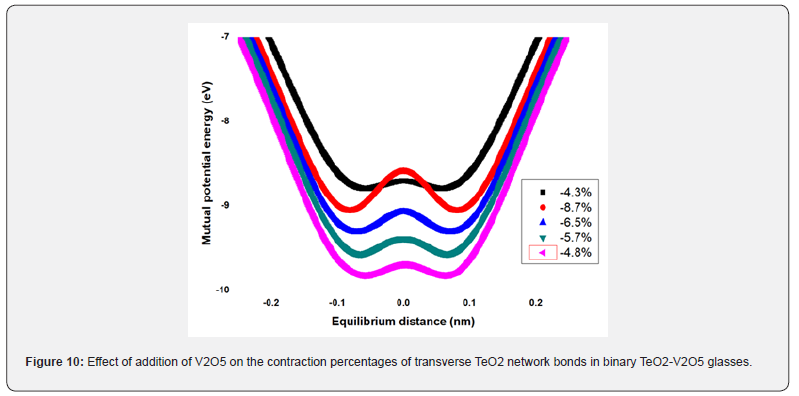
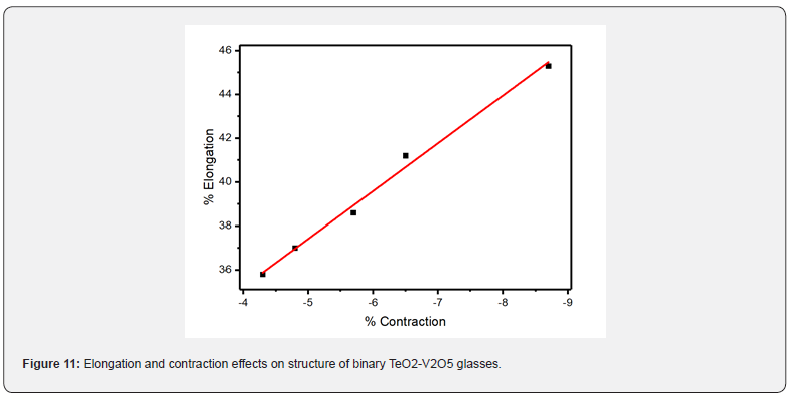
Low-temperature parameters are alternate potential energy, centers of energy loss, elongation, or contraction of the two-well potential. Moreover, the deformation potential is found to be sensitive to the variations of the modifier content. The number of centers of energy loss is related to the elastic moduli as a function of modifier content. Table 6 collected bond energy (U_o), constant (a), constant (b), experimental and theoretical deformation potentials (D_exp) and (D_th), and percentages of elongations and contractions of binary TeO₂-V₂O₅ glasses as shown in figures 7-10. It is clear that figure 11. showed an increase of percentage longitudinal elongations with the increase in percentage transverse contractions, which means that the glass network structure increased horizontally in longitudinal chains and decreased vertically in transverse chains, confirming the increase in the dimensions of the 3D network structure and consequently the increase in molar volume.

Conclusion

The increment of V₂O₅ structural units in the tellurite network is congruent with the increment of the number of centers of energy loss increases, the acoustic activation energy increases, and a dual-well potential will be formed as a direct result of the oscillations of oxygen atoms. The oscillations are created from the effect of ultrasonic energy, the created potential well suffers from some changes as the supposed ultrasonic energy increases. The potential well changes from an equilibrium state to a flat-bottom state to a dual-well potential, the last well corresponds well to the ultrasonic activation energy within the elastic limits, and besides that and more ultrasonic energy effect on the oxygen atoms will change the elasticity of the well and it will be no longer matching the proper activation energies. So, the well will be wracked. The increment of the bulk modulus as a function of V₂O₅ increased the deformation potential of the presented dual-well state. The impact of the present findings indicates that V₂O₅ didn’t act to fill the interstices and was added to the longitudinal chains, confirming the increase in molar volume with the increase in V₂O₅ content, and consequently the structure becomes more open with V₂O₅ content.

Credit Authorship Contribution Statement

R El-Mallawany: Idea, data curation, methodology, validation, investigation, writing original draft. Amin Abdel Moniem, and M S.Gafaar: data curation, methodology, calculations and shared in the analysis. All authors provided critical feedback and helped shape the research, analysis, and manuscript.

Prime Novel Statement

 All authors agree with this final version of the MS and also declare it was not submitted or published in other journals nor any other kind of publication. The authors declare that there is no financial interest in this work.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. Awshah A, Nazrin SN, Halimah MK, Effendy N, Khaliq MASMS, et al. (2023) Novel of neodymium nanoparticles zinc tellurite glasses in experimental and theoretical elastic properties using artificial intelligence approach. Chinese Journal of Physics 81: 332-353.
2. D Souza AN, Padasale B, Murari MS, Karunakara N, Sayyed MI, et al. (2023) TeO₂ for enhancing structural, mechanical, optical, gamma and neutron radiation shielding performance of bismuth borosilicate glasses. Materials Chemistry and Physics 293: 126657.
3. El Mallawany R, Gaafar MS, Azzam YA (2014) Prediction of ultrasonic parameters at low temperatures for tellurite glasses using ANN. Chalcogenide Letters 11(5): 227-232.
4. El Mallawany R, Abousehly A, El Rahamani AA, Yousef E (1998) Radiation effect on the ultrasonic attenuation and internal friction of tellurite glasses. Materials chemistry and physics 52(2): 161-165.
5. Elkhoshkhany N, El Mallawany R, Syala E (2016) Mechanical and thermal properties of TeO₂–Bi₂O₃–V₂O₅–Na₂O–TiO₂ glass system. Ceramics International 42(16): 19218-19224.
6. El Adawy A, El Mallawany R (1996) Elastic modulus of tellurite glasses. Journal of materials science letters 15(23): 2065-2067.
7. El Mallawany RA, El Deen LMS, Elkholy MM (1996) Dielectric properties and polarizability of molybdenum tellurite glasses. Journal of materials science 31(23): 6339-6343.
8. El Zaidia MM, Ammar AA, El Mallwany RA (1985) Infra‐Red Spectra, Electron Spin Resonance Spectra, and Density of (TeO₂)100−x–(WO₃)x and (TeO₂)100−x–(ZnCl₂)x Glasses. physica status solidi (a) 91(2): 637-642.
9. El Mallawany R, Gaafar MS, Veeraiah N (2015) Evaluation of Bulk Modulus and Ring Diameter of Some Tellurite Glass Systems. Chalcogenide Letters 12(2).
10. El Mallawany R (1993) Longitudinal elastic constants of tellurite glasses. Journal of applied physics 73(10): 4878-4880.
11. El Mallawany A, Saunders GA (1988) Elastic properties of binary, ternary and quaternary rare earth tellurite glasses. Journal of materials science letters 7(8): 870-874.
12. Kamalam EB, Manikandan N (2023) Review - Recent Advances in Bismuth Tellurite Glasses for Photonic and Radiation Shielding Applications. ECS Journal of Solid State Science and Technology 12(7): 076007.
13. Sidkey MA, El Mallawany RA, Abousehly AA, Saddeek YB (2002) Relaxation of longitudinal ultrasonic waves in some tellurite glasses. Materials chemistry and physics 74(2): 222-229.
14. Hampton RN, Hong W, Saunders G, El Mallawany RA (1988) Dielectric properties of tellurite glass. Physics and chemistry of glasses 29(3): 100-105.
15. Sidkey M, El Mallawany R, Nakhla RI, Abd El Moneim (1997) A Ultrasonic studies of (TeO₂) 1-x-(V₂O₅) x glasses. Journal of non-crystalline solids 215(1): 75-82.
16. Sidkey M, El Mallawany R, Nakhla RI, Abd El Moneim (1997) A Ultrasonic attenuation at low temperature of TeO₂–V₂O₅ Physica status solidi (a) 159(2): 397-404.
17. Gopal E, Mukundan TS, Philip J, Sathish S (1987) Low temperature elastic behaviour of As-Sb-Se and Ge-Sb-Se glasses. Pramana 28: 471-482.
18. Rajendran V, Palanivelu N, Modak DK, Chaudhuri BK (2000) Ultrasonic investigation on ferroelectric BaTiO₃ Doped 80V₂O₅-20PbO oxide glasses. physica status solidi (a) 180(2): 467-477.
19. El Moneim AA (2017) Theoretical analysis for ultrasonic properties of vanadate-phosphate glasses over an extended range of composition: Part II. Journal of Non-Crystalline Solids 465: 49-54.
20. El Moneim AA (2018) BaF₂–contained tellurite glasses: Quantitative analysis and prediction of elastic properties and ultrasonic attenuation–Part I. Journal of Fluorine Chemistry 212: 156-165.
21. Lambson EF, Saunders GA, Bridge B, El Mallawany RA (1984) The elastic behaviour of TeO₂ glass under uniaxial and hydrostatic pressure. Journal of non-crystalline solids 69(1): 117-133.
22. El Moneim AA (2002) DTA and IR absorption spectra of vanadium tellurite glasses. Materials Chemistry and Physics 73(2-3): 318-322.
23. El Moneim AA, Alfifi HY (2018) Approach to dissociation energy and elastic properties of vanadate and V₂O₅-contained glasses from single bond strength: Part I. Materials Chemistry and Physics 207: 271-281.
24. Bridge B, Patel ND, Waters DN (1983) On the elastic constants and structure of the pure inorganic oxide glasses. physica status solidi (a) 77(2): 655-668.
25. Bridge B, Higazy AA (1987) Prediction of low-temperature ultrasonic relaxation phenomena in oxide glasses from elastic properties. Journal of materials science letters 6: 1007-1012.
26. Bridge B, Patel ND (1986) Correlations between low-temperature ultrasonic relaxation parameters and other physical properties for the oxide glasses. Journal of materials science letters 5: 1255-1257.
27. Bridge B, Higazy AA (1988) Ultrasonic relaxation in CoO-P₂O₅ glasses at high temperatures. Journal of materials science 23: 438-450.
28. Makishima A, Mackenzie JD (1973) Direct calculation of Young's moidulus of glass. Journal of Non-Crystalline Solids 12(1): 35-45.
29. Makishima A, Mackenzie JD (1975) Calculation of bulk modulus, shear modulus and Poisson's ratio of glass. Journal of Non-crystalline solids 17(2): 147-157.
30. Inaba S, Oda S, Morinaga K (2003) Heat capacity of oxide glasses at high temperature region. J. Non-Cryst. Solids 325(1-3): 258-266.