Review Article

To the Question of Intensification of the Process of Grinding Materials in Drum Mills

Chizhik E F*, Khablo G P and Gerasimenko I I

Limited Liability Company, Research and Production Enterprise Mekhanobr-Polymet, Ukraine

Submitted: July 30, 2022; Published: September 30, 2022

*Corresponding author: Chizhik E F, Limited Liability Company, Research and Production Enterprise Mekhanobr-Polymet, Ukraine

How to cite this article: Chizhik E F, Khablo G P, Gerasimenko I I. To the Question of Intensification of the Process of Grinding Materials in Drum Mills. JOJ Material Sci. 2022; 7(2): 555707. DOI:10.19080/JOJMS.2022.07.555707

Abstract

The possibility of intensifying the process of destruction of ores in drum mills due to a change in the dynamics of the movement of the intra-mill medium when using the elastic properties of rubber as a structural material is theoretically substantiated. Design solutions for the profile of linings for mills are presented, which provide an increase in service life and improvement in technological performance.

Keywords: Rubber lining; Ore grinding mill; Fluid motion dynamics

Review Article

The theoretical mode of operation (the movement of the intramill load) in drum mills is divided into cascade, waterfall and mixed - cascade waterfall. It is necessary to highlight the last two as the most common in ball mills and self-grinding mills [1].

Technological loading (grinding bodies and crushed material) is entrained in movement along arc trajectories by friction forces between the lining of the mill drum and the layers of loading adjacent to it. Due to friction between adjacent layers, the load is set in motion. If the friction forces between the layers are insufficient, then moving along arc trajectories, they can slip relative to each other. There will be no slippage of the technological load on the surface of the lining when the moment of its friction force relative to the mill axis will balance the moment of the tangential components of gravity relative to the same axis.

The elementary mass of the layer moves along arc trajectories, from the lower position to the upper one, entrained in motion by friction forces and due to the support of the lower part of the material of the same layer. In the upper part of the mill drum, as soon as the component of the reaction of the lining normal to the surface of the lining to the elementary mass of the loading layer turns to zero, it breaks off and goes into free flight along a parabolic trajectory. When the elementary mass meets the lining or the upper layer of the load located on the mill drum, an impact occurs, as a result of which the lining will experience additional pressure in addition to the pressure from gravity and the centrifugal force of inertia of the load. In addition, in the central part of the intra-mill load there will be a slow-moving core, which is a segment-shaped form. It is called slow-moving because inside it the technological load, which is in the motion mode, moves much more slowly than the material located on arc trajectories. In a sedentary core, the destruction of the material occurs due to its abrasion due to the sliding of the layers relative to each other.

The efficiency of grinding mills largely depends on the design of the lining, the correct choice of geometric parameters and mechanical characteristics of lining coatings, as well as the speed of rotation of the drum mill [2,3]. In addition, it is possible to achieve an increase in the abrasion of the crushed material by increasing the relative vertical movement of the layers of the technological load. The latter is achieved due to the presence of metal inserts on the working surface of the rubber lining of the mill. Figure 1a shows that on the shell 1 of the mill drum there is a rubber lining 2 with a thickness a p, in which metal inserts 3 with a width a m and a height h m are vulcanized with a step a p with a thickness of the rubber layer under them (h_p - h_m). Thanks to this constructive solution, different relative vertical motion of the medium layers located on the rubber and metal inserts is achieved.

Let’s build a simplified mathematical model of the technological environment with its vertical oscillations at the initial speed V₀ (Figure 1b). The medium is considered as a regular system of adjacent vertical layers above metal inserts of mass c_m, connected to the drum shell by means of elastic bonds with reduced stiffness c_rm, and layers above the rubber, connected to the shell by elastic bonds with reduced stiffness c_pr.

In this case, we will assume that for the technological load under consideration, the layers above the metal insert and the layers above the rubber are not compressible and they move in the vertical direction relative to each other. Neighboring layers are pressed against each other, experiencing lateral pressure q_x(z) (z is the coordinate of the cross section of the medium layer). In addition, we will assume that the vertical pressure q_z(z)and lateral q_x(z) pressures and q_y(z) obey Pascal’s law for an ideal fluid, i.e.

Due to the relative movement of the layers in the vertical direction, tangential pressures will act between them along the side surfaces τ(z) due to the presence of sliding friction forces

where f is the coefficient of sliding friction.

T

This approach is justified if the propagation velocity of a This approach is justified if the propagation velocity of a longitudinal sound wave in a medium (E - reduced modulus of elasticity of the first kind for the technological environment is the reduced density of the medium) will be significantly higher than the speed of vertical movement of the layer supported from below by an elastic bond with the reduced stiffness of rubber c_pr underneath the material.

This approach is justified if the propagation velocity of a The vertical pressure of the layer is determined by the force of gravity of the technological load over the section z (Figure 2).

Consider an elementary layer of material dz located between cross sections z and z + dz . Under the action of gravity forces dG = ρ gFdz , vertical pressure forces q_z (z)F and −q_z (z)F , lateral forces q_x (z) pdz , q_y (z) pdz (F and p are, respectively, the area and perimeter of the cross section of the layer) and −q_x (z) pdz , −q_y (z) pdz , as well as lateral tangential forces, the τ (z) pdz elementary layer will be in equilibrium, i.e. in projections onto the z -axis, we get

( dT − elementary tangential force ) Then the total gravity G and tangential force T will

Since the relationship is q_z (z) linear, then

Substituting expression (5) into (4), we obtain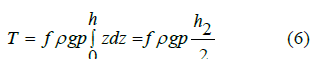

Let us write the equation of vertical motion of the mass of the M = ρ FH technological load layer under the action of gravity G = ρ gFH , tangential force 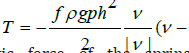relative speed of the layer), elastic force of the spring vertical displacement of the medium layer)

The last equation can be rewritten as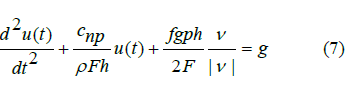

To equation (7) it is necessary to add the initial conditions

Nonlinear equation (7) is solved as follows. Let us first consider the first stage, when ν / |ν |= 1 , i.e.

The solution of the linear inhomogeneous equation of the second order (9) is found as the sum of the general solution of the homogeneous equation

frequency of natural oscillations) and a particular solution of the u(t) inhomogeneous equation (9) [4]

Then the general solution of equation (9)

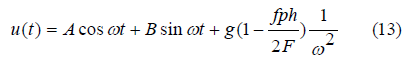
We find the integration constants A and B from the initial conditions (8). From the condition u(0) = 0 we obtain

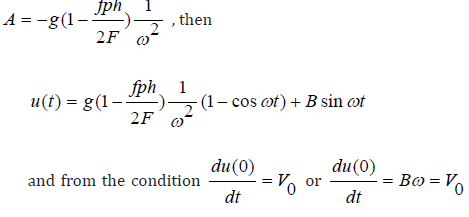
Let’s introduce the following notation: u_p(t) − movement of the vertical layer of the technological medium over the rubber, and u_M(t) − movement of the layer over the metal insert. Then the displacements u_p(t) and u_M(t) , as well as their absolute velocities V_p(t) and V_M(t) will be in accordance with formulas (14) and (15), i.e.

The speed of the layer over the rubber relative to the speed of the layer over the metal insert

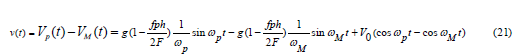
Solution (16)-(19) is valid as long as the velocity of the v(t) relative motion of the layers remains a positive value, i.e. for time t ∈[0, t₁) , where t₁ is the moment of time corresponding to zero speed v(t) . The value t = t₁ is found from the condition

The solution t = t₁ of the transcendental equation (22) can be obtained by one of the approximate numerical methods. Then we find the initial values for solutions u_p(t) and u_M(t) , as well as for their absolute velocitiesV_p(t) and V_M(t) based on expressions (16)-(19).

Then the solution of the stated problem for t ∈[t₁, t₁) is found on the basis of the solution of the system of equations (23) taking into account that v(t) < 0 or v(t)/ | v(t) |= −1

Integration constants A_r, B_{rv, Am, Bm are found based on the solution of the system of equations (23) taking into account relations (24), i.e. systems of equations}

Here, the right parts of system (25) are found on the basis of expressions (16)-(19), i.e.

Then the solution of the system of linear equations (25) will be

Time t = t₂ corresponding to the end of the second stage, we find from the condition that the relative speed v(t₂) = 0 , i.e.

This equation , as well as equation (22) is solved by one of the approximate numerical methods.

Continuing the process of obtaining a solution using the above method, you can find a solution to the problem for any number of cycles. Let us consider another case, when the technological load can be represented as alternating vertical layers over the rubber a_p×1×h (Figure 3) and a_m×1×h over the metal, moving horizontally with an initial speed V₀^g.

Proceeding similarly to the previous case, we will find equations describing the horizontal displacements of adjacent layers relative to each other, i.e. the layer above the rubber relative to the layer above the metal insert, and vice versa [5].

Let us denote the horizontal displacements over the rubber w_p(z) as, and over the metal insert as w_M(z) . The intensity of horizontal tangential forces acting on the side surfaces of adjacent layers is defined as

where f is the coefficient of sliding friction of the layers relative to each other.

The intensity of the horizontal tangential forces acting on the layer from the side of the base are found by the formula

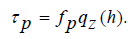
Here f_p − is the sliding friction coefficient of the layer over the rubber

Similarly , there 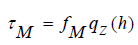is

where f_M − is the sliding friction coefficient of the layer over the metal.

Thus, the equations for the horizontal motion of the layers over the metal and over the rubber will have the form

Here, the relative horizontal velocity of the layers

and horizontal speeds over the metal insert 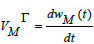and over the rubber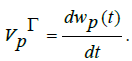

The initial conditions of problem (30)-(31) will have the form

Consider the first stage of the solution, when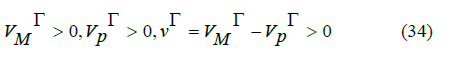

In this case and

And equations (30)-(31) will take the form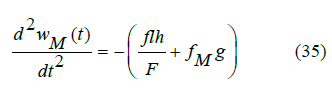

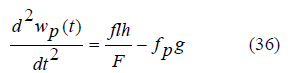
and their solution, taking into account the initial conditions (33), will be

Sliding layers on metal and rubber occurs until and , i.e. bye

The given theoretical mechanism of interaction of the intramill medium is valid for a short time interval of the steady-state mode of motion. In fact, the constancy of the mode of motion (cascade, waterfall, mixed) does not exist. Confirmation of this conclusion is the wear of the back side of the teeth of the drive gear and the crown of the drum, since the speed of its rotation changes upwards. Intra-mill loading will necessarily be located in the area of the angle of repose (self-collapse), there will be an instantaneous movement of the medium to the side of the drum opposite to the direction of rotation. This will lead to an acceleration of rotation due to a change in the center of gravity. The change in the noise level (acoustic changes) is also a confirmation of the lack of constancy of the mode of motion of the medium. In the submarine fleet there is a profession - acoustics. The most convincing to confirm our conclusions - the lack of constancy of the mode of movement, is a change in the current load. The ammeter needle deviates from the average position both to the right and to the left, i.e. there is an increase and decrease in the load in a fairly short time interval.

The use of the unique property of rubber - elasticity allows you to create designs of rubber linings that help intensify the process of grinding (separating) ores. The most promising are designs with a wave profile at different heights and wavelengths, which significantly change the dynamics of the movement of the intra-mill environment. Also, wave structures with an internal closed air cavity and magnetic ones, which form a wave due to the constructive - magnetic accumulation of scrap (worn balls), have also positively proven themselves.

The given design solutions create conditions for increasing the dynamics of the interaction of the environment, theoretically presented by us in this article. In general, along with an increase in the overhaul period, wave rubber linings provide an opportunity for a significant improvement in technological performance to reduce the consumption of balls and electricity; increase in productivity in terms of feed and finished class, when operating mills with a reduced diameter and a total mass loading of balls; reduce noise and harmful low-frequency vibration.

References

1. Kryukov DK (1966) Improvement of grinding equipment of enrichment enterprises. M Nedra, pp. 176.
2. Tarasenko AA, Korotkikh BI, Real VA, et al. (1982) On the possibility of using elastomers for lining ore-pulverizing mills of the first stage of grinding. Mining and processing of non-ferrous metal ores. Norilsk pp. 92-96.
3. (1985) Protective linings and coatings for mining and processing equipment. In: Tarasenko AA, Chizhik EF, Vzorov AA, et al. (Eds.), pp. 204.
4. Timoshenko SP (1967) Fluctuations in engineering. M Nauka, pp. 444.
5. Chizhik EF (2005) Drum ore grinding mills with rubber lining. Barnaul, pp. 360.