Journal Material Science | Open Access Publishers

Review Article

Contact Multiphysics: A New SPS Paradigm to Enhance Material Fabrication by Design

Giovanni Maizza*

Department of Applied Science and Technology, Politecnico di Torino, Corso Duca degli Abruzzi, Italy

Submission: December 05, 2017; Published: December 13, 2017

*Corresponding author: Giovanni Maizza, Department of Applied Science and Technology, Politecnico di Torino, INSTM, Unità del Politecnico di Torino, Via G. Giusti, 9 - 10121 Firenze, Corso Duca degli Abruzzi, 24 - 10129 Turin, Italy.

How to cite this article: G. Maizza. Contact Multiphysics: A New SPS Paradigm to Enhance Material Fabrication by Design. JOJ Material Sci. 2017; 3(3): 555615. DOI:10.19080/JOJMS.2017.03.555615

Abstract

Spark Plasma Sintering (SPS) is used extensively to fabricate a wide range of monolithic and advanced materials over a short time and at low temperatures which show inherent advantages over conventional hot-pressed materials. However, the presence of uncontrolled microstructure inhomogeneities, especially in relatively large SPS samples, greatly limits the successful transfer of this technology to an industrial process. The intricate complexity of the involved SPS phenomena, the nebulous role of contacts and the tight physical coupling between the powder and the device are the main concerns. This work has three aims: a) to introduce the concept of contact multiphysics in SPS: b) to illustrate that the current issues can be framed within the unifying concept of contact multiphysics: c) to point out that an in-depth understanding of contact multiphysics will contribute significantly to the shedding of the light on SPS phenomena, in order to solve the current limitations of SPS technology and to enable the desired SPS fabrication of materials by design.

Introduction

Spark plasma sintering is an ECAS technology [1] in which an initial powder mixture, in the form of loose powder or green compact, undergoes interparticle bonding and subsequent densification upon application of a mechanical pressure and the simultaneous presence of electrical and thermal fields. The two key process parameters are pressure and voltage drop or current strength. The influence of these two parameters on densification and final properties has been the subject of many studies on both conductive and insulating materials. The primary purpose of electric currents in conducting particulate materials is to provide the required resistive heating [1,2]. However, it has been claimed that additional electric-factors, such as the removal of surface oxide, electromigration, and electroplasticity may enhance powder sintering through the activation of one or more concurring mechanisms [1].

In SPS, the electric currents are driven from two outer electrodes to the inner powder and its confining die through two stacks of cylindrical graphite elements (e.g., rams, spacers, punches) which are placed above (upper stack) and below (lower stack) the powder. The contacts between the graphite elements in both stacks become alternate preferential sites of electrothermal phenomena whenever crossed by a current. According to Holm’s law, the overall contact resistance between two contacting surfaces includes two contributions, namely a constriction resistance and a film resistance. The former is proportional to the electrical resistivity of both contacting materials and inversely proportional to the number and diameter of the a-spots (n . a). The latter is proportional to the electrical resistance of the interposed insulating film and inversely proportional to the contact area Ac. The upper and lower stacks are geometrically symmetric about a horizontal plane that passes through the powder core. The diameter of the rams and spacers generally decrease from the outer electrodes to the powder which inevitably originate a series of horizontal macro-contact interfaces (hereinafter, macrocontacts) but also a number of macro-constrictions [3].

Macro-constrictions can be distinguished between direct and reversed ones. When the former is crossed by currents, the field lines tend to concentrate, and these results in a higher local temperature at the contact interface. Conversely, in the latter, the field lines tend to spread over a larger region, thereby mitigating the thermal effects at the contact interface. Note that, for the purpose of this work, the mode of supplying the currents (either DC or pulsed DC and either temperature control mode or current control mode) is irrelevant. Myriads of interparticle contacts also exist in a powder. Pure metallic powders, when crossed by a current, dissipate heat mainly by constriction effect [3] as the volume of particles is relatively insignificant compared to their surfaces. If the interparticle contacts entrap some insulating films (e.g., oxides, grease, dust) of specified effective thickness [3] an additional contact resistance adds up. Dielectric films, interposed between conducting particles, can breakdown during SPS in pulsed DC [4] or rapid continuous DC [2] heating. Although film effects could in principle exist in both micro- and macrocontacts the presence of graphite in the tools make this circumstance less likely due to graphite chemical inertness even at elevated temperature. When currents cross a constriction region or a contact film, regardless their dimensional scale a voltage drop and a temperature jump are determined as a result of Joule heat dissipation. On the other hand, contact surfaces exhibit higher energy and are intrinsically more reactive than bulk regions since surface atoms are less tightly bound than bulk atoms.

die interfaces require special consideration, as many discrete micro-surfaces of particles are in contact with a continuous surface. These special contact interfaces are responsible for the intricate micro-macro electrothermal coupling that takes place between the powder and the SPS device tools. The integral of such micro-contact areas increases as the powder shrinkage increases. Any contact interface of the SPS system may in general undergo electric, thermal, displacement, chemical reactions and other kinetic phenomena which determine the innate contact multiphysics nature of a SPS system. At particle scale, the contact multiphysics may be enhanced by straining of the particles by the intrinsic reactivity of their surfaces (Figure 1).

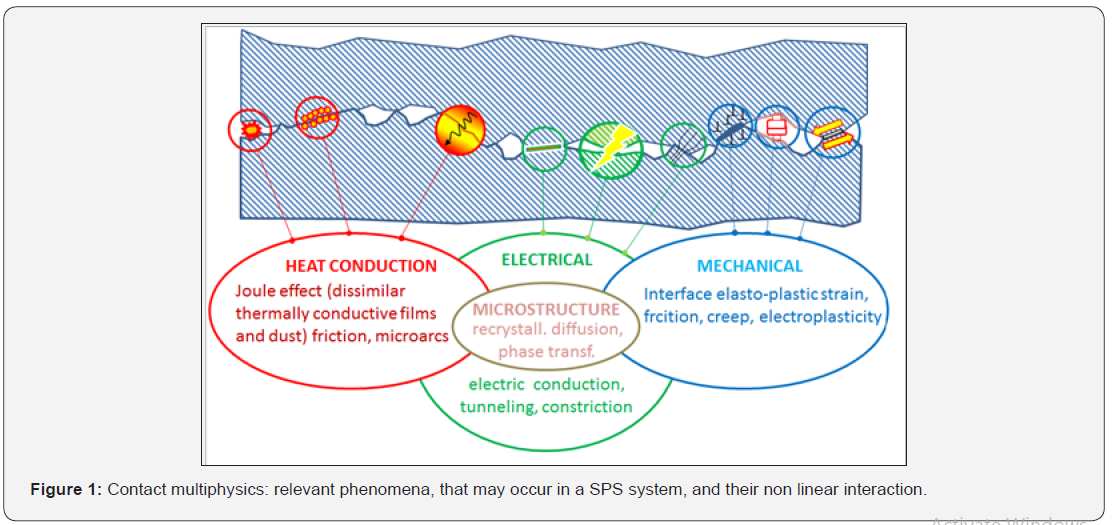
Contact Phenomena in SPS Devices

The most common SPS devices investigated throughout the world are the Syntex (or Sumitomo, Japan) [5-11] and the FCT (Systeme GmBH, Germany) [12-15]. Both systems share various similar geometric, functional and control features, the most relevant being the tool working concept and tool geometry. An upper and a lower stack of graphite elements are responsible for transmitting pressure and driving the currents toward the powder. Both stacks exhibit a series of horizontal and vertical contact interfaces (hereinafter, macrocontacts). Such interfaces operate in the SPS device as formidable electrical (and thermal) resistances which combine a regular contact resistance (due to rough contacting surfaces and the presence of an insulating film, if any) and additional macroconstrictions, due the difference in diameter of the contacting graphite elements. The latter resistances have a relevant effect on the SPS phenomena. Horizontal macroconstrictions can be found at the electrode/ ram and ram/spacer, spacer/spacer interfaces. A special macroconstriction is located at the vertical punch/die interface since it is reversed other than a sliding contact. Consequently, it leads to significant changes in electric and thermal fields during SPS. As the relative contact area increases with increasing time (i.e. shrinkage). such macroconstriction is responsible of diverting the electrical and thermal between fields the punches and the die. It is worth noting that, constriction phenomena are naturally accounted for by the finite element.

The crucial importance of contact resistances in SPS devices can be appreciated by analyzing the work of Wang et al [16]. The authors state that their three-way SPS model does not include the effect of contact resistances. They show that their model can capture the essential multiphysics of SPS phenomena, including the residual stress effects. However, the authors recognize that the predicted temperatures and temperature gradients are too low at steady state in both alumina and copper (solid) samples. However, it must be clarified that this model, in fact, it does consider the marked contribution of SPS contacts related with macroconstrictions being the major contribution in their SPS device. They evaluated macroconstriction effects along with their finite element solution by solving the Laplace’s equations. They only assumed, however, that all contacting surfaces were ideal. Such assumptions may be fair for a qualitative solution but insufficient for a quantitative prediction. Indeed the major source of error affecting SPS models is given by the neglect of the vertical contact resistance especially during shrinkage. On the other hand, the film resistance contribution can be reasonably neglected provided that the contacting surfaces are not excessively damaged or contaminated.

Prior estimation of contact resistances is a fundamental step of a SPS model before being reliably used to optimize a material or process. Horizontal and vertical contact resistances are tightly coupled, both electrically and thermally. One way to separate them is to replace the powder with a solid compact [16-18], or solid graphite [7,19,20] or to omit the sample [13]. Horizontal contact resistances are generally less important than vertical contact resistances but exhibit a more complex behavior [13]. Horizontal contact resistances account for the electric and thermal resistances of contacting graphite elements and powder along the axial direction. Conversely, the vertical contact resistances act along the radial direction. Both contact resistances are in general function of temperature, powder density and pressure. The accurate estimation of the contact resistances depends on various modeling factors. The functions can be built by laborious combination of modeling and experiments through properly designed calibration and verification procedures [8]. The main experimental and modeling factors are briefly reviewed in the following sections.

Temperature Control and Probing Point Factors

In both Syntex and FCT systems the temperature is controlled by IR pyrometers and/or thermocouples. Typically the probe point is located at the graphite tools rather than in the powder. In the FCT system the IR pyrometer (pyrotop) points downward to the bottom of an axial borehole drilled in the upper punch down to 5mm away from the compact edge. Analogously, in the Syntex system the IR pyrometer (pyrofront) points radially to the outer surface of the die. Alternatively, the pyrofront focuses through a radial borehole running across the die down to any depth, typically 5mm from the sample edge. In most SPS devices, such probing temperatures are used to automatically control the electric power supply via a PID control system. Thus, in both SPS systems the true temperature of the powder is always unknown.

SPS simulations suggest that electrically conducting powders experience a core temperature larger than that measured at the probe point owing to the direct current dissipation across the powder [6,8,12]. Moreover, in FCT and Syntex systems, the related probe points and the powder core are always separated by a contact interface, namely a horizontal and a vertical interface respectively. As contact interfaces, are special non-equilibrium surfaces, large temperature deviations are experimentally observed between the probe points and the powder. An important consequence is that the PID control system in both units may supply an inadequate electric power to the powder and the true temperatures can be either in excess or defect with respect to the user preset temperature.

A current control mode would be safer than the temperature control mode, as the electric power is supplied manually. This has an impact on the choice of the temperature probe points in location and number. Most SPS devices exploit one probe point to control the process. The recorded temperature is often used in simulations to extract the unknown thermal contact resistances of the given SPS system. Some studies provide detailed information on temperature measurement at several locations of the SPS system and on contact resistances. For instance, Matsugi et al. [18] measured temperature using thermocouples located at several points in the graphite tooling as well as in the partially consolidated compact. Manière et al. [10] reveal the thermal effects at contact interfaces by thermal imaging other than by thermocouples located at various points of the device chamber, and of the graphite tools whereas the probe point was located beneath the outer surface of the die.

Pressure and Clearance Factors

Pressure is a key parameter influencing all contact resistances at any dimensional scale. With reference to the SPS of WC powder, for instance, low pressures (5-20MPa) promote high sintering temperatures with consequent abnormal grain growth and highly inhomogeneous microstructure and hardness [21]. Large pressures (60-80MPa), on the other hand, induce the vertical punch/die contact interface to suppress the radial thermal gradient thereby enabling homogeneously dense microstructures. The punch/die contact resistance affects the radial temperature gradient in the WC powder which increases with decreasing pressure [21]. However, the vertical contact resistances in the upper and lower stacks operate quite differently and, as a result, the axial temperature and temperature gradients are qualitatively and quantitatively different thereby breaking the vertical symmetry [6,8,9,17]. This loss of symmetry decreases with increasing temperature and degree of densification. SPS densification models are typically three-way models which couple electrical, thermal and displacement fields consider the inherent shrinkage and the change of powder properties as a function of temperature and density [6,8,9,22] as well as the change of contact resistances as a function of temperature, pressure and density [6,8,9].

Excessively low-pressure during SPS may cause overheating, accidental sparks between graphite elements, powder overheating and poor densification [21]. Conversely, when both pressure and currents are too high, powder particles may undergo significant localized plastic deformation and/or creep [9,16,17,18,22], melting and even vaporization phenomena. Moreover, high contact temperatures induce undesired local stress-strain field upon heating and cooling cycling. Fundamental studies on contact resistances aim at separating horizontal from vertical contact resistances by either replacing the powder with a solid sample or remove the sample. In so doing Giuntini et al. [13] predict that all contact resistances decrease with increasing temperature and pressure and the vertical contact resistance depends on pressure, via the reduction of the clearance between the punch and the die. The latter is originated by both the thermal expansion of graphite punch and elements and the Poisson effect upon compression loading. Conversely, horizontal contact resistances can be considered as negligible in the moderate to high pressure regime [8,12,13], except for any constriction effect accounted by SPS codes. Tiwari et al. [20] characterize the effect of electric, thermal contact resistances by inspecting the change of initial clearances between graphite elements with pressure and temperature and relative contact area. Various thermal conductivities of the sample, radii of the die and heating rates were investigated and compared in terms of radial temperature gradients. The approach of Song et al. [9] is unique in that they study the effect of contact resistances during the SPS of powder, including shrinkage, using an insulating die. Consequently, their contact resistances are expected to be at least much different compared to those with graphite dies.

Model Calibration and Validation

Before using, SPS models must be calibrated and validated against experiments. Typically, the quantities selected for calibration and validation are the electric and thermal contact resistances. The field variables chosen for the calibration are mostly the temperature and voltage. These variables are recorded at some points in the SPS system. Earlier SPS models utilized constant electric and thermal contact resistances. Recent SPS models implement more complex functions of temperature [e.g: 5,7,8,11-13,20] and pressure [e.g: 8,11,20]. More robust SPS models may also include shrinkage [8] and electric power recordings [12]. More simply Zavaliangos et al. [5] assume the same temperature dependence for both the contact resistances and the bulk resistivity of tool graphite. The temperatures are measured by thermocouples at selected points and/or by IR pyrometers at specified probe points. Conversely, more complex temperature functions of both electric and thermal contact resistances, can be determined by invoking an iterative procedure, starting with published constant electrical and thermal resistances, tightly combining experiments with modeling, until the overall functions are defined within the selected process window of parameters. Matsugi et al. [23] neglect the effects of contact resistances and attempt a quasi true powder-core temperature measurement using a two-step SPS: a) sintering the powder to attain an intermediate density, b) final sintering to full density. Vanmeensel et al. [12] use three specially designed SPS tools the temperature was measured by a K-thermocouple running across a borehole drilled radially across the die and the compact assembly. They derive the horizontal and vertical contact resistances as a function of temperature, taking into account the presence of GFs at selected interfaces. Temperatures are monitored by the main pyrotop and a secondary pyrofront focusing respectively at the bottom of the axial bore hole drilled along the upper punch down to 5 mm away from the sample edge and at the outer surface of the die. The related SPS model predicts quite inhomogeneous distributions of electric and thermal fields, hence strongly suggesting the crucial importance on the most suitable location of probe points for calibration and validation purposes. The authors conclude that the temperature gradient across the solid compact markedly depend on the contact resistances and the electric properties of the sample. The major electric and thermal contact resistances in the system act at the punch/sample and die-sample interfaces. The repeatibility in the estimated contact resistances upon SPS with WC powder is assessed by Grasso et al. [21] using one single IR pyrofront focused at two alternate focusing probe in dual SPS experiments. Tiwari et al. [20] estimate the electric and thermal contact resistances as a function of the recorded temperature in concomitant with the geometrical change of the gap width between the graphite elements which, in turn, depend on loading and thermal expansion of graphite tools.

Micro-macro Temperature Gradient Factor

Electric contact theory suggests that, neglecting the constriction effect, which is accounted naturally by solving the Laplace’s equation, the average temperature at a contact interface results from the temperature jump originated by the current dissipated across conductors’ pair. This theory applies to both device and particle contact interfaces. Consequently, at the powder level, the contact temperature differences between contact points drive the heat conduction flow across the powder and its sintered aggregates. If the pressure is relatively low, the particles may easily rearrange and heat up rapidly. If the pressure is too low, accidental sparks may occur being facilitated by the interparticle sliding [24]. Identically, at the device scale, macrocontacts act individually as formidable heat sources, which strength and rate of heating, depends on their relative temperature. Especially at the early stage of the SPS process, horizontal macrocontact/macroconstrictions are hotter than the powder and may attain different temperatures, depending on the relative electrothermal conditions set in between them and the powder. Macrocontacts are electrothermally connected to the powder via the graphite tools and operate in the assembly as outer heat sources with respect to the inner powder. As macrocontacts are initially hotter than the powder they behave as powerful heat sources which heat flux is determined by the temperature gradients developed between them across the device. Thus, the horizontal and vertical contact resistances are responsible of the axial and radial contact heat conduction. Such a heating of the powder under crossed temperature gradients induced initially by the macrocontacts and more intensively by the macroconstrictions, explains the advantages and disadvantages of SPS. From the one hand, by controlling the macrocontact resistances extremely fast heating and cooling rate can be obtained, as proved by several publications. On the other hand, such temperature gradients are just the cause of both density and microstructure gradients in the sample, respectively throughout the powder. The most active macroconstrictions, on the initial heating of a metallic powder, are usually those between the horizontal rams or spacers nearest to the electrodes. These contacts set the primary temperature gradient that drives the axial heat flow to the powder by means of the upper and lower assemblies. The rate of heat flow to the powder is proportional to the temperature gradients and the electrical resistances of the powder [12]. Electrothermal fields in a SPS system are determined from the instantaneous electrical and thermal conditions at all macrocontacts and macroconstrictions and their balance with and the eletrothermal properties of the shrinking powder. The predictions [5] confirmed that conductive powder is initially heated indirectly by the punches and in the later stage is manly heated indirectly by the die. However, the predicted temperature ratio of the sample core to the die surface is three times larger than the measured one. The main cause of this anomaly, among other factors, can be attributed to the neglected vertical punch to the die thermal contact resistance.

SPS Models Based on Contact Multiphysics

The purpose of this section is to briefly review some of the published SPS models that embody the contribution of contact resistances to some extent. For reasons, the list of publications cannot be complete and is simply representative of the efforts made throughout the world on this subject. Most contact studies [4-8,10,12,13,17,19,20,25,26] have been aimed at correlating the predicted temperature gradients with the observed microstructure inhomogeneities. The ever-increasing number of such publications bears witness to the crucial importance of contact interfaces in controlling the compact microstructure through control of the SPS phenomena. Various authors have proposed axisymmetric or full 3D SPS geometric models using a two-way electro thermal [5,18] or a three-way electro-thermal and displacement or residual stress field [8,16,25,26]. Some of these models have been addressed to the minimization of thermal gradients in solid samples [5,13,16,19,20,26], the comparison of electro-thermal phenomena in both conductive and insulating powder [10,12,16,17,25,26], the design of novel tools in order to uniformize microstructure especially in large net-shaped compacts [11-13,25], to analyze the fundamental aspects of contact resistances e.g: [5,8,20,26], to inspect the influence of graphite foils (GFs) on SPS phenomena, especially temperature gradients e.g: [5,8,12], to analyze the effects of residual stresses e.g: [16,25,26] and to investigate the influence of SPS process parameters e.g: [6,25]. In nearly all of these models, the electric and thermal contact resistances have been treated as lumping parameters and, thus, empirical quantities of the specific SPS system which includes as the device and the powder. Various predictions supported by experiments, have shown that when the macrocontact effects are neglected, the electric conductivity of the sample has a marked impact on the temperature distribution near the die/sample interface [16]. The current density is higher in the die, near its edges, when heating solid alumina, whereas it is higher in the sample, near the die wall, when conductive samples are heated. Consequently, thermal gradients are more uniform in alumina samples than in the conductive ones. Moreover, the radial displacement increases fairly uniformly with the radius. The highest displacement is attained near the die surface, due to combined thermal and load-dependent Poisson expansions effects. Some model results [5-7,11-13,16,25] agree in that the vertical contact resistance is dominant over the horizontal ones. However, very few models have considered the powder shrinkage and/or the effect of the sliding vertical contact resistance [6,8,9,17]. This lack factor has an inevitable impact on the reliability of a model and its comparability with other models. In other cases, comparability has been compromised by the lack of sufficient information on the contact conditions (e.g., initial clearance, cleanness), the presence of either contact films or GFs and inherent geometrical and physical properties.

Exceptional care should be taken when modeling the sliding vertical contact, due to its relevance in shrinkage problems. The sliding feature is efficiently described using the moving mesh technique [8] by specifying the recorded shrinkage-time curve at the punch edge in contact with the powder. This approach faithfully describes the electrical and thermal fields, provided a prior robust calibration and validation procedure have been conducted. The advantage of moving mesh approach is that sufficiently accurate distributions of the electric and temperature fields can be predicted without any prior knowledge of the actual sintering mechanisms in the powder. When shrinkage and sliding effects are ignored, the temperature and current flow fields are axially symmetric. Finally, appropriate temperature and density functions of powder properties, other than temperature functions for both the powder and the bulk graphite have to be formulated, see e.g: [8,12].

Wei et al. [11] studied the effect of the horizontal and vertical contact resistances by comparing two tool assemblies, one machined as monolithic, i.e., without any contact interface, while the other included two main contact interfaces around the sample boundaries. However, no constrictions or horizontal contacts were designed between the electrodes, rams and spacers. The computed contact resistances were then used to examine the effect of the horizontal and vertical contact resistances on the electrical and thermal fields. However, the model ignored the major role played by the contact resistance effects the rams and spacers which are significant in real SPS devices. Wang et al. [25] reported that the size of the die shows a non-linear effect as it has a marked influence on the uniformity of the temperature in the sample. This result should be interpreted in terms of variable coupling, through electrical and thermal fields, between the punch/die resistance and the vertical contact resistance.

The practical importance of contact resistances is better understood when the SPS is applied to semiconductor powders. It has been shown experimentally and confirmed through simulations that p-type (resp. n-type) semiconductors can suffer the Peltier effect during SPS [15,27] and that, accordingly, one contact edge of the sample is cooled while the other contact edge is heated. The Peltier effect leads to temperature redistribution and to a density gradient across the thickness of the sample. More importantly, the pyrotop in the FCT device detects any temperature that is in excess (resp. in defect) of that at the sample core [15]. As a result, the true sintering temperature is lower (resp. greater) than that preset by the user. Consequently, the compact is under heated (resp. overheated) which explains the poor sinterability of semiconductors by SPS [15,27].

Grafite Foil effects

The insertion of graphite foils (GFs) between graphite elements and between graphite elements and the powder complicate even further the mastering of SPS phenomena. These foils are special thin sheets of artificial graphite in which the electrical and thermal properties in the in-plane and throughthickness directions are significantly different. Moreover, these properties change considerably with temperature [12] causing hot spots and large temperature gradients between macrocontacts in the SPS system. A beneficial effect of such temperature gradients, although not properly correlated with them in the current practice of SPS, is the inherent high heating and cooling rate across the sample. Because of the high heating/ cooling rate features, the number of SPS studies using GFs has been increasing [5,6,8,10-12]. It is more generaly claimed that GFs can prevent the sticking of the powder to the graphite tools and can reduce wear especially at the sliding vertical contact. Due to such a routinely use, the presence of GFs is not adequately documented in the published papers. However, it is has recently been recognized [6,8,10,12] that GFs have additional effects: a) high ability of current dissipation along the through-thickness direction, b) fast dissipation of heat along the in-plane direction. Thus, the inclusion of GFs at the macrocontact interfaces provides an effective means to augment the indirect heating of the sample (regardless its electrical conductivity) through the inherent temperature gradients. A counter effect of heating under such macrocontact- and/or macroconstriction-based temperature gradients is the commonly observed radial and/ or axial microstructure inhomogeneities in powder compacts. Zavaliangos et al. [5] investigated, both experimentally and computationally, the effect of GFs at the punch/sample interfaces in the case of a solid graphite sample. They report that Joule effect in GFs was initially negligible due to the small thickness of the sheets. Initially, the predicted temperatures were uniform across the sample. Conversely, significant temperature gradients and heating rates were predicted in the later stage of SPS. Munoz et al. [26] state that GFs should be avoided at the vertical sliding contact GFs when SPS is performed in non-conductive samples as they increase the radial temperature gradient across the sample particularly in the case of very small and very large sample diameters. The existing differences between the measured and true powder temperatures due to the presence of punch/ sample and punch/die contacts resistances can be enhanced by the presence of GFs although with unfortunate consequences of process control.

SPS Contact Multiphysics

Any further developments of the ECAS technology would requires modeling of the shrinkage phenomena in the powder to be coupled with the combined effect of electrical, thermal and stress-strain fields, so that the micro-macro phenomena are traced simultaneously [9,14,17,22,25]. Di Napoli et al. [22] reported successful agreement between a full micro-macro multiphysics model and experiments for the case of the capacitor discharge sintering (CDS) of a copper-diamond mixture and graphite tooling as in SPS systems. The electric, thermal and displacement fields were solved sequentially and selfconsistently, within a moving mesh framework, along with plastic deformation-based densification phenomena, during a single current pulse discharge. It should be noted that the horizontal contact resistances in CDS are quite negligible because of the imposed pressures are much larger than in SPS. Nevertheless, the significance of the sliding vertical contact resistance in both processes is similar. Mondalek et al. [17] predicted shrinkage kinetics in TiAl compacts by coupling the viscoplastic constitutive law, in the powder, with electrothermal phenomena. However, the sliding contact contribution associated with the vertical contact resistance as well as with its temperature and pressure dependence were ignored. Schwertz et al. [14] solve a three-way electric, thermal and stress-strain fields coupling together with the Cam-Clay shrinkage model in the powder without considering the effect of contact resistances.

Conclusion

Both experimental and numerical studies on contact resistances are steadily increasing in order to understand SPS phenomena and to better control the microstructure inhomogeneities in the compacts. Contact Multiphysics has been proposed as more appropriate approach to control SPS phenomena at both a microscopic and a macroscopic scale as it captures the dominant role played by all varieties of contact interfaces in the SPS systems. The development of a comprehensive contact multiphysics methodology requires the appropriate integration of experimental and computational techniques. In-situ temperature measurement is highly desirable as the indirect temperature measurement currently represents the most limiting factor in both process control and reliable SPS modelling. SPS models are expected to contain more precise information about the factors and conditions that influence SPS contacts at both a microscopic and a macroscopic scale. The initial clearances as well as location, geometry and properties of the graphite foils should be specified in much more detail. The electrothermal effects of the vertical-sliding contact interface is an essential factor of SPS and should in particular be included in all SPS models to permit a fair comparison between various models and experiments. The development of micro-macro SPS models should be highly encouraged to augment a sounder SPS science at withall scales of the process, being a fundamental prerequisite for the aimed SPS fabrication of materials by design. A greater reliability of SPS models will be ensured when the developed multiphysics of contact interfaces in SPS models will concurrently match the recorded temperature, voltage drop, shrinkage and overall electric resistance.