Journal Material Science | Open Access Publishers

Review Article

A Correlation between Localized States and Meyer-Neldel Relation in Crystallization Process of Amorphous Sete Films

Bhargava A*

Department of Physics, Dungar College, India

Submission: August 11, 2017; Published: September 12, 2017

*Corresponding author: Bhargava A, Nanophysics Laboratory, Department of Physics, Dungar College, Bikaner-334001, India, Email: anamib6@gmail.com

How to cite this article: Bhargava A. A Correlation between Localized States and Meyer-Neldel Relation in Crystallization Process of Amorphous Sete Films. JOJ Material Sci. 2017; 2(5): 555597. DOI:10.19080/JOJMS.2017.02.555597

Abstract

Electrical conductance is measured in amorphous SeTe films to investigate the crystallization mechanism in the system. The crystallization is found to occur at the sample-substrate interface. The Arrhenian temperature dependence of crystallization velocity estimates the activation energy. The Meyer-Neldel relation (MNR) has been observed in amorphous SeTe films through a correlation between pre-exponential of growth velocity and activation energy. The presence of localized states in amorphous chalcogenides and its relation to viscosity for controlling crystallization mechanism in films is discussed.

PACS: 71.23.-k; 72.15.Cz; 73.61.Jc; 77.84.Bw

Introduction

Crystallization in amorphous Se-Te binary and ternary alloys has been studied using various techniques such as Differential Scanning Calorimetry (DSC) [1], Differential Thermal Analysis (DTA) [2-3], Electron Microscopy [4-5] etc. The electrical conductivity has been previously used to determine the crystallization process in amorphous bulk alloys [6-7]. Since in chalcogenides, the conductivity of the amorphous state is lower than that of crystallized state, the electrical measurements are expected to be very sensitive to the phase changes in thin films in comparison with other conventional methods such as DSC or DTA [8]. This paper describes an attempt to deduce from the crystallization kinetics, the growth rate and activation energy when the crystallization is induced at the sample-substrate interface.

Experimental Details

The Se: Te films were prepared by vacuum evaporation technique onto degassed glass substrates held at room temperature. The Te content of the prepared samples was 0, 10, 20 and 30 at. % of Se. The thickness was kept constant and was measured to be 750nm. The X-ray diffraction pattern showed that the samples were amorphous in nature. Before evaporation of the thin films, Indium electrodes of about 1mm thickness were deposited on the glass substrates. The contacts were found to be ohmic in the present voltage range of measurements. The electrical measurements were made by applying a voltage of 5V to the samples. The sample current was measured by measuring the potential drops across a resistance connected in series with the sample using a digital micro voltmeter (Systronics). The samples were annealed at various temperatures (333K - 348K), which were chosen to observe crystallization in appropriate crystallization velocities. A vacuum of 5*10-3 Torre was maintained during the entire procedure.

Results and Discussion

When nuclei covers a surface of radius r and when r is large compared to the thickness of the layer, e , then the crystallization occurs similar to an epitaxial growth, the crystalline phase reaching the opposite surface of the layer at a time t=e/v_c (v_c is the growth rate) [9]. This is referred to as Surface Induced Crystallization (SIC). Such crystallization is actually polycrystalline It has been shown that at any given time t, the conductance of the layer can be written as

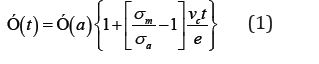
where σ_m is the conductivity of the partially crystallized layer during the annealing process and σ_a is the conductivity of theamorphous layer [10]. The crystallization velocity was obtained through the measurements of τ (time at which the linearity of Σ(t)/Σ(a) curve breaks off). The conductance variation during the isothermal annealing of amorphous films of Se:Te (Te = 0-30 at.% of Se) is shown in Figure 1. The crystallization time τ was obtained at each annealing temperature and corresponding growth rates v_cwere calculated.

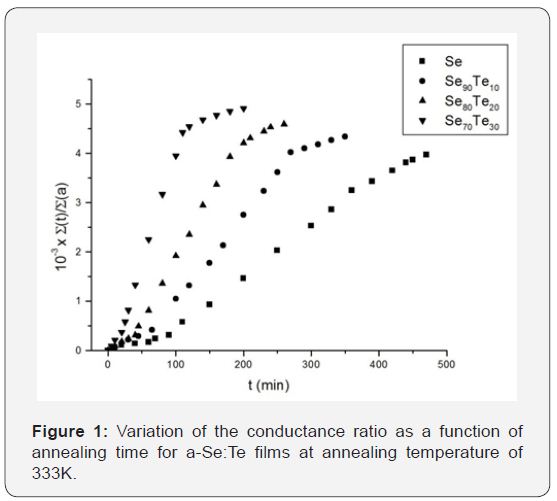
The crystallization process was seen to occur in three stages. During the first stage (0o), conductance increases quadratic ally with time as the fit of the data has predicted. It has been shown that the crystallization in a-Se: Te films occur in a twodimensional way at the interface [5]. Above two-dimensional crystallization leads to a quadratic variation of conductance with time [8]. During the second stage (t_oc). The crystallization velocity obtained using the above relation for Se₈₀Te₂₀ film as a function of temperature is shown in Figure 2. The behavior for all compositions is the same. Similar behavior was also observed in bulk glasses [6]. Finally, the conductance saturates for t >τ. The saturation of the conductance relation after time τ results from the crystallization of the rest of the amorphous domains in the thin films. This occurs as all the nucleation sites were exhausted and the growth of the crystallites stops, i.e., site saturation [10].

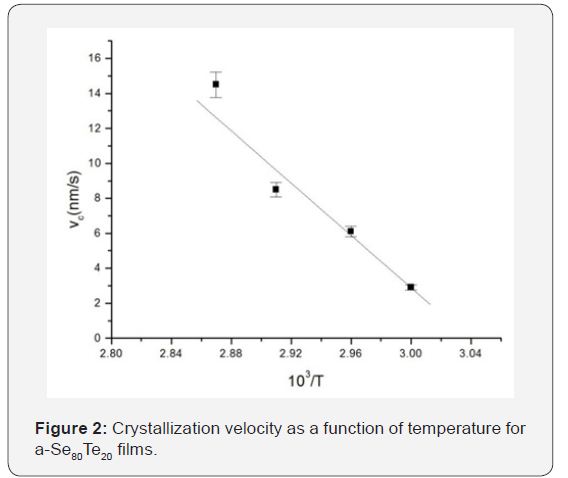
The crystallization velocity obtained in the experiment was found to decrease continuously with increasing Te concentration at each of the annealing temperatures. As is evident from Figure 2, the crystallization velocities show a thermally activation behaviour with an Arrhenian dependence for each of the composition given by [11]

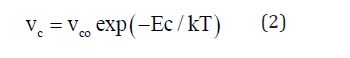
Figure 3 shows the dependence of the activation energy E_c of crystallization on the Te content. The pre-exponential of crystallization velocity also show same type of behavior. In the range x=0 to 20 at.% in Se: Te films, both E_c and v_co decrease monotonically. The Te induced retardation was also observed in the melt quenched bulk glasses studied by us [6] and others [12]. With a further increase in Te, these quantities go through a minimum at 20 at.% Te. A similar compositional dependence of the activation energy of crystallization has been reported in melt quenched Se: Te bulk glasses by Ganaie et.al. [13].

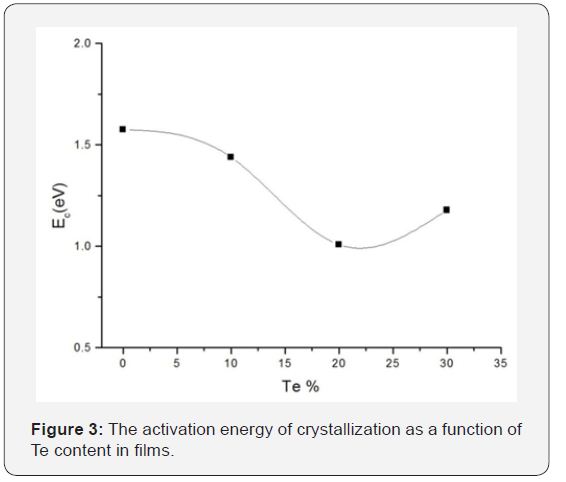
The minimum in E_c can be understood as follows. The cis- (ring segment) and trans- (helical chain segment) configurationsin amorphous Se differ only in the placement of the 5th neighbor atom for molecular bondings [14]. The placement of the likely atom depends on the competition between the intra-chain and inter-chain forces. It is expected that the number of cisconfiguration starts to decrease near this configuration with increasing Te content, because the intra-chain force of Te is weaker than that of Se. The intra-chain force decreases and the inter-chain force increases with the addition of Te atoms to a-Se. The minimum activation energy at the particular Te concentration is therefore, likely to be attributed to such an intermediate range structural modification. The increase of glass transition temperature with Te concentration also indicates increasing chain lengths of Se-Te [15] and hence to a more rigid network.

Figure 4 shows the plot of the pre-exponential factor vco versus the activation energy E_c of the crystallization velocity in thin films. There is a very good correlation between the v_co and E_c, often referred to as the Meyer-Neldel relation [16] and is described as

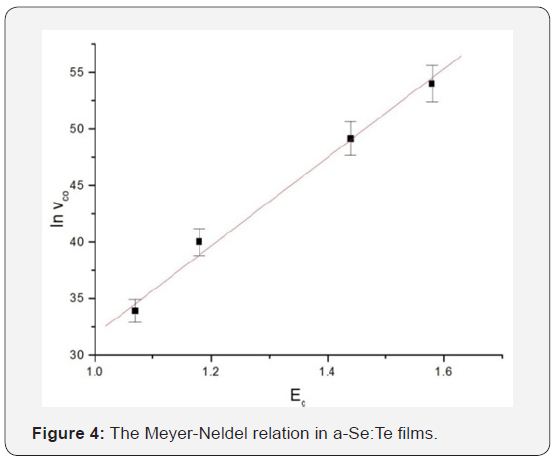
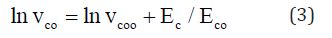
Where v_co is a constant with a value of about 1.8*10-3nm/s and E_co~0.0483eV as deduced from Fig.4. Here, the obtained value of Meyer-Neldel energy is 48.3meV, which is well within the range 25-100meV generally reported in semiconductors [17]. This energy corresponds to Meyer–Neldel temperature equal to 560K , that is within the reported range of temperatures 260-950K [ 18].

Assuming that the crystallization velocity in amorphous materials is inversely propotional to the viscosity of the melt η [12], which has a Vogel-Tammann-Fulcher type of behaviour [19], i.e., η=η_o exp (E_o / k (T-T_o)), where η_o, E_o and T_o are constants, then the crystallization velocity becomes

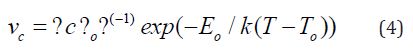
This equation is almost indistinguishable from Eqn. (2) in a narrow range of temperature except for the vicinity of T_o. Moreover, if we try to fit the Arrhenian dependence of v_c in a temperature range T₁ to T₂ , we obtain [5]

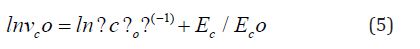
Where

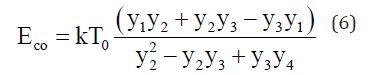
y₁=a-b, y₂= ln(a/b), y₃=ln{(a - 1)/(b - 1)}, y₄= (1/b)-(1/a), a= T₂/T_o; b=T₁/T_o.

The estimated Eco value of 0.0325eV is obtained using T₁=330K, T₂=360K and T_o=303K. This is an indication that the crystallization velocity in a-Se:Te films can be considered to be controlled by the viscosity of the melt. The variation in Vicker’s hardness in chalcogenides around crystallization temperatures also allows us to correlate our results with viscosity [20]. The increase in glass transition temperature with Te concentration is a good indicator of the increase in viscosity with Te [21].

Although the Meyer-Neldel relation has been observed in various physical systems, there is still no satisfactory uniform explanation for its occurrence. Several mechanisms to explain the origin of MNR in semiconductors have been proposed. Jakson [22] argued that whenever a multiple trapping transport process is observed as a function of temperature, MNR should be followed. Abtew et al. [23] have performed a comparative study of MNR in crystalline Si and non hydrogenated amorphous silicon and claimed that MNR is present in amorphous silicon only. They suggested that the existence of localized state and the energyelectron lattice coupling for these states is an essential feature of MNR in silicon amorphous phase. Thus, MNR presence is closely connected to the presence of band tail of localized states which are generally assigned to the disorder in film network.

In disordered semiconductors, three conduction mechanisms may occur:

Hopping from one localized sates to another localized state.
Carrier hopping from localized state to an available extended state.
Carrier scattered from one extended state to am empty extended state.

The first two conduction mechanisms require phonon assistance. Transition (i) and (ii) plays a role at low and moderate temperature. However the transition (iii) may be significant only in higher temperature. The conductivity in the films is governed by the multi-trapping process in band tail localized states and explains the MNR observation in films.

The present system gives a wide band gap semiconductor with exponential localized tail states proposed by Roberts [24].Since the conduction mechanism in films involves localized states, the electronic transport is achieved through electrons trapping and detrapping by multi-phonon process with the contribution of many phonons. This conduction model was first suggested by Yelon and Movaghar to explain MNR in thermally activated conduction [25]. In localized states conduction, the activation energy of the transition from localized state with energy Ei to an empty localized state with energy Ej is given by [26].

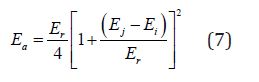
Where E_r is the reorganization energy of the semiconductor random network for carrier hopping and is expressed as

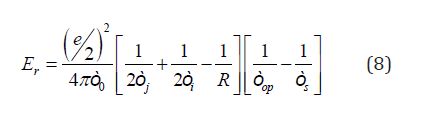
Where ϵ_i and ϵ_j are the localization radii for the two localized states, R is the distance between the two localization centers [27], e is the elementary electric charge, ϵ₀ is the vacuum dielectric constant, ϵ_op and ϵ_s are optical and static dielectric constants respectively. With increasing the disorder, the distance R increases and the film density decreases, consequently the film refractive index and optical dielectric constant are reduced [28,29] This leads to the increase of the two square brackets in Eq. (8) and then to the increase in the reorganization energy E_r and consequently the reduction of the activation energy E_a.

Conclusion

The conductance measurements carried out on SeTe glassy films between the glass transition and crystallization temperatures provides information about the crystallization mechanism in thin films. During the early times, the crystallization is due to nucleation and conductance varies quadratically with time. When the nucleation is completed, the conductance varies linearly and the process occurs as a result of growth of crystallites towards the surface. The addition of Te reduces the growth and activation energy show a minimum at x=0.6. Meyer Neldel relation is found to be obeyed in the present case through pre-exponential of velocity and activation energy. This can be assigned to an increase in localized states resulting in increase in viscosity of the specimen around Te 60 at%.