Lagrangian-Euler Equations, Navier-Stocks Equations Combined with Bernoulli Equation and the Lagrangian Coherent Structure Methods to Assess the Best Mitral Valve Modeling of the Heart and Blood Fluid Movements in the Mitral Valve
Mersedeh Karvandi and Saeed Ranjbar*
Taleghani Hospital, Shahid Beheshti University of Medical Sciences, Iran
Submission: March 10, 2018; Published: May 11, 2018
*Corresponding author: Saeed Ranjbar, Taleghani Hospital, Shahid Beheshti University of Medical Sciences, Tehran, Iran, Email: sranjbar@imp.ir/ saeed.ranjbar@mumc.nl
How to cite this article: Mersedeh K, Saeed R. Lagrangian-Euler Equations, Navier-Stocks Equations Combined with Bernoulli Equation and the Lagrangian Coherent Structure Methods to Assess the Best Mitral Valve Modeling of the Heart and Blood Fluid Movements in the Mitral Valve. J Cardiol & Cardiovasc Ther. 2018; 10(5): 555790. DOI: 10.19080/JOCCT.2018.10.555790
Abstract
This article reviews and combines different mathematical methods and techniques in order to model the mitral valve of heart and blood fluid movements in the vicinity of the valve. Currently, an echocardiogram is the best thing to study the morphology of the heart mitral valve based on images obtained from ultrasound methods. Utilizing mathematical equations and methods, specific echocardiographic data may provide more detailed, valuable and practical information for physicians.
The problem is a tissue-fluid interaction. A 3D mitral valve tissue modeling states a boundary condition to study the blood fluid dynamic around the mitral valve. The body force interacted between the fluid and mitral valve leaflet tissues, combined with the general Lagrangian-Euler equations, gives a fibered model of the mitral valve. This fibered model presents a boundary condition for the solution of the Navier-Stocks equation combined with Bernulli's equation of the blood fluid around the valve. Resulting from the velocity field data due to the convolution of the Euleran velocity from Navier-Stocks equation combined with the Bernoulli's equation with 3D Delta function and the other velocity vector field of the blood flow movements due to the convolution of the solution of Lagrange-Euler equations with 3D Delta function, we can apply Lagrangian coherent structure (a vector flow mapping method) in order to study topology of blood transport in the mitral valve per cardiac cycle.
Keywords: Navier-stocks equation; Lagrangian-Euler equations; Echocardiography; Mitral valve of heart; Lagrangian coherent structure; Vector flow mapping
Anatomy of the Mitral Valve of the Heart

The human heart has 4 valves. The mitral valve connects the left atrium (LA) and the left ventricle (LV). The mitral valve opens during diastole to allow the blood flow from the LA to the LV. During ventricular systole, the mitral valve closes and prevents backflow to the LA. The normal function of the mitral valve depends on its 6 components, which are (1) the left atrial wall, (2) the annulus, (3) the leaflets, (4) the chordae tendineae, (5) the papillary muscles, and (6) the left ventricular wall (Figure 1) [1-5].
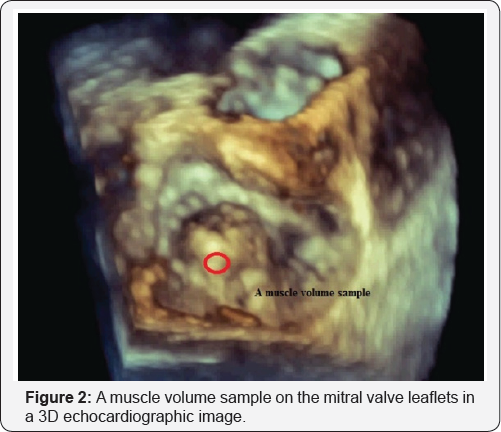
A 3D echocardiogram image data at the level of the mitral valve shows completely the anterior and posterior mitral valve leaflet tissues. A muscle volume sample on the mitral valve leaflets is realized as a geometrical point in the 3D space (Figure 2).
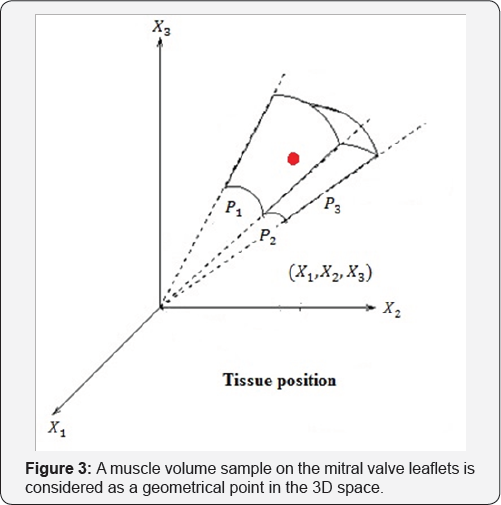
We attach a system of coordinate to these geometrical points we can able to present the motion and deformation components. Joined Cartesian tissue position (X1,X2,X3) on the mitral valve leaflet with curvilinear coordinate (P1,P2,P3), we have a new coordinate for considered tissue q = (qi, j) = (Xi + Pj) i,j =1,2,3. (Figure 3 a simple shape for this new coordinate).
Let sq ,vq and ei,j,q such that i, j = 1,2,3 are displacement, velocity and pure strain components attached to the point "q". And let lq be a fibered curve on the mitral valve leaflet which passes from point q at time t. Point "q" can be explained by two variables 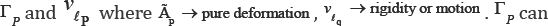
 We can reformulate the force parameter over the time at point "q" by this partial differential equation
We can reformulate the force parameter over the time at point "q" by this partial differential equation
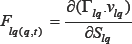
Fibered curve generated by point "q" within a cardiac cycle based on velocity, strain, force vectors and generalized Lagrangian equations:
The next step is to design mathematical equations to find the rout which passes from "q" based on Lagrangian-Euler equations. Lagranjian-Euler equations for point "q" is described by the following reformulation based on echo datasets:
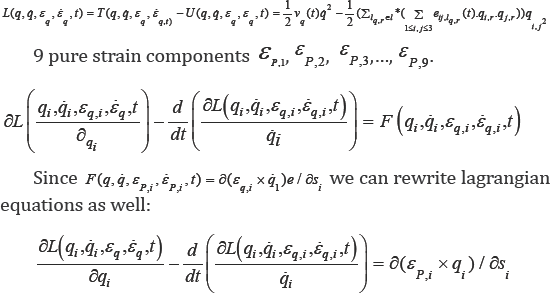
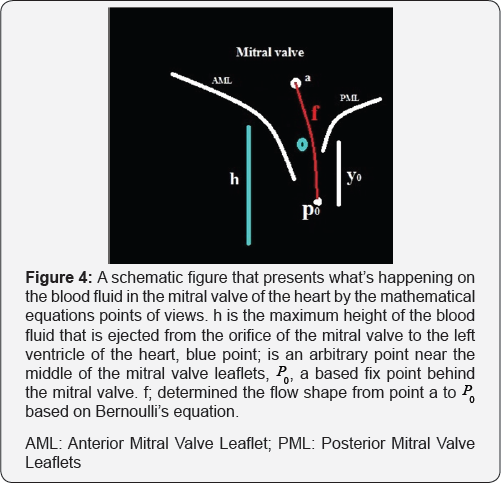
The solution of these equations generate a fibered rout where passes from point "q" within the cardiac cycle. We call it Rq . Combining Navier-Stocks equation and Bernoulli's equation, one can make a solution of a new system of partial differential equations of the blood fluid velocity around the mitral valve (Figure 4).
At first, The problem is to determine the shape f(y) of a wire equation notch (here the notch is considered the orifice of the mitral valve and a wire equation is realized by the streamline flow behind the mitral valve and a modeling of mitral valve leaflets), an opening in mitral valve leaflets, in which the volume flow rate of fluid, Q, through the orifice is expressed as function of height h of the orifice.
Assuming Bernoulli's equation can be applied between the point "a" and "y" in Figure 4 [6,7], we obtain
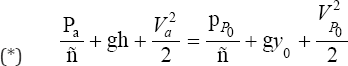
Where 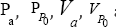 are the pressures and velocities at point "a" and "P0”; g is the graviational acceleration and ρ is the fluid density.
are the pressures and velocities at point "a" and "P0”; g is the graviational acceleration and ρ is the fluid density.
The pressures at "a" and "y" are both taken to be nearly atmospheric so that Pa = Pp0 and the velocity at "a" is assumed to be negligible (Va = 0) since the fluid behind the orifice is slow moving. Thus, (*) becomes

Let, P and fb are velocity, pressure and force of the blood fluid respectively. f is the derivation of the shape of blood fluid movements exit from the orifice of the mitral valve and near the mitral valve (Figure 4).
We Modify Navier-Stocks equations by the above assumption:
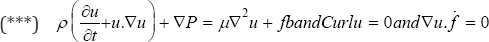
Such that is 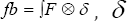 is the 3D Delta function. Solving (***) gives "u" as the velocity vector field of the blood fluid around the mitral valve.
is the 3D Delta function. Solving (***) gives "u" as the velocity vector field of the blood fluid around the mitral valve. 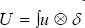 is realized as the Lagrangian velocity of the blood fluid around the mitral valve and
is realized as the Lagrangian velocity of the blood fluid around the mitral valve and 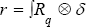 is considered as the Lagrange-Euler velocity of the blood fluid [8-11].
is considered as the Lagrange-Euler velocity of the blood fluid [8-11].
Lagrangian coherent structures (LCS) can be applied to study blood transport in the mitral valve of heart. Resulting velocity field data were used to perform trajectories-based computation of. LCS were shown to reveal the boundaries of blood injected and ejected from the mitral valve over multiple beats.
We define two trajectories x(t,tp,p) and y (t,tp,p) for the mitral valve by the following way:
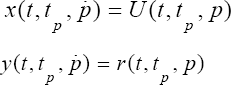
This enabled qualitative and quantitative assessments of blood transport patterns and residence times in the mitral valve of the heart [12-17].
References
- Reul H, Talukder N, Muller EW (1981) Fluid mechanics of the natural mitral valve. J Biomech 14(5): 361-372.
- Saber NR, Gosman AD, Wood NB, Kilner PJ, Charrier CL, et al. (2001) Computational flow modeling of the left ventricle based on in vivo MRI data: initial experience. Ann Biomed Eng 29(4): 275-283.
- Baccani B, Domenichini F, Pedrizzetti G (2003) Model and influence of mitral valve opening during the left ventricular filling. J Biomech 36(3): 355-361.
- Daebritz SH, Sachweh JS, Hermanns B, Fausten B, Franke A, et al. (2003) Introduction of a flexible polymeric heart valve prosthesis with special design for mitral position. Circulation 108(Suppl 1): 11134- 11139.
- Pierrakos O, Vlachos PP (2006) The effect of vortex formation on left ventricular filling and mitral valve efficiency. J Biomech Eng 128(4): 527-539.
- Brenke WC (1922) An application of abel's integral equation. American Mathematical Monthly 29(2): 58-60.
- Bernoulli's equation is strictly valid for steady, frictionless flow in a stream tube. It is used, however, in engineering for flows with friction by modification of solutions with a suitable friction factor
- Ranjbar S, Karvandi M (2014) Mathematical modeling applied to the left ventricle of heart. Cornell University Library
- Ranjbar S, Karvandi M, Hassantash SA, Foroughi M (2014) How to construct a 3D mathematical/computer model of the left ventricle. Arch Cardiovasc Imaging 2(2): e20628.?
- Ranjbar S, Karvandi M, Ajzachi M (2013) System and method modeling left ventricle of heart. US Patent 2013; patent number 8,414,490.
- Ranjbar S, Karvandi M, Ajzachi M (2014) Solution Navier-stocks equations of the blood as a non- Newtonian fluid in the left ventricle. US Patent number: 8805663.
- Haller G, Yuan G (2000) Lagrangian coherent structures and mixing in two-dimensional turbulence. Physica D: Nonlinear Phenomena 147(3- 4): 352-370.
- Haller G (2001) Distinguished material surfaces and coherent structures in 3-dimensional fluid flows. Physica D: Nonlinear Phenomena 149(4): 248-277.
- Haller G (2001) Lagrangian structures and the rate of strain in a partition of two-dimensional turbulence. Phys Fluids 13(11): 33653385.
- Haller G (2002) Lagrangian coherent structures from approximate velocity data. Phys Fluids 14(6): 1851-1861.
- Shadden SC, Lekien F, Marsden JE (2005) Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional a periodic flows. Physica D: Nonlinear Phenomena 212(3-4): 271-304.
- Sotiropoulos F, Webster DR, Lackey TC (2002) Experiments on Lagrangian transport in steady vortex-breakdown bubbles in a confined swirling flow. J Fluid Mech 466: 215-24






























