Review Article

Missing Observations - Method of Analysis

Mariyamma Philip* and DK Subbakrishna

Department of Biostatistics, National Institute of Mental Health and Neurosciences, India

Submission: May 03, 2017; Published: December 19, 2017

*Corresponding author: Mariyamma Philip, Associate Professor, Department of Biostatistics, Dr. MV Govindaswamy Centre, NIMHANS, Bangalore, India-560 029, Tel: +91 94484 66671; Email: dr.mariammaphilip@gmail.com

How to cite this article: Mariyamma P, DK Subbakrishna. Missing Observations - Method of Analysis. J Complement Med Alt Healthcare. 2017; 4(5): 555646. DOI: 10.19080/JCMAH.2017.04.555646

Abstract

Background: Missing data are a problem, especially in large epidemiological studies or in longitudinal studies on chronic illnesses or in public health research relying on routinely collected data. Imputation, the practice of filling in missing data with plausible values, is an attractive approach and several techniques of imputations exist.

Aims: The present paper describes missing data mechanisms and examines different imputation techniques to fill in the missing values of the outcome variable in a prospective study.

Methods: The data for the present investigation came from a prospective study designed to find out the predictors of early response to treatment in drug-naive Schizophrenia patients. The total scores obtained on Positive and Negative Symptom rating Scale (PANSS) scale was the outcome of the study. The present paper attempts to compare four different imputation techniques-single value imputation, EM imputation, regression imputation and multiple imputation, in filling up the missing values of the outcome variable.

Result: Outcome, the PANSS scores were missing for about one-third of the subjects (32%) at the sixth week. None of the imputation techniques resulted in values that were significantly different from those of the complete cases. The outcome values were deleted for a proportion of complete cases selected at random and the missing value analyses were then carried out. The results showed that imputed values significantly differed from the complete cases only when the rate of missing observation was very high.

Conclusions: The results of this investigation did not show significant differences between the values of complete cases and imputed values obtained by various techniques, and it can also be seen that the efficiency of the techniques depends on the rate of 'missingness'. These results should encourage researchers to employ the method of imputation, which is generally viewed with lot of suspicion, to fill in the missing values. It has been generally observed that many researchers are apprehensive as well as unaware about imputation techniques. This paper can be viewed as an introduction to the basics of imputation and the authors aim to encourage the researchers to adopt the imputation techniques while facing the problem of missing data

Keywords: Missing data; Missing data mechanism; Imputation

Key Messages

a) Missing observations are a problem in any field of research.

b) Missing value analysis helps address several concerns caused by incomplete data.

c) EM imputation using SPSS could be an appealing solution to the problems of missing observations.

Introduction

In an ideal data collection process, data would exist for all variables across all experimental units. Unfortunately, for a number of reasons it is possible that some values could not be collected, could be lost, or could not be used. For instance, an individual may respond only to certain questions in a survey, or may not turn up for a schedule in a longitudinal survey. So, missing data are simply observations that one intended to measure but did not, because of some unavoidable reasons. Even in the presence of missing data, the research goal remains same, making inferences that apply to the population targeted by the complete sample - i.e. the goal remains what it was if the researcher had seen the complete data.

It is a well known fact that the analysis of randomized complete block design depends on having all the treatments in each block. Sometimes observations in one of the blocks could be missing in a randomized complete block design. This may happen because of carelessness or error or for reasons beyond the control of the investigators. This introduces a new problem into the analysis since treatments are no longer orthogonal to the blocks. i.e., every treatment does not occur in every block, resulting in unequal block sizes and unequal replications of treatments. Since this problem first arose in agricultural experiments, where experimental units are called plots, this is referred as missing plot analysis in the literature. There are two approaches to the problem of missing observations. The first is an approximate analysis in which the missing observation is estimated first and the usual analysis of variance is performed proceeding as if the estimated observation were real data, with the error degrees of freedom reducing by one for each missing observation. Second approach is the exact analysis where the data is analyzed as it is as an incomplete block experiment; this analysis involves messy calculations and is less convenient than approximate analysis [1].

Missing data are a problem, especially in large epidemiological studies or in longitudinal studies on chronic illnesses or in public health research relying on routinely collected data. It is often not possible to ensure completeness or plausibility of every item of data, for reasons of time and resources in these situations. Data are likely to be missing if they are related to sensitive issues for e.g., alcoholism, obesity or to intrusive examinations, or if a composite measure is calculated from several variables, each of them affected by missing values [2].

The problem of missing data is not taken as serious by researchers because they do not understand the implications of the missing data on the final result. Cases with missing values those are systematically different from cases without missing values can obscure the results. Also, missing data could produce biased treatment comparisons and may reduce the precision of calculated statistics because there is less information than originally planned. Another concern is that the assumptions behind many statistical procedures are based on complete cases, and missing values can complicate the theory required. Missing value analysis helps address several concerns caused by incomplete data.

It has been generally observed that many researchers are apprehensive as well as unaware about imputation techniques. This paper is an attempt to introduce the basics of imputation and to encourage the researchers to adopt them while facing the problem of missing data. The present paper briefly describes missing data mechanisms, different imputation techniques and examines different imputation techniques to fill in the missing values of the outcome variable in a prospective study.

Missing data mechanisms

Every imputation technique depends on assumptions regarding the missing data mechanism. There are three types of missing data mechanisms.

Missing completely at random (MCAR): MCAR means that 'missingness' is unrelated to the values of any variables, whether missing or observed. Data that are missing because a researcher dropped the test tubes or a participant accidentally skipped questions are likely to be MCAR. Under this mechanism, the observed values come from a random subsample of the total values. The MCAR assumption is the most stringent of the missing data mechanisms, and can be checked using Little's multivariate test for MCAR.

Missing at random (MAR): This means that 'missingness' depends on the observed values but not on missing. In this case the probability of missing data on a particular variable W can depend on other observed variables but not on W itself. For example, missing income data may be unrelated to the actual income values, but are related to education, that educated people are less likely to reveal their income than less educated. This cannot be checked from sample values. MCAR and MAR are known as ignorable mechanisms.

Missing not at random (MNAR): MNAR means that 'missingness' depends on both the observed and missing values. For example, if individuals with higher incomes are less likely to reveal them on a survey than are individuals with lower incomes, the missing data mechanism for income is non-ignorable. Whether income is missing or observed is related to its value. This MNAR mechanism is also known as informative, non- ignorable mechanism. Imputation methods, including multiple imputation, rely on the assumption that data are missing at random (MAR) [3].

Different imputation techniques

There are several methods to handle missing observations. Some of them are explained briefly here.

Complete-case analysis: Is the simplest and the most common way to handle incomplete cases i.e., only cases with complete data will be included. It is default in most statistical packages. However, if the number of variables is large relative to number of cases then even a small number of missing items on each variable can result in large number of incomplete cases [4].

Removing incomplete cases: Is so much easier than imputation and is the first thing anyone would like to do when faced with missing observations. Removing incomplete cases would be a reasonable approach if the discarded cases form a representative and relatively small portion of the entire dataset. However, if the discarded cases differ systematically from the rest estimates may be seriously biased [5]. Removing incomplete case means that subjects with missing value are completely excluded from analysis, while in complete case analysis, only the missing value of a variable gets excluded, the subject remains in the analysis, and his other variables which are complete, are used in the study

Last observation carried forward: Is an extrapolation of the last observed measurement, and could be applied to both continuous as well as discrete variables. This is subjected to bias, especially if 'missingness' and measurement processes are related.

Single-value imputation: Was once the most common imputation method. All the missing values are replaced by a single value for e.g., mean or median. Most commonly single value is mean; hence this method is also known as mean substitution. Single-value imputation is seen as a poor alternative to other imputation methods, because this method sets more density on a single value and therefore changes the form of the distribution. Besides it reduces the variance of the variable and its correlation with other variables. The technique has the advantage of being simple to implement for any type of variable. Also, once the missing values are imputed, multiple users can use the data with consistent results.

Hot deck imputation: This is another example of single value imputation technique. This method searches for other respondents that have the same response patterns over a set of matching variables. Matching variables are variables that are related to or predictive for the variables for which missing values are to be imputed. If a matching respondent is found for a non-respondent, the respondent's value is donated to the nonrespondent, i.e., missing values of non-respondents are replaced by the value of the matching respondent. This technique does not require distributional assumptions. In a way this is seen as an improvement on the mean imputation, as this method creates more variability in the imputed values [3,6].

Regression imputation: Uses auxiliary information on variables that are assumed to be related to the variable containing missing values. An Ordinary Least Square regression model is fitted, and missing values are predicted from the model. Because predicted values usually have a lower variance than observed values, a random error term from the distribution of observed residual values is added. This technique requires the same assumptions as Ordinary Least Square regression and hence is suitable for continuous variables.

Expectation Maximization (EM) imputation: Like regression imputation, this imputation technique is suitable for continuous variables. The EM algorithm consists of two steps- expectation and maximization - and is an iterative algorithm for maximum likelihood estimation. The algorithm calculates conditional expectations of missing data on the basis of observed data. It is then used to calculate maximum likelihood on the expected likelihood to re-estimate the parameters. These reestimated parameters are then used to determine expectations of missing values in a second iteration. The algorithm proceeds until 'convergence' [6]. The theory of the EM algorithm for imputation of missing values is described elsewhere [7]. Regression and EM estimation depend on the assumption that the pattern of 'missingness' is related to the observed values only. This condition is called missing at random, or MAR. This assumption allows estimates to be adjusted using available information.

Multiple imputation (MI): Multiple imputation can be applied to missing observations which are continuous or discrete. It is an area of statistics, which has developed much since the 1980s. It is a Monte Carlo technique in which the missing values are replaced by m >1 simulated versions, where m is typically small (usually 3-10). Application of multiple imputation technique requires three steps: imputation, analysis and pooling.

(i) Imputation - Fill in the missing entries of the incomplete data sets, not once, but m times.

Imputed values are drawn for a distribution. This step results is m complete data sets.

(ii) Analysis - Analyze each of the m completed data sets. This step results in m analyses.

(iii) Pooling - Integrate the m analysis results into a final result. Simple rules exist for combining the m analyses [5]. Figure 1 illustrates these three steps.

Proper use of multiple imputation requires three things: Imposing a probability model on the complete data, specifying a prior distribution for the parameters of the imputation model, and assuming an ignorable missing mechanism (MCAR / MAR) [6]. Efficiency of an estimate based on m imputations is approximately (1+g/m)-1 where g is the rate of missing information for the quantity being estimated. In this light it has been shown that the efficiency of data imputation using multiple imputation is high even when the number of imputed datasets is low (in the 3to10 range). Tests also suggest that multiple imputation is quite robust even when the simulation is based on an erroneous model (for e.g., when normality is assumed for purposes of simulation when the underlying data are not in fact normal [5].

Comparison of imputation techniques

Imputation is an attractive approach to analyzing incomplete data. However, unprincipled imputation method may create more problems than it solves. With the advent of new software the technique of imputation has become increasingly attractive for researchers in the biomedical, behavioral and social sciences, whose investigations are hindered by missing data. Also, there are a number of imputation techniques. An indicator that is often used for comparison of different imputation methods is the Pearson correlation coefficient; though it is not appropriate when the question is about agreement because it tests whether two methods are linearly related. Obviously they must be related as they intend to measure the same [8]. Hence, Altman and Bland suggested comparison of methods based on the differences between individual values of the methods. Mean of the difference is indicative of the relative bias between the two methods. The relative bias can also be tested using a paired t-test [9].

Methods

The present paper attempts to compare different imputation techniques-single value imputation, EM imputation, regression imputation and multiple imputation. The data for the present investigation came from a prospective study designed to find out the predictors of early response to treatment in drug-naive Schizophrenia patients. Seventy-six never-treated patients who met Diagnostic and Statistical Manual-IV (DSM-IV) criteria [10] for schizophrenia and consented to be followed up for 6 weeks were included in the study. All the patients were treated under one clinical unit and received a standard dose of atypical neuroleptic for 6 weeks. The aim of the study was to assess the early response to treatment, and the total scores obtained on Positive and Negative Symptom rating Scale (PANSS) scale was the outcome of the study, and it was assessed every week. PANSS is a 30-item, 7-points rating instrument to evaluate positive, negative and other symptoms dimensions on the basis of a formal semi structured clinical interview and other information sources, and it takes about 45-50 minutes to administer [11]. In many instances it has been noticed that depending on the severity of the illness patient does not co-operate for the assessments to be carried out; or for some other reasons they might not come back for the scheduled weekly follow-ups. Baseline and first follow up (2^nd week) data were complete. PANSS scores were missing from 3^rd week and it was noticed that only 52 patients (68 %) had the PANSS scores at the final assessment at sixth week. Missing values were imputed at all these assessments.

Statistics

Paired t-test and analysis of variance were employed for the comparison of imputation techniques. Software used in the investigation was SPSS (11.0), STATA (7.0) and NORM. Imputations in SPSS can be based on either EM algorithm or regression while STATA uses best subset regression approach. NORM is a free software package for multiple imputation in S-Plus for continuous data. The level of significance was fixed at 0.05.

Results

It can be seen that that about 32% of the patients did not have the outcome, i.e., total PANSS score at sixth week assessment (Table 1). PANSS scores at the baseline and socio demographic variables age, gender, marital status, education, socio-economic status, place of residence and family history were compared between those who have the sixth week PANSS scores and those who do not have. It is found that none of these variables differed significantly between complete cases and cases with missing values.

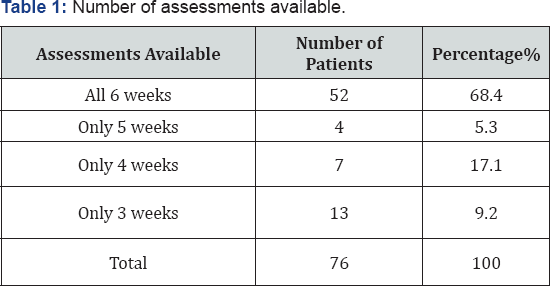
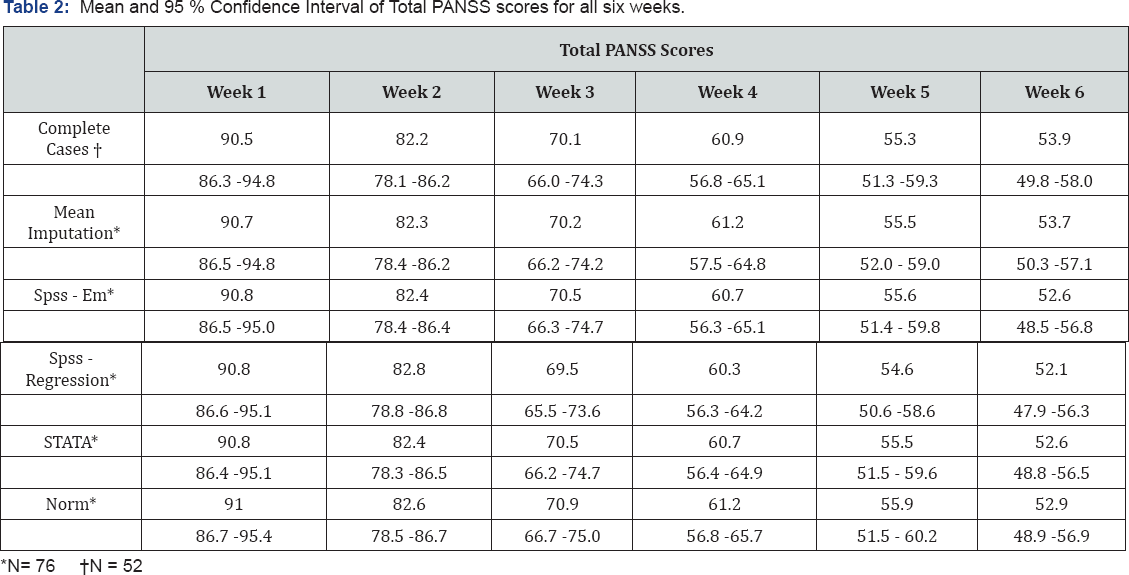
Mean and the 95% confidence interval for the total PANSS score, obtained by various imputation techniques is given in Table 2, for all the six weeks. Careful examination of the table shows that mean imputation has resulted narrower confidence intervals compared to complete cases, this is to be expected because mean imputation reduces the variance of the variable; and imputation using NORM has resulted in wider confidence intervals compared to complete cases (Table 2).

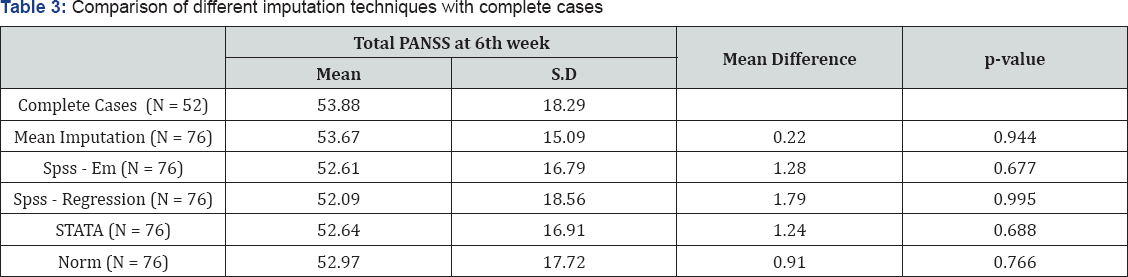
For subsequent analyses, the total PANSS score obtained at sixth assessment alone was considered. Analysis of variance was carried out to see if there is any significant difference between the complete cases and the values obtained by various imputation techniques. Table 3 shows that none of the five techniques resulted in values that were significantly different from those of the complete cases. Regression imputation gave the largest difference between complete and imputed cases (Table 3).

Paired t-tests of total PANSS score at 6th week of various imputation techniques revealed no significant relative biases, but relative bias between the mean imputation and EM imputation was comparable to that between mean imputation and imputation by STATA (Table 4).

PANSS scores at sixth week were deleted for a proportion of complete cases (25%, 50% and 75%), selected at random and the missing value analyses were carried out to examine the efficiency of the imputation techniques. The results were then compared with the complete cases, using analysis of variance. Results of post-hoc analysis showed that imputed values significantly differed from the complete cases only when the rate of missing observation was very high i.e., 0.75 (Table 5). Hence it can be concluded that these imputation techniques are efficient unless the rate of missing observation is not very high.

Conclusion

It is seen that the efficiency of the imputation techniques depends on the rate of 'missingness'. The results of this comparison did not show clear differences between the values of complete cases and the imputed values obtained by various imputation techniques. EM imputation using SPSS resembled imputation using the software STATA, and they resulted in means closer to those of complete cases

References

1. Montgomery DC (1976) Design & Analysis of experiments. John Wiley & sons, New York, USA.
2. Mishra G, Dobson A (2004) Multiple Imputation for body mass index: Lessons from the Australian Longitudinal study on Women's Health. Stat Med 23(19): 3077-3087.
3. Perez A, Dennis RJ, Gil JFA, Rondon MA, Lopez A (2002) Use of the mean, hot deck and multiple imputation techniques to predict outcome in intensive care unit patients in Colombia. Stat Med 21(24): 3885-3896.
4. Song J, Belin TR (2004) Imputation for incomplete high dimensional multivariate normal data using a common factor model. Stat Med 23(18): 2827-2843.
5. Schafer JL (1999) Multiple imputation: A primer. Stat Methods Med Res 8(1): 3-15.
6. Gmel G (2001) Imputation of missing values in the case of a multiple instrument measuring alcohol consumption. Stat Med 20(15): 23692381.
7. Little RJA, Rubin DB (1987) Statistical Analysis with Missing Data. John Wiley & Sons, New York, USA.
8. Bland JM, Altman DG (1986) Statistical methods for assessing agreement between two methods of clinical measurement. The Lancet 327(8476): 307-310.
9. Altman DG, Bland JM (1983) Measurement in medicine: the analysis of method comparison studies. The Statistician 32(3): 307-317.
10. American Psychiatric Association (1994) Diagnostic and Statistical Manual of Mental Disorders. (4^th edn), American Psychiatric Press, Washington DC, USA.
11. Kay SR, Fisbein S, Opler LA (1987) The Positive and Negative syndrome scale (PANSS) for Schizophrenia. Schizophr Bull 13(2): 261-276.