IJESNR Home
Does Renewable Electricity Generation have Zero Marginal Cost?
Thomas Weyman-Jones*
School of Business and Economics, Loughborough University, UK
Submission: December 19, 2022; Published: December 23, 2022
*Corresponding author: Thomas Weyman-Jones, School of Business and Economics, Loughborough University, UK
How to cite this article: Weyman-Jones T G. Does Renewable Electricity Generation have Zero Marginal Cost?. Int J Environ Sci Nat Res. 2022; 31(4): 556318. DOI 10.19080/IJESNR.2022.31.556318
Keywords: Electricity generation systems; Renewable system; Marginal cost; Technologies; Carbon taxes; Wind power
Opinion
Should the price of wind power be decoupled from nonrenewables?
A marked feature of the surge in world energy prices has been suggestions to decouple marginal pricing in electricity generation systems that use renewable generation such as wind power from the world price of gas. For example, the UK Government issued a consultation study on reviewing electricity market arrangements that included questions about moving away from marginal pricing and splitting the wholesale market, so that some renewables receive an average price, independent of the marginal cost of production, see UK Government [1]. The argument was that the marginal pricing model may become less desirable in the transition to a majority renewable system, since the cost structure of renewables means that most of their system costs will be in construction rather than in operation. The implication is that since renewable generation may have close to zero operating cost, it therefore has zero short run marginal cost so that the marginal pricing approach becomes redundant. This note shows that the argument is erroneous and that zero operating cost does not mean zero short run marginal cost nor does it indicate the redundancy of marginal pricing.
The essential objective of the decoupling argument is to maximize the penetration of renewable technologies such as wind power into the generating system. The first issue to note is that separating the electricity market into renewable and nonrenewable segments with different prices on the basis of cost differences invites market participants to arbitrage between them to erode the difference in prices. In doing so, the participants expend scarce resources in evading artificial differences between the two markets. In fact, an efficient mechanism for increasing the relative share of renewables already exists in the form of carbon pricing using carbon taxes or tradable permits.
The major point is that the negligible or zero operating cost of renewables such as wind power generation does not mean that they have zero short run marginal cost and does not undermine the efficiency case for marginal pricing. This is because the argument fails to understand that marginal cost is not a measure of cost associated with each different type of capacity but is a measure of the strength of demand. For this reason, marginal cost is a system calculation and is unique to the whole generating system at a point in time. Short run marginal cost is the price that rations demand to capacity. These points can be illustrated in a simple model.
Model
There are two types of capacity: type 1 is renewable with operating cost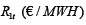 
per period and construction cost 
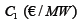; type 2 is nonrenewable with corresponding 
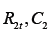. The output per period from each type is 
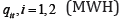and the capacity installed of each type is 
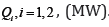. Demand per period is 
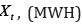. There is a discount factor applied to cash flows: 
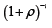so that the present values of the operating costs
are: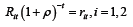 
and ρ is the discount rate. I assume that both plant types have the same operating life, but if this is not the case the difference is easily handled by using equivalent annuity factors. The system cost present value minimization problem is:
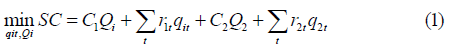
Subject to the constraints that output from each type cannot exceed capacity in any period, and the total output from both capacity types must at least meet the total system demand in each period:
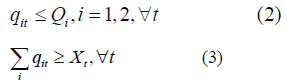
At an optimum the efficiency conditions with Kuhn-Tucker
multipliers (shadow prices)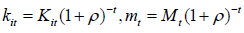 
is are:
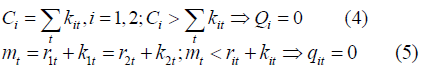
The first efficiency condition requires that the present value
of the capacity payments (€/MW) for each type of capacity covers
its construction cost; if not the capacity is not used. The second
requires that the system marginal price or short run marginal
cost in each period,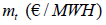 
equals the sum of the operating cost and the capacity payment on each type of capacity; if not
then the output is not used. This second efficiency condition
holds independently of whether the operating cost of type 1 is
zero or not, because the system marginal price is, by the envelope
theorem, equal to:
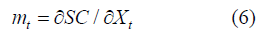
In other words, it measures the effect on the present value of system cost of increases or decreases in the pressure of system demand. If the operating cost of type 1 capacity, e.g., wind generation is zero, the system marginal price simply covers its required present value capacity payment factor. Zero operating cost has no effect on system marginal price or short run marginal cost because system marginal price is not measured as a cost but as a signal of demand pressure. Imagine that the type 2, e.g., gas fired generation, operating cost escalated steeply. The system marginal price would signal the need to install more wind generation because the capacity payment factor to wind power would rise in proportion. It would not signal the opportunity to reduce the price of electricity by charging a close to zero price for wind generation. Therefore, decoupling the price of wind generation from the price of gas generation as given by system marginal price would be a seriously inefficient error. What about the converse argument: can marginal cost equal zero in a system with positive operating costs? The answer is yes. Among the Kuhn- Tucker complementary slackness conditions is:
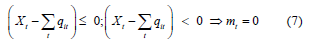
If the available output from all generating capacity in a given
period exceeds the market demand, then short run marginal cost,
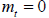. In this event the efficient response is to scrap capacity and since the last capacity to be scrapped will always be that with the
lowest or zero operating cost, such an outcome would increase
the relative share of renewables or wind generation in the system.
In summary: zero operating cost for wind generation does not
mean that short run marginal cost is zero; conversely, zero system
marginal cost will increase the share of wind generation in the
system in the event of a rise in the price of gas. In the long run
with a fully optimized system, long run and short run marginal
cost are equal.
Issues of intermittency, capacity safety margin and stochastic
demand have not been addressed because they do not alter the
main point which is that capacity operating cost is not marginal
cost and marginal cost is unique to the total system not to capacity
types. In practice new wind capacity is often arranged through a
fixed price contract to cover the construction cost over the life
of the project. However, that fixed price construction cost must
be efficiently allocated to each period of demand. A convenient
approximation rule for doing this is to use the levelized discounted
cost of the capacity, adjusted for its average yearly load factor
expressed in MWH. Disaggregate the yearly loads for each capacity
type by hours of the year: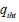 
; then, if 
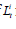is the projected load factor of each type of capacity in each year on the system cost simulation and H is the number of hours in the year,
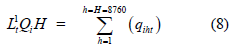
So that for wind generation with zero operating cost, the levelized discounted cost (€/MWH) is:
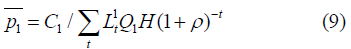
Then this value may be used to represent the contribution to system marginal cost in each hour and year of wind generation with zero operating cost under a fixed price contract..
