Research article

Effect of Various Kinds of Stilling Basin’s Baffle Blocks Arrangement on River Bed Scour

Mohamed Abdelkader¹*, Cahit Yerdelen² and Muhammet Yaman²

¹ Department of Civil, Environmental, and Ocean Engineering (CEOE), Stevens Institute of Technology, USA

² Department of Civil Engineering, Engineering Faculty, Ege University, Turkey

Submission: June 14, 2022; Published: June 24, 2022

*Corresponding author: Mohamed Abdelkader, Department of Civil, Environmental, and Ocean Engineering (CEOE), Stevens Institute of Technology, Hoboken, NJ, USA

How to cite this article: Mohamed A, Cahit Y, Muhammet Y. Effect of Various Kinds of Stilling Basin’s Baffle Blocks Arrangement on River Bed Scour. Int J Environ Sci Nat Res. 2022; 30(4): 556295. DOI: 10.19080/IJESNR.2022.30.556295

Abstract

The management of water retaining structures and their environmental impacts are critical aspects of hydraulic engineering studies. From an environmental perspective, hydraulic structure planning is primarily concerned with the design of the water-releasing sections (outlet) of the water retaining structures. It is essential that such structures are properly designed in order to meet the requirements of sustainability of the surrounding ecological system. This study aims to examine the impact of hydraulic jump stilling basin length and energy dissipation blocks on scour depth and reach an optimum performance of the stilling basin. To this end, an experimental study was conducted to investigate the effect of the stilling basin's baffle blocks on the river bed scour downstream of a water-retaining structure. Several hydraulic parameters were incorporated in the analysis and design of the stilling basin. The study introduces a novel approach to estimating the maximum scour based on a non-linear regression model.

Keywords: Open channel; Stilling basin; Baffle block; Maximum scour depth

Introduction

Water retaining structures can be built for a variety of purposes, including irrigation, the supply of potable and industrial water, hydropower, flood control, recreation, river and inland waterway transport, desalination at river deltas, sediment retention, control and improvement of the quality of water, collection of waste, and protection of the ecosystem [1]. However, the efficiency of a water structure design is crucial for the sustainability of the surrounding ecosystem.

A water-retaining structure will generally result in an increase in water depth upstream of the structure. Therefore, there will be a significant difference between the potential energy at the upstream and downstream of the structure. Potential energy retained in the upstream section is converted into high amounts of kinetic energy in the downstream section. Fluid with high kinetic energy causes degradation in the river bed by increasing the irregularity and vector size of streamlines. Degradation can be described as sediment transportation caused by the kinetic energy of water in the natural river bed. Hydraulic structures should be modified to manage and dissipate the kinetic energy of water, which leads to degradation. Structures such as stilling basins, stepped spillways, and impact walls are examples of energy dissipators. In our study, we used energy dissipators that consisted of a stilling basin and blocks within the basin.

Stilling basins are an integral part of weirs, spillways, and dams. In order to protect the bed and banks from excessive scouring, it is necessary to reduce the kinetic energy of incoming water to a permissible level. This is done before releasing it into a channel downstream. The design of stilling basins and energy dissipators has been addressed in several studies [2-6]. The development of cutting-edge technologies and materials, computer software, and the expansion of the number of features of measuring devices are the basis for the continuation of studies on the design of stilling basins and energy dissipators. Researchers in the field of hydraulic engineering have conducted many experiments regarding the management and diversion of the energy released during the transmission of water stored in water retaining structures. The main objectives of the referred experiments are to improve the design of the most common stilling basin types and to obtain a more efficient and economical design.

In particular, the work carried out by Verma and Goel between 1999 and 2006 is noteworthy; The effects of different elements and their arrangement on the bed scour in the energizing zone of the water structure with a circular cross-sectional outlet were extensively studied and a dimensionless size called the "scour index" was used to make comparisons [7-10]. Tiwari [11] also designed a circular section post-exit calming pool in his study, but he evaluated it by incorporating a different set of parameters than Verma and Goel. Tiwari and Goel investigated the "impact wall" effect in a circular outlet water structure [12]. Ali [13] changed the roughness of the bed by using cube-shaped baffle blocks [13]. He then investigated the effect of changes in bed roughness on hydraulic jump length. The results obtained indicated that the length of the hydraulic jump had decreased due to the change in bed roughness. Ellayn & Sun [14] examined hydraulic jump stilling basins with wedge-shaped and pentagonal baffle blocks. In a comparison of the results of experiments performed with and without baffle blocks, the researchers concluded that the baffle blocks helped to shorten the length of the stilling basin [14]. Bestawy [15] focused on a sediment basin containing uniform sediment, and baffle blocks with different geometrical and dimensional characteristics. According to the results of the study, the semi-circular and trapezoidal baffle blocks have provided the best results [15]. Al-Mansori et al. [16] The authors presented only the results of their study on Energy Dissipation of the geometric properties of baffle blocks [16]. Alternatively, Elsaeed et al. [17] studied experimentally the effect of the water jet designed for the drop bearing on scour, and recommended designs that caused less scour to be used [17]. In addition to experimental and field studies, some of which have been mentioned, there are also studies that have been conducted by simulating the process in a computer environment. Aydın et al. [18] observed the standard discharge channel and the discharge channel containing baffle blocks using the Flow-3D program. The study used three different discharge values, as well as one type of baffle block, which was placed transversely on the bottom of the channel. In the study of Macián-Pérez et al. [19] the stilling basin’s physical and numerical modeling performances had been evaluated. Additionally, the study aimed to characterize the hydraulic jump in the stilling basin by studying a small-scale model, as well as Computational Fluid Dynamics (CFD) model [19].

The purpose of this study is to investigate the relationship between the design parameters of stilling basins, the energy ratio, and the maximum scour depth, and to suggest optimum design features that control the river bed degradation. The Experimental study is conducted in order to determine the criteria for minimizing changes in natural streambeds by utilizing measurable parameters. In order to achieve this objective, it was investigated how the design parameters such as water head, flow velocity, size of baffle block, arrangement of baffle block, and length of stilling basin affect the energy of the fluid, sediment transportation, and scour depth at stilling basins that contain prismatic shaped baffle blocks. Thus, the study presents a novel empirical approach to estimate the optimum design features of the stilling basin with higher performance

Experimental Setup

Several variables are used in studies of scour depth in the riverbed [4,11,16,20,21]. The scour depth depends on a large number of flow and basin variables (geometric, kinematic, and dynamic variables) as follows.

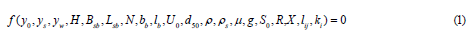
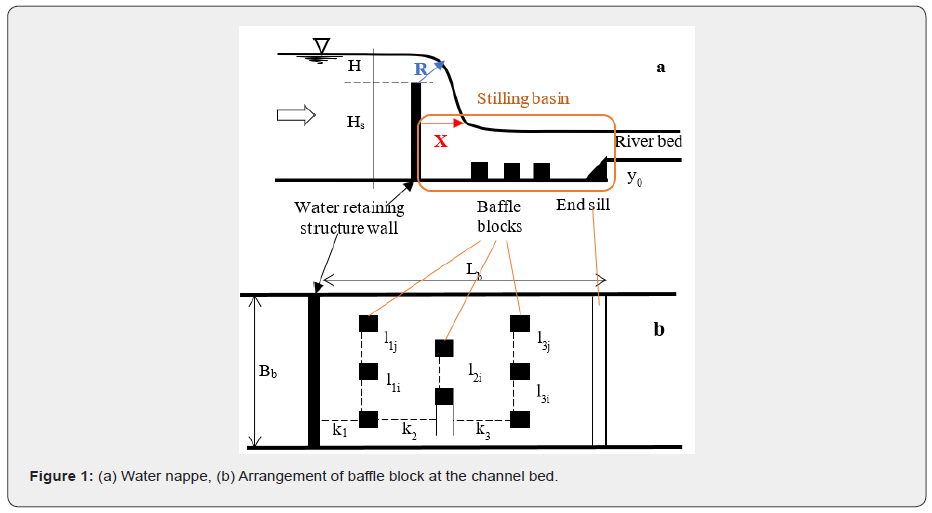
in which y_o: initial sediment/soil layer thickness, y_s: maximum scour depth, y_w; water depth, H; water head, B_sb; stilling basin width, L_sb; stilling basin length, N; number of baffles , h_b; baffles height, b_b; baffles width, U₀; flow velocity, ρ; density of the water, d_50; mean size of bed material, ρ; density of the water, ρs; density of bed material, and μ; dynamic viscosity of water, g; gravitational acceleration, S₀; bed slope of the channel, R: the radius of water nappe, X: the length of water nappe l_ij: the distance between the baffle blocks, k_i: the distance between the rows of baffle blocks.

Since d₅₀, ρ, ρ_s, μ, and S₀ were kept constant throughout the experimental program, they removed from Eq. (1). The remaining parameters were made into the following dimensionless quantities with the help of the dimensional analysis method proposed by Langhaar (Eq. 2).

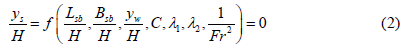
The non-dimensional parameters C, λ₁, and λ₂ were calculated using Equations 3, 4, and 5. The other parameters that were used for the calculation are shown in Figure 1.

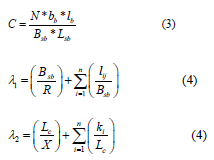
where c: the occupancy rate of the bed of the stilling basin, λ₁: the arrangement coefficient of the baffle blocks, λ₂: the distance coefficient of the baffle blocks.

The experiments were conducted in the Hydraulic Laboratory of the Civil Engineering Department of Ege University in a channel that can be used to mimic a river environment. The channel is 18 meters long, 0.7 meters wide, and 0.6 meters high. The sidewalls of the channel are made of fiberglass that is 1cm thick. The channel bed was formed by using a smooth silicone filler. The flow was controlled by the pump, which was controlled by the computer and the inverter. The depth of the water and the discharge were measured with an ultrasonic water level meter and a flow meter, respectively, and recorded throughout the experiment. The ultrasonic level meters were used to determine the flow depth in the channel, and the water levels at specific points were measured. Data loggers recorded discharge and flow depth measurements at each second of the experiment for use in developing the regression model.

As shown in Figure 2a, three different sizes of cubic baffle blocks were used in these experiments. In the experiment, the end sill was scaled to 1:1 as shown in Figure 2b. River sand with a uniform gradation distribution curve, which had a material size distribution of d₅₀ = 1.36mm, was used as bed material (Figure 2c & Table 1).

The experiments were carried out using three different water head ratios (water depth/weir height). 90 repetitive tests were carried out in total:

a) without baffle blocks

b) with one row of baffle blocks,

c) with two rows of baffle blocks,

d) with three rows of baffle blocks, and

e) with a stilling basin length of 225 cm,

f) with a stilling basin length of 337.5 cm,

g) with a stilling basin length of 450 cm.

It is important to mention that the experiments were conducted for two hours after each experiment was initiated, and then the flow characteristics were measured. As there is no sediment available for scouring holes, all experiments were conducted in clear water. After the experiment was completed, the flow rate was stopped by shutting down the pump. Gradually, the pump's power was reduced so that the bottom structure was not affected by the flow arrest. In other words, once the scour depth reached equilibrium, the water flow in the channel was gradually reduced and stopped, and the water in the cavities was expected to drain by gravity. The morphology of the bed was then determined by using measurements taken by a digital laser meter with millimeter precision.

Results and Discussion

The effects of various parameters on the maximum scour depth were analyzed graphically and compared with those of previous studies. In order to interpret the effect of these parameters, the maximum scours depth by subdivision was considered.

Effect of water head

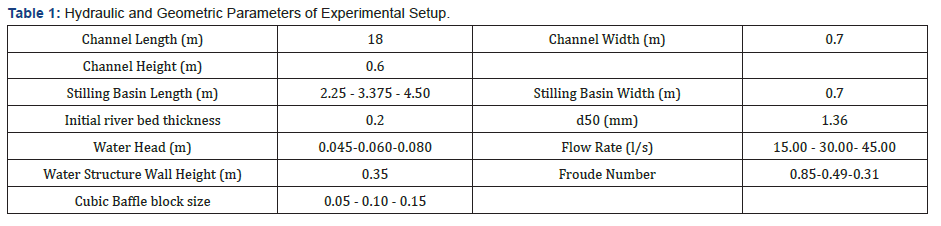
Three different water head ratios (H/Hs) as being 0.129, 0.171, and 0.229 were used during the experiments. Based on the data obtained from the tests, it was found in all the designs that the value of the scour depth ratio is increasing as the water head ratio increases (Figure 3).

The results indicate that when the water head was initially increased approximately by 50%, the scour depth ratio increased approximately by 42% for all the designs. The scour depth ratio increased approximately by 38% for all designs when the water head ratio was increased by 50% again. The water head ratio increased at a constant rate, but the scour depth ratio decreased. These factors should be taken into account during the optimal design process.

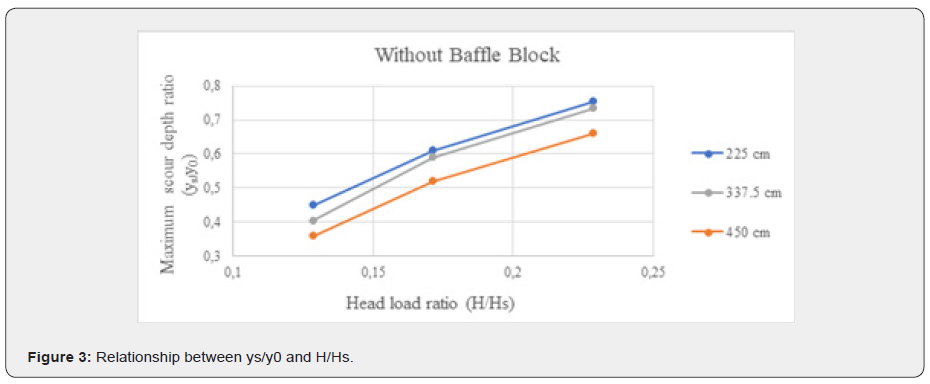
Effect of stilling basin’s length

During the experiments, three different stilling basin length ratios (Lb/Hs) were used: 6.429, 9.643, and 12.857. The results were evaluated based on the maximum scour depth and the points where the maximum scour was observed. According to the experiments performed, the higher the stilling basin length ratio, the lower the maximum scour depth ratio (Figure 4). The maximum scours depth ratio did not change by more than 10% when the stilling basin length ratio was increased by 50%. On the other hand, the lowest maximum scour depth ratio was observed under the highest stilling basin length ratio. Nevertheless, the economic efficiency of a large stilling basin design is less than that of other stilling basin length ratios according to the optimal engineering design concept.

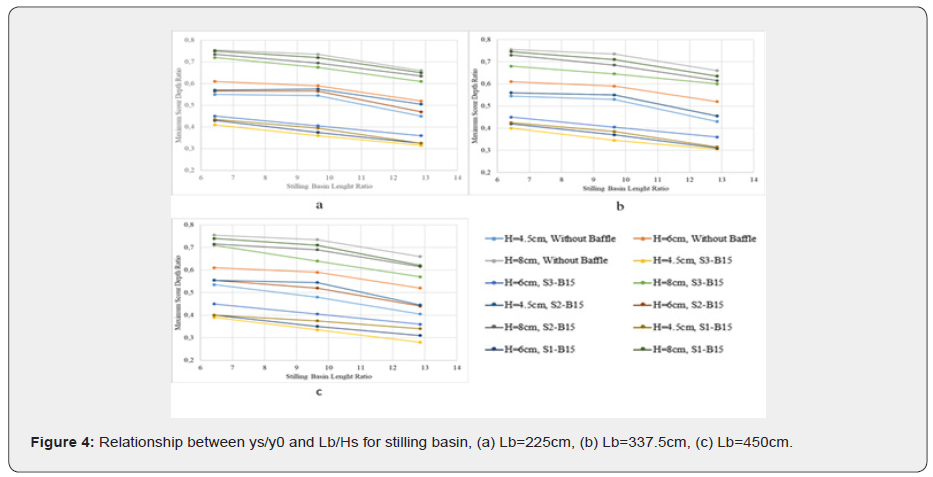
Figure 5 illustrates the channel bed morphologies of designs without baffle blocks. The morphology shown in the figure corresponds to the center of the sediment basin. The maximum scour depths were observed approximately equidistant from the starting point of the natural river bed at the points where maximum scour depths were observed. The maximum scours depth ratio was determined to be 0.755.

Effect of baffle block’s size

The experiments were conducted using stilling basins with three different block size ratios (Hb/Hs = 0.143, 0.286, and 0.429) (Figure 6). Observations from experiments indicate that as the block size ratio increased, the maximum scour depth ratio decreased for the same experimental setups (Figure 7). Comparing the block size ratios for identical system configurations, it was observed that the scour depth decreased by an average of 3%. The same comparison was performed using block size ratios of 0.286 and 0.429, and the scour depth was reduced by 2.5% on average. During prototype model studies, these values must be taken into account in the most critical cross-section design.

Effect of baffle block’s arrangement

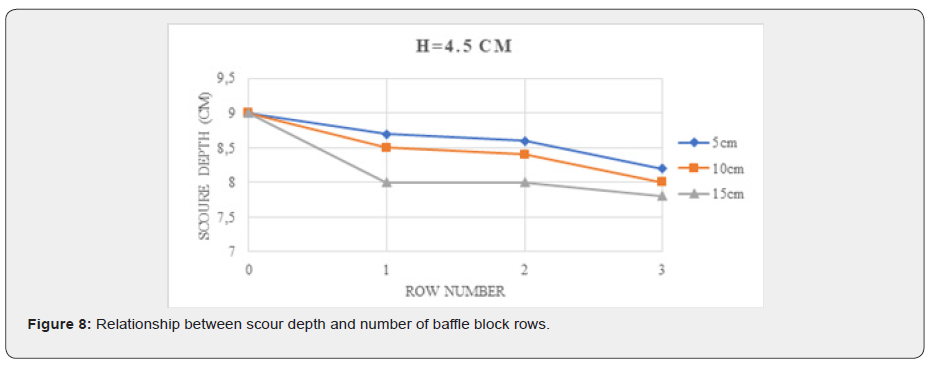
The experiments were conducted with four different arrangements: one row of baffle blocks, two rows of baffle blocks, three rows of baffle blocks, and without baffle blocks (Figure 4). Using the results obtained from the experiments, it was observed that the scour depth decreased as the number of baffle block rows increased (Figure 8).

According to the results, although the length of the stilling basin remained constant, there was no significant difference in the maximum scour depth between experiments performed with one row and two rows of baffle blocks. Furthermore, the maximum scour depth decreased by 10% when compared to experiments performed with one row and three rows of baffle blocks.

Investigation of the maximum scour depth

In order to determine the maximum scour depths, we used a dimensionless analysis, which is commonly used to handle complex physical models. Equation 5 outlines the parameters used in the dimensional analysis.

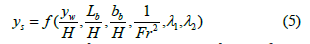
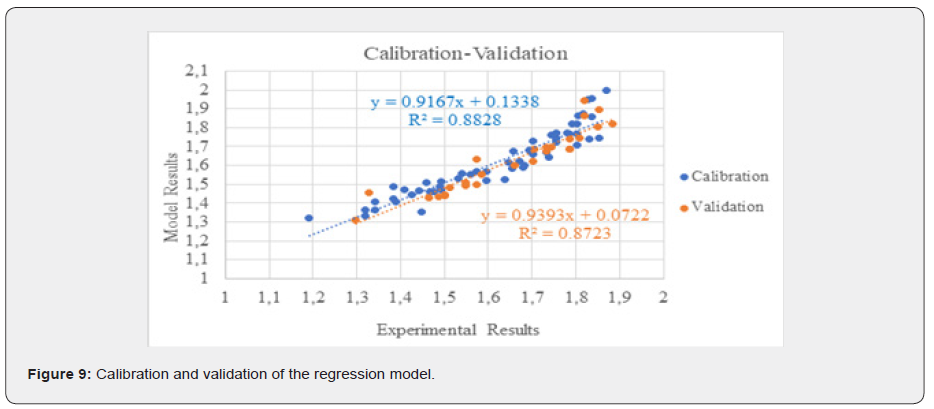
Using the parameters with significant coefficients obtained following the step-wise regression analysis, the scouring estimating model was calibrated and validated. The calibration was performed using 67% of the data set, and the validation was performed using the remaining 33%. Figure 9 illustrates the comparison of calibration and validation results. In Equation 6, we present the parameters affecting the maximum scour depth as a result of nonlinear multiple regression analysis, as well as the validation, where significant coefficients were obtained. Table 2 presents the coefficients of each parameter resulting from the regression analysis.

Based on all the calculations and the graphs obtained, Equation 7 is suggested for the maximum scour depth parameter, which is a non-dimensional parameter.

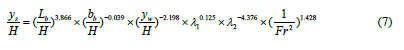
Conclusion

In this study, the relationship between the stilling basin's design parameters (the length of the stilling basin, the size of the baffle block, the arrangement of the baffle block), the energy dissipation rate, and the maximum scour depth was examined. The maximum scour depth decreased by 2% - 15% when the basin length ratio was increased by 50%. Increasing the same parameter to 100% resulted in a decrease of 16% - 29% in the scour depth. The energy of water was measured at different locations during the experiment. The measurement points were located before the water retaining structure, as well as before and after the baffle blocks. When the basin length ratio was at its maximum, the maximum energy change was observed as 39%. When the basin length ratio was the smallest, the minimum energy change was observed to be approximately 30%.

The other parameters investigated were the effect of the baffle blocks and the arrangement of the baffle blocks on the energy ratio and the maximum scour depth. Initially, the stilling basin was not equipped with baffle blocks. This setup was used as a reference for the study. The experiments were conducted for setups containing one row, two rows, and three rows of baffle blocks in the stilling basin.

The results indicated that the energy ratio increased as the block sizes increased, and therefore, the maximum scour depths decreased. According to all the experimental results, the scour depth decreased by about 3%. The designs were examined in terms of arrangement criteria, and no significant differences were observed between the cases of having one row and two rows. In the case of having one row and three rows, the maximum scour depth values decreased by approximately 6%-12%. In the analysis of nonlinear multiple regression, which was conducted using the non-dimensional parameters in the model, it was found that the suggested model estimates 90% of the observed maximum scour depth. It is essential to consider this ratio when developing prototype models or when improving this study.

As a result of the experimental studies, it was observed that the scouring was greater at the edge of the channel bed's width than at the center of the channel bed due to the effect of the sidewall. In order to avoid the effects of the sidewall, future studies may be improved by considering a wider channel. Additionally, this experimental study used 1-2.5mm uniform siliceous river sand in the sediment basins. Thus, experimental sets with different sediment types can be performed to observe the effects of sediment gradation and particle diameter on scouring.

References

1. Ağıralioğlu N (2004) Baraj Planlama ve Tasarımı I. (In Turkish)
2. Peterka AJ (1984) Hydraulic Design of Stilling Basins and Energy Dissipators. A Water Resources Technical Publication, Engineering Monograph No. 95.
3. Bollaert EFR, Lesleighter EJ (2014) Spillway Rock Scour Experience and Analysis - the Australian Scene over the past Four Decades. 5th International Symposium on Hydraulic Structures Brisbane, Australia.
4. Elnikhely EA (2018) Investigation and analysis of scour downstream of a spillway. Ain Shams Engineering Journal 9: 2275-2282
5. Balouchia B, Nikooa MR, AdamowskibaJ (2015) Development of expert systems for the prediction of scour depth under live-bed conditions at river confluences: Application of different types of ANNs and the M5P model tree. Applied Soft Computing 34: 51-59.
6. Amini N, Balouchi B, Bejestan MS (2017) Reduction of local scour at river confluences using a collar. International Journal of Sediment Research 32(3): 364-372.
7. Goel A, Verma DV (1999) Improved design of energy dissipators for pipe outlets. Irrig Drain Syst 13: 313-320.
8. Verma DVS, Goel A (2000) Stilling Basins for Pipe Outlets Using Wedge-Shaped Splitter Block. J Irrig Drain Eng 126(3): 179-184.
9. Verma DVS, Goel A (2003) Development of Efficient Stilling Basins for Pipe Outlets. J Irrig Drain Eng 129(3): 194-200.
10. Goel A, Verma DVS (2006) Alternate designs of stilling basins for pipe outlets. Irrig Drain Syst 20: 139-150.
11. Tiwari HL (2013) Design of Stilling Basin Model with Impact Wall and end Sill. Research Journal of Recent Sciences 2(3): 59-63.
12. Tiwari HL, Goel A (2016) Effect of impact wall on energy dissipation in stilling basin. KSCE J Civ Eng 20: 463-467.
13. Ali M (1991) Effect of Roughened-Bed Stilling Basin on Length of Rectangular Hydraulıc Jump. J Hydraul Eng 117(1): 83-93.
14. Ellayn AF, Sun ZL (2012) Hydraulic jump basins with wedge-shaped baffles. J Zhejiang Univ Sci A 13: 519-525.
15. Bestawy A (2013) New Shapes of Baffle Piers Used in Stilling Basins as Energy Dissipators. Asian Trans Eng 3: 1-7.
16. Al-Mansori NJH, Alfatlawi TJM, Hashim KS, Al-Zubaidi LS (2020) The Effects of Different Shaped Baffle Blocks on the Energy Dissipation. Civil Engineering Journal 6(5): 961-973.
17. Elsaeed G, Ali AM, El-Hazek AN, Ibraheem AMM (2020) Influence of Using Floor Jets on the Local Scour Downstream Fayoum Type Weir. Asian Journal of Engineering and Technology 8(1): 13-22.
18. Aydın MC, Ulu AE (2018) Effects of different shaped baffle blocks on the energy dissipation and the downstream scour of a regulator. Journal of Science and Technology 8(2): 69-74.
19. Macián-Pérez JF, García-Bartual R, Huber B, Bayon A, Vallés-Morán FJ (2020) Analysis of the Flow in a Typified USBR II Stilling Basin through a Numerical and Physical Modeling Approach. Water (Switzerland) 12(1): 227.
20. Balouchi B, Rakhshandehroo G (2018) Using Physical and Soft Computing Models to Evaluate Discharge Coefficient for Combined Weir–Gate Structures Under Free Flow Conditions. Iranian Journal of Science and Technology, Transactions of Civil Engineering 42: 427-438.
21. Langhaar HL (1980) Dimensional Analysis and Theory of Models.